Имитационное аналитическое и статистическое моделирование балансировки гибких роторов турбокомпрессоров

В машиностроении находят широкое применение так называемые гибкие роторы, для которых выполнение условий уравновешенности уже не обеспечивает спокойной работы при минимальном уровне вибраций [1, 2, 4, 6-7]:

r

Таким образом, значения U ‘

r и U" от-

вечают условиям уравновешенности жесткого ротора. Этим, однако, не исключается возможность его прогиба, значение которого в точке крепления диска будет равно[1, 6-7]:

J U ( z)dz + m U k = 0;

lr

J ^U ( ^z X ^z - z c ) dz ⁺ Ё ^Uk ( z k - z c ) = ⁰

где u ( z ) = m ( z ) • r ( z ) — погонный дисбаланс; r ( z ) — смещения центров масс элементов ротора от оси вращения (эксцентриситеты); m ( z ) —

погонная масса ротора, U k – сосредоточенные дисбалансы.

Гибким, согласно ГОСТ 19534-74, называют ротор, который, будучи даже идеально сбалансирован-

ным на частотах вращения, значительно меньших первой критической скорости, на более высоких частотах (вплоть до наибольшей эксплуатационной) имеет динамические реакции и прогибы, недопустимые в условиях нормальной эксплуатации.

Сущность проблем, относящихся к этому случаю, покажем на примере одномассового ротора (рис. 1). Диск имеет радиальное смещение (эксцентриситет) £ относительно осевой линии вала. Соответствующий этому эксцентриситету дисбаланс U = m e скомпенсирован двумя симметрично расположенными корректирующими массами, создающими дисбалансы:

rr

U ' = U " =

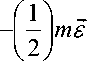
h =

mere2 («11 - «12)

Г

-

re

V re0 7

где ^ 0 = ----- — значение критической ско-

У т а 11

рости; а н и « 12 - статические коэффициенты податливости.

Здесь и в дальнейшем предполагается, что корректирующие массы ничтожно малы по сравнению с массой ротора, так что их влиянием на частоту и форму собственных колебаний пренебрегаем.

_r Итак, _r установка уравновешивающих грузов U ' и U " отнюдь не исключает прогиба вала, который неограниченно возрастает по мере приближения угловой скорости вращения к критической. Значит, выполнения условий (1) недостаточно для уравновешивания гибкого вала. Его уравновешенность будет достигнута только при том дополнительном условии, что ан = ^ 12 . Но

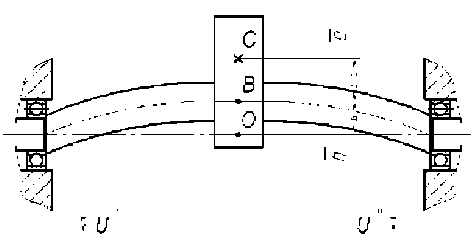
Рис. 1. Схема одномассового ротора

это означает, что для гибкого ротора корректирующие массы должны устанавливаться именно в той плоскости, где сосредоточен дисбаланс. Следовательно, условием полной уравновешенности гибкого ротора является уравновешенность каждого его элемента, образованного двумя бесконечно близкими поперечными сечениями. Если учесть, что закон изменения дисбаланса по длине ротора в общем случае неизвестен, то станет ясно, почему эта простая, на первый взгляд, задача принимает характер достаточно сложной научно-технической проблемы.

В случае жесткого ротора считаются применимыми известные в механике определения абсолютно твердого тела и соответствующие условия уравновешенности. Эти условия могут быть выполнены с помощью двух корректирующих масс, располагаемых в различных плоскостях коррекции, причем уравновешенность, достигнутая на одной какой-либо частоте вращения, не будет нарушена и на любой другой.

Более сложной является задача уравновешивания гибких роторов, подверженных заметным изгибным деформациям [1, 2, 4, 6-7]. В этом случае указанных выше условий недостаточно для обеспечения допустимого уровня вибраций. Полная уравновешенность гибкого ротора означает устранение внутренних изгибающих моментов от неуравновешенных центробежных сил во всех его сечениях. Но поскольку истинное распределение дисбаланса, как отмечалось, неизвестно, а число плоскостей коррекции весьма ограничено, то такая задача принципиально невыполнима. Речь может идти только о некотором частичном уравновешивании, удовлетворяющем требованиям эксплуатации.

Основные положения, в соответствии с которыми балансируются гибкие роторы, сводятся к следующему [1, 2, 4, 6-7].

Критерием гибкости ротора служит отношение максимальной рабочей частоты вращения к первой критической частоте п * ротора, установленного на абсолютно жестких (в радиальных направлениях) опорах. Если это отношение не превышает 0,5, ротор относится к категории жестких, в противном случае – к категории гибких.

Наиболее эффективными являются такие методы балансировки, в которых комбинируются условия статического равновесия и некоторые динамические условия. Таковыми могут быть: устранение определенного числа собственных форм изгибных колебаний из кривой динамического прогиба; устранение прогибов на заданных частотах и в заданных точках; устранение динамических реакций подшипников на заданных частотах и др. С точки зрения эффективности балансировки все они примерно равноценны, а чис- ло потребных плоскостей коррекции на 2 превышает количество выбранных динамических условий. Для ротора, работающего в диапазоне 0 < п < 4,5п* , чаще всего достаточно четырех плоскостей; в диапазоне 0 < п < 3п* число плоскостей коррекции можно уменьшить до трех.

Влияние упругодемпфирующих характеристик опор на качество балансировки сравнительно невелико [1]. Если какой-либо метод балансировки достаточно эффективен для ротора на жестких опорах, он сохраняет свою относительную эффективность при переходе на упругоподатливые или упругодемпфирующие опоры.

Наибольшая сложность при балансировке гибких роторов связана с потребностью в высокочастотных балансировочных стендах, оснащенных современной виброизмерительной аппаратурой и вычислительной техникой. Только в этом случае могут быть замерены динамические реакции или прогибы, определены балансировочные коэффициенты и выполнены соответствующие условия балансировки. Эффективность же известных способов низкочастотной балансировки носит статистический характер и не может служить гарантией надежной безвибрационной работы каждого отдельного изделия. Но здесь важ- ное исключение составляют роторы, распределение дисбалансов которых может быть найдено по результатам измерений на низкочастотных балансировочных станках. К ним, в частности, относят- ся роторы, выполненные в виде центрального вала, несущего на себе ряд дисков.

В работах [1, 4, 9] предложена технология низкочастотной балансировки гибких роторов компрессорных агрегатов “Синтезгаз”, включа- ющая следующие операции.

rr

• 1.    Измерение дисбалансов A_o и B_o , центрального вала в плоскостях опорных подшипников;

• 2.    Сборка первого промежуточного узла, включающего вал и один из дисков _r , и измерение в тех же плоскостях дисбалансов A 1 и B 1 ;

• 3.    Операция 2 последовательно повторяется для второго узла, включающего два диска, затем для третьего, четвертого, и, наконец, последнего n-го узла, представляющего уже окончательно

собранный ротор;

r

• _r 4. По результатам измерения дисбалансов A_k и B_k (k=0…n) последовательно определяются:

• а)    проекции дисбалансов А_ky , А_kz и B_ky , B_kz на координатные плоскости YX и ZX, жестко связанные с ротором (ось Х направлена по оси вращения);

• б)    проекции статических и моментных дисбалансов самих дисков:

U ky =A A ky +^ B ky ;   U kz =A A kz ₊^ B kz ;

V. =^A,yхk -^Bky(l -xk); Vky =A4kzXk -^BkZ(l -xk), где ДАky = Aky - Ak-iy; ABky = B. - Bk-1,y ; ДАkz = Akz - Ak-1,z; ДBkz = Bkz - Bk-1,z; k — номер балансируемого узла; хk – расстояние от левой опоры до центра масс k-го диска. Таким образом, функция распределения дисбалансов становится полностью определенной.

• в)    назначаются плоскости коррекции дисбалансов. Примем, что это плоскости х₁ , х 4 , х ₇ , х ₈ , проходящие через центры масс соответствующих дисков.

• г)    назначаются плоскости, в которых согласно условиям балансировки должны быть устранены динамические прогибы на заданной угловой скорости вращения. Пусть координаты этих плоскостей х 4 , х ₇ .

• д)    определяются проекции дисбалансов корректирующих масс D_{1 y} , D _{4 y} , D _{7 y} , D _{8 y} из системы уравнений:

N + 2 r      r r

Z Dk = -(A + B);

k = 1

N + 2 r       r

Z D k X k =- B • l ; [ k = 1

N + 2 r

Z Da. =-г0, k =1

где N – число динамических условий выполняемых при уравновешивании; Ar и Br – дисбалансы ротора, измеряемые на его опорах; l – рассто- яние между опорами; a ik - динамические коэффициенты податливости; i=1, 2_N; ri о — прогибы в некоторых точках x = x^, вызываемые начальным дисбалансом и подлежащие устранению посредством балансировки.

• е)    определяются проекции дисбалансов корректирующих масс D _{1 z}, D _{4 z}, D _{7 z}, D 8 _z из системы уравнений, аналогичной системе (2), но записанной для плоскости ZX.

• ж)    определяются модули и углы дисбалан-

• сов корректирующих масс:

D

• D , = JD 2 + D iz ; ^ - = ^arccos^ .

• 5.    Выполняется коррекция дисбаланса и контроль качества балансировки: при правильно выполненном расчете и точной коррекции величины остаточных дисбалансов, замеренные на

где i = 1, 4, 7, 8 – номера плоскостей коррекции;

опорах ротора, не должны превышать установленные допуски.

Проведенное аналитическое моделирование по системе уравнений (2) с использованием специально разработанного программного обеспечения [2, 3, 8] позволяет сделать вывод о высокой эффективности подобной балансировки, так как с одной стороны, обеспечивается уравнове- шенность ротора как твердого тела, а с другой – выполняются определенные динамические условия, гарантирующие работу ротора с достаточно низким уровнем вибрации по сравнению с неот-балансированным ротором (рис. 2).

На рис. 2 обозначено: y _k = r_k /r_{k 0} , где r_k , r_{k 0} - динамические прогибы в точках х = х_k отбалансированного и неотбалансированного роторов; у =1...12 обозначают различные сочетания условий, по которым определялись дисбалансы корректирующих масс; кривые Б(3) и Б(4) показывают уровень значений Y _k для ротора, отбалансированного по предлагаемой технологии соответственно в трех и четырех плоскостях коррекции, а кривая А показывает средне производственное значение y _k .

Полученные результаты (рис. 2) позволяют выбрать такой вариант балансировки, при котором обеспечивается минимальное значение у , то есть вариант оптимальный с точки зрения вибронадежности роторной системы.

Однако на выбор метода балансировки оказывают влияние и другие факторы, например, жесткие ограничения на значения корректирующих масс приводят к тому, что достаточно сложно обеспечить сочетаемость минимальных значений коэффициента у _k с приемлемыми значениями дисбалансов корректирующих масс D_i . Это особенно важно, когда коррекция дисбаланса достигается за счет съема металла, поскольку резерв съёма ограничен.

Поэтому наряду с точными методами расчета корректирующих масс нами был использован метод Монте-Карло, то есть метод статистического поиска.

Для реализации статистического поиска нами разработан программный модуль на базе программной оболочки MathWorks MatLab, реализующий статистическое моделирование указанной технологии балансировки. Алгоритм действия программного модуля представлен на рис. 3.

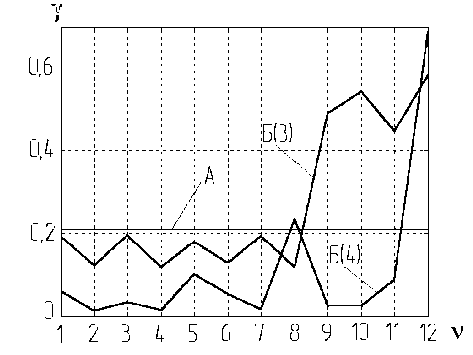
Рис. 2. Результаты расчета у ( v )

статистического моделирования

Здесь согласно результатам аналитического моделирования, за оптимальный аналитический вариант взят вариант со следующими условиями балансировки: a =4 – количество плоскостей коррекции; i =1, 4, 7, 8; T =2 – количество плоскостей, в которых устраняются динамические прогибы; с =4, 7 – номера плоскостей, в которых устраняются динамические прогибы. На рис. 3 обозначено: Q ₀ = 2(| A_n\ + | Bn |) ; § =1^1000 -число исследований, принятое нами для статистического моделирования.

Некоторые результаты расчета, проведенного с использованием разработанного программного модуля, по указанным оптимальным параметрам, аналитической модели, приведены на рис. 4 и 5, где обозначено: 1 – при аналитическом моделировании, 2 – при статистическом моделировании.

ВЫВОДЫ

• -    анализ рис. 4 и 5 показывает, что кривые 1 и 2 обладают схожей динамикой, причем, используя метод статистического поиска оптимально-

• Рис. 4. Значение Y при моделировании
0. Т, кг-1

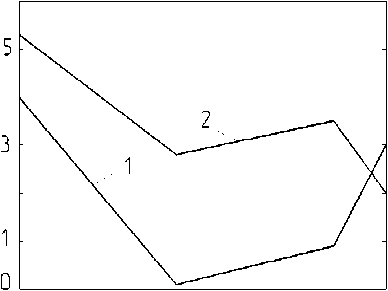
1                    4                   7     8

плоскости коррекции

Рис. 5. Значение Di при моделировании го решения, возможно определить не только более оптимальные параметры балансировки, но и добиться более равномерного распределения уровня вибрации по поверхности ротора (рис. 4, кривая 2);

• -    значения корректирующих дисбалансов при статистическом моделировании не намного превосходят соответствующие значения при аналитическом и отвечают необходимому резерву съёма материала при коррекции;

• -    отмеченные особенности, свидетельствуют о высокой сходимости аналитической и статистической моделей;

• -    применение подобного анализа в производстве играет существенную роль, так как аналитическая модель позволяет добиться нулевых значений динамических прогибов в определенных точках, при указанных динамических условиях. Это вызывает необоснованное повышение корректирующих дисбалансов, что недопустимо ввиду ограниченности резерва съема металла при коррекции. Используя статистическое моделирование, возможно наиболее равномерно распределить корректирующие дисбалансы по поверхности ротора;

• -    проводить подобный анализ возможно для каждого конкретного ротора и на стадии его проектирования, на основании данных вероятностного расчета начальных дисбалансов.