Имитационное моделирование бизнес-процесса "Строительство быстровозводимых зданий". Часть 2. Разработка статистической имитационной модели

На основании постановки задачи исследования бизнес-процесса «Строительство быстровоз-водимых зданий» [1] методом статистического имитационного моделирования (СИМ) по версии метода Димова-Маслова (МДМ) [2], а также по результатам комплексного анализа бизнес-про-цесса, в том числе его статистического исследования, во второй части статьи представлены результаты разработки алгоритма СИМ по МДМ, включая определение исходных и других данных, необходимых для моделирования.

Определение состава исходных данных

Одной из важных задач СИМ является определение влияния случайных факторов в интересах управления процессом и поиска возможностей его улучшения. В результате анализа бизнес-про-цесса [1] выявлено, что он подвержен влиянию порядка 40 случайных факторов, причем воздействие на результаты СИМ 20 из них оценивается экспертами как существенное.

Случайные факторы представлены набором случайных величин (СВ), каждая из которых характеризуется законом распределения, тип и параметры которого приведены в таблице 1: ‒ интенсивность поступления заявок СВ1;

‒ длительность обработки заявок СВ2;

‒ длительность исследования места строительства СВ3;

‒ время разработки технического задания СВ7;

‒ количество индивидуальных проектов СВ10;

‒ длительность формирования календарно-сетевого графика СВ11;

‒ время разработки концептуального проекта СВ14;

‒ время разработки системного проекта СВУ15;

‒ время разработки детального проекта СВУ16;

‒ длительность согласования проекта в государственных инстанциях СВ21;

‒ количество отказов по несогласованию в государственных органах СВ22;

‒ длительность производства материалов ‒ металлоконструкций для строительства СВ24;

‒ количество заявок с недостаточным запасом сырья для производства СВ25;

‒ длительность производства материалов СВ26;

‒ количество некачественно произведенного материала СВ30;

‒ длительность доставки материалов на место строительства СВ31;

‒ количество неполных комплектов материалов СВ33;

‒ длительность монтажа здания СВ34;

‒ количество возведенных не по стандарту зданий СВ38;

‒ длительность ввода здания в эксплуатацию СВ39.

Поскольку случайные факторы могут быть как основными, так и второстепенными, не все перечисленные СВ одинаково влияют на результаты СИМ. Это следует иметь в виду при идентификации СВ и реализации имитационного эксперимента. За основные примем факторы, оказывающие наибольшее влияние на анализ и управление бизнес-процессом.

Идентификация законов распределения осуществляется по классическому алгоритму [3]. В результате обработки случайной выборки по каждому отобранному фактору выявлено, что законы распределения данных СВ близки к закону Пуассона, нормальному и экспоненциальному законам. В качестве примера в таблице 2 при- ведены числовые данные для построения гистограмм, которые характеризуют три типовых СВ с указанными законами распределения

Из таблиц 1-2 видно, что нулевая гипотеза относительно СВ1 состоит в том, что генеральная совокупность ее значений распределена по зако- ну Пуассона. Объем выборки N = 100, число интервалов S = 8, величина интервала (шаг) i = 1,

X max = 8, X min = 0.

Проверим нулевую гипотезу при уровне значимости а = 0,05 в соответствии с критерием согласия х 2 хи-квадрат Пирсона. По таблице критических точек распределения х 2 при числе степеней свободы 7 определим критическое значение Х 2 _крит и вычислим наблюдаемое значение Г„.л. Так как Х 2» = 12,48 <х кр„ = 14,07, ™. данном случае нет оснований отвергнуть нулевую гипотезу.

Τаким образом, в результате обработки статистического материала выявлено, что СВ1 корректно аппроксимировать пуассоновской СВ с параметром X = 2,06.

Определим закон распределения СВ2. Пусть нулевая гипотеза состоит в том, что закон распределения СВ2 наиболее близок к экспоненциальному. Объем тестовой совокупности N = 100, число интервалов соответственно 8, X max = 41,29, X mm = 0,13, шаг интервала i = 5. Проверим гипотезу, вычислив теоретические вероятности и наблюдаемое значение критерия Пирсона. Поскольку x ' ,^ = 9,90 < / 2^ = 12,59 и расхождение теоретических и эмпирических вероятностей незначительно, то принимаем нулевую гипотезу и моделируем СВ2 как распределенную по показательному закону.

Аналогичным образом проанализируем СВ3. В этом случае нулевой гипотезой является пред-

Τаблица 1. Случайные величины, влияющие на моделируемый бизнес-процесс

Закон	Пуассона							Экспоненциальный
Параметр	СВ1	СВ10	СВ22	СВ25	СВ30	СВ33	СВ38	СВ2
х = X B	2,06	3,65	0,96	1,99	1,75	2,09	1,05	X B = 12,48
D ( х )	1,76	2,51	0,98	2,17	1,63	1,96	1,33	Х = 0,08
а	1,33	1,59	0,99	1,47	1,28	1,40	1,15	а = 9,83

Τаблица 1 (окончание)

Нормальный закон
Параметр	СВ3	СB7	СB11	СB14	СB15	СB16	СB21	СB24	СB26	СB31	СB34	СB39
X в	14,4	10,05	14,02	4,88	2,49	3,09	13,20	6,27	10,47	5,34	11,14	4,79
а	2,84	2,58	5,49	2,69	1,76	1,84	3,97	1,94	2,26	1,81	3,03	2,23

Τаблица 2. Значения частостей W_i случайных величин СВ1, СB2 и СВ3

Интервал	1	2	3	4	5	6	7	8
СB1	0,10	0,25	0,32	0,21	0,09	0,02	0,00	0,01
СB2	0,31	0,22	0,14	0,12	0,10	0,05	0,03	0,03
СB3	0,01	0,06	0,18	0,29	0,21	0,16	0,07	0,02

:В22 <= Pgovem agreei

( НАЧАЛО

Нет

Нет

17-31

6-12

13-16

( КОНЕЦ )

Моделирование интенсивности поступления заявок СВ1. Изменение времени поступления зоследней заявки на величину СВ1: t += СВ1;

Моделирование времени согласования проекта в государственных инстанциях СВ21 и сдвиг модельного времени: t += СВ21;

Инкремент счетчика заявок на строительство БВЗ: kreq_in++;

Моделирование проектирования быстровозводимого здания

Моделирование разработки технического задания

Объявление и инициализация переменных и переметров

Моделирование события "проект согласован в государственных инстанциях" СВ22

Расчет итоговых показателей и значений переменных

Вывод результатов моделирования на экран

Моделирование обработки заявки

Ввод исходных данных

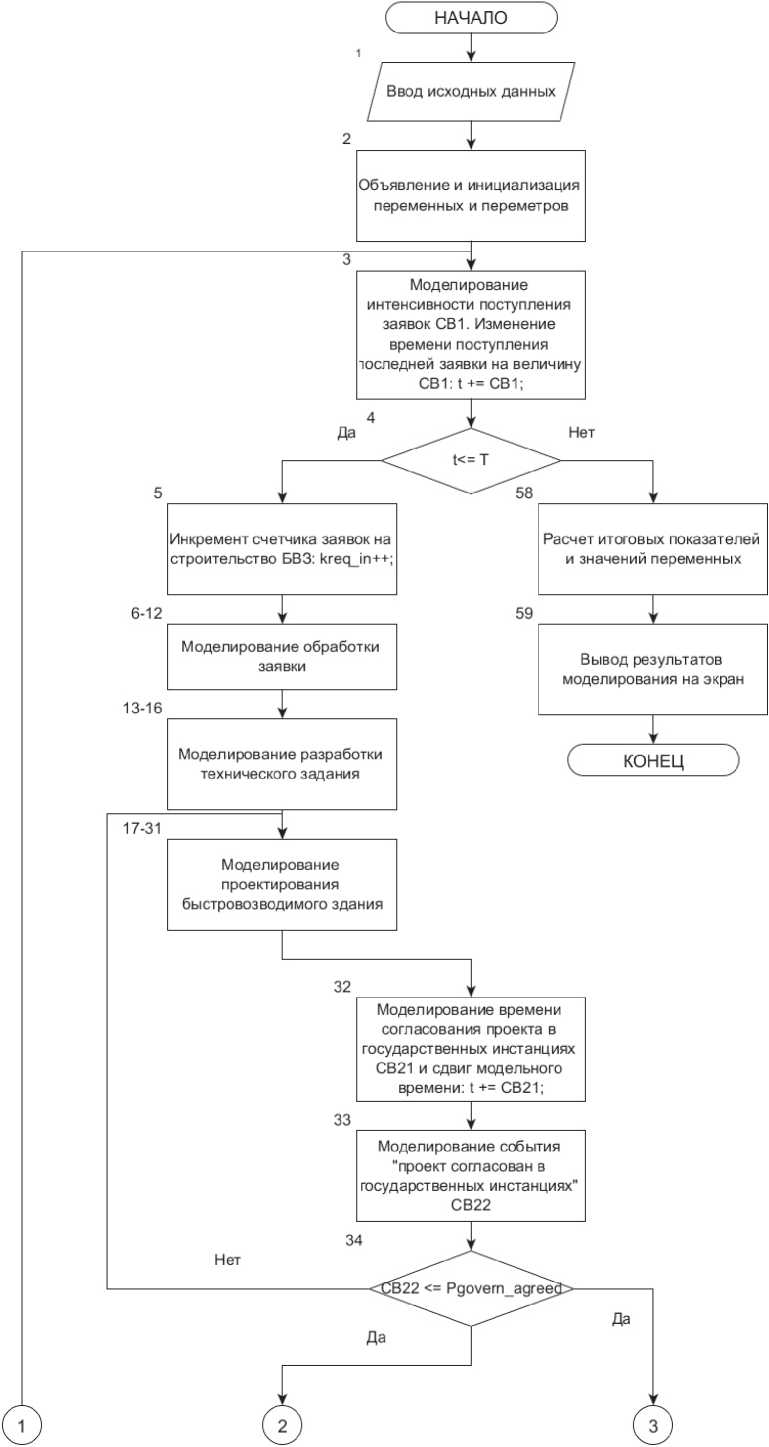
Рисунок 1. Частично детализированная схема моделирующего алгоритма

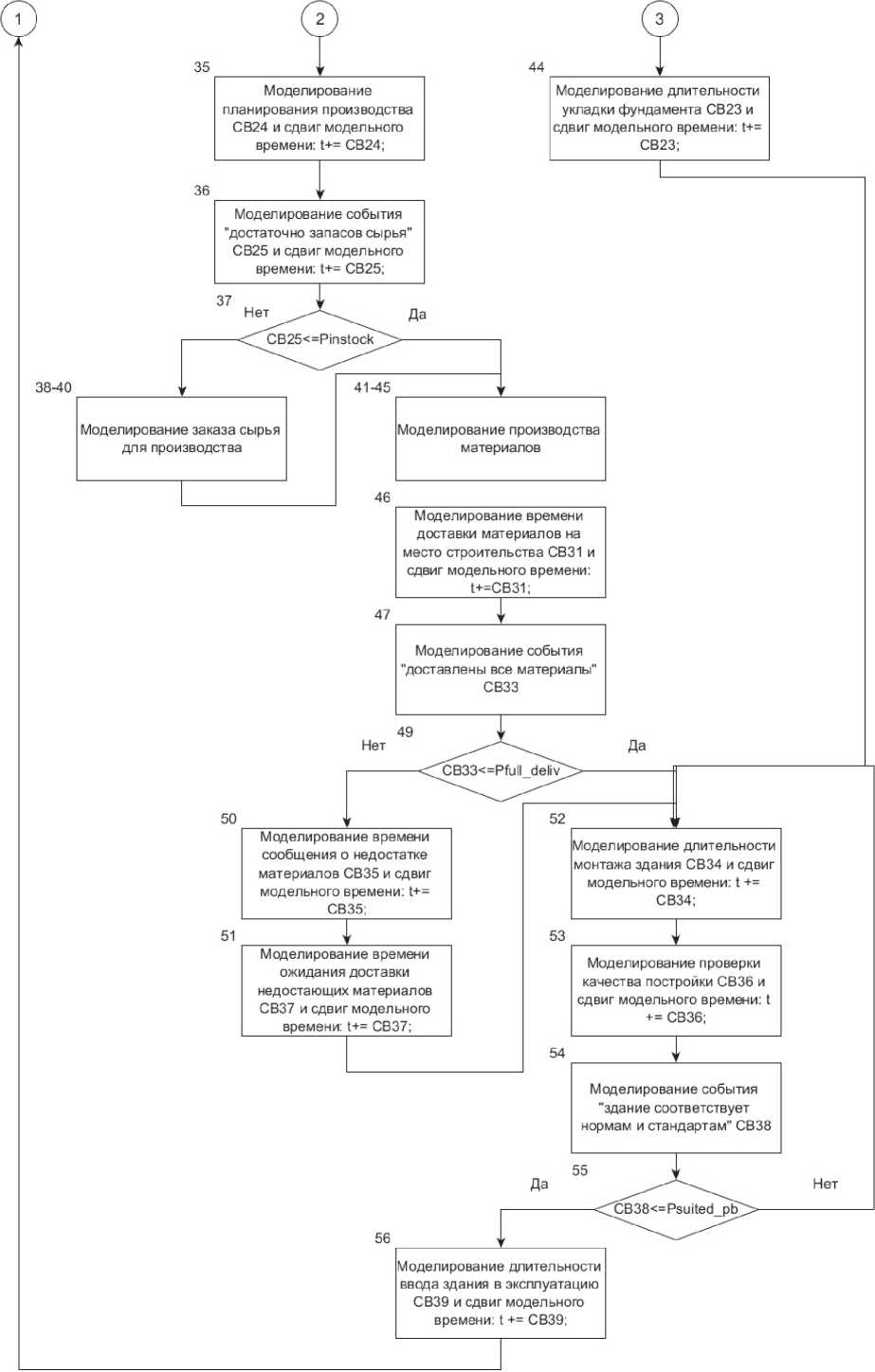
Рисунок 1 (окончание)

положение о нормальном распределении СВ3. Объем выборки и число интервалов : 100 и 8 соответственно, Х„„ = 22,3, X.= 6,54, шагин-max               min тервала i = 2.

Так как ^ = 1,90 <  х^ = 11,07, то нет основания отвергнуть нулевую гипотезу и в процессе моделирования СВ3 можно аппроксимировать но рмально распределенной СВ с параметрами Х в = 14,40 и о = 2,84.

Разработка и описание алгоритма СИМ по МДМ бизнес-процесса

Модель бизнес-процесса реализует предварительно разработанный моделирующий алгоритм ‒ схематическое описание операций, выполняемых компьютером в ходе СИМ по МДМ. Моделирующий алгоритм отображает изменение дискретных состояний исследуемой системы в непрерывном масштабе времени. В процессе выполнения этого алгоритма происходит аккумулирование статистических данных в параметрах и переменных модели, а также генерирование соответствующих таблиц и графиков.

Моделирующий алгоритм должен обладать следующими свойствами [4]:

‒ одновременное моделирование ряда независимых событий в единицу модельного времени; ‒ независимость от структуры процесса;

‒ небольшие затраты вычислительных ресурсов;

‒ простота и гибкость.

Моделирование является итеративным про-цессом։ блоки моделирующего алгоритма представляют собой итерации, соответствующие элементарным событиям процесса. В бизнес-про-цессе строительства быстровозводимых зданий нельзя заранее вычислить моменты изменения состояния процесса, в связи с чем используется моделирующий алгоритм со случайным шагом с длительностью, выраженной случайной величиной [11].

На рисунке 1 представлена частично детализированная схема моделирующего алгоритма, которая, с одной стороны, отражает особенности исследуемого бизнес-процесса, а с другой представляет тривиальные последовательности операций в укрупненном виде. Так, например, подпроцесс проектирования изображен на схеме одним блоком, который на самом деле является агрегатом серии аналогичных блоков 17‐31, каждый из которых моделирует отдельный шаг данного подпроцесса.

Моделирующий алгоритм позволяет учесть специфическую особенность бизнес-процес-са строительства быстровозводимых зданий։ во время производства на заводе строительных конструкций на месте строительства выполняется укладка фундамента. Подробное описание работы алгоритма представлено в диссертационной работе [12].

Для каждого интервала модельного времени генерируются значения случайных величин, а также выполняется подсчет оценок контролируемых характеристик по собранным статистикам.

По окончании моделирования выполняется расчет контролируемых показателей и вывод на экран диаграмм и графиков накопленных статистических данных [4].

Выводы

В [5‐7 и др.] отражен подход к быстровозводи-мым конструкциям как сложноструктурированным техническим системам [8]. При этом основными методами изучения выступают системный анализ и индивидуальные экспертные методы. Новизна данного исследования заключается в том, что впервые строительство быстровозводи-мых зданий и комплексов рассматривается в качестве сложного бизнес-процесса эффективное функционирование которого зависит от влияния множества случайных факторов. В контексте этого подхода предлагается применять СИМ по МДМ для углубленного анализа бизнес-процесса и управления им. В интересах СИМ определена детализированная схема исследуемого бизнес-процесса, разработаны статистическая модель и алгоритм моделирования, ранее не освещенные в научных исследованиях подобных бизнес-про-цессов.

Во второй части статьи получены следующие результаты։

‒ выполнен анализ исследуемого бизнес-про-цесса в интересах имитационного моделирования и управления, в результате которого выявлены случайные факторы, отрицательно влияющие на показатели его качества функционирования;

‒ в результате экспертной оценки выявленных случайных факторов выполнена их диверсификация на основные и второстепенные по степени влияния на СИМ по МДМ, из 40 факторов выбрано 20, которые были учтены при разработке модели;

‒ выбранные случайные факторы описаны в терминах СВ, произведена идентификация зако- нов распределения данных СВ в интересах СИМ по МДМ;

‒ определены и инициализированы начальными значениями параметры и переменные имитационной модели։ параметры передают в модель входные, начальные значения ключевых показателей бизнес-процесса, переменные отражают контролируемые данные в динамике и служат для расчета выходных значений показателей;

‒ на основании описанной в первой части статьи [1] схемы бизнес-процесса построена обобщенная структурная схема моделирующего алгоритма, которая отражает общий порядок действий при моделировании и процесс взаимодействия пользователя с имитационной моделью от ввода исходных данных до вывода на экран результатов в виде значений переменных и графиков;

‒ приведен фрагмент детализированной схемы алгоритма, уточняющей шаги моделирования в соответствии с особенностями рассматриваемого бизнес-процесса;

‒ разработанный алгоритм моделирования является техническим заданием на разработку программного обеспечения имитационной модели бизнес-процесса «Строительство быстровозво-димых зданий».