Имитационное моделирование частотно-регулируемых электроприводных газоперекачивающих агрегатов компрессорных станций

Критерии разработки математической модели электроприводного газоперекачивающего агрегата (ЭГПА)

Для строящихся технологических установок систем объектов топливных энергетических комплексов (ТЭК) [1–3] необходимо обеспечить большие мощности подводимой электроэнергии с высоким напряжением питающей сети и созданию отдельных трансформаторных подстанций (ТП) (рис. 1) [4–6].

Реальный технологический процесс исключает возможность проведения экспериментов на работающем оборудовании, поскольку это может привести к неконтролируемым последствиям. Один из возможных выходов – это построение математических моделей по параметрам реальных объектов [7–9].

Один из вариантов разработки таких моделей можно проследить на базе газоперекачивающего агрегата как основного элемента ТЭК. В качестве примера моделирования выбран мощный электропривод ЭГПА [10–12] с частотным регулированием. Главные параметры ЭГПА сведены в табл. 1 [13–15].

Предлагаемая компьютерная модель строилась по описанию алгоритма работы реального электропривода в составе ЭГПА. Выбранный вариант программного обеспечения пакет MATLAB Simulink позволил выполнить разработку структурной схемы модели ЭГПА с частотным регулируемым приводом, который представлен на рис. 2.

Рис. 1. Внешний вид КТП

Fig. 1. General view of a complete transformer substation

Таблица 1

Table 1

Главные технические параметры ЭГПА

Main technical parameters of EGPA

Наименование параметра	Ед. изм.	Значение
Номинальное напряжение на входе	В	10 000
Производительность объемная, отнесенная к начальным условиям 20°С и 0,1013 МПа	МЛН м3/суг	12,5
Степень сжатия	о.е.	1,26
КПД привода в номинальном режиме	о.е.	0,92
Мощность привода механическая номинальная	кВт	4 000
Частота вращения номинальная	об/мин	8 200
Диапазон рабочих частот вращения, % от номинальной	%	от 70 до 105

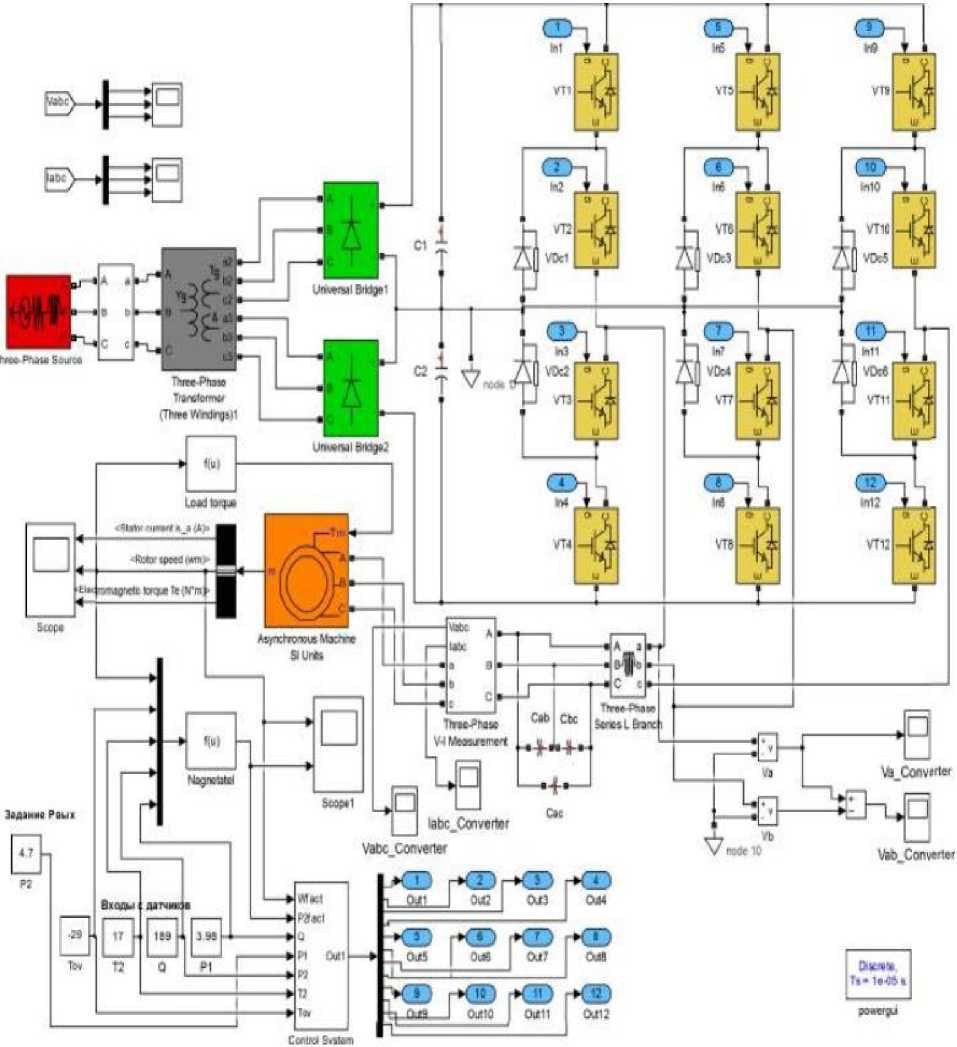
Рис. 2. Структурная схема модели Fig. 2. Structural diagram of the model

В разработанный вариант структурной схемы введены:

• -    трехфазный асинхронный электродвигатель (блок Simulink – Asinchronous Machine);

• -    силовой трансформатор на основе Simulink – Three-Phase Transformer;

• -    центробежный нагнетатель на базе функции MATLAB;

• -    трехфазный источник напряжения для моделирования промышленной сети с параметрами 10 кВ 50 Гц;

• -    преобразователь частоты созданный по клас-

• сической схеме из выпрямителя (блок Simulink – Universal Bridge) и автономного инвертора напряжения (проектируемый блок Simulink);

• -    на выходе ПЧ применён фильтр (блок Simu-link);

• -    САУ, в основу которой заложен проектируемый блок Simulink – Control System;

• -    блоки измерения и контроля электрических и механических параметров Simulink – Three-Phase V-I Measurement, Va, Vb Vс;

• -    для контроля и вывода цифровых параметров системы добавлен блок Simulink – Scope.

Центробежный нагнетатель

На основе метода регрессионного анализа по методике, изложенной в статьях [16–18], выведено уравнение работы центробежного нагнетателя. Этот подход дал возможность максимально точно учесть зависимость основных параметров центробежного нагнетателя от всех влияющих внешних факторов [19–21].

Моделирование электрической сети

Типовой блок библиотеки SimPowerSystem – Three-Phase Source позволил смоделировать силовую электрическую сеть трехфазного напряжения. Для его программирования использованы исходные параметры, представленные в табл. 2.

Модель силового электродвигателя

В промышленном варианте ЭГПА используется асинхронный электродвигатель 1TA 2832-4AU01-Z. Его производство осуществляет фирма Siemens. В математической модели он взят в качестве прототипа. Основные его электрические и механические параметры представлены в табл. 3. Нагрузка привода принята как вентиляторная.

Моделирование ПЧ

Для моделирования ПЧ выбрана реальная схема с явно выраженным звеном постоянного тока. Схема включает в себя нерегулируемый выпрямитель с двумя конденсаторами на выходе и автономный инвертор напряжения.

Таблица 2

Таблица 3

Таблица 4

Параметры модели электрической сети

Table 2

Parameters of the electrical network model

Параметр	Ед. изм.	Значение
Действующее значение линейного напряжения	В	10000
Частота	Гц	50
Мощность к.з. в точке подключения	МВА	300

Параметры асинхронного двигателя 1ТА 2832-4AU01-Z

Table 3

Parameters of asynchronous motor 1TA 2832-4AU01-Z

Наименование параметра	Единицы измерения	Значение
Номинальное напряжение питания	В	3300
Мощность электродвигателя номинальная	кВт	4000
Мощность максимальная длительная	кВт	4200
Номинальная скорость вращения	Об./мин	8200
КПД номинальный	о.е.	0,958
Коэффициент мощности номинальный	о.с.	0,75
Момент номинальный	Нм	4658
Ток номинальный	А	970
Максимальный длительный ток	А	1008
Момент инерции ротора	КТ NT	48
Масса	КГ	15500

Параметры трансформатора

Transformer Parameters

Table 4

Наименование параметра	Единицы измерения	Значение
Номинальная мощность	кВА	6300
Номинальное напряжение первичной обмотки	В	10000 (с возможностью регулирования ±2x2,5%
Номинальные напряжения вторичных обмоток	В	1700
Напряжение КЗ	%	7

Выпрямитель смоделирован на основе стандартных блоков штатной библиотеки SimPowerSystem. Электрические параметры реального электрического трехфазного трансформатора взяты из табл. 4.

Инвертор напряжения выполнен по классической мостовой схеме Математическая модель в программном комплексе пакета MATLAB Simulink выполнена по такой же структуре. В разработанную модель вошли:

• –    блоки VT 1– VT 12 (блок Simulink – IGBT/Diode), выполненные на IGBT-транзисторах. Их параметры U н = 1 700 В, I н = 1200 A. Схема выполнена с обратными диодами;

• –    силовые диоды VD с 1 – VD с 6 .

В соответствии с законами ШИМ управляющие сигналы IGBT модулей формируются системой автоматического управления.

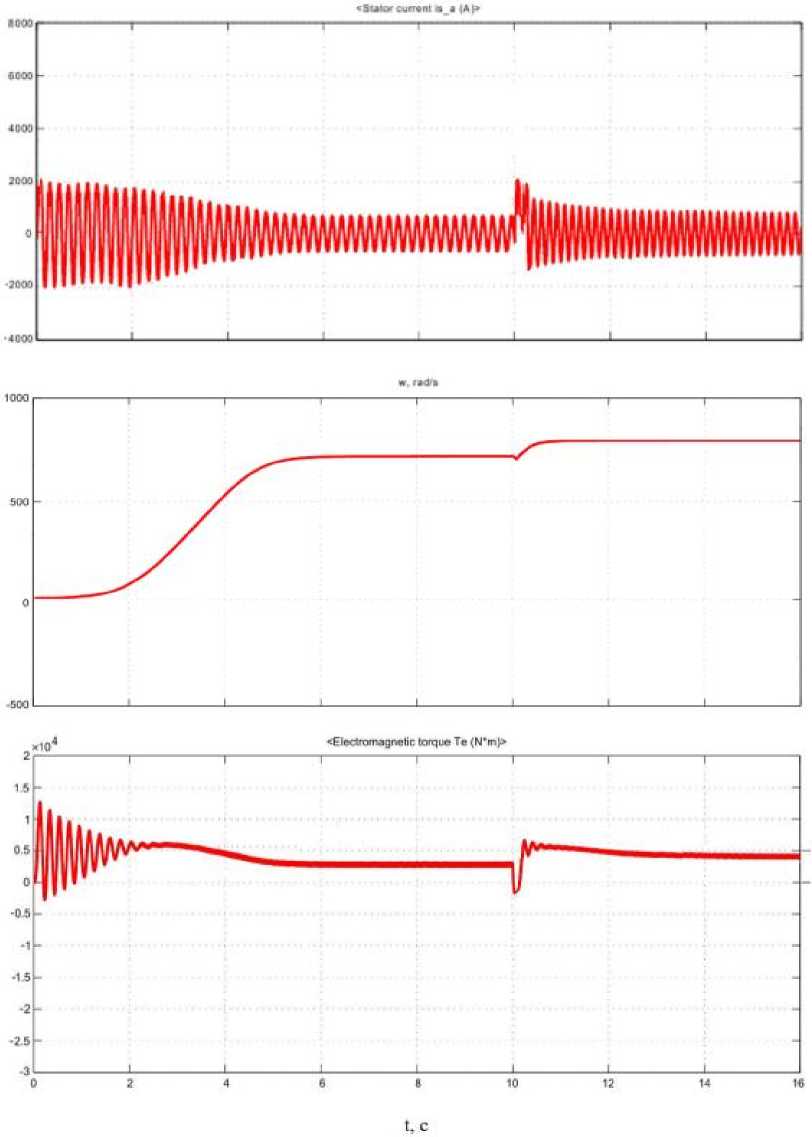
Рис. 3. Результаты моделирования пуска и регулирования скорости Fig. 3. Simulation results of start-up and speed control

Моделирование системы автоматического управления

Согласно исследованиям учёных П.А. Захарова и А.С. Хлынина удобнее всего выбрать схему системы регулирования скорости ЭГПА со стабилизацией давления на выходе с комбинированной структурой [22–25]. Главным параметром, подлежащим контролю, является давление на выходе ЭГПА.

В математической модели для реализации регулирования величины выходного напряжения инвертора выбран вариант стандартного блока ШИМ. В качестве алгоритма работы системы выбран следующий закон управления: при снижении частоты питающего напряжения выходное напряжение инвертора уменьшается пропорционально квадрату изменения частоты.

Блок MATLAB Simulink – Fcn осуществляет задание скорости и выполняет расчет по регрессионному уравнению. Регулирование скорости осуществляется с использованием в схеме ПИД-регулятора. В качестве такого регулятора применен стандартный блок MATLAB Simulink – PID Controller. Выходной сигнал задания скорости поступает на вход блока векторной ШИМ.

Результаты моделирования

По оценке результатов математического моделирования можно сделать ряд выводов по пред- ставленным графикам изменения тока статора, скорости вращения электродвигателя и электромагнитного момента. Результаты расчетных динамических характеристик ПЧ ЭГПА приведены на рис 3.

Из графиков хорошо видны момент пуска двигателя и набор скорости. Все процессы происходят плавно, без существенных колебаний и скачков, перерегулирование отсутствует. Можно наблюдать стабилизацию скорости и давления на выходе. При анализе графиков режимов работы ПЧ с ШИМ выполнены показатели качества электроэнергии питающей сети [21].

Коэффициент гармонических искажений питающей сети составляет 6 %, при допустимом значении – 10 % (рис. 4, 5).

Для улучшения гармонического состава выходного тока и напряжения возможно применение фильтров. Расчет фильтров осуществляется исходя из резонансной частоты 500 Гц. Возможно применить следующие параметры фильтра: С = 0,1 мкФ, L = 4 мГн. Полученный суммарный коэффициент гармонических искажений выходного напряжения ПЧ в статическом режиме с использованием LC-фильтра составляет 0,17 %, что не превышает допустимый порог в 5 %.

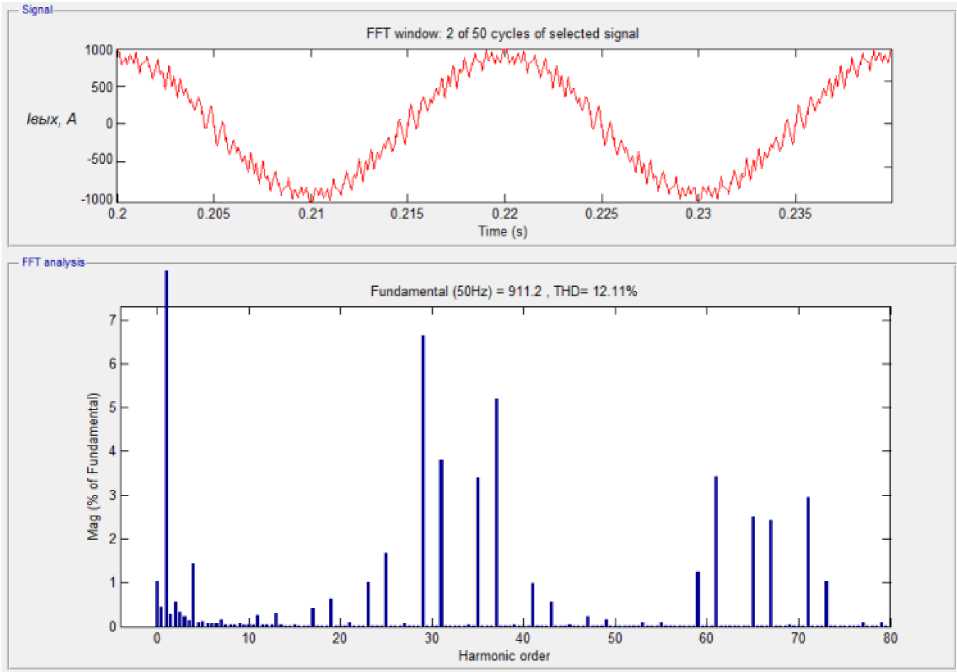
Рис. 4. Гармонический анализ сигналов

Fig. 4. Harmonic signal analysis

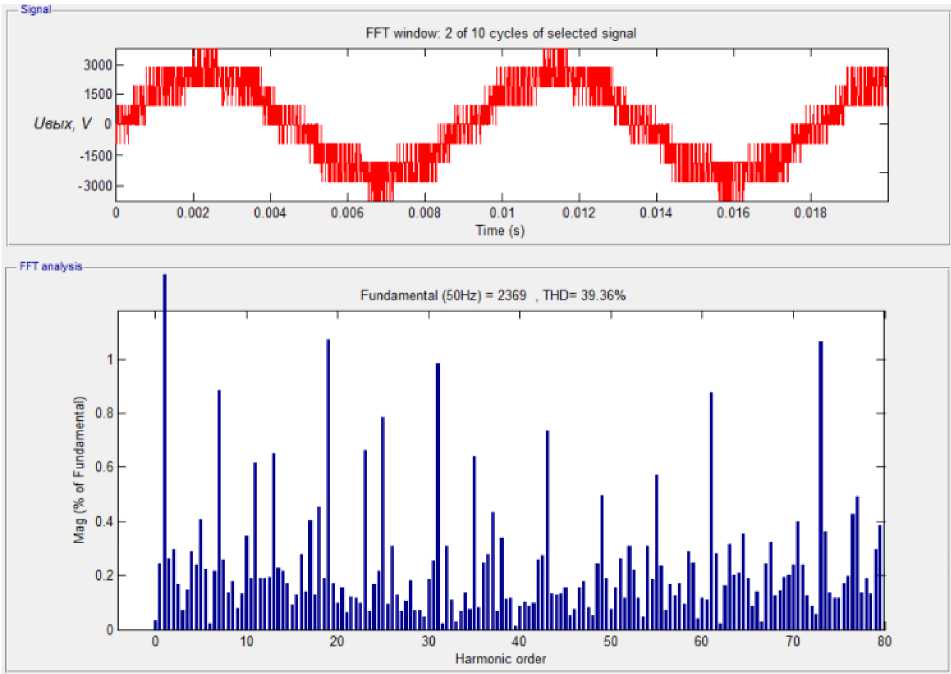
Рис. 5. Гармонический анализ сигналов

Fig. 5. Harmonic signal analysis

Выводы

• 1.    Разработанная математическая модель на базе MATLAB Simulink описывает все электромеханические процессы системы частотного регулируемого ЭГПА с представленной САР и стабилизацией давления КС.

• 2.    Предложенная САР обеспечивает высокую точность регулирования ЭГПА. Интеграл квадрата ошибки составляет 0,014–0,015 %. Точность регу-

• лирования выходного давления имеет интеграл квадрата ошибки не более 0,098 %. Из результатов можно сделать вывод о том, что полностью сохранена устойчивость в статике и динамике.

• 3.    Выбранный вариант инвертора напряжения с векторной ШИМ подтверждает возможность получения значения коэффициента гармонических искажений напряжения не более 0,17 % при допустимом пороге в 5 %.