Имитационное моделирование генерации дислокационной петли в поле случайно расположенных дискретных препятствий

The results of computer simulation of planar dislocation loop emission by Frank-Read sourse of further evolution of the dislocation loop in a random field of point-like obstacles is represented. The obstracles by spectrum of their "strength" correspond to reactive and nonreactive forest dislocations. In these condisions intensive process " separation of dislocations loops "is observed. Necessity of the account (record-keeping) of the process in equations of the balance deformation of defects in mathematical models of plastic deformation is marked.

В работе [1] обоснован переход от традиционного представления дислокационной подсистемы бесконечными прямолинейными дислокациями к детальному изучению эмиссии дислокационной петли источником Франка Рида и ее эволюции в плоскости кристаллографического скольжения; проанализированы принципиальные трудности, возникающие на этом пути и выход их них посредством описания распространения кристаллографического скольжения методами имитационного моделирования: предложена модель генерации и эволюции дислокационной петли в плоскости скольжения, содержащей точечные случайно расположенные препятствия, и принципы ее алгоритмизации. По существу она является синтезом барьерной модели постоянного линейного натяжения (см. обзор [2]) со снятым ограничением квазипрямолинейности [2] и классической модели работы источника Франка-Рида [3] в вязком надбарьерном режиме [4.5] и от близких по назначению моделей отличается следующим’

• 1)    рассматривается существенно двухмерная эволюция дислокационной петли в плоскости скольжения произвольных размеров;

• 2)    зарождение кристаллографического сдвига и процесс его дальнейшего развития изучаются в рамках единой модели.

В [6] представлены результаты верификации этой модели для случая однотипных по прочности препятствий, в [7] - для дискретного спектра препятствий. В данной работе продолжаются эти исследования, а именно, приводятся результаты верификации модели применительно к монокристаллу меди, ориентированному для одиночного скольжения в плоскости <1!1> в направлении <110> с плотностью дислокаций леса 10^s см~². Значения параметров модели являются константами кристалла или однозначно определяются условиями машинных экспериментов, за исключением характеристик препятствий. Что же касается последних, то это серьезная самостоятельная задача, решение которой во многом предопределяется природой рассматриваемых препятствий. Мы их интерпретируем как точки пересечения дислокаций леса с плоскостью залегания источника. Поэтому препятствия естественным образом делятся на "сильные" и "слабые" (реагирующий и нерёагирующий пес) из-за существенного различия как в уровне напряжений, необходимых для их преодоления, так и в возможных механизмах преодоления. Предполагается, что:

• 1)    дислокации некомпланарных систем скольжения равномерно распределены по ориенгациям:

• 2)    распределение точек пересечения дислокаций леса с плоскостью залегания дислокации является случайным равномерным;

• 3)    число стопоров на единицу площадки моделирования равно плотности дислокаций леса.

Для выбранного кристалла, направления и плоскости скольжения существует 18 вторичных систем скольжения (18 типов стопоров). При пересечении скользящей дислокации с нереагирующей дислокацией леса на каждой из них образуется порог или перегиб, и происходит увеличение длины дислокации. Для того, чтобы произошло перерезание скользящей дислокацией дислокации леса, силами внешнего напряжения должна быть совершена работа, величина которой может быть равна энергии двух порогов или дтзух перегибов или сумме энергий порога и перегиба [8]. В зависимости от вектора Бюргерса дислокации леса этим энергиям отвечают следующие критические углы огибания: 172.7°, 169.9°, 169°, 165.3°, 1626°, 1616°, 1596°. 157.9°. Они несущественно отличаются друг от друга и могут быть представлены средним значением - 163.5°.

Во втором случае происходят дислокационные реакции. Предварительно должен проводиться расчет напряжений, при которых становится возможным преодоление каждого из продуктов дислокационных реакций. Величина сопротивления комбинированной дислокации ее диссоциации (сопротивление преодолению дислокационного соединения) зависит от ориентации дислокаций некомпланарных систем скольжения по отношению к плоскости залегания скользящей дислокации. Разумеется, при различной ориентации дислокаций леса меняется и протяженность дислокационных соединений. Однако общий вклад дислокационных соединений в плотность дислокаций невелик, он составляет лишь около 2% от плотности дислокаций [9], определяемой как длина дислокаций в единице объема. Поэтому представляется приемлемой замена дислокационных соединений, имеющих в действительности различную протяженность, точечными стопорами, для преодоления которых необходимо приложить к дислокационным сегментам, расположенным по обе стороны от стопора, такую же силу, как и в случае преодоления дислокационного соединения. При этих соглашениях мы просто выразили результаты многочисленных исследований наших коллег (Р.И. Куринной. Л.В. Ганзи. М.В. Зголич) по прочностям дислокационных соединений (библиография приведена, например, в [8-10]) в терминах критических углов огибания препятствий (табл. 1). Предполагается, что. как и в случае дислокационных соединений, преодоление таких "прочных" ("сильных") точечных стопоров осуществляется чисто силовым путем (без термических активаций) или по механизму Орована. В таблице с„ ф_кр1 - относительные концентрации и критические углы огибания стопоров I- го типа (1=1,5); стопоры 2.3.4.5 атермические. Успешные термоактивные попытки "разрешены' только на стопорах первого типа.

Таблица 1

Прочность дислокационных соединений __

i	Тип реакции	[9]	^рд-град
1	—	0.833	163.5
2	ВЛ, d + DB, с = DA, с	0.056	95.7
3	BA,d*АС, b=BC,d	0.027	127.2
4	BA, d + DB, a = DA	0.065	65.8
5	BA, d + DC, a=BD/AC	0.019	113.4

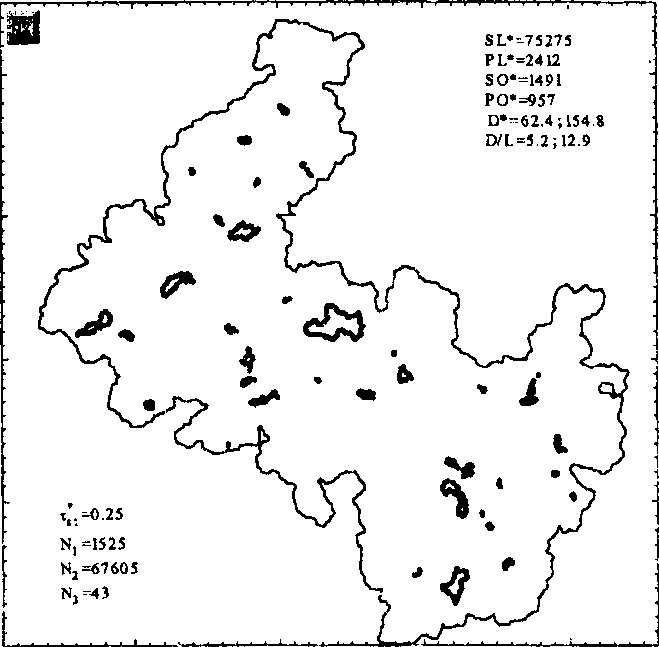
300            400

Рис.1. Дислокационная петля, сгенерированная источником (описание в тексте)

Таблица 2

Количественные данные об островах

/V	Р*	S*		число точек закрепления по типам					<г>
			Всего	5	3	2	4	1
1	1 2	3	4	5	6		8	9	10
1	| 6.63	1.46	6	0	?	0	2	2	1.105
2	16.73	16.97	12	0		3	6	2	1.3942
3	15.91	11.28	17	0	0	2	4	11	0.9359
4	6.15	1.94	8	0	0	1	3	4	0.7688
6	6.09	1.36	7	1	0	1	4	1	0.87
7	13.81	6.87	14	0	0	3	4	7	0.9864
8	20.04	18.05	14	0	0	3	7	4	1.431
9	62.41	104.25	38	4	0	2	20	12	1.642
10	60.07	119.55	41	3	1	10	13	14	1.465
И	52.14	118.1	32	1	2	6	13	10	1.629
13	36.94	37.59	27	0	4	3	7	13	1.3681
15	20.86	13.22	15	0	2	1	8	4	1.3907
19	16.47	16.59	12	0	0	3	5	4	1.3725
20	123.5	489.64	97	5	4	19	25	44	1.2732
22	25.64	30.42	20	1	3	3	6	7	1.282
23	30.16	45.29	20	2	1	1	8	8	1.508
24	21.03	16 64	17	2	0	4	4	7	1.2371
26	6.76	2.76	6	0	0	1	4	1	1.1267
28	30.82	15.65	21	0	0	1	11	9	1.468
29	46.61	47.81	33	7	0	8	12	11	1.4124
31	46.6	26.47	36	1	1	9	12	13	1.2944
32	10.62	2.57	10	0	0	3	3	4	1.062
33	26.3	29.39	24	0	1	6	7	10	1.0958
34	19.2	16.31	17	3	0	4	5	5	1.1294
35	8.57	4.3	7	0	0	0	6	1	1.2243
36	4.24	0.42	5	0	0	1	4	0	0.848
Зу	68.55	117.36	41	1	1	9	15	15	1.672
39	6.54	0.05	6	0	0	3	0	3	1.09
40	66.89	157.36	45	2	2	10	14	17	1.486
о	23.29	37.22	17.28	0.7	0.725	3.2	6.3	6.35	1.348

Организация моделирования обсуждена в [1]. Под действием приложенного напряжения дислокационный отрезок, шарнирно закрепленный в двух точках, начинает прогибаться, образуя ряд последовательных конфигураций, каждая из которых однозначно определяется набором огибания на "встречных" препятствиях и набором длин дислокационных сегментов. В [7] установлено напряжение старта источника (минимальное напряжение, при котором этот процесс приводит к эмиссии дислокационной петли) и отмечено, что за фронтом расширяющегося сегмента остаются "островки", представляющие трудно преодолимые участки плоскости скольжения, которые сегмент проходит по механизму Орована (рис. 1). По вполне понятным причинам на рисунке не показаны препятствия. Их на представленном фрагменте плоскости залегания источника более 200 тысяч. Дислокационным сегментом-источником к моменту образования петли, изображенной на рисунке 1, пройдено N₃ = 67605 препятствий, заметена площадь SL= 75275-1’ , петля "висит" на N, = 1525 стопорах, имеет периметр PL- 24121, . ее диаметр превысил первоначальную длину источника L--12 1, в 12,9 раза (здесь l_s = I / у[р . где р - плотность дислокаций леса), образовано N₃ = 43 острова общей площадью SO= 1491-1’ и периметром PL = 2412-1, . Значительна дисперсия в размерах островов, что видно на рис. 1. Количественные данные по островам сведены в табл. 2. в которой Л' -порядковый номер острова. Р*, S*, <Г> - соответствующие безразмерные параметры. площади и средние расстояния между стопорами вдоль дислокационной петли, ограничивающей остров. В оставшихся колонках таблицы "типы точек закрепления" соответствуют типам стопоров, представленных в Табл. I. Концентрация сильных препятствий в островах значительно выше, чем в поле препятствий, что легко заметить, сравнивая таблицы 1 и 2. Если для петли среднее расстояние между стопорами вдоль дислокации и их относительные концентрации стабилизируются в процессе скольжения, то для островов, в силу сравнительно небольшой статистики, этого однозначно утверждать нельзя. Однако, общая тенденция в том. что среднее расстояние между стопорами вдоль петелек, охватывающих острова, меньше I - соответствующего значения для петли, после которой остались эти острова. Хотя среди них есть и такие (они выделены в Табл. 2 специальным шрифтом), в которых эта общая тенденция нарушается или средние расстояния сравнимы. Для представленной здесь реализации это почти четверть всех островов, которые условно можно разделить на три группы: "сгустки, кластеры" из препятствий, в которых локальная плотность препятствий повышена по сравнению с площадкой моделирования, что вполне допустимо для действительно случайного поля стопоров - в противном случае оно было бы попросту упорядоченным. Для таких кластеров, а их около 77%. среднее расстояние между стопорами вдоль дислокации меньше Z . Они визуально различимы и их относительно легко можно выявить методами многомерного статического анализа, например, с помощью кластерного анализа или многомерного шкалирования. Примерно такая же часть островов с повышенной концентрацией сильных стопоров. Получающаяся сумма менее 100% естественно говорит о том. что существуют кластеры, обладающие обоими, признаками и их мы относим к третьей группе, к островам "переходного типа". Если теперь исключить пересечения, то в чистом виде островов первого типа около 14%, второго - 22%. Чувствительность к локальным флюктуациям в плотности стопоров зависит от приложенного напряжения. Понятно, что с увеличением напряжения она падает.

Кластеризация - характеристика именно случайного поля препятствий. Примечательно, что повторные машинные эксперименты при всех прочих равных условиях в том же случайном массиве стопоров и при том же источнике, но несколько сдвинутом в плоскости скольжения, приводит к тем же самым островам. То есть, острова воспроизводятся, однако последовательность их образования иногда отлична. То же относится к источникам разных длин, но с равными напряжениями старта. В случае несовпадения напряжений старта источников воспроизводятся лишь отдельные острова второго типа.

Несколько неожиданно, что доля площадки и периметра островов в площади, охватываемой расширяющимся сегментом и в его периметре, растет с расширением дислокационного сегмента (рис. 2). Эта доля к моменту образования петли довольно велика: для периметра около 30%, для площади 3-4%.

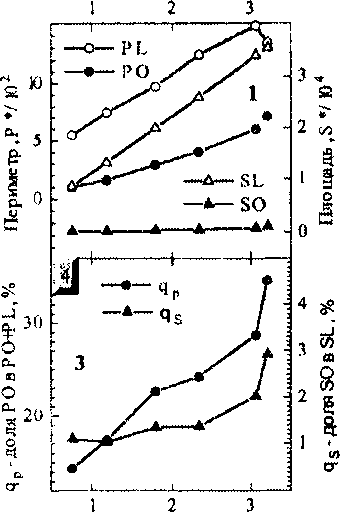
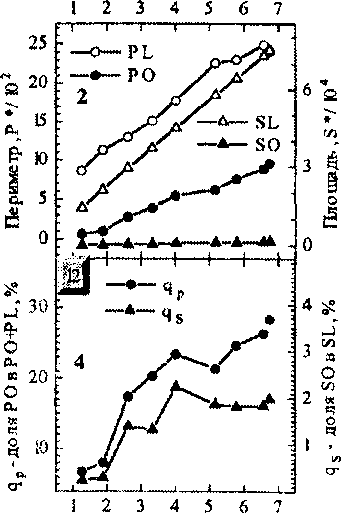
Число пройденных препятствий, N/ 10⁴

Рис 2. Зависимости общего периметра всех островов РО, периметра дислокационной петли, охватывающей эти острова PL, суммарной площади островов SO и площади SL, заметенной дислокационной петлей, от числа пройденных стопоров (1,2). На графиках 3,4 эти зависимости выражены в относительных единицах. Зависимости 1,3 для источника длиной 4-l_s; 2,4 -

12 ls

Большинство островов захлопываются в надбарьерном режиме, предварительно распадаясь на более мелкие (Рис. 3), часть из которых, в свою очередь, захлопывается через незначительное время с помощью термических активаций. Устойчивые острова наблюдались крайне редко.

В заключение отметим, что при моделировании работы источника Франка-Рида в однородном поле слабых препятствий островов за расширяющимся дислокационным сегментом не наблюдалось [6]. Аналогичная изложенной ситуация, по-видимому, будет иметь место всегда, когда в плоскости залегания источника присутствуют препятствия с существенно различными прочностями, а не только для леса дислокаций. Наблюдавшиеся острова больших размеров (охватывающие порядка полутысячи стопоров) еще раз убедительно показывают, что машинные эксперименты, связанные с распространением кристаллографического сдвига, необходимо проводить на достаточно представительном поле препятствий. Характеристики островов следует учитывать и при записи уравнений баланса деформационных дефектов, так как от их эволюции может значительно изменяться плотность дислокаций.

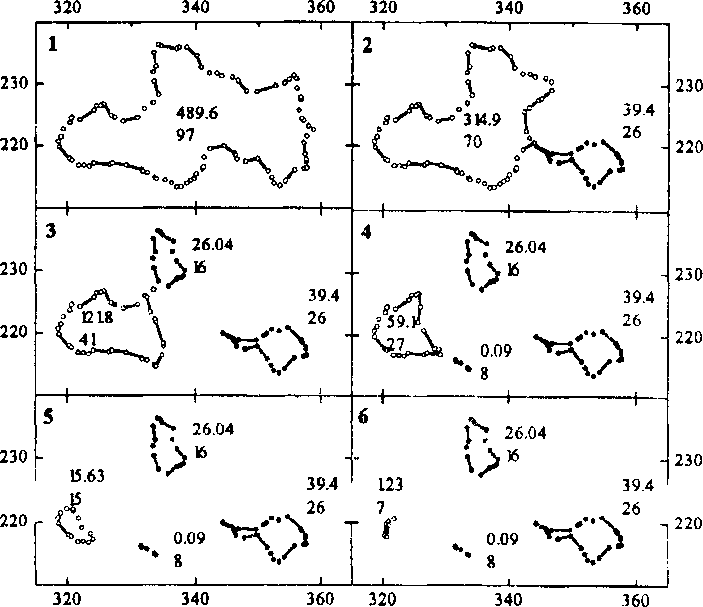
Рис.З. Эволюция острова N20 (см. табл.2). Цифрами в правых верхних углах занумерованы последовательности наблюдаемых в машинных экспериментах событий, пары чисел около островов - площади в единицах 1^ и число стопоров, на которых «висит» соответствующая дислокационная петля. Стопоры площадки моделирования не показаны, дуги окружностей, соединяющие соседние по дислокации стопоры, заменены отрезками прямых.