Имитационное моделирование и экспериментальное исследование трехфазного трансформатора с витыми ленточными плоскими и пространственными магнитопроводами

Конструктивной и механической основой трансформатора является его магнитная система (магнитопровод), которая служит для локализации в ней основного магнитного поля трансформатора. Магнитная система представляет собой комплект пластин или других элементов из электротехнической стали или другого электромагнитного материала, собранных в определенной геометрической форме [1].

Витой ленточный магнитопровод (рис. 1) для трехфазных трансформаторов характеризуется меньшей массой по сравнению с пластинчатым магнитопроводом, меньшими габаритными разме- рами при той же мощности, более высоким КПД. При изготовлении трехфазных трансформаторов с использованием витого ленточного магнитопровода уменьшается расход провода, снижается трудоемкость при намотке и сборке трансформатора [2].

Витая пространственная конструкция (рис. 2) за счет более равномерного распределения магнитного потока позволяет снизить массу магнитопровода и уменьшить потери холостого хода на 12–15 %. Конструкции ленточных магнитопроводов обеспечивают практически полную механизацию и частичную автоматизацию их изготовления и позволяют осуществить переход от стержня к ярму по кривой, совпадающей с направлением

а)

Рис. 1. Конструкция и габаритные размеры экспериментального образца витого ленточного плоского (а) и пространственного (б) магнитопроводов

б)

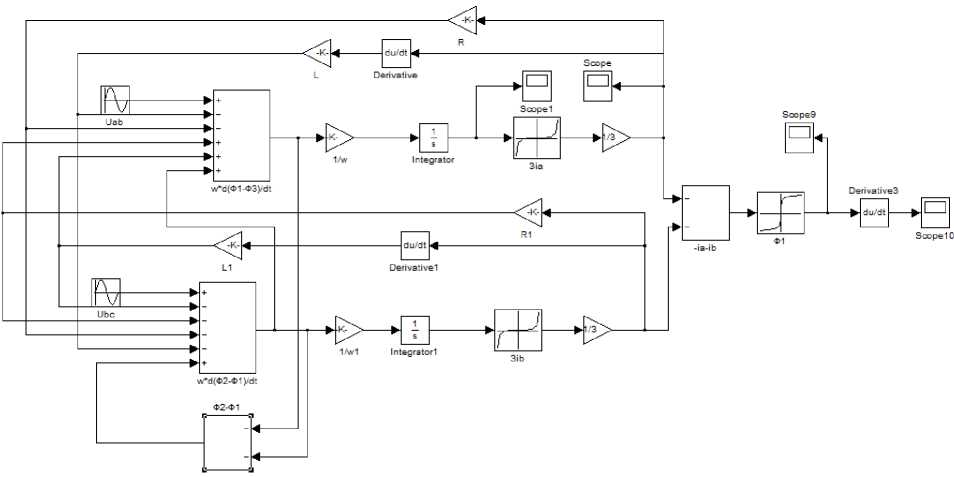
Рис. 2. Имитационная модель намагничивания трансформатора с витым ленточным плоским и пространственным магнитопроводами

магнитного потока, т. е. наиболее полно использовать анизотропные свойства холоднокатаной электротехнической стали [3].

Отличием витого ленточного плоского (рис. 1, а) и пространственного (рис. 1, б) магнитопроводов является разная длина пути магнитного потока для колец магнитопровода. Для витого пространственного магнитопровода она одинакова, а для плоского – разная. Из-за этого витой ленточный магнитопровод характеризуется небольшим отклонением от симметрии намагничивающих токов. Электромагнитные процессы в обоих магнитопроводах одинаковы.

Актуальность рассмотрения таких трансформаторов заключается в возможности компенсации потоков нулевой последовательности в соприкасающихся стержнях подобных трансформаторов [4–17].

Постановка задачи

Примем, что сеть, к которой подключен трансформатор, имеет бесконечную мощность и линейное напряжение сети не зависит от нагрузки. В схеме плоской навитой магнитной системы магнитный поток каждого стержня является геометрической суммой потоков двух навитых колец. Мгновенное значение потока в стержне фазы А можно представить в виде разности потоков а кольцах магнитопровода Ф A = Ф, - Ф1П, поток в стержне фазы B - Ф B = Фп - Ф,, поток в стержне фазы С - Ф С = ФП1 - Фп . Поскольку три кольца этой магнитной системы навиваются раздельно, а для удобства сборки между ними должен соблюдаться небольшой технологический зазор, переход магнитного потока из одного кольца в другое затруднен и фактически индукция в каждом кольце должна быть в 2/43 = 1,155 раза больше общей расчетной индукции в стержне [1].

Теоретическая часть

Для контура, включающего в себя фазы А и В , уравнение, составленное по второму закону Кирхгофа [5], будет иметь вид:

di A      d ^(Ф, ^{- Ф}ш)

UAb = iARA + LaA —77 + wA----т-- dtdt

,          di B      d (Ф_п - Ф , )

- iBRB - LaB    - WB-----7---- , dtdt где UAB – междуфазное напряжение в контуре, включающее в себя фазы А и В; iA , iB – токи в первичной обмотке фаз А и В соответственно; RA , RB – активные сопротивления первичной цепи фаз А и В соответственно; LaA , LaB - индуктивные сопротивления рассеяния первичной цепи фаз А и В соответственно; wA , wB – числа витков первичной обмотки фаз А и В соответственно; ФA , ФB – магнитные потоки фаз А и В соответственно.

Аналогично для контура, включающего в себя фазы В и С , уравнение будет иметь вид:

di B      d ^(Фц ^- Ф 1 )

UBC = iBRB + Lab "37 + wB----7-- dtdt

-CRc - LacdC - Wed<Ф™- Ф,,).(2)

dtdt где UBC – междуфазное напряжение в контуре, включающее в себя фазы В и С; iB , iC – токи в первичной обмотке фаз В и С соответственно; RB , RC – активные сопротивления первичной цепи фаз В и С соответственно; LaB, LaC - индуктив- ные сопротивления рассеяния первичной цепи фаз В и С соответственно; wB , wC – числа витков первичной обмотки фаз В и С; ФB и ФC – магнитный поток фаз В и С соответственно.

Уравнения, составленные по закону полного тока для магнитных цепей фаз А , В , С , имеют вид [5]:

iAwA - iCwC = H1 li;(3)

iBwB - iAwA = H2l2;(4)

iCwC - iBwB = H3l3,(5)

где H ₁ , H ₂ , H ₃ – напряженности магнитного поля в 1, 2 и 3 кольцах магнитопровода трансформатора соответственно; l ₁ , l ₂ , l ₃ – длины средних силовых магнитных линий в 1, 2 и 3 кольцах магнитопровода трансформатора соответственно.

Для первичных фазных токов при отсутствии нейтрального провода уравнение, составленное по первому закону Кирхгофа [18], запишется:

i A + i B + i C = 0 .

Запишем систему уравнений для трансформа- тора с витым ленточным плоским и пространст- венным магнитопроводами:

U AB =	diA i A R A + L a A —7- + wA dt	d (Ф 1 - Фш) dt
- i B R B	diB     d (Ф L a B      w B dt	II - Ф 1 ) . dt
U BC =	diB i B R B + L a B — + w B dt	d (Фп — Ф 1 ) dt
- i C R C	diC     d (Ф L a C      w C dt	III - ФП) , dt
i A w A -	i C w C = H 1 l i ;
i B w B -	i A w A = H 2 l 2 ;
i c w c -	i B w B = H 3 l 3 ;
. lA + lB	+ lC = 0.

а)

б)

в)

г)

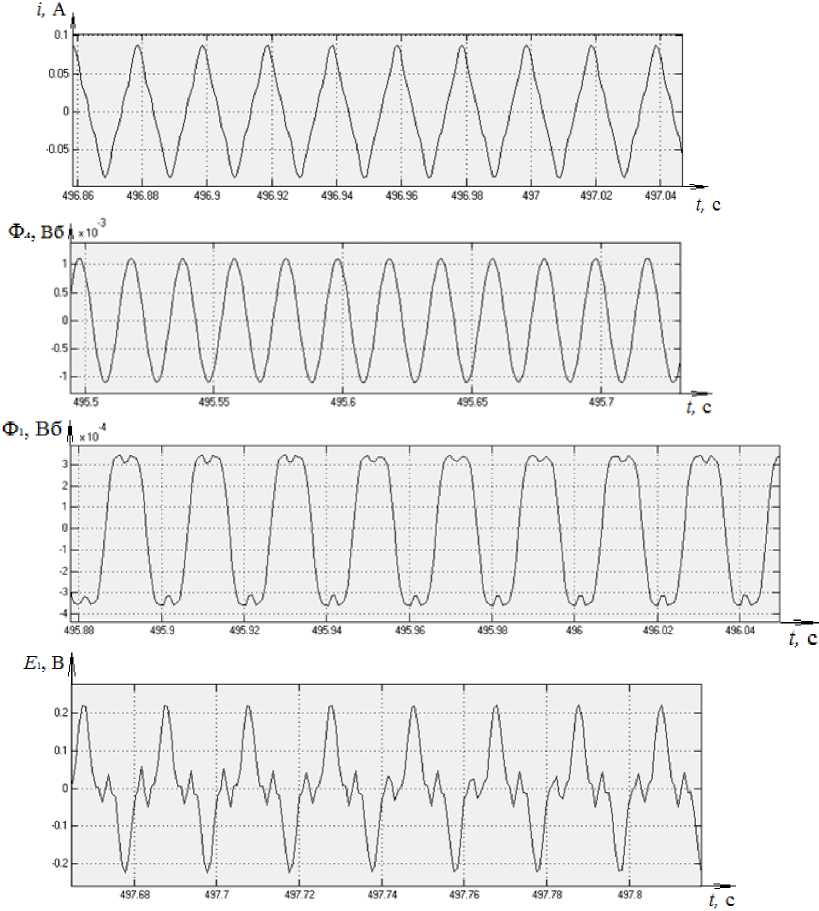
Рис. 3. Осциллограмма тока i_A (а), потока Ф _А в стержне (б), потока Ф₁ в кольце (в) и ЭДС E ₁ в стержне (г)

трансформатора с витым ленточным плоским и пространственным магнитопроводами

На основании систем уравнений (1)–(7) в программном пакете MatLab составлена имитационная модель намагничивания трансформатора с витым ленточным плоским и пространственным магнитопроводами (см. рис. 2) [19].

В результате моделирования были получены и проанализированы зависимости (рис. 3).

Как видим, кривая тока в фазе А трансформатора (рис. 3, а) несинусоидальна, но она не содержит гармоник, кратных трем. Поток Ф _А в стержне фазы А трансформатора (рис. 3, б) имеет практически синусоидальную форму, т. е. на выходе трансформатора искажения формы напряжения не будет. Поток в кольце трансформатора Ф_I (рис. 3, в) несинусоидален и имеет седлообразный характер [20]. На рис. 3, г представлена кривая изменения ЭДС E ₁ в кольце трансформатора. Как видим, ЭДС в кольце имеет заостренную форму и третью гармоническую составляющую.

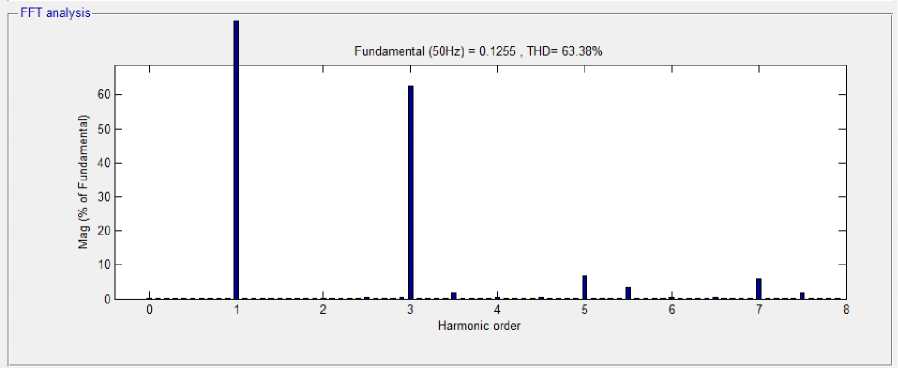
На рис. 4 представлены гармонические составляющие ЭДС E1 в кольце (рис. 4, а) и напряжения UA в стержне (рис. 4, б) трансформатора с витым ленточным плоским и пространственным магнитопроводами. Видно, что гармонические составляющие ЭДС E1 в кольце, помимо основной содержат третью гармонику (более 50 %). Гармонические составляющие напряжения UA в стержне трансформатора содержат только основную гармонику.

Для проверки адекватности имитационной модели был проведен эксперимент.

Практическая значимость, предложения и результаты внедрений, результаты экспериментальных исследований

Было проведено экспериментальное исследование трансформатора с витым ленточным плоским магнитопроводом со следующими параметрами (см. рис. 1, а):

• 1)    обмотки: первичные – 80 витков, вторичные – 20 витков, на одном стержне – 10.

• 2)    провод: ПЭВ-2, 5 = Ы0 " ⁶ м ² .

На рис. 5 представлена схема экспериментального исследования.

Для измерений параметров трансформатора использовался цифровой осциллограф (Fluke 124).

б)

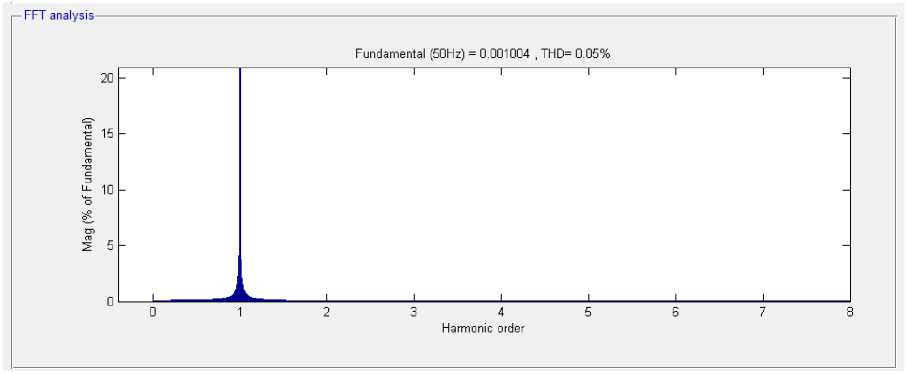
Рис. 4. Гармонические составляющие ЭДС E ₁ в кольце (а) и напряжения U_A в стержне (б) трансформатора с витым ленточным плоским и пространственным магнитопроводами

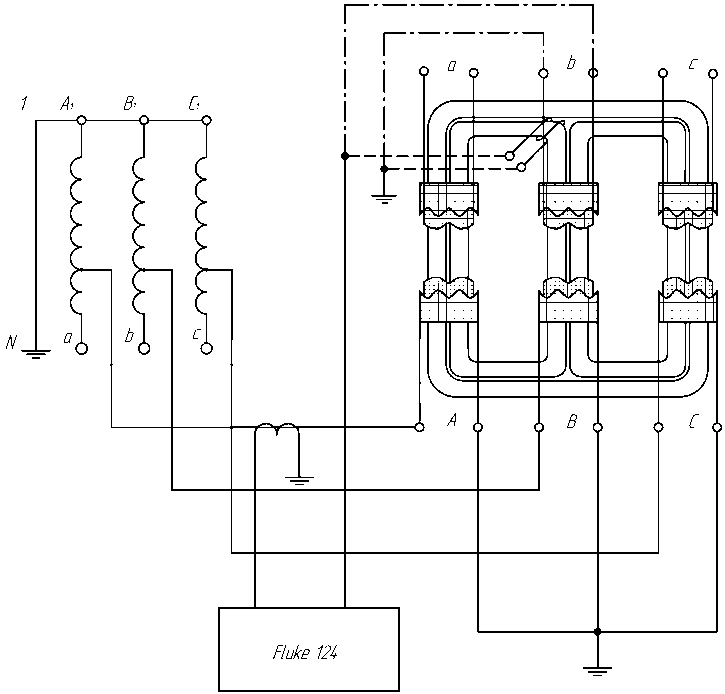
Рис. 5. Схема экспериментального исследования: 1 – автотрансформатор. Штриховой линией показано измерение напряжения в кольце, а осевой – измерение напряжения в стержне

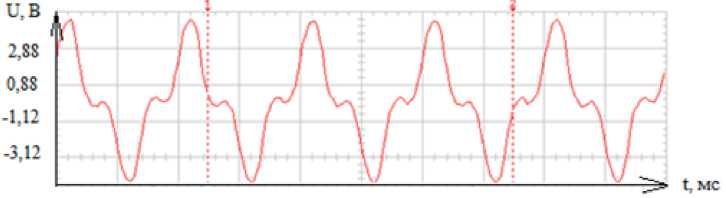
Далее приведены результаты экспериментального исследования трансформатора с витым ленточным плоским магнитопроводом: кривая напряжения фазы А в кольце трансформатора (рис. 6, а) и кривая напряжения в стержне фазы А трансформатора (рис. 6, б)

Как видим из рис. 6, а и 7, а, напряжение фазы А в кольце магнитопровода содержит третью гармоническую составляющую. А в напряжении фазы А в стержне магнитопровода содержится только основная гармоническая составляющая (рис. 6, б; 7, б).

а)

б)

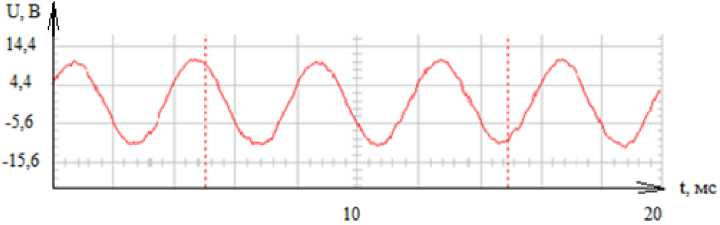
Рис. 6. Осциллограмма напряжения U ₁ в кольце (а) и напряжения U_A в стержне (б) трансформатора с витым ленточным плоским магнитопроводом

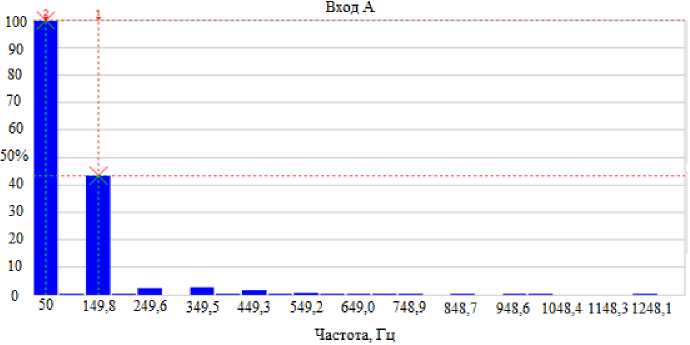
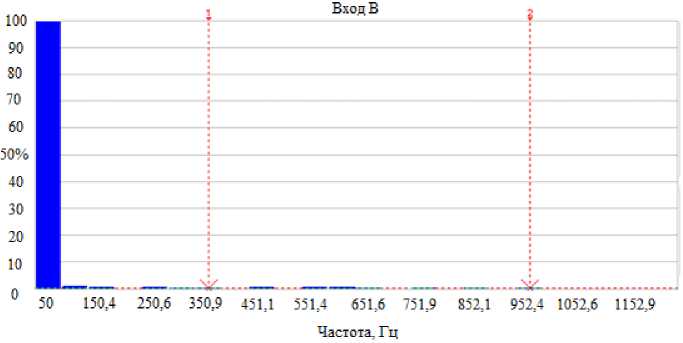
Рис. 7. Гармонические составляющие напряжения U ₁ в кольце (а) и напряжения U_A в стержне (б) трансформатора с витым ленточным плоским магнитопроводом

Заключение

В результате верификации было выявлено соответствие теоретических и экспериментальных исследований. Определено, что витой ленточный плоский и пространственный магнитопроводы содержат в напряжении третью гармоническую составляющую в кольце, а в стержне фазы – основную гармонику. Ток в стержне фазы несинусоидален, но не имеет гармоник, кратных трем. Поток в кольце несинусоидален и имеет седлообразный характер. Разница потоков, являющаяся потоком фазы трансформатора, синусоидальна. Таким образом, можно определить параметры схемы замещения трансформатора.