Имитационное моделирование инвестиционных рисков методом Монте-Карло

УДК 334                                                

Анализ и оценка рисков является одним из ключевых моментов в оценке общей эффективности инвестиционного проекта. При этом анализ рисков, связанных с инвестициями, должен быть проведен не только на этапе анализа и принятия управленческих решений, но и при дальнейшей реализации.

Неопределенность и риск являются неотъемлемыми свойствами инвестиционной деятельности фирмы. Инвестиционный проект разрабатывается, основываясь на определенных допущениях относительно постоянных и переменных затрат, объемов выпускаемой продукции, цен на товары, временных рамок проекта.

Вне зависимости от качества и целесообразности этих предположений, будущее развитие событий, связанных с реализацией проекта, всегда неоднозначно. Это главная аксиома любой предпринимательской деятельности. Результат инвестирования во многом зависит от того, насколько точно просчитана неопределенность и риск проекта.

Это предопределяет величину прибыли инвестора, получаемой от вложенного им капитала.

Поэтому для каждого инвестиционного проекта необходимо предварительно построить модель прогнозируемых потоков денежных средств, которая и будет являться моделью принятия решений в условиях неопределенности. На практике нельзя быть целиком уверенным, что при реализации инвестиционного проекта все денежные потоки будут в точности соответствовать прогнозируемым. С момента реализации проекта на каждом этапе будет возникать все большее и большее расхождение между прогнозируемыми и реальными денежными потоками. Может возникнуть ситуация, что рост цен на сырьё и материалы, изменение валютного курса, налоговых ставок или другие негативные события приведут к несостоятельности (банкротству) предприятия или, как минимум, к значительным дополнительным издержкам.

В    практике    инвестиционного    анализа используются различные методы оценки рисков проектов. По мнению ученых-практиков наиболее результативны и поэтому востребованы такие, как [1, с.175]:

• 1.    Анализ     альтернативных     сценариев

• 2.  Имитационное моделирование по методу

• 3.   Анализ чувствительности: метод вариации

реализации проекта.

Монте-Карло.

параметров и метод критических точек.

Каждый из этих методов имеет свои достоинства и недостатки и применяется в зависимости от специфики планирования инвестиционного проекта. В данной работе для расчета и анализа рисков инвестиционного проекта по выводу на рынок нового изделия был выбран метод Монте-Карло, с помощью которого можно не только смоделировать значения ключевых параметров проекта, но и произвести анализ разных сценариев реализации проекта и выполнить статистический анализ чувствительности проекта к изменению исходных данных.

Цель данного исследования ‒ оценка вероятной доходности проекта и целесообразности его инвестирования при различных сценариях планирования.

Объект исследования ‒ инвестиционный проект по производству мужских костюмов, артикул изделия JS-131773, модель 4222D/5073D, сорт 1 (рис. 1), планируемый к внедрению на ОАО «Знамя индустриализации», г. Витебск.

Инструментарий исследования – табличный процессор MS Excel.

Рисунок 1 ‒ Мужской костюм, артикул изделия JS-131773, модель 4222D/5073D

Источник: собственная разработка авторов.

Моделирование методом Монте-Карло используется для моделирования вероятности различных исходов в процессе, который не может быть легко предсказан из-за вмешательства случайных величин. Это метод, используется для понимания влияния риска и для оценки неопределённости проекта. Основой моделирования методом Монте-Карло является то, что вероятность различных исходов не может быть определена из-за присутствия случайных величин. Поэтому моделирование методом Монте-Карло фокусируется на постоянном повторении случайных выборок для достижения определенных результатов. При моделировании любого финансово-экономического процесса этим методом переменной, имеющую неопределенность, присваивается случайное значение. Затем модель запускается и выдается результат. Этот процесс повторяется снова и снова при присвоении рассматриваемой переменной множества различных    значений.    После    завершения моделирования результаты усредняются для дальнейшей оценки.

Процесс моделирования можно разделить на следующие этапы:

• 1.    Определение исходных данных.

• 2.    Проведение    компьютерной    имитации

• 3.    Оценка законов распределения вероятностей.

• 4.    Расчёт      основных      характеристик

• 5.    Проведение анализа полученных результатов и принятие решения.

ключевых параметров модели.

распределения исходных и выходных показателей.

В процессе предварительного анализа были выявлены три ключевых параметра проекта (переменные затраты V, объем выпуска Q, цена за единицу изделия P) и определены возможные границы их изменений. Прочие параметры проекта (постоянные затраты F, амортизация A, налог на прибыль T, норма дисконта r, срок проекта n, начальные инвестиции I0) считаются постоянными величинами (табл. 1).

Таблица 1 ‒ Исходные данные проекта по производству мужских костюмов

	Показатели
Сценарий	Минимум	Максимум	Наиболее вероятное значение
Переменные Затраты – V , тыс. руб.	75	80,52
Объем выпуска – Q , шт.	142	160
Цена за единицу изделия – P , руб.	120	144
Постоянные затраты – F , тыс. руб.			18,74
Амортизация – А , тыс. руб.			8
Налог на прибыль – Т, %			18 %
Норма дисконта – r , %			9,8 %
Срок реализации проекта – n , лет			1
Начальные инвестиции – I 0 , тыс. руб.			7200

Источник: калькуляция основных экономических показателей предприятия ОАО «Знамя индустриализации».

Для оценки эффективности проекта разработан алгоритм     инвестиционного     моделирования, включающий следующие этапы реализации:

Этап 1. Определение исходных данных.

Входными параметрами проекта являются переменные затраты V , количество Q , цена изделия P .

Выходным – величина чистой приведенной стоимости NPV . Для моделирования результатов инвестирования в проект исходные данные были занесены в электронную таблицу MS EXCEL (рис. 2).

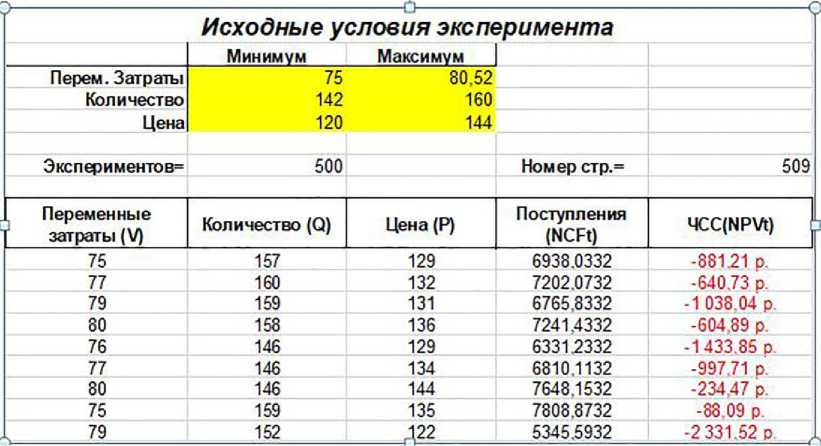
Рисунок 2 ‒ Исходные условия эксперимента

Источник: собственная разработка авторов.

Этап 2. Проведение компьютерной имитации ключевых параметров модели. Расчет значения чистой приведенной стоимости.

В соответствии с методом Монте-Карло для каждого из рассматриваемых факторов были рассчитаны следующие показатели: среднее значение, стандартное отклонение, коэффициент вариации, максимальное и минимальное значение. Для величины NPV было подсчитано количество случаев, когда NPV оказалось больше 0, сумма убытков

(если NPV < 0) и сумма доходов (если NPV > 0). Величина ожидаемой NPV составляет -1039,87 р., общее число отрицательных значений NPV в выборке составляет 423 из 500.

Исходя из полученных данных видно, что инвестиционный проект не выгоден и вероятность получения убытка при данных уровнях цен, объема и переменных затрат - 87 % (рис. 3).

Имитационный анализ (Метод Монте-Карло) Распределение с равными вероятностями

Начальные инвест.(1)	7200	Норма г	0.098
Пост.расходы (F)	18.74	Налог (Т)	0.18
Амортизация (А)	8	Срок (п)	1
Показатели	Переменные (V}	Количество (Q)	Цена(Р)	Поступления (NCFt)	NPV
Среднее значение	77.41	151.09	132.088	6763.82092	-1 039.87 р (
Стандарт. Отклонение	1.731444484	5.463140123	7.318487275	988,4552744	90 0.2324904
Коэф, вариации	0.022367194	0 036158185	0.055406148	0.146138593	-0.865714998
Минимум	75	142	120	4742,0732	-2 881.17 р
Максимум	80	160	144	8796.1532	811.07 р
Число случаев NPV<0					432
Сумма убытков					-542388.5588
Сумма доходов					22452.73005
Вероятность p(NPV<-X)			Веп.(Х)	Нормал. (X)	p(NPV<=X)
			0	1.155114561	0,8 759 78 242 .

Рисунок 3 ‒ Имитационный анализ на основе исходных данных

Источник: собственная разработка авторов.

Этап 3. Анализ результатов имитационного моделирования.

Проанализировав суммы убытков и прибыли, можно заметить, что ожидаемый чистый дисконтированный убыток -2881,17 р. при принятии проекта намного выше, чем ожидаемый дисконтированный доход 811 р. при инвестировании в проект, что также говорит о его нецелесообразности. Отношение этих двух величин говорит о рентабельности проекта, но при этом необходимо учитывать, что конкретное значение является частым случаем и для достоверности необходимо проведение ряда экспериментов с моделью.

Этап 4. Оценка законов распределения вероятностей.

Важнейшим этапом анализа является исследование зависимостей между ключевыми параметрами. Для определения взаимосвязи между переменными затратами V , ценой изделия P , количеством Q , потоком денежных платежей NCF и чистой приведенной стоимостью NPV были построены графики (рис. 4), с помощью которых было выявлено, что между параметрами NCF и NPV существует сильная корреляционная связь, а между V , P , Q , напротив, отсутствует корреляция как таковая. Этот вывод подтверждается и результатами корреляционного анализа.

На рисунке 4 представлена корреляционная матрица, рассчитанная средствами инструмента Анализ данных MS Excel.

Значения коэффициентов корреляции между переменными затратами V и количеством выпускаемых изделий Q (0,03544), ценой изделия Р и количеством Q (-0,0219), переменными затратами V и ценой изделия P (0,00055) достаточно близки к 0, что говорит об отсутствии линейной связи между переменными. В свою очередь величина показателя чистой приведенной стоимости NPV напрямую зависит от NCF (величины потока платежей). Кроме того, существует высокая корреляционная зависимость между ценой изделия P и NPV (R = 0,83), средняя между количеством Q и NPV (R = 0,52), слабая обратная между переменными затратами V и NPV (R = -0,16). По результатам анализа данных «Корреляция» можно сделать вывод, что увеличение или уменьшение величины переменных затратам V практически не повлияет на NPV, соответственно при дальнейшем анализе целесообразно изменять величины P и Q.

Этап 5. Расчёт основных характеристик распределения исходных и выходных показателей.

Для проведения более детального анализа с помощью инструмента «Описательная статистика» были рассчитаны широко используемые в практическом анализе характеристики распределений, представленные на рисунке 5. При этом значения определены сразу для нескольких переменных.

Характеристика «Уровень надежности» показывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности 95 %. Для данного проекта это означает, что с вероятностью 95 % величина математического ожидания NPV попадет в интервал от -1090,75-74,06 до -1090,75 + 74,06.

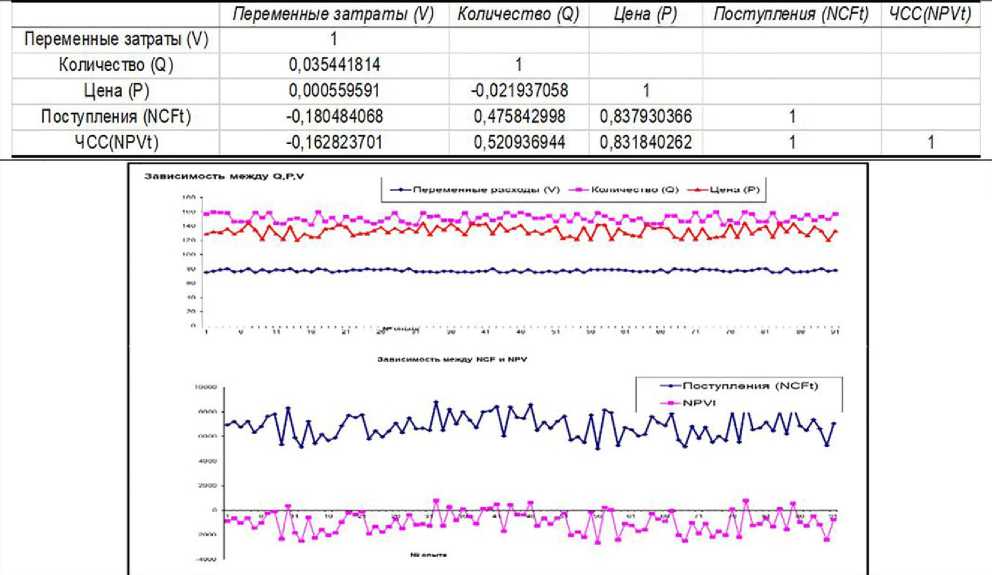
Рисунок 4 ‒ Корреляционная матрица и графический анализ зависимостей между ключевыми параметрами проекта

Источник: собственная разработка авторов.

—	Количество (Q)	' Цена (Р)	Поступления (NCFt)	— 4CC(NPVt)
Среднее	151,286	132,196	6782,27092	-1090,751985
Стандартная ошибка	0,23947255	0,330426287	43,2116617	37,69955249
Медиана	151	132	6808,8832	-1165,743898
Мода	146	122	6505,0732	-1750,497996
Стандартное отклонение	5,354 769005	7,38855639	966,2421298	842,9876208
Дисперсия выборки	28,6 735511	54,59076553	933623,8533	710628,1288
Эксцесс	-1,202984273	-1,189688465	-0,898252547	-0,7 726 20122
Асимметричность	-0,019670372	-0,048274503	-0,004930092	0,15 5361962
Интервал	18	24	4077,04	4002,91439
Минимум	142	120	4774,8732	-2970,789435
Максимум	160	144	8851,9132	1032,124954
Сумма	75643	66098	3391135,46	-545375,9927
Счет	500	500	500	500
Уровень надежноста(95,0%)	0,470498757	0,649198237	84,89922177	74,0694188

Рисунок 5 ‒ Инструмент анализа данных «Описательная статистика»

Источник: собственная разработка авторов.

Этап 5. Вывод и принятие решения.

В условиях неполной загрузки производственных мощностей, характерных в текущем периоде для рассматриваемого предприятия, решение о снятии с производства изделия, убыточного в результате расчетов чистой приведенной стоимости, не всегда оказывается верным. Для увеличения прибыльности проекта планово-экономический отдел предприятия может установить более высокую цену и объем производства.

Этап 6. Получение положительного показателя NPV.

Учитывая все обстоятельства, для получения положительной прибыли планово-экономический отдел ОАО «Знамя индустриализации» предложил изменить значения объём выпускаемой продукции Q и цены P в следующих направлениях: увеличить объём выпускаемой продукции на 15 % и цену изделия на 10 %, не изменяя значений остальных показателей.

В результате моделирования по этому сценарию шанс получить положительную величину чистой приведенной стоимости NPV составляет 92 %. Величина ожидаемой NPV составляет 1481,87 р. Общее число отрицательных значений NPV в выборке составляет 39 из 500, что говорит о целесообразности инвестирования в данный проект. Результаты вероятностного анализа представлены на рисунке 6.

Имитационный анализ (Метод Монте-Карло) Распределение с равными вероятностями
Начальные инвест Л1)	7200	Норма г	0.098
Пост, расходы (Е)	18.74	Налог (Т)	0,18
Амортизация (А)	8	Срок (п)	1
Показатели	Переменные (V)	Количество (Q)	Цена(Р)	Поступления (NCFt)	NPV
Среднее значение	77.55	174.082	144.44	9532.69688	1481.873297
Стандарт. Отклонение	1.701616878	6.246541123	7.715594598	1173.332567	1068.608896
Коэф, вариации	0.021942191	0.035882751	0,053417299	0,12308506	0 721120286
Минимум	75	163	132	7021.6732	-805.0335155
Максимум	80	184	158	12441,0532	4130,649545
Число случаев NPV<0					39
Сумма убытков					-9147.272495
Сумма доходов					750083.9209
Вероятность p(NPV<=X)			Вел.(Х)	Нормал. (X)	p(№V<=X)
			0	-1.386731201	0.082761871

Рисунок 6 ‒ Имитационный анализ при NPV > 0

Источник: собственная разработка авторов.

Таким образом, с вероятностью 95 % можно сказать, что величина NPV лежит в пределах от 1541,64 – 95,67 до 1541,64 + 95,67. Вероятность получить положительную прибыль = 92 %, инвестиции в данный проект целесообразны.

Этап 7. Расчет точки безубыточности.

Значение этого показателя имеет огромную значимость для предприятия, так как именно точка безубыточности определяет количество продукции, при котором выручка от реализации продукции равна затратам на её производство. В случае превышения точки безубыточности предприятие получает прибыль, если точка безубыточности не достигнута, то предприятие несет убытки.

Расчет точки безубыточности даёт возможность:

• -    определить оптимальную стоимость реализации производимой продукции;

• -    вычислить срок, в течение которого будет окупаться новый проект. А именно – определить момент, когда полученные доходы превысят издержки производства;

• -    проводить анализ финансового состояния предприятия;

В результате моделирования значения точки безубыточности было принято решение увеличить объём выпускаемой продукции и цену на 5 % (до значений 149 – 168 шт., 129 – 151 руб.).

После изменения объёма, значение NPV ≈ 0 белорусских рублей. Шанс получить положительную прибыль (убыток) составляет 50 %. Общее число отрицательных значений NPV в выборке составляет 247 из 500, что составляет около половины от общего числа симуляций, сумма доходов и убытков также приблизительно равны между собой, это говорит о том, что проект не приносит ни прибыли, ни убытков (рис. 7).

При помощи инструмента анализа данных «Описательная статистика» удалось выяснить, что среднее значение NPV составляет 5 и с вероятностью 95 % можно сказать, что величина NPV лежит в пределах от 5,1966 – 95,7343 до 5,1966 + 95,7343.

Для руководства предприятия точка безубыточности является важным ориентиром в анализе, так как она показывает уровень продаж, ниже которого предприятие будет нести убытки. По этой причине ее можно рассматривать как минимально приемлемый уровень продаж продукции или услуг.

ЗАКЛЮЧЕНИЕ

Большинство предварительных оценок начинаются с базового сценария. Однако принятие каких-либо решений на основе базового сценария ошибочно, а создание прогноза только с одним исходом недостаточно, поскольку в нем ничего не говорится о любых других возможных результатах и о весьма реальной вероятности того, что фактическая будущая стоимость будет отличаться от прогнозируемой. Невозможно застраховаться от негативного события, если факторы и вероятность этих событий не рассчитаны заранее.

Имитационный анализ (Метод Монте-Карло) распределение с равными еероятнсстями

Купальные waecr.ft) Лмг.рзехэды (F)		7203       Норма г		0,098
		18.74 8	Налое (Т)	0.18
Аморпззцгя (А)			Срок (п)	1
Показатели		Переменные (V)	Количество (Q)	Поступленда Цена (Р)      (^^	NPV
Среднее зжмен'е		77,684	153,738	138,536      7907,00424	1,279
Стандарт. Отспонеч-е		1,66857544	5.631545438	7,518823312    1017.796377	926.955
Коэф, взргзцж		0,02147901	0,035477431	0,054273426   0,128720859	724,802
У wiwyv		75	149	126         5728,5332	-1982,757
Масаями		80	168	151         10180.3132	2071.638
Чиапо случаев hFV<0					247
Cyv\a убытков					-195073,597
CyVMB доходов					195718051
пероятюрть pf№Y<=X)				Эел.(Х)       Ноомал. (X)	p'M=V<=X}
				0        -0.001379687	0.499449585

Рисунок 7 ‒ Имитационный анализ при NPV≈0

Источник: собственная разработка авторов.

Имитационное моделирование и анализ по методу Монте-Карло полезен, потому что многие инвестиционные и деловые решения принимаются на основе одного результата. Другими словами, многие аналитики выводят один возможный сценарий, а затем сравнивают этот результат с различными препятствиями на его пути, чтобы решить, следует ли продолжать.

Модель Монте-Карло позволяет исследователям из самых разных областей провести несколько испытаний и, таким образом, определить все потенциальные результаты события или решения. В финансовой отрасли решение обычно связано с инвестициями. При объединении все отдельные испытания создают распределения вероятностей или оценку риска для данной инвестиции или события.

Однако следует отметить, что использование этого метода требует от исполнителя высокого уровня профессионализма, владения основами экономико-математического моделирования, бизнес-аналитики и информационных технологий, что в условиях четвертой промышленной революции и диджитализации экономики является неотъемлиемым требованием к профессиональной подготовке специалиста любого профиля.