Имитационное моделирование при проектировании регенерационных систем жизнеобеспечения пилотируемого космического аппарата

По мере развития пилотируемой космонавтики все бóльшую актуальность приобретает задача разработки перспективных систем пилотируемого космического аппарата (ПКА), основанных на процессах регенерации продуктов жизнедеятельности экипажа [1].

При анализе свойств регенерационной системы жизнеобеспечения как объекта проектирования необходимо учитывать, что она является сложной функциональной системой и характеризуется наличием общесистемных свойств, а также техническими требованиями, такими как показатели назначения, надежности, эргономичности и др.

Номенклатура показателей (технических требований) закладывается на этапе проектирования (модернизации) ПКА и окончательно формируется при разработке конструкторской документации системы. Далее, на этапе производства, эти показатели находят свое воплощение в конструкции системы. Первоочередной интерес представляют показатели назначения (ПН), так как именно они обусловливают пригодность продукции к выполнению определенных требований в соответствии с ее назначением, а также определяют соответствие системы ее функциональному назначению в составе ПКА и характеризуют способность системы эффективно выполнять свою функцию [2].

Для регенерационных систем жизнеобеспечения ПКА можно выделить типовой набор ПН, например, таких как:

• •    производительность системы (количество получаемых воды и кислорода);

• •    количество удаляемого диоксида углерода, газообразных микропримесей и т. д.;

• •    качество выходного продукта (электрическая проводимость полученной воды и содержание в ней свободного газа, степень концентрации удаленного из атмосферы ПКА и собранного диоксида углерода и т. д.);

• •    температура нагрева внешних поверхностей оборудования для обеспечения безопасности экипажа ПКА.

Проектирование и наземная экспериментальная отработка — важнейшие этапы создания систем регенерационного типа, так как последующие летные испытания, совмещенные со штатной эксплуатацией, не позволяют использовать их результаты для устранения последствий ошибочных конструкторских решений. В связи с этим важной задачей в совершенствовании процесса разработки данных систем является обеспечение достоверной оценки ПН систем регенерационного типа на этапе проектирования.

Структура и назначение имитационной модели функционирования интегрированной регенерационной системы обеспечения газового состава ПКА

На стадии проектирования использование конструкторско-технологических макетов для оценки и анализа ПН разрабатываемой системы является экономически невыгодным в силу сложности систем регенерационного типа. Более рациональным подходом является применение виртуальных имитаторов разрабатываемых регенерационных систем жизнеобеспечения и взаимосвязанных с ними других систем ПКА, объединенных в единую имитационную модель [3].

Исследования проводились на вновь разрабатываемой РКК «Энергия» и АО «НИИхиммаш» системе переработки диоксида углерода — части интегрированной регенерационной системы обеспечения газового состава ПКА для длительных автономных космических полетов, структура имитационной модели которой приведена на рис. 1.

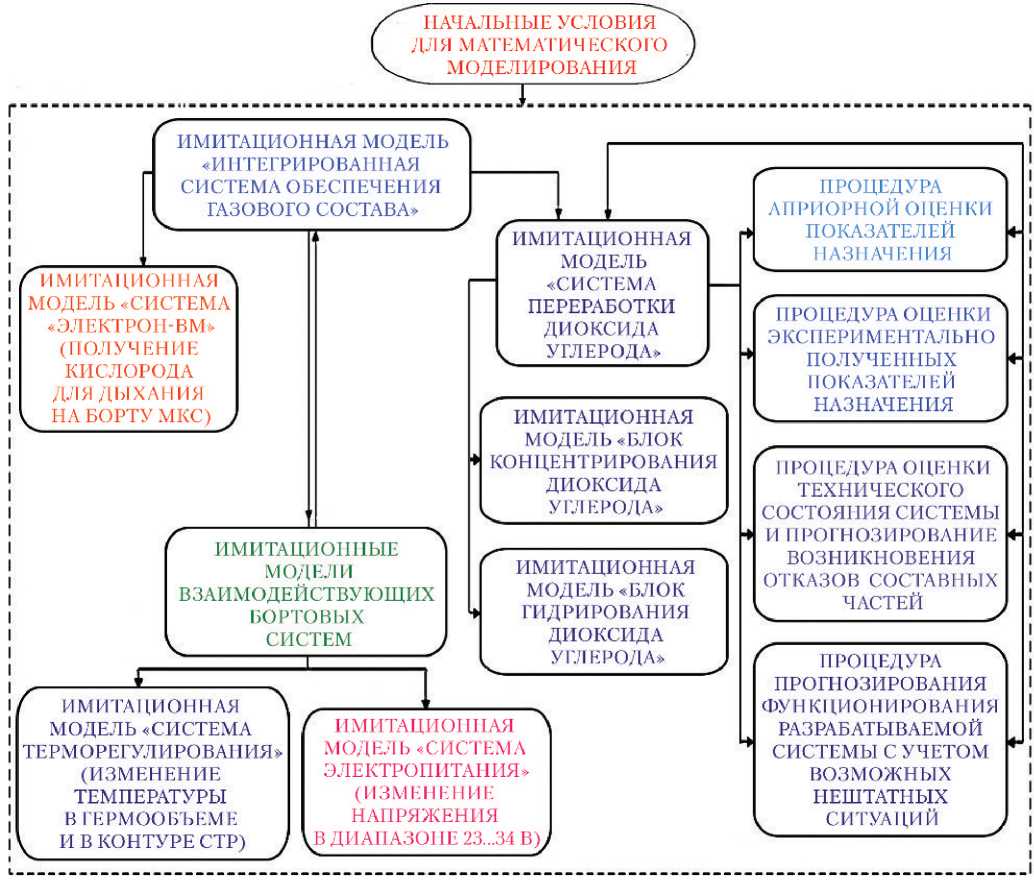
Рис. 1. Структура имитационной модели интегрированной регенерационной системы обеспечения газового состава

Рассматриваемая система, как и любая перспективная регенерационная система жизнеобеспечения ПКА для длительных автономных полетов, характеризуется сложными взаимосвязями между входящими в нее блоками и сложным взаимодействием при их функционировании [4].

Основным блоком системы переработки диоксида углерода, определяющим ее производительность по целевому продукту, является блок гидрирования диоксида углерода, осуществляющий получение воды по реакции Сабатье (рис. 2).

Основным агрегатом блока является реактор, именно он определяет степень извлечения целевого продукта. Выбор оптимальных режимов функционирования и конструктивных решений при его проектировании может быть произведен на основе имитационного моделирования химических и тепловых процессов.

Рис. 2. Структурная схема блока гидрирования

Имитационная модельреактора гидрирования диоксида углерода

параметры модели), являются независимыми величинами [6].

Схема реактора представлена на рис. 3.

Имитационная модель функционирования реактора гидрирования, предназначенная для выбора его конструктивного исполнения и оптимальных выходных параметров функционирования, позволяет проводить анализ технических требований, определяемых техническим заданием, и оценку показателей назначения системы.

При разработке имитационной модели

и проведении вычислительных эксперимен тов были приняты следующие допущения:

-

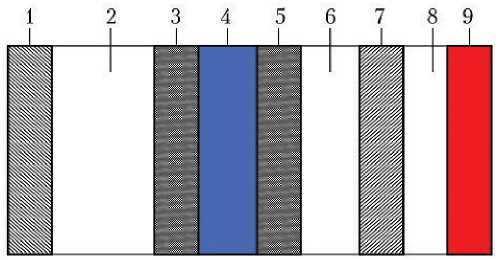
Рис. 3. Схема реактора гидрирования диоксида углерода по реакции Сабатье: 1 — оболочка; 2 — полость; 3 — стенка 3; 4 — катализатор; 5 — стенка 2; 6 — рекуператор; 7 — стенка 1; 8 — зазор; 9 — нагреватель

• •    реактор представляется в идеального вытеснения» [5];

• •    уравнения переноса уравнениями материального

виде «модели

заменяются и теплового

балансов при задании на границах раздела конструктивных элементов граничных условий третьего рода [5];

• факторы, влияющие на функционирование исследуемой системы (входные

Формализованное описание процессов, происходящих в реакторе, может быть

записано в форме системы дифференци альных уравнений первого порядка с част ными производными:

-

-

dT

( Cpm ) наг =	н аг = N – α F ( T – T ), наг       1 1 наг       1
( C p ρ V ) 1	∂ T 1 ∂ τ 1   = – ( C p G ) 1 + α 1 F 1 ( T наг – T 1 ) – α 1 F 2 ( T 1 – T ст1 ),
( C p ρ V ) ст1	∂ T ∂ τ с т 1 = – α 2 F 3 ( T ст1 – T 2 ) + α 1 F 2 ( T 1 – T ст1 ),
( C p ρ V ) 2	∂ T             ∂ T 2 = ( CG )       2 + α F ( T – T ) – α F ( T – T ), ∂τ            p 2     ∂ x       2 3 ст1     2       2 4   2     ст2
( C p Р VU	∂ T дт - a , F , ( T, — T „) — k , F , ( Tс - T, ),
( C p Р V ) к "	∂ Tr                ∂ Tr я - - ( CG )    я + kF ( T , - T ) - k^Fp. ( T - T ) дТ              P r д X         2 5 cm2 T 3 6 r     CT3
( C p ρ V ) ст3	∂ T с т3 = kF ( T – T ) – σε F ( T 4 – T 4 ) – α F ( T – ∂τ           3 6 r      ст3         пр 7 ст3      об       3 7 ст3
( C p ρ V ) 3	∂ T            ∂ T 3 = ( CG )      3 + α F ( T – T ) – α F ( T – T ), ∂τ            p 3    ∂ x         3 7 ст3     3       3 8   3     об ,
( Cp ρ V ) об	∂ T о б = σε F ( T 4 – T 4 ) + α F ( T – T ) – α F ( T – пр 7 ст3      об       3 8   3      об       4 9 об

+ ∆ H_RW ( X, T ) V_k ,

T 3 ),

^T окр^),

∂ X

C

⁰ ∂τ

W ( X, T_r ) =

^{C 0 V вх}

V k

^{S уд ρ к} 3600 V µ

T

r

T вх

∂ X

+ νπ W ( X, T ), ∂ х               ^r

K ₁ ( α – 4 X ) (1 – X ) p

s(K ₂ ( α – 4 X ) + 1 – X + ( s/p ) K ₃ )

( β + X ) ( γ + 2 X ) ² s ²

1 –

K (1 – X )( α – 4 X ) ⁴ p ²

.

В системе уравнений использованы следующие обозначения: Т _наг — температуры поверхности нагревательного элемента; Т ₁ — температура в зазоре между нагревателем и стенкой 1; Т _ст1 — температура внутренней стенки рекуператора; Т ₂ — температура газа в рекуператоре; Т _ст2 — температура стенки между рекуператором и реакционной зоной; Т_r — температура катализатора; Т _ст3 — температура внешней стенки реакционной зоны; Т ₃ — температура газа в теплоизолирующей полости; Т _об — температура оболочки теплоизолирующей капсулы; Т _окр — температура окружающей среды; С_р — массовые теплоемкости соответствующих элементов, Дж/кг/К; ρ — плотности соответствующих элементов, кг/м ³ ; V — объемы соответствующих элементов, м ³ ; m_i — массы соответствующих элементов, кг; F_i — площади поверхности соответствующих элементов, м ² ; N _наг — мощность нагревателя, Вт; α _i — коэффициент теплопроводности стенки, Вт/(м ² К); k_i — коэффициент теплопередачи, Вт/(м ² К); G — массовый расход газов, кг/с; Δ H_R — энтальпия, Дж/моль; W — скорость реакции, моль/с; Х — количество прореагировавшего вещества; S _уд — удельная площадь поверхности катализатора, м ² /г; К _1,2,3 — кинетические коэффициенты; ε_пр — приведенная степень черноты системы стенок; A , β , γ , δ — соотношения газов, служащие для определения идеального приведенного объема s простого и эталонного веществ; s = 1 + A + β + γ + δ – 2 X ;

A = C 0 H / C 0 CO ; β = C 0 CH / C 0 CO ; γ = C _{0 H2O} ² / C _{0 CO} ² ₂ ; δ = C _{0 N2} ⁴/ C _{0 CO2} ;²

K ₁ = 1,03 × 10 ⁹ exp(–10 320/ T_r );

K ₂ = 7,64 × 10 ^–2 exp(2 620/ T_r );

K ₃ = 2,02 × 10 ⁴ exp(–5 300/ T_r ).

В ходе имитационного моделирования были определены наиболее значимые факторы (входные параметры модели), варьирование которых приводит к изменению основного показателя назначения — «выход по воде», это:

• •    объемные соотношения исходных реагентов СО ₂ и Н ₂ ;

• •    объемная скорость подачи газовой смеси СО ₂ и Н ₂ в реактор;

• •    температура протекания процесса гидрирования, определяемая конструкцией реактора.

Математическое описание с достаточной степенью точности отражает структуру и конструктивные особенности агрегата, а также характерные особенности осуществления процессов теплового и массового обменов в конструктивных элементах.

Анализ результатоввычислительных экспериментов

По результатам моделирования выбраны конструктивные параметры внешней теплоизоляции, геометрические размеры реакционной зоны и рекуператора, а также определены оптимальные значения входных параметров БГДУ. Варьировались следующие параметры:

• •    присутствие/отсутствие внутреннего рекуператора, отделяющего катализатор от нагревателя;

• •    размер канала рекуператора;

• •    геометрические размеры полости с катализатором, высота слоя;

• •    материал и расположение внешней теплоизоляции;

• •    давление углекислого газа в защитной капсуле;

• •    расход реагентов;

• •    допустимое содержание неинертных примесей в газах.

На основе полученных данных при проведении вычислительных экспериментов в АО «НИИхиммаш» с использованием имитационной модели был разработан, а затем изготовлен экспериментальный реактор гидрирования, на котором с середины 2015 г. было наработано более 800 ч на различных режимах; испытания подтвердили адекватность имитационной модели.

Зависимости показателя назначения «выход по воде» от температуры протекания процесса и соотношения реагентов, полученные при проведении вычислительных экспериментов с использованием имитационной модели (обозначены линиями) и усредненные значения, полученные на экспериментальном реакторе (обозначены маркерами), показаны на графиках рис. 4 и 5.

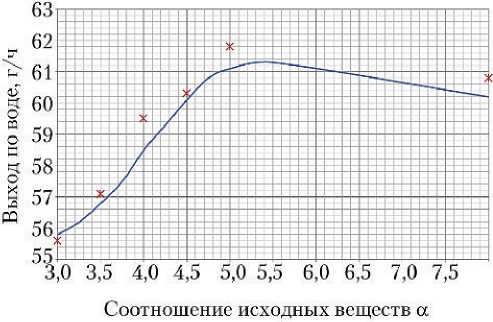
Рис. 4. Зависимость выхода по воде от соотношения реагентов при подаче СО 2 : ■ — результаты моделирования;

— экспериментальные значения

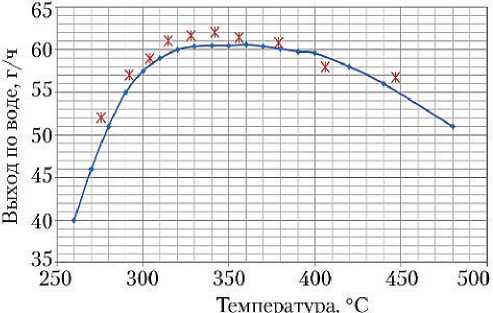
Рис. 5. Зависимость выхода по воде от температуры реакции (определяющий критерий: параметры теплоизоляции): ■ — результаты моделирования; X — экспериментальные значения

Таким образом, определены оптимальные входные параметры функционирования реактора:

• •    соотношение исходных компонентов реакции Сабатье Н ₂ : СО ₂ должно быть (5÷5,5) : 1;

• •    температура протекания реакции 320...360 ° С;

• •    частичная теплоизоляция, обеспечивающая более полный профиль температур.

При этих значениях входных параметров достигается максимальный выход по воде 61–62 г/ч при расходе СО ₂ 40 л/мин.

Выводы

Использование метода имитационного моделирования позволяет:

• 1.    Проводить анализ соответствия разрабатываемой системы своему функциональному назначению на стадии проектирования.

• 2.    Интенсифицировать процесс проектирования сложных регенерационных систем

• 3.    Прогнозировать функционирование регенерационных систем жизнеобеспечения пилотируемого космического аппарата на всех этапах их разработки.

пилотируемого космического аппарата, так как отсутствует необходимость изготавливать конструкторско-технологические макеты и проводить испытания для выбора конструктивных характеристик системы и определения оптимальных значений факторов, влияющих на ее функционирование.