Имитационное моделирование процесса высокоскоростного трения и изнашивания

Трение представляет собой совокупность одновременно протекающих процессов. При построении математических моделей трения основными из этих процессов принято учитывать: тепловыделение в зоне контакта; деформирование и изнашивание поверхностных слоев контактной пары; физико-химические процессы взаимодействия трущихся тел друг с другом и средой; структурные и фазовые превращения в трущихся телах. Перечисленные процессы непосредственно связаны с трением потому, что проходят при температуре, которая достигается в результате разогрева от трения. Так при нагреве закаленных сплавов или мелкодисперсных структурных составляющих, в частности наноструктур могут происходить релаксационные процессы, а нагрев до температур, близких к температуре плавления одного из элементов контактной пары приводит к деструкции материала поверхности или к плавлению, сопровождающимся абляцией материала.

Как правило, трение поверхностное явление. В условиях кратковременных процессов высокоскоростного трения материалы контактирующих пар не успевают прогреваться на всю глубину, а поэтому в теплопоглощении участвуют тонкие поверхностные слои. Скорость распространения теплоты в результате теплопроводности в твердых телах является бесконечно большой (например, у алюминия она приблизительно равна 3000 м/с). Глубина поверхностного слоя материала участвующего в трении составляет всего несколько десятков микрометров [1, 2]. Однако условия, формирования данного слоя зависят от физических свойств материалов пары, в частности, теплофизических и механических. Так при трении материалов с относительно малой теплопроводностью (пластмасс, керамики и др.) в зоне трения концентрируется большое количество тепловой энергии, приводящее к большим температурам, а при трении тел с большой теплопроводностью, объем нагретой зоны – значительно больше. При рассмотрении кратковременных процессов теплопередачи обычно анализируют размер областей, в которых сосредоточено основное количество теплоты.

В общем случае глубину прогретой зоны при трении 5 следует вычислять согласно Ю.Н. Дрозд ов у [2] по уравнению:

• 5 = kVai, (1)

где: k – некоторый числовой коэффициент, выбор которого в каждом конкретном случае зависит от того, какое физическое обоснование положено в основу понятия толщины приповерхностного теплового слоя; а - коэффициент температуропроводности (м2/с); t - время.

Как правило, под толщиной теплового слоя по- нимают толщину приповерхностного слоя, в котором сосредоточено основное количество теплоты, поглощенной в данный момент вре- мени рассматриваемым элементом пары тре-

ния. В табл. 1 приведены значения коэффици- ента k при разных отношениях температур

T(8,t) T(O,t) ^,

вычисленные для случая нагрева полуог- раниченного тела постоянным тепловым потоком, направленным перпендикулярно к его плоской границе.

Таблица 1. Значения коэффициента k

T(8,t) T(O,t)	0,01	0,05	0,1	0,2	0,4	0,6
k	3,2	2,4	1,94	1,44	0,9	0,54

В табл. 2 приведены значения эффективных толщин прогретого слоя 5, для разных времен действия теплового потока и различных по природе материалов, на поверхности которых этот поток действует. Из табл. 2. следует, что поверхностные слои металлических пар прогреваются на глубину 5 , на порядок большую, чем пластиковые. За одно и то же время нагрева самый теплопроводный, в соответствии с табл. 2, металл – медь прогревается на глубину, в 4 раза большую, по сравнению с глубиной прогрева одного из наименее теплопроводных металлов висмута и в 24,4 раза большую, чем полипропилен и в 55 раз большую, чем полиамид.

Таблица 2. Глубина прогрева

Материал образцов	а 104, м2/с	Глубина слоя 5, мм при t, с
		10 -5	10 -4	10 -3	10 -2	10 -1	1	10
Армко-железо	0,08	0,018	0,057	0,18	0,57	1,8	5,7	18
Сталь 45	0,07	0,017	0,053	0,17	0,53	1,7	5,3	17
Медь	1,0	0,061	0,19	0,61	1,9	6,1	19,	62
Алюминий	0,82	0,056	0,175	0,56	1,75	5,6	17,	56
Висмут	0,06	0,015	0,048	0,15	0,48	1,5	4,8	15
Цинк	0,3	0,034	0,106	0,34	1,06	3,4	11,	34
Молибден	0,46	0,04	0,130	0,41	1,30	4,1	13,	41
Вольфрам	0,47	0,042	0,134	0,42	1,34	4,2	13,	42
Полипропилен	0,002	0,002	0,004	0,02	0,04	0,2	0,4	2,
Полиамид	0,001	0,001	0,003	0,01	0,03	0,1	0,3	1,

Огромное влияние на процесс переноса вещества в контактном зазоре имеют давление p (Па) и скорость скольжения v с (м/с). Существует критическое значение фактора pv с (эта величина часто применяется в практической трибологии [2]) выше которого материал становится неработоспособным. Допускаемые, например, для полиамидов давления при постоянном контакте во времени составляют [ р ] = 5,0 ^ 7,0 МПа, а допускаемые скорости лежат в пределах [ v _с] = 0,5 ^ 0,6 м/с [3]. При расчетах полимерных узлов трения обычно берут [ р ] < 3,0 МПа, а [ v _с] < 0,2 м/с, фактор [ pv _с] = 2,5 ^ 4,2 МПа м/ с.

У некоторых материалов поверхностные слои сильно адсорбируют воду. Это явление может способствовать понижению коэффициента трения. Поскольку после переноса, когда трение происходит по существу между двумя поверхностями полимера, эта адсорбированная вода играет роль смазки и тем самым обеспечивается низкое трение материалов. Наличие адсорбированной воды, однако, может нести отрицательные воздействие на износостойкость, способствовать деструкции поверхности за счет поверхностных явлений, известных как эффект Ребиндера. Этим, возможно, объясняться малая, по сравнению с полипропиленом, стойкость полиамидов [4], имеющих близкие механические свойства.

Следует упомянуть, что реальные поверхности никогда не бывают абсолютно гладкими, т.е. они всегда обладают определенной шероховатостью. Контакт шероховатостей образует пятна контакта, которые имеют весьма малые размеры (от нанометров до нескольких микрометров). Поэтому при соприкосновении шероховатостей под ними возникают большие контактные давления о_. Эти давления всегда к очень велики, даже при малых общих нагрузках, так как общая площадь пятен контакта мала. Изнашивание полимера происходит в том случае, когда интенсивности напряжений оi, вызываемые контактными давлениями p в поверхностном слое превосходят его прочность. Основной механизм изнашивания определяется по соотношению между действующим напряжением и прочностью при данной температуре.

Если интенсивности напряжений о i ниже предела текучести о _т , то наиболее вероятно усталостное изнашивание. Если напряжения о i превышают предел текучести, но не превосходят предела прочности о _в , то наиболее вероятно пластическое деформирование (срез материала касательной силой). Если напряжения о i превышают предел прочности о _в , то преобладающим становится абразивное изнашивание, и частицы износа образуются сразу без какого-либо инкубационного периода.

Многие фундаментальные аспекты фрикционного взаимодействия остаются все еще не выясненными. Здесь в первую очередь следует сказать о формировании поверхностных контактных слоев. Известно, что тонкие поверхностные слои имеют иные физические свойства, чем материал объема. Это относится и к механическим свойствам. Не менее сложные задачи возникают и при изучении разрушения поверхностных слоев. Разрушение при фрикционном взаимодействии начинается сразу в большом количестве микрообъемов. Кроме того, область контакта практически недоступна для исследований в процессе фрикционного взаимодействия. Поэтому вопросы образования приповерхностных трещин, их объединения и эволюции во времени очень сложны для изуче- ния. Большое влияние на фрикционное взаимодействие оказывает трансформация энергии трения, которая имеет место в контактном зазоре. Часть энергии идет на деструктивные процессы, а часть на прямой нагрев материала, что вызывает изменение механических свойств материалов поверхностных слоев элементов фрикционной пары и что, в дальнейшем, также сказывается на динамике процесса трения.

Для прогнозирования изнашивания абразивных пар при контактном взаимодействии принято [2] рассчитывать характерные удельные величины износа. К которым относят: , dl

Ih = — - интенсивность линейного изнашивания; /у = d~ — интенсивность объемного изна- dG шивания; I, = G ds

–

интенсивность массового

dV изнашивания; Iw = — - интенсивность энерге тического изнашивания.

Здесь: l,V,G - линейный, объемный, массовый износ, соответственно; 5 - путь трения; А - работа сил трения, которая может быть выражена] зависимостью:

t

А = / р • F J q ^P At,             (2)

где: F - площадь контакта; / тр - коэффициент кулоновского трения; t - время.

Для примера – у современных машин интенсивность линейного изнашивания трущихся пар I_h , обеспечивающая их требуемый ресурс, составляет величину 10^-6 ÷ 10^-12 м/с.

Очевидно, что или другая характеристика абразивного изнашивания должна применяться в зависимости от условий, определяе- мых адекватностью эксперимента натурным условиям работы контактной пары.

Текущее значение коэффициента трения зависит от условий взаимодействия, в частности во многих происходящих процессах большой степени от скорости скольжения v_c . Так в результате экспериментальных исследований, описанных в работе [5] определена зависимость для / тр в виде:

_{f = f ⋅} 1-α 1 ⋅ v с ^{тр 0} 1+α ₂ ⋅ v_с ^,

где коэффициенты α1 и α2 могут учитывать пе- речисленные условия процесса (разгон, торможение, контактное давление, материал и др.)

Обычно большинством этих условий пренебрегают, не придавая большой значимости точности учета процесса трения. Так в работах [5, 6] приводятся значения коэффициентов α1 и α2 – 0,003 и 0,072 для стальной пары и 0,0009 и 0,0098 для пары медь-сталь соответственно, определенные на газодинамических установках. При значении этих коэффициентов αi ко- эффициент трения fтр быстро падает с ростом скорости скольжения.

Считается, что трение полимеров подчиняется несколько другим законам, чем трение металлов. Так на основании большого количества экспериментальных работ следует, что сила трения для полимеров пропорциональна площади фактического контакта, а у металлов сила трения пропорциональна нагрузке. Установлено [3], что у полимеров коэффициент кулоновского трения f _тр при увеличении нагрузки незначительно падает. Особенности такого отличия, очевидно, связаны со значительным отличием физических свойств полимеров и металлов. Прежде всего теплофизических (табл. 3) и механических. Особенности строения и структуры полимеров, приводят к значительно выраженной резкой зависимости их физико-механических свойств от температуры.

Трение при большом тепловыделении и относительно малом отводе тепла может происходить при плавлении материала одной из трущихся пар вблизи ее поверхности. В этих условиях фрикционное поведение пар трения определяется характером процесса плавления, свойствами и толщиной расплавленной пленки.

Таким образом, изучение вопросов контактного взаимодействия твердых тел при высоких скоростях скольжения показывает, что повышение износостойкости трущихся пар тесно связано с необходимостью анализа процессов тепловыделения, распределения теплоты в области контактных температур и температурных полей, механических и адгезионных свойств нагретых поверхностных слоев, процессов, связанных с оплавлением поверхностей трения.

Наиболее известные методы исследования процесса высокоскоростного трения [1 – 5] основаны на математическом анализе теплофизических процессов, связанных с нагреванием материала при высоких скоростях скольжения, размягчением и плавлением его в зоне фактического контакта. При этом некоторые параметры процессов могут быть определены экспериментально, например: αтп - коэффициент распределения тепловых потоков между контр- телами трущейся пары; σs (Т) - характеристики пластичности материалов контртел в зависимости от их температуры; Ij - интенсивность абразивного изнашивания и др.

Таким образом, можно констатировать следующие особенности, которые необходимо учитывать при построении общей имитационной модели высокоскоростного трения.

Таблица 3. Теплофизические характеристики материалов пар трения

Й s s 5 й ^ Л о н S о § 2 ч 2 — с В н и £ S' Н ^ о о ё 1н ч » ® < 0,6 ÷0,8 2120 0,74 1,62 - о 2 0,4÷0,6 2000 1,28 0,84 - Ж о о и 0,5÷0,7 1600 0,84 0,80 - S 2 « 0,2÷ 0,35 2800 164 0,884 ЧО Л S о" и 0,12÷ 0,20 7830 53,6 0,465 S х 0,15÷ 0,25 7900 16 0,502 о ч о с 0,22÷ 0,35 1010÷ 1360 0,184 1,28 S s о 0,20÷ 0,30 900÷ 955 0,184 1,26 40 физических характеристик от основного материала.

• 3.    Механические свойства твердых тел являются зависимыми от многих факторов, основным из которых, при трении в указанных условиях, является температура.

• 4.    Трение при большом тепловыделении может происходить при плавлении материала одной из трущихся пар вблизи ее поверхности. В этих условиях фрикционное поведение пар трения определяется характером процесса плавления, свойствами и толщиной расплавленной пленки.

• 5.    Начальные значения коэффициента трения и интенсивности изнашивания (в заранее известных условиях, например при установленной скорости скольжения и температуре контакта) являются зависимыми от многих факторов, определяющих взаимодействие контактной пары. Они могут быть определены экспериментально.

С учетом перечисленных особенностей, связанных с многофакторностью, исследование процесса высокоскоростного трения связано как с необходимостью проведения теплофизических исследований, так и с необходимостью точного учета условий взаимодействия, анализа присутствия и влияния различных факторов на условия и характеристики процесса. Важное значение при определении начальных количественных характеристик процесса трения и изнашивания при этом следует придавать учету подобия экспериментальных и реальных условий моделирования и учету значимых процессов, происходящих при трении, определяющих, в конечном счете, изменение значений этих характеристик.

Так в работе [5] была построена модель изменения характеристик процесса высокоскоростного трения на основании падения механических свойств от температуры [1], выделяемой при трении (рис. 2).

Математическую модель трения можно строить на базе решения тепловой задачи при граничных условиях 2-го рода (если задан тепловой поток q 1 на границе контакта внутрь рассматриваемого элемента с индексом "1" по координате r ):

q =^а тп • / • v • p .                 (4)

Для определения температуры поверхности трения можно воспользоваться дифференциальным уравнением теплопроводности для одномерного теплового потока в изнаши-

_ -               .   9q     92 T ваемьш скользящий элемент —1 = a--- [6],

5 t     ¹ 5 r ²

решение которого при заданных граничных условиях второго рода:       при r = ro^®T(”’t= 0, T(co,t) = T; при о r                    0

r = 0^T(0,0)= To, T(0,t)= Tn,

где: а п - коэффициент теплоотдачи зависящий

q i =

- ^X i

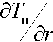
, может быть получено в виде

профиля температурного поля по длине r вор-

сины щетки:

T=T ¹0

"/

а для поверхности контакта

_T        q1 • -V 3 ' a • t

T = ‘ 0 ⁺ 'x ^.

Выражение (5) характеризует распределение температуры по глубине скользящего элемента близкое к экспоненциальному. Для расчета температуры при этом требуется опре-

деление теплового потока из решения уравнения теплового баланса на границе контакта и толщины теплового слоя. Пример такого распределения получен в работе [7] при анализе

трения полиамидных щеток коммунальных машин (рис. 1).

Выражения (4 и 5) справедливы для

кратковременно протекающих процессов, когда любое из контртел можно рассматривать как полуограниченное пространство. Для длительно протекающих процессов необходимо учитывать теплообмен с окружающей средой. Как правило, температура окружающей среды Т_о ниже, чем температура контртела, подвергающейся тепловому воздействию со стороны фрикционного контакта. При этом для установившихся процессов распределение температуры будет зависеть от геометрии контртел.

от скорости воздушного потока и в соответствии с уравнением [8]

ап = 7,15 и0’78 ;                       (8)

Т п - температура боковой поверхности стержня.

При условии постоянной температуры на поверхности контакта (установившийся процесс) в зоне конвективного теплообмена

распределение температуры по длине стержня можно выразить формулой, вытекающей из известного решения Римана для задачи с гранич-

ными условиями III-го рода, которое для постоянной температуры контактной торцевой поверхности преобразуется [6] к виду

Г Го _ 1 [g-mr

Т п -Г о    2

— егМ2Т51 —mVot) +

где

е ^mrerfc ( 25 + ^Vot^j, (9) обозначено:™ = J^4aп^ в ; trf^^

Г

^^ /( ) ^2V “^ e ^s2ds - интеграл вероятности Гаусса; erfc(z) = 1 — erf(z), который может быть вычислен суммой бесконечного ряда до заданной наперед ошибке, определяемой по значению последнего взятого члена ряда:еrf(z) « ^[l- £l ₊ £i — £l ₊ _j.

Vn 1!3   2!5   3!7

На рис. 2 приведена графическая зависимость изменения температуры контактной

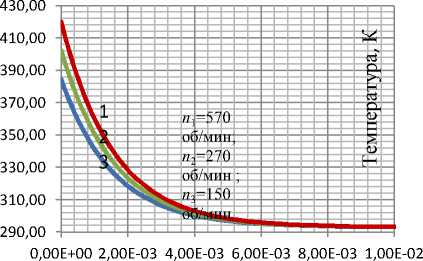
поверхности Т п лески полиамидной щетки коммунальной машины во времени (D = 550 мм , и = 270 об / мин ) при ширинах контакта Н к : 1 й- Н к =70 мм; 2 - Н к =150 мм.

Здесь явно выражены участки увеличе-

Расстояние , м

Рисунок 1. Распределение температуры по длине лески щеточного ворса при различных частотах вращения n (при n =570 об/мин температура в контакте близка к температуре плавления материала лески)

ния и снижения температуры в соответствии с подводом тепла (при контакте) и отводом тепла (после окончания контакта). Из графиков вид- но, что в течение нескольких секунд с момента начала рабочего процесса наступает термодинамическое «равновесие». При этом температура в контакте колеблется между двумя предельными значениями, соответственно Тв -верхним пределом и Тн - нижним пределом. При увеличении интенсивности тепловыделения в контакте (с увеличением времени контак та и при уменьшении времени теплоотдачи в окружающую среду), например с увеличением ширины контакта – верхний предел температуры Тв достигает значения, близкого к темпера- туре плавления, т.е. соответствует температуре, при которой теряются прочностные свойства материалом лески. В этом случае будет проис-

Частным случаем установившегося процесса рассмотрим фрикционный контакт длинномерного скользящего элемента (стержня), боковая поверхность которого конвективно сообщается с окружающей средой. Величина теплового потока, направленная от поверхности стержня в окружающую среду qп может быть определена зависимостью q п = а п (Тп — То), (7)

ходить интенсивное изнашивание щеточного ворса за счет абляции ее материала. Абляция будет зависеть от глубины прогрева материала лески.

Критическим случаем трения может быть достижение поверхностью контакта одного из контртел температуры плавления TПЛ. Здесь трение будет иметь гидродинамическую природу и коэффициент трения определим в соответствии с законом Ньютона

v fтр   Ир * е ,

Р ⁵ р

где: 5 _р - толщина расплавленной пленки; ц р

- коэффициент динамической вязкости расплавленного материала при температуре, близкой к температуре плавления. Математическую модель такого процесса можно строить на постановке и решении задачи Стефана [5] с учетом уравнения теплового баланса на границе раздела твердой и жидкой фаз в виде q1 =-XTд%r + r1p1 S, где: 5 - скорость про плавления; р1 - плотность расплава; r1 - скрытая теплота плавления.

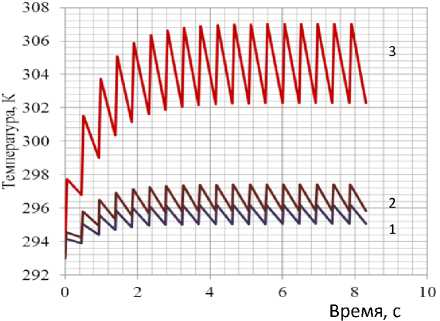
Рисунок 2. Зависимость температуры контактной поверхности Т п от времени ( D = 550 мм , п = 270 об / мин ) при ширинах контакта Н к : 1 - Н к =70 мм; 2 - Н к =100 мм; 2 - Н к =250 мм.

При допущении, что расплавленная часть сразу же переносится на контртело (плавление с абляцией), а фронт плавления движется вглубь скользящего элемента со скоростью 5, текущее значение толщины расплавленной пленки 8 р определим следующим:

8р = 5h4, (10) где h - ширина площадки касания в направле- нии скольжения.

Текущее значение интенсивности изна- шивания L и

Iи = 5ЛС,(11)

где 5 - скорость плавления поверхности трения

[5]:

л = 9 1- ^1/ зср(Т _пл -T₀)S

.      - [г+2/3с(Тпл-70)]р, где 8 - скорость прогрева материала скользящего элемента, с учетом (3.11)

8 = к2к(13)

Далее температура поверхности не пре- вышает температуры плавления, т.е. остается практически постоянной, а температурный профиль после оплавления материала относи- тельно фронта плавления определяется координатой г-5. Толщина прогретого слоя соответствует значению 5-5, где 5 - глубина проплав- ления.

Величина износа в случае проплавления приближенно определиться зависимостью, полученной в работе [5]

)    J^ g(t)dt- ¹ / ₃ cp(r _n, -Т о )Уб5(У?-уё п; )

^(t) =           [г+ ² / ₃ с(Т _пл -7 0 )]p           .

Учитывая то, что в большинстве процессов глубина прогрева материала в процессе трения остается небольшой, а механические свойства при приближении температуры кон- тактной поверхности к температуре плавления интенсивно падают, то достижение факта плав- ления в данном случае вряд ли возможно из-за уноса нагретого материала за счет абразивного изнашивания. Расчеты по формулам (9 – 14) целесообразны только для относительно больших поверхностей контакта и высоких контактных напряжений. Последние условия не могут быть достигнуты, например, в случае трения полипропиленовой щетки.

Введем в рассмотрение коэффициент, учитывающий динамичность процесса трения за счет изменения характеристики пластично- сти материала скользящего элемента

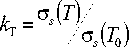
(рис.3), тогда изменение коэффи- циента трения от его начального значения определится формулой fтр = f 0 * kT. В частности для полиамидной лески значение kT аппроксимировано полиномом четвертой степени kT=1,295–0 ,034 Т+0,0012 Т2 – 1,474 10-5

Т ³+5,607 10^-8 Т ⁴. (15)

Если принять во внимание тот факт, что интенсивность абразивного изнашивания связана с разрушением материала, т.е. пропорциональна характеристикам, определяющим его прочность, то можно допустить, что и интенсивность изнашивания также будет возрастать от начального значения /i0 обратно пропорционально коэффициенту разупрочнения:

' 1 = '¹⁰/к_т - (16)

Определение изменения коэффициента трения и интенсивности изнашивания при моделировании процесса является ключевым, поскольку его значение будет определять силовое и тепловое воздействие на ворс щеток и определять его изнашивание.

При анализе процессов контактного взаимодействия твердых тел при высокоскоростном трении в большинстве случаев контртело можно принимать абсолютно жестким (так как 6 1 ^ б₂), а нагретые поверхностные слои скользящего элемента деформируемыми.

Тепловую задачу трения в соответствии с (4 – 14) на современном инженерном уровне можно решить только в случае, если задан теп- ловой поток q1 на границе контакта внутрь рассматриваемого элемента. Поскольку тепловые потоки q1 и q2 проходят вглубь скользящего элемента и контртела, соответственно, вследствие их теплопроводности, то предполагается, что доли интенсивностей тепловыделения, направленные в сторону скользящего элемента и контртела составляют только соответствующие части мощности, высвобождаемой при трении q = атпfpvcP; q2 = (1-атп)fрv=p, (15) т.е. соответствии с известным коэффициентом распределения тепловых потоков а тп.

поверхность контакта скользящего элемента нагревается от теплоты трения и охлаждается набегающими более холодными частями полу-

пространства.

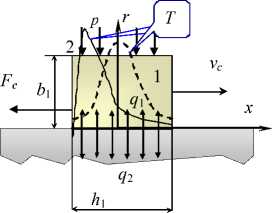
Рисунок 4. Схема фрикционного контакта : 1 – распределение температуры при малых скоростях скольжения; 2 – распределение температуры при больших скоростях скольжения

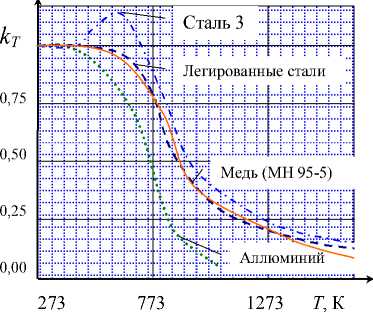
Рисунок 3. Диаграммы разупрочнения материалов от температуры

Известны и другие выражения для атп:

-формула И.В. Крагельского [8], рекомендованная для расчета при больших скоростях скольжения (при Pe>20)

а

тп

4-X ₁           .

4-X , +X ₂ ^п-Pe ₂ ’

-формула А.В. Чичинадзе [7], получен-

ная для случаев кратковременного торможения

а тп

При малых скоростях скольжения значения долей интенсивностей тепловыделения в виде тепловых потоков q 1 и q 2 будут пропорциональны коэффициентам теплопроводности материалов X 1 и X ₂ пары тел, находящихся в контакте. Можем записать в виде, предложенном Х. Блоком [2] а _тп = ^ "^^ . При больших скоростях максимум температуры смещается от центра контакта к грани, противоположной направлению скольжения. При определении коэффициента распределения тепловых потоков в этом случае X. Блок приравнивает наибольшие

. 6 , -X 2 ( 13 т N + FO 1 -т , ) 1 +-

6 2 -X ! ( 1/3 т N + FO 2 -т , )

- 1

, (17)

где соответствующие глубины прогретого слоя

6 1 и 6 2 определяются из соотношения

6 1 , 2 = 1 , 73 - ^1 , 2 - t_T . т n и т , -временные характеристики мощности и работы трения;

-формула А.В. Чичинадзе, В.М. Горюнова [5], полученная для пластически деформируемого скользящего элемента и для Fo < 10

а

тп

1 + ^ 2 -X 1

п - a 1 - v - t_T 3 - a ₂ - d 1

- 1

где d 1 – диаметр пятна касания;

значения температуры: в центре контакта – для неподвижного тела и на задней грани контакта

– для движущегося тела, что является весьма приближенным.

Выражение для а _тпв случае больших скоростей и бесконечно долгого скольжения с постоянной скоростью ( v с =const), получено Д.

Проведем расчет а _тп по приведенным формулам для случая скольжения полипропиленового скользящего элемента толщиной b ₁ =0,25 м и шириной h 1 = 0,003 м по асфальтовой направляющей толщиной b ₂ =0,25 м при постоянных (усредненных) скоростях v 1 =10 м/с, v 2 =50 м/с, v 3 =100 м/с, в течение времени t T =1,0

Егером в виде [2]:а _тп =

1,25Л₁а 1 ^/2

торое

1,75Л1

преобразуется

1,25Л1а.

к

: Ц²+"2^ )^1/2

, ко-

виду:    « тп =

1,25Л1+Л2Ре.

177 . В соответствии с данным выра- ' 2

c

Основные данные расчета:

X i =X₂=0,18 Вт/(мК); а 1 = а ₂=1,? ' 10 " ⁷ м²/с;

6 1 = 6 ₂ = 1,73 - V a (. - t_T = 2,26 - 10 ^{- 4}м;

жением с ростом скорости (числа Пекле) величина атп уменьшается. Физически это объясняется тем, что контртело нагревается как за счет

Foj = Fo₂ = a Ll t T = ₆ , ₈ - 10 ^{- 8}; ^т N =1;

1       2       b ₁         ,

теплоты трения, так и за счет уже нагретых поверхностных слоев скользящего элемента, а

т , =1000; Pe, = v² - t/ .

2          a ₂

Результаты расчета α _тп представлены в таблице 4. Из приведенных в таблице 4 результатов следует, что коэффициент распределения теплоты в скользящий элемент, рассчитанный по формулам Д. Егера мал, причем результаты, полученные по другим формулам значительно отличаются друг от друга. Это различие объясняется тем, что, с одной стороны они рекомендованы для расчета при высокоскоростных режимах трения в основном с нестационарным процессом распространения теплоты вглубь контактирующих тел, с другой стороны не учитывают особенности контактного теплообмена, изменяющегося с течением времени. При этом формулы (17) и (18) дают относительно близкие результаты и получены при режимах движения и условиях, близких к рассматриваемому случаю.

Таблица 4. Зависимость α _тп от скорости

Автор формулы	Средняя скорость скольжения, м/с
	10	50	100
Д.Егер	0,5	0,5	0,5
И.В.Крагельский	2,9 10-4	5,8 10-5	2,9 10-5
А.В.Чичинадзе,	2,3 10-4	4,5 10-5	2,3 10-5
А.В.Чичинадзе, В.М.Горюнов	0,052	0,024	0,017

Истинное значение α тп может быть определено экспериментально путем измерения температур, что представляет определенные трудности в условиях кратковременного процесса высокоскоростного трения. Определение теплового потока q 1 производится путем решения обратной задачи теплопроводности при известной (измеренной в эксперименте) температуре поверхности Т П и на некоторой глубине T ( t,r ).

Значения α тп найденные при этом могут также значительно отличаться от действительных, отражающих текущий процесс и характеризуют лишь среднюю величину теплового потока за некоторый промежуток времени взаимодействия.

С учетом сказанного, для кратковременных процессов, предпочтительно использовать аналитические выражения для α тп , уточняя их путем согласования по экспериментальным данным конечных значений характеристик процесса, например – температуры поверхности.

В работе [7] проведен анализ модели трения и изнашивания для случая трения полиамидной лески по поверхности абразивного круга. В результате сравнения расчетных данных с опытными (рис.5) установлена адекватность имитационной модели в случае примене- ния для расчета αтп формулы А.В. Чичинадзе, В.М. Горюнова (18) Средняя ошибка аппроксимации при этом не превысила значения 12%. В то время как применение для расчета αтп формулы Д. Егера приводит к заниженным значениям αтп , следовательно – к заниженным температурам и износам.

Выводы

• 1.    Разработана имитационная модель высокоскоростного трения и. Модель основана на расчете нагревания зоны контакта скользящего элемента и отводе тепла в окружающую среду.

• 2.    На основании исследования температурных полей обоснована возможность применения для процесса нагревания и отвода тепла уравнений, определяющих стационарный режим с граничными условиями третьего рода.

• 3.    Предложено рассчитывать износ скользящего элемента путем определения интенсивности абразивного изнашивания в зависимости от механических (абразивных) свойств материала лески щеточного ворса и характеристик высокоскоростного силового взаимодействия ворса с очищаемой поверхностью. Изменение интенсивности износа в процессе трения определено через изменение механических свойств материала лески от температуры.