Имитационное моделирование распространения загрязнений в реках

Поведение примеси в водной среде зависит от многих факторов: химических (распад, соединение с другими веществами, выпадение в осадок); физических (переход в другое агрегатное состояние, адсорбция, коагуляция); гидродинамических (перенос те и рассеяние в процессе турбулентной диффузии); биологических (аккумуляция и перенос морскими организмами). Задачи распространения вещества в стационарном водном потоке в общем случае описываются системой дифференциальных уравнений в частных производных, включая в себя уравнения Навье - Стокса и уравнение переноса вещества, учитывающем физикохимическое взаимодействие примеси со средой и наличие источников примеси [ 1 ].

Пусть неконсервативная примесь распространяется в двумерном нестационарном потоке через горизонтальный непрямолинейный канал, длина которого много больше его ширины (рис. 1).

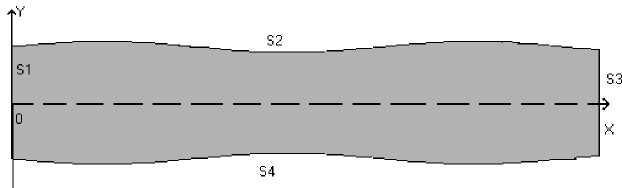
Рис. 1 Схематическое изображение русла реки

Рассмотрим систему уравнений, описывающую процесс переноса вещества в двумерном стационарном потоке вязкой несжимаемой жидко- сти [ 6 ]:

ди    ди    ди 1 дp ( д2 и      д2 и --+ и--+ v— = ---— + и + Ц., + F д t    дx    ду р дx x V дx2     у ду2 у д v    д v   д v 1 дp ' 22 д v     д v --+ и--+ v— = ---— + ^ + ^, + F д t    дx    ду Р ду x V дx2    у ду2 J д и д v _ — + — = 0 дx ду

u 1 5 2, 5 4 = v 1 5 2, 5 4 = 0, P 1 5 1 - P 1 5 3 = ^П

d c   d c   5 c

--+ u --+ v— d t     d x    d y

D x

d2 c      d2 c p 2 + Dy p 2

о x      d y J

- X c + f

d c               d c

^ 1 5 2 , 5 4 = ⁰         7^1 5 , = a ( У, t )         ^c ( О, У ) = ⁰

Уравнения (1), (2) описывают гидродинамическую часть задачи, в которой неизвестными функциями являются продольная и поперечная составляющие вектора скорости u=u(x,y), v=v(x,y) и давление p=p(x,y). Плотность жидкости р и коэффициенты вязкости рх и py считаются постоянными, предполагается также отсутствие внешних источников сил F=0. На бе- регах потока задаются условия прилипания, а на границах входа и выхода потока разность давления.

Уравнения (3), (4) отвечают «концентрационной» части задачи. Неизвестной функцией является c=c(t,x,y) - распределение концентрации вещества. Коэффициенты диффузии D_x и D_y (теплопроводности в случае распространения температуры), параметр распада X , функция источника / считаются постоянными. Функция a(y,t) определяет распределение вещества через входное сечение канала. Обычно она имеет следующий вид: a ( у , t ) = A ( y ) [ H ( t ) - H ( t - 1 ₀ )] , где H(t) - функция Хевисайда, что отражает временной характер некоторого выброса и его конечность.

Для неканонических областей, какими и являются естественные во- доемы, задача распространения вещества не поддается исследованию аналитическими методами. Среди прямых численных методов расчета задачи (1) - (4) наибольшую популярность завоевали методы конечных разностей [14] и методы конечных элементов [13], [14],[15],[16],[17].

Параметры гидродинамической подсистемы (плотности жидкости, ее вязкость) должны зависеть от концентрации примеси. Однако в большинстве случаев, с целью упрощения модели, этой зависимостью пренебрегают, т.е. примесь считается пассивной. В моделях, где концентрация примеси относительно мала (в большинстве задач водной экологии оказывается именно так), такое упрощение вполне оправдано [7], [2]. При таком предположении гидродинамическую подсистему (1, 2) можно решать независимо от уравнения для концентрации (3, 4).

Решение подобных задач разделяется на два этапа: на первом шаге должно быть рассчитано поле скорости и поле давления, на втором - распределение концентраций примесей при найденном на первом шаге поле скорости.

Наиболее распространенным подходом к решению второй задачи является рассмотрение ее как стохастического процесса. Для этого собирается эмпирический материал о функционировании системы и на его базе строится прогноз на будущее. Однако среднестатистический характер такого прогноза не позволяет судить о процессах в локальных зонах. К тому же он не дает ответа на вопрос о воздействии на экологическую систему форс-мажорной техногенной нагрузки (например, выброс грязных, химически активных вод с судна, стоящего в затоне, осадки).

Одним из достаточно полных методов анализа факторов, влияющих на состояние экологической системы, является их имитационное модели- рование с помощью универсальных программных комплексов. Причем полноценная обработка и осмысление результатов моделирования гидро- динамических явлений в потоке невозможны без многофункциональной системы постпроцессинга, позволяющей визуализировать результаты в ви- де векторной структуры потока, изолиний в секущих плоскостях или изо- поверхностей в пространстве и т.п.

Приведение к конечно разностной системе уравнений

На основе метода конечных разностей (рис. 2) и учитывая особен- ность канала с учетом системы уравнений (1) описывающие гидродинами- ческую составляющую задачи, краевые условия (2) и уравнения отвечаю- щие за концентрацию вещества (3, 4) построена конечно-разностная сис- тема уравнений в общем виде:

u k

—

uh

h

+

uv i + 0.5, j + 0.5

—

uv i + 0.5, j — 0.5

h

+ !( p ' '

—

Pk)

P

h

■)^— A x

^ui + 1.5, j

—

² u i + 0.5, j

h h

⁺ u i — 0.5, j

—

A y

u i + 0.5, j — 1

—

² u i + 0.5, j

h2

⁺ u i + 0.5, j + 1

—

⁽ u i

, n + ¹

' i + 0.5, j

—

^uiⁿ + 0.5, j ⁾

d t

u i + 1, j

—

uh

h

+

uv i + 0.5, j + 0.5

—

uv i + 0.5, j — 0.5

h

+ !( p + j

—

^pi , j

P

h

) ^— A x

^ui + 1.5 j

—

² u i + 0.5, j

⁺ u i — 0.5, j

h h

—

A y

u i + 0.5, j — 1

—

² u i + 0.5, j

⁺ u i + 0.5, j + 1

h ²

—

( u_i

, n + ¹

i + 0.5, j

—

d t

u + J (5)

u i — 1,J

-

ui + 1,J

d x

+

v i , J — 1

-

vi, J + 1

d y

= 0

^U I S 2, S 4

= v ¹ S 2, S 4

= ⁰ P | S ,

- P | S 3 = ^П

k + 0.5

C -i , j

-

k

C -i, J

t

+ u

k

i + 1, j

D x

k ci+1, J

-

V

k ci+1, j

-

k c

• i ^{—    1}, J

+ u

k

k ci+1, j

-

k

c i—1, J

x

i — 1, j

+

k

x

^vi , j + 1

k

c i , j —1

-

y

k

C -i , J

+ v

k

i , j + 1

k

c i ,j —1

-

y

k

C -i , J

2 c ^k . + c i , ^J

2 x

S c _ d n ^{S 2} , ^{S 4} =

k

i — 1, j

+ D

y

k

• i ,    J — 2

-

2 c

k

i , j — 1

+ c

k

i , j

2 ^y

—

A c

dc  _ dn S1 =

a ( У, t )

c ( 0, y ) = 0

d x — шаг по оси х ; d y

—

шагпооси у .

В дальнейшем будем рассматривать неразрывные во времени про- цессы t/ = 0 и несжимаемую жидкость, для которой справедливо урав-

Рис. 3. Алгоритм.