Имитационное моделирование режимов работы солнечных установок с фотоэлектрическими преобразователями в зависимости от внутренних и внешних факторов в среде MATLAB/Simulink

Одним из способов повышения эффективности СУ с ФЭП является использование системы слежения за Солнцем, которая позволяет увеличить выходную мощность ФЭП и дневной интервал генерирования электрической энергии. Одновременно это ведет к усложнению конструкции, снижению надежности и удорожанию СУ в целом. Поэтому целесообразность применения систем слежения в СУ с ФЭП определяется после проведения соответствующих расчетов и исследований с учетом внешних (приход солнечной радиации на поверхность ФЭП, температура окружающего воздуха на месте предполагаемой эксплуатации установки) и внутренних (определяются свойствами исходного полупроводника, технологией изготовления фотопреобразователя и параметрами ФЭП) факторов.

Исходя из этого сформулирована цель работы: исследование работы СУ с учетом влияния внешних и внутренних факторов и степени ориентации приемной поверхности ФЭП на Солнце.

Для достижения сформулированной цели в настоящей работе поставлена задача: разработать математическую модель для определения энергетических показателей СУ с ФЭП в зависимости от внутренних и внешних факторов и степени ориентации приемной поверхности ФЭП на Солнце.

Методика и результаты исследования. В основу математического моделирования была заложена классическая модель фотопреобразователя с p-n переходом [1]

A • k • T U =--In

q

(Jф - J) + 1

J o

- JR,

где U – напряжение, В; k – постоянная Больцмана, Дж/К; T – рабочая температура ФЭП, К; q – заряд электрона, Кл; JФ – фототок, пропорциональный интенсивности солнечного излучения I , падающего на поверхность ФЭП

(J          A

— = const

11        J

, А/см ² ; J - ток, А/см ² ; J o - обратный ток насыщения, определяемый

свойствами исходного полупроводника и технологией изготовления ФЭП, определялся из выражения (1) при условии J = 0 и U = UХХ, А/см2; R - внутреннее электрическое сопротивление, Ом^см2; A - без размерный параметр кривизны вольт-амперной характеристики (ВАХ), A = 1...2 [1].

Для исследования энергетических характеристик СУ с ФЭП была разработана математическая модель, реализованная в программной среде Matlab/Simulink (рис. 1).

Математическая модель позволяет оценить влияние на выходные характеристики модуля ФЭП как внутренних (число последовательно, параллельно соединенных элементов, внутреннего сопротивления), так и внешних факторов (интенсивности солнечного излучения, температуры воздуха, степени ориентации модуля ФЭП на Солнце в зависимости от времени года и суток).

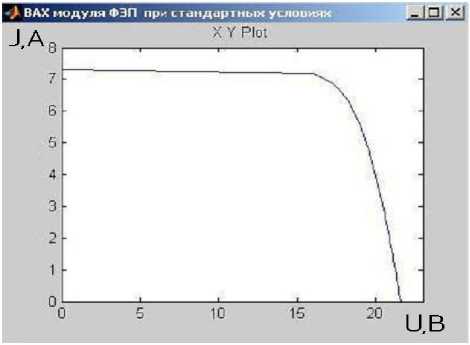
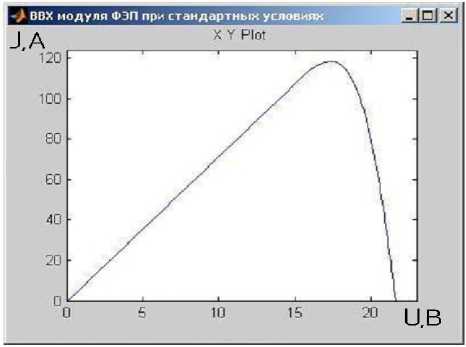
В целях ее апробации построены ВАХ и вольт-ваттная характеристика (ВВХ) для модуля ФЭП, состоящего из 2 параллельно соединенных блоков (с 36 последовательно соединенными элементами в каждом), при стандартных условиях освещения АМ1 ( 1 ₀ = 1000 Вт / м ² ) и рабочей температуре T₀ = 25 ° C (рис. 2).

Фотоэлементы из монокристаллического кремния имеют следующие характеристики: Jo _{К . З .} = 47 мА/см²; u o _ХХ = 600 мВ; R =1 Ом·см²; площадь S=98,92 см²; значения коэффициента приняли A =1,2.

Фотоэлектрический модуль, согласно паспортным данным, выдает максимальную мощность P _max

=120 Вт, U_ХХ =22 В, J _{К . З .} =7,34 А, оптимальное рабочее напряжение U_ОПТ =18 В и ток J _ОПТ =6,66 А.

Рис. 1. Математическая модель СУ с ФЭП в программной среде Matlab/Simulink

Как видно из рисунка 2, полученные характеристики совпадают с паспортными, что подтверждает адекватность разработанной модели.

Однако реальные характеристики ФЭП значительно отличаются от стандартных вследствие изменения параметров внешней среды (интенсивности солнечного излучения и температуры воздуха), которые зависят от географического положения предполагаемой эксплуатации установки, времени года, суток и степени ориентации Су на Солнце.

а

б

Рис. 2. Характеристики модуля ФЭП при стандартных условиях освещения АМ1 и рабочей температуре

T 0 = 25 ° С : а - ВАХ; б - ВВХ

Влияние изменения интенсивности солнечного излучения и рабочей температуры на ВАХ ФЭП можно записать в виде выражений [2]:

J К . З . = Jo К . З . + ^{A J}I + ^{A J} T ;

UY =U UoYy+UU„ +A U ++U UT,

ХХ ХХ       11       12

где Jo _K . З . и Uo ХХ - исходный ток короткого замыкания и напряжение холостого хода, измеренные при стандартных условиях; A J I , A U 11 , A U ₁₂ - поправки, учитывающие изменение плотности потока солнечного излучения; A J т , A U_т - поправки, учитывающие изменение рабочей температуры:

• aji = J   Jok . з .;

A UIi = -AJi • Rn;(5)

A Ui 2 = K- 1g 1 ;(6)

AJT = Pi ' JoK.З. (T — T0 ) ;(7)

AUt = в - Uж (T - To) ,(8)

где R _n - последовательное сопротивление элемента; K - коэффициент, зависящий от типа солнечного элемента; в , Р и - температурные коэффициенты тока и напряжения, 1/°С.

В ходе моделирования для определения интенсивности солнечной радиации (прямой, рассеянной и суммарной) на горизонтальную поверхность использовались данные многолетних наблюдений [3]. Для ис- ключения интервалов, интенсивности в которых не известны, использовался метод полиноминальной аппроксимации [7].

Суммарная интенсивность солнечного излучения на стационарную наклонную поверхность, ориентированную на юг, была рассчитана по выражению [1]

_{T т} cos £ _т (1 + cos в )          т Л - cos в

Ih = In ---- + In  ------   + P(In + 1n) ------—,              (9)

H П cos0 Д 2       >’'              2    , где IП , IД – интенсивность прямого и рассеянного (диффузного) солнечного излучения на горизонтальную поверхность, Вт/м2; 0 - угол между направлениями на Солнце и зенит, в град, определяется по формуле (10); £ - угол между направлением на Солнце и нормалью к наклонной поверхности, ориентированной на юг, в град, определяется по формуле (11); в - угол наклона рассматриваемой поверхности к горизонту, в град; р - коэффициент отражения (альбедо) поверхности Земли и окружающих тел [3].

cos 0 = sin ^sin ^ + cos J cos фcos a.(10)

cos £ = sin(ф - в) sin J + cos(ф - в) cos J cos a,(11)

где J - склонение Солнца, определяется по формуле Купера, в град [1]; ф - широта местности, в град; a - часовой угол движения Солнца, в град.

Часовой угол рассчитывался по формуле [5]

a = (15°часД^,. -12), где tsolar – локальное солнечное время, в часах.

Расчет суммарной интенсивности солнечного излучения на приемник, расположенный под углом в и ориентирующийся на Солнце только по одной координате (азимутальное слежение), производился по формуле (9), с разницей в нахождении угла между направлением на Солнце и нормалью (вместо £ используется i ). Данный угол определялся по формуле [6]

cos i = sin в [cos J (sin ^ cosa П cos a + sin a П sin a ) -

• - sin J cos ^ cosa П ] + cos в [ cos J cos ^ cos a + sin J sin ф ]

где a _П – азимут приемника.

При слежении за Солнцем по азимуту азимут приемника равен азимуту Солнца ( а _п = a ) и определялся по формуле [6]

a = arcsin

^ cos J sin ф

V cos a J

,

где a - угол высоты Солнца, определялся по формуле

α= arcsin(sinδsinϕ+ cosδcosϕcosω) ⇒α= arcsin(cosθ).

Суммарная интенсивность солнечного излучения при полной ориентации поверхности была рассчитана по выражению

I (1+cosθ)             1 - cosθ

IОР = П +IД            +ρ(IП +IД)         .           (16)

cosθ        2                   2

Для расчета температуры окружающего воздуха были привлечены ежечасные данные по температуре окружающего воздуха, приведенные в справочнике [4], и применялась аналитическая зависимость изменения температуры воздуха в течение времени, учитывающая среднесуточную, суточную амплитуду, период изменения температуры воздуха [7].

Все вышеприведенные выражения были учтены в разработанной математической модели.

Результаты моделирования работы модуля ФЭП, характеристики которого приведены выше с учетом в I =0,0006 °с - ; в и =-0,0032 с , для климатических условий п. Кушнаренково Республики Башкортостан (РБ) ( ϕ = 54°) в 17ч локального солнечного времени 22 июня представлены на рисунке 3.

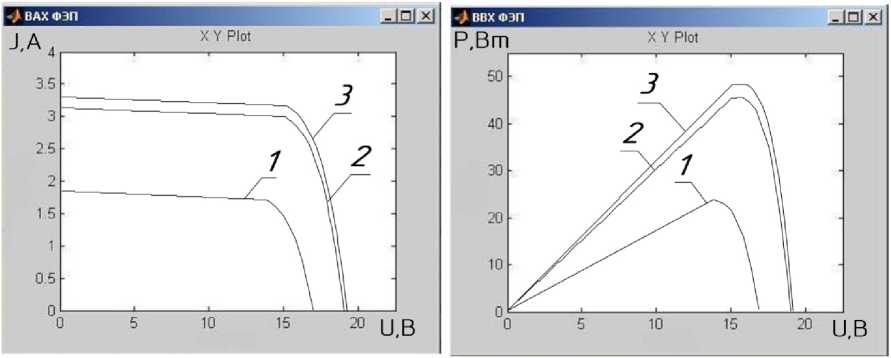
Анализ показывает, что пиковая выходная мощность модуля ФЭП с системой слежения за Солнцем в указанное время в два раза больше мощности стационарного. Причем полная ориентация модуля на Солнце дает практически те же характеристики, что и при частичной (азимутальной) ориентации.

а                                           б

Рис. 3. ВАХ (а) и ВВХ (б) модуля ФЭП, установленного в поселке Кушнаренково РБ для 22 июня 17 ч локального солнечного времени: стационарного (1), с азимутальным слежением (2) и расположенного под углом к горизонту в = 35°; с полной ориентацией (3)

На рисунке 4 представлены дневные выработки мощности СУ при различной ориентации ФЭП в тех же климатических условиях в середине лета, осени, зимы и весны.

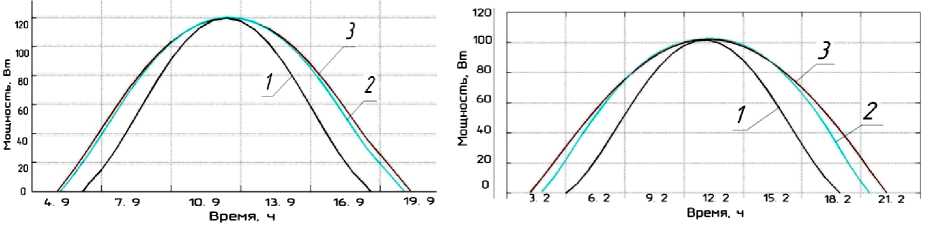
Вырабатываемая в течение светового дня 15 апреля мощность ФЭП с азимутальным слежением на 28 % больше мощности, вырабатываемой стационарной системой (рис. 4, а). Система с полной ориентацией на Солнце эффективнее азимутальной на 3,5 %. Соответственно для 15 июля (рис. 4, б) мощность ФЭП с азимутальным слежением на 34 % больше стационарной системы. Полная ориентация ФЭП увеличивает выходную мощность на 55 % по сравнению со стационарной системой и на 16 % по сравнению с азимутальным слежением. Для 15 октября (рис. 4, в) применение азимутального слежения увеличивает выходную мощность на 5 %, а полное слежение – на 8,5 % по сравнению со стационарной системой. 15 января (рис. 4, г) соответственно на 5 и 17 %.

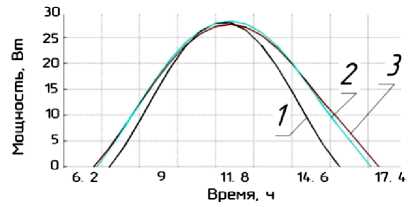
б

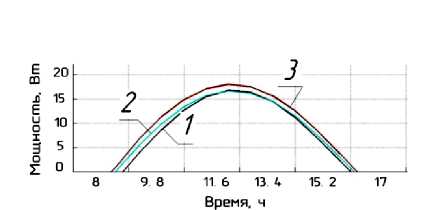
в                                                                    г

1 при неподвижном ФЭП, расположенном под оптимальным углом β к горизонту

• 2    при азимутальной ориентации ФЭП, расположенного под оптимальным углом β

• 3    при полной ориентации ФЭП на Солнце

Рис. 4. Графики зависимости вырабатываемой мощности ФЭП, установленного в поселке Кушнаренково РБ: a – для 15 апреля; б – для 15 июля; в – 15 октября; г – 15 января локального солнечного времени

Выводы. Разработана математическая модель для определения энергетических показателей СУ с ФЭП в зависимости от внутренних и внешних факторов и степени ориентации приемной поверхности ФЭП на Солнце. Сравнение характеристик, полученных при моделировании в стандартных условиях, с паспортными характеристиками подтверждает адекватность разработанной модели. Моделирование режимов работы для произвольно выбранных дней времен года на основе данных многолетних климатических наблюдений в условиях п. Кушнаренково РБ показывает эффективность применения систем слежения за Солнцем.

Анализ энергетических показателей СУ с ФЭП с различной ориентацией на Солнце за необходимый период времени позволит дать оценку о целесообразности применения систем слежения в данных установках.