Имитационное моделирование сложных технических систем авиационной техники с использованием сетевых методов

Таким образом, объект [5] ПО G ^a е S будем описывать следующей совокупностью множеств:

S = { G , B , О , О , Y , Z , H , V , U }.      (1)

где S - система;

G a - множество образующих, представляющих собой конкретную подсистему 0 ;

B - структура связей;

Т – множество моментов времени;

X – множество входных сигналов;

Y – множество выходных сигналов;

Z – множество состояний;

H – множество внутренних параметров;

V – множество случайных операторов;

U – множество характеров состояний системы.

Формальная модель (1) позволяет организовать моделирование процессов функционирования системы АБСУ или одну из ее составных подсистем с учетом возникновения отказов и неисправностей компонентов системы методом итерационного процесса вычислений [4]. Состояние системы z₂ ( t _i+1) в некоторый момент времени t _i+1 после наступления i- го отказа определяется ее текущим z₁ ( t_i ) состоянием и вероятностью появления i- го отказа. Можно считать, что процесс смены состояния в данном случае является следствием произошедшего повреждения одного из компонентов системы АБСУ или нарушением одной из функциональных связей.

Методическая сложность учета влияния отказов элементов возникает при сложной структуре взаимосвязи и взаимодействия компонентов объекта ПО. Наиболее сложными случаями моделирования процессов функционирования является моделирование разветвляющихся процессов, а также схем с резервированием [4].

Для схемы с последовательным соединением элементов выход из строя одного из них приводит к нарушениям выходных характеристик всей системы. Поэтому в целях упрощения участки схемы с последовательным соединением элемен- тов будем представлять в виде одного обобщенного элемента - макропозиции Q.

Временная последовательность отказов элементов легко учитывается в макро-E-cетевых моделях процессов функционирования, так как в них динамика смены состояния может быть непосредственно увязана со временем.

Формально макро- E -сеть определим множеством MEN [6]

MEN = ( D, О, B , R ) ,           (2)

где: Р – конечное множество позиций;

Т – конечное непустое множество переходов;

B - множество связей образующих, соединяющих между собой множество позиций и переходов;

R - множество функциональных правил (ограничений).

D = ( g , r , Q ),                 (3)

где g – образующие – простые позиции;

r – решающие позиции, минимальная совокупность которых определяет выбор контролируемых точек оценки состояния объекта ПО;

Q – макропозиции модели.

Множество переходов

О - { О^О , О⁴ , O N , O F , T J , T^c g , T X , T Y }     (4)

описывает базовые структуры переходов, которые подразделяются на простые переходы Т^T , переходы “исполнение” – Т^Е , “включение” – Т^N , “выключение” – T^F , “разветвление” - T^J , “перераспределение” – T^(cg) и макропереходы Т^X – (“распределение”) и Т^Y – (“выбор”).

Дуги P e G связывают вершины Р и Т по следующему правилу [2]: начало и конец любой дуги соединяет только разноименные вершины Р и Т, т. е.

D п ‘Л = Q.              (5)

Функциональные правила включают в себя

R = ( m , b , R, L ),                 (6)

где:

m : P    ( 0 , 1 ) – разметочная функция, (7)

b: T L – функция обозначения, (8) R – решающая функция,

L= U п V- используемый алфавит, (9) где: U – входной алфавит сигналов управления,

V – выходной алфавит сигналов управления.

Разметочная функция т устанавливает в каждой позиции p_e в соответствии с правилом срабатывания переходов определенное число меток S=(0,1).

Функция обозначения b показывает, какие входные сигналы U из внешней среды влияют на срабатывание переходов T и какие воздействия формируются в сети в результате их срабатывания.

Решающая функция R позволяет указать позиции, от которых зависит срабатывание перехода T в рассматриваемый момент времени, и указать позиции, в которые должна перейти метка после его срабатывания.

В макро- E -сетях решающие позиции r_s позволяют реализовать управление появлением меток в одной или нескольких простых позициях р_e с помощью внутренних связей.

Пример сетевой модели продольного канала АБСУ-154-2 в режиме автоматического управления с использованием макро- E -сетевых моделей, построенной с учетом возможных повреждений компонентов системы приведен на рис. 1.

Функциональная диагностическая модель — базовая структура для построения графической модели и матрицы состояний продольного канала АБСУ. На основе теории графов построим графическую диагностическая модель продольного канала АБСУ в режиме стабилизации высоты и управления.

Состояние представленной модели может быть охарактеризовано с помощью ориентированного графа, в котором число узлов равно числу конечных состояний системы, а число ребер всей совокупности возможных переходов из одного состояния в другое.

Графическая диагностическая модель продольного канала АБСУ, представленная на рис. 2 характеризуется множеством входов P ( p₁...p_п ), множеством выходов U ( u ₁ ...и_т ), множеством вершин T ( t ₁… t _S) и множеством дуг G ={( P _l P 2 ),( в . в з ),( P 2 P 4 >-}-

Теория графов допускает возможность формальных преобразований одного графа в другой, упрощения многочисленных связей, что позволяет в отдельных случаях минимизировать число вершин, отражающих структуру графа, а, следовательно, число блоков, подлежащих контролю.

Одной из модификаций информационной модели может быть матрица ее состояний. Матрица состояний – формализованный документ. Матрица состояний диагностической модели дает полное описание множеств состояний S ( s₁...s_n ) , множеств проверок или сигналов U ( u ₁ ...u_k ). Число состояний п = 2к, где k – число выходных сигналов, равное числу функциональных блоков. Общее число проверок в схеме 2^k -1. В матрице состояний каждый столбец (строка) проверок характеризуется определенным количеством информации о работоспособности всей системы или отдельной группы блоков. Количество информации о работоспособности соответствует числу единиц, а количество информации о неработоспособности – числу нулей. Проведя все положенные проверки, можно определить не только отказ, но и отказавший блок модели и функциональной схемы.

АБСУ как объект технического диагностирования может находиться в п состояниях поля

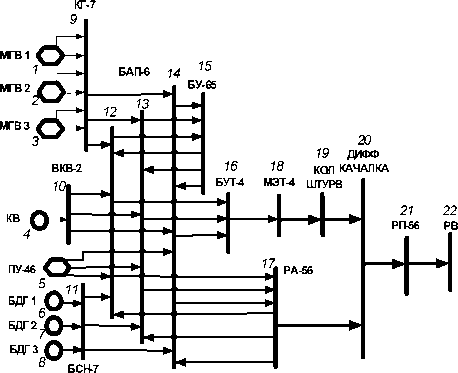
Рис.1. Сетевая модель продольного канала АБСУ в режиме автоматического управления

5 , причем s i с ! S , i=1,.. i ". В качестве состояний системы АБСУ могут рассматриваться работоспособное или неработоспособное состояния отдельных блоков, входящих в систему, или отдельные значения параметров (параметр в допуске, не в допуске или принадлежит различному уровню квантования). Носителем сообщения является результат проверки п . с ! 1. Минимальное число параметров для контроля работоспособности – внешне устойчивое множество, выбирается путем преобразования функциональной диагностической модели по определенным правилам [7].

Для оценки состояния всего продольного канала системы АБСУ-154-2, сложной системы работающей в режиме автоматического управления, достаточно измерение параметров для кон-

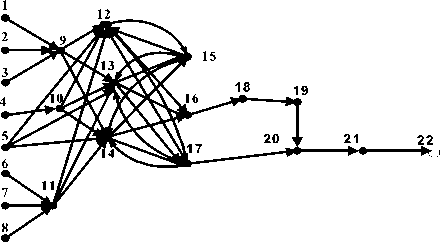
Рис. 2. Ориентированный граф ФДМ продольного канала АБСУ троля работоспособности системы производить по состоянию сигналов на выходах узлов позиций 12, 13, 14, т.е. контроль продольного канала АБСУ следует производить по параметрам решающих позиций - блоков БАП-6 системы АБСУ-154-2.