Имитационное моделирование состояния и функционирования технических устройств и систем

Создание высокоэффективных инженерных систем и оборудования различного назначения предполагает необходимость использования математических методов для моделирования происходящих при их функционировании процессов. Как правило, к реальному объекту – к оборудованию или системе эти математические методы непосредственно не применимы. Для их применения необходимо построить математическую модель функционирования данного объекта. Математическое моделирование предназначено для исследования на базе построенной математической модели свойств моделируемого объекта и происходящих в нем процессов, а также переноса полученных сведений на реальный объект.

Аргументами математических моделей является время и/или координаты пространства. Построению математической модели предшествует физическое моделирование, на этапе которого изучаются физические закономерности происходящих процессов, выявляются значимые и второстепенные факторы и связи. Общая модель должна отражать следующие основные факторы: работоспособность (взаимодействие с внешней средой и другими элементами); энергетический баланс; надежность (запасы прочности, долговечность и др.); экономическую эффективность (стоимость производства и эксплуатации, технологичность и др.).

При создании сложных технических устройств, выделяют две основные группы процедур: анализ и синтез. Для синтеза характерно использование структурных моделей, позволяющих сформировать оптимальный облик устройства путем поиска ограниченного числа параметров с использованием специальных целевых функций. Как правило математические модели синтеза применяются на первоначальных этапах проектирования. Задачи анализа связаны с построением функциональных моделей, оперирование которыми позволяет получить необходимые сведения о техническом устройстве и его функционировании. Математические модели процессов, применяемые для анализа, как правило, более сложные, чем для синтеза по структуре и включают большее число параметров.

Методы моделирования, решающие задачу идентификации математической модели, можно классифицировать четырьмя основными группами: аналитические, численные, имитационные, вероятностно-статистические .

При аналитическом моделировании получают исследуемые характеристики как некоторые функции от входных параметров. Полученное при этом решение наиболее точное, поскольку связывает объекты системы с помощью некоторых функциональных соотношений, сформулированных на основании строгих математических законов.

Интерес к математическому моделированию возрос в значительной степени с появлением ЭВМ, поскольку появилась возможность исследования математических моделей практически любой сложности. Здесь математическую модель функционирования объекта представляют в виде программы для ЭВМ – компьютерной модели, позволяющей проводить с ней вычислительный эксперимент . При исследовании математических моделей на ЭВМ, как правило, используются методы вычислительной математики, основанные на численном (приближенном) решении некоторых уравнений, т.е. – численное моделирование [1 – 3].

Для каждой математической модели может существовать, как правило, несколько методов ее исследования. Например, задачи оценки теплового или напряженно-деформированного состояния элементов изделий во всех случаях представляются дифференциальными уравнениями в частных производных, в совокупности с некоторыми краевыми условиями образующими математическую модель поведения данного изделия. Исследование такой модели заключается в решении системы дифференциальных уравнений при заданных граничных условиях [4 – 5]. Их решение можно произвести с помощью обобщенно- го метода начальных параметров, методом Ритца, методом сеток, методом коллокаций, методом конечных элементов (рис. 1) и т.д.

Задачи динамики движения в большинстве случаев представляются системами обычных дифференциальных уравнений. Решение их производят методами Эйлера, Рунге-Кутта и др. [6].

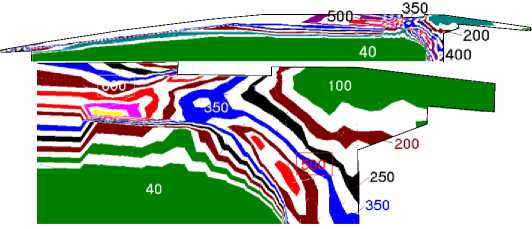
Рисунок 1 – Интенсивности напряжений, МПа (по Мизесу), расcчитанные методом конечных элементов [5]²

Возможности моделирования на ЭВМ неуклонно растут и требуют все больших вычислительных мощностей. Для получения навыков работы с современными компьютерными и программными средствами численного, в том числе имитационного моделирования физических процессов, происходящих при функционировании сложных технических систем применяют различные пакеты программ, обладающие различными возможностями реализовывать решения практических задач в области проектирования и обслуживания машин и оборудования различного назначения. Так для анализа аналитических моделей, как правило применяют наиболее простые табличные процессоры. Более сложные системы уравнений, включающие дифференциальные уравнения, программируются на алгоритмических языках, на базе которых созданы объектно-ориентированные среды Microsoft - VisualBasic, ObjectPascal, Delphi, Co — Array Fortran, Matlab и др.

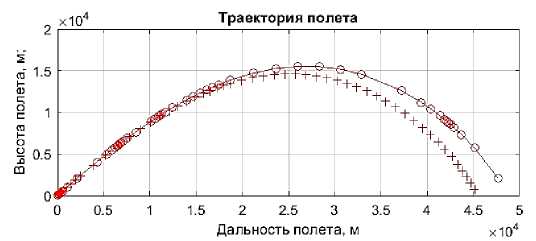
На рисунке 2 показан результат решения прямой задачи внешней баллистики в Matlab. Здесь рассматривается поступательное движение снаряда под действием силы тяжести G и аэродинамической силы сопротивления воздуха R_A 3 , а также реактивной силы P в случаях, когда снаряд имеет реактивный двигатель .

• ²    Иллюстрация авторская из интерфейса пакета программ INNER

• ³    Отметим, что при движении тела относительно Земли со скоростью г, оно, кроме ускорения силы тяжести д, испытывает ускорение Кориолиса i_c , которое определяется формулой Т_с = 2[Л2 х г].

  *| MENU

  
  

  Исходные данные

  
  

  Д Figure 1

  File Edit View Insert Tools Desktop Window Help

  
  

  □ a d -^ | fe | Ч 4^ ® ^ ^ -|a| □ IB| □ и

  
  

  Начальная скорость v0= 900

  
  

  Угол бросания= 45

  
  

  Моделирование движения артиллерийского снаряда в воздухе

  Закон сопротивления 43-года (Уточненая функция Сиаччи)

  
  

  Время полета tk= 120

  
  

  Масса снаряда= 47

  
  

  Значения параметров по умолчанию:

  Масса снаряда, кг-47 Коэффициент формы -1.1 Калибр, мм - 0.152

  
  

  Коэффициент формы 143=1.1

  
  

  Калибр d= 0.152

  
  

  Начальные условия по умолчанию

  Начальная скорость, м/с- 900 Угол бросания, град -45

  Время полета, с - 120

  масса топлива, кг - 3.5

  Время работы РДТТ, с- 10

  Импульс РДТТ, с - 550

  
  

  Продолжить

  
  

Программа airpoint2.m

Закончить работу

| 4000

| 2000

0^

Импульс двигателя 11= 550

ПУСК

а)

-2000L 0

1                      1.5

Дальность полета, м

0.5

1     1.5     2     2.5     3     3.5

Дальность полета, м

4     4.5     5

х1О4

Траектория полета

1.5

2.5 х 104 б)

-10

-20

-30

Угол наклона траектории

х 104 25

1                   1.5

Дальность попета, м

в)

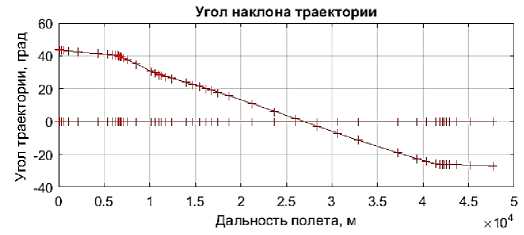
Рисунок 2 - Результаты анализа в Matlab поступательного движения снаряда в атмосфере : а) - управляющая часть программного интерфейса; б) – траектория нереактивного снаряда; в) – траектория активнореактивного снаряда; +— с использованием процедуры ode45 и о — с использованием процедуры ode113

Особенностью Matlab является возможность использования большого количества стандартных процедур для решения типовых математических задач. Здесь для сравнения сходимости результатов решения используются две наиболее часто употребляемые функции ode45 и ode113, реализующие вычисления по методам Рунге-Кутта 4 ÷ 5 по- рядка и Адамса, соответственно. В функции ode23 также реализован метод Рунге-Кутта, но 2÷3 порядка, что может давать меньшую сходимость результатов.

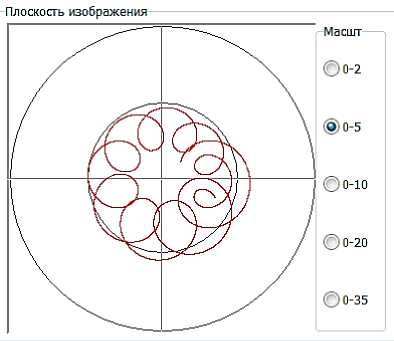
Полная система уравнений движения нереактивного снаряда, как твердого тела в воздухе содержит шесть дифференциальных уравнений второго порядка – три поступа- тельного движения и три вращательного, что создает определенные трудности при исследовании ее в Matlab. Для этой цели была написана программа в объектно-ориентиро ванной среде Delphi (рис.3)

а)

б)

в)

г)

д)

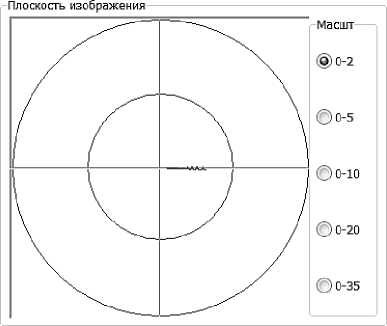
е)

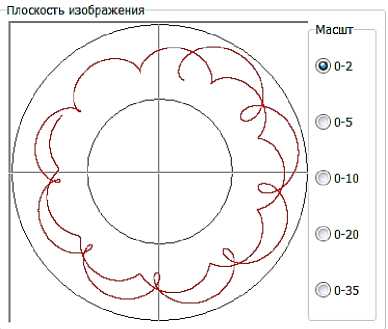
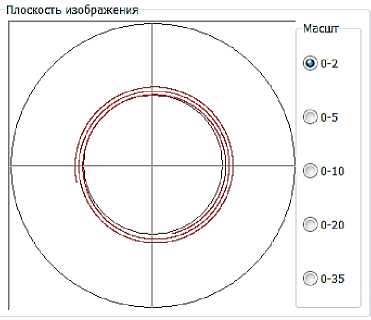
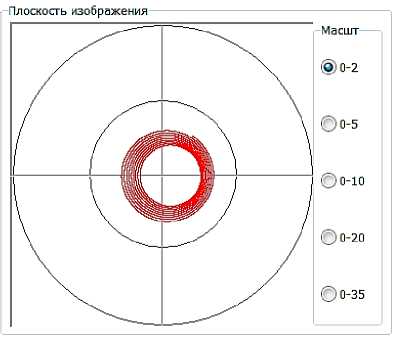
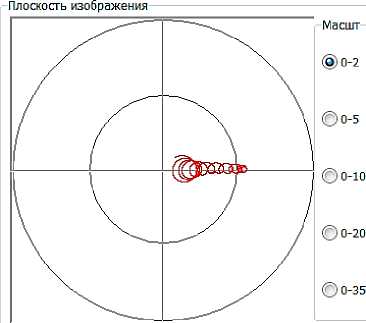
Рисунок 3 – Расчетные эпициклоиды вращательного движения снаряда на траектории⁴ : а) – начало полета; б-через 0,7 с полета; в – на восходящей ветви траектории (2,5 с полета); г – на восходящей ветви траектории (10,0 с. полета); д – в вершине траектории (50 с полета); е – на нисходящей ветви траектории (время полета 77,7с).

• ⁴ Изображения с интерфейса авторской программы, написанной в Delphi

По мере развития компьютерной техники и широкого применения ее в той или иной области произошло накопление программного обеспечения и интеграция наиболее полезного программного обеспечения в комплексные (интегрированные) системы, позволяющие решать широкий круг задач в определенной области деятельности. Так в области инженерной деятельности сформировались системы автоматизированного проектирования (САПР).

Наиболее представительными и широко используемыми из них являются следующие группы САПР:

• 1.    САПР для применения в отраслях общего машиностроения. Их часто называют машиностроительными САПР или системами M CAD (Mechanical CAD);

• 2.    САПР для радиоэлектроники: системы ECAD (Electronic C Ad) или EDA (Electronic Design Automation);

• 3.    САПР в области архитектуры и строительства.

• 4.    Комплексные (интегрированные) САПР, состоящие из совокупности подсистем различных видов. Характерными примерами комплексных САПР являются CAE / CAD/ САМ 5 -системы в машиностроении или САПР БИС. Так, САПР БИС включает в себя СУБД и подсистемы проектирования компонентов, принципиальных, логических и функциональных схем, топологии кристаллов, тестов для проверки годности изделий. Для управления столь сложными системами применяют специализированные системные среды.

Большой популярностью среди инженеров исследователей сегодня пользуется универсальная программная система конечноэлементного (МКЭ) анализа ANSYS, существующая и развивающаяся на протяжении послед-

5 CAD (англ. computer - aided design) - система автоматизированного проектирования. САЕ (англ. Computer - aided engineering) - автоматизированное проектирование; (англ. Computer — aided manufacturing) - автоматизированная система, либо модуль, предназначенный для подготовки управляющих программ для станков с ЧПУ. Под термином понимаются как сам процесс компьютеризированной подготовки производства, так и программно-вычислительные комплексы, используемые инженерами-технологами. В ряде зарубежных источников устанавливается определённая соподчи-ненность понятий CAD, CAE, CAM. Термин CAE определяется как наиболее общее понятие, включающее любое использование компьютерных технологий в инженерной деятельности, включая CAD и CAM.

них 30 лет. Она является довольно популярной у специалистов в сфере автоматизированных инженерных расчётов и КЭ решения линейных и нелинейных, стационарных и нестационарных пространственных задач механики деформируемого твёрдого тела , а также механики конструкций (включая нестационарные геометрически и физически нелинейные задачи контактного взаимодействия элементов конструкций), задач механики жидкости и газа, теплопередачи и теплообмена, электродинамики, акустики, механики связанных полей и др.

Предлагаемые фирмой ANSYS Inc. средства численного моделирования и анализа совместимы с некоторыми другими пакетами, в частности система ANSYS сопрягается с С- системами      NX, CATIA, Pro/ENGINEER,

SolidEdge, SolidWorks, Autodesk Inventor и некоторыми другими.

На рисунках 4 – 7 приведены графические интерпретации решения различных инженерных задач, выполненных с участием автора в среде ANSYS, которые отчасти иллюстрируют широкие возможности применяемой совместно со средствами CAD системы.

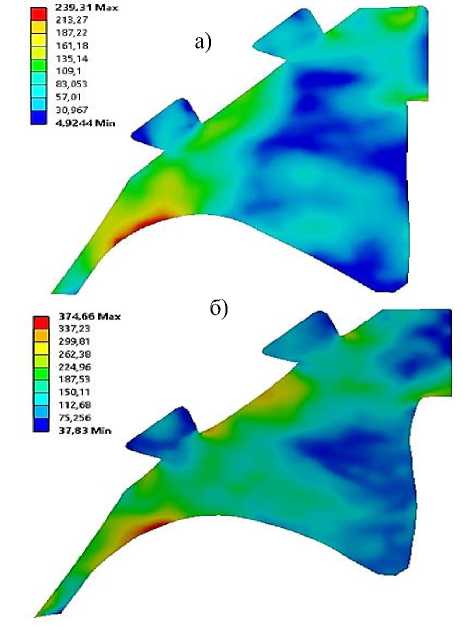
Рисунок 4 – Интенсивность напряжений обтюри- рующего устройства, деформирующегося при давлении 500 МПа, построенные в ANSYS с использованием различных уравнений состояния: а) –Ми-Грюнайзена; б) –Муни-Ривлина.

Источник [7]

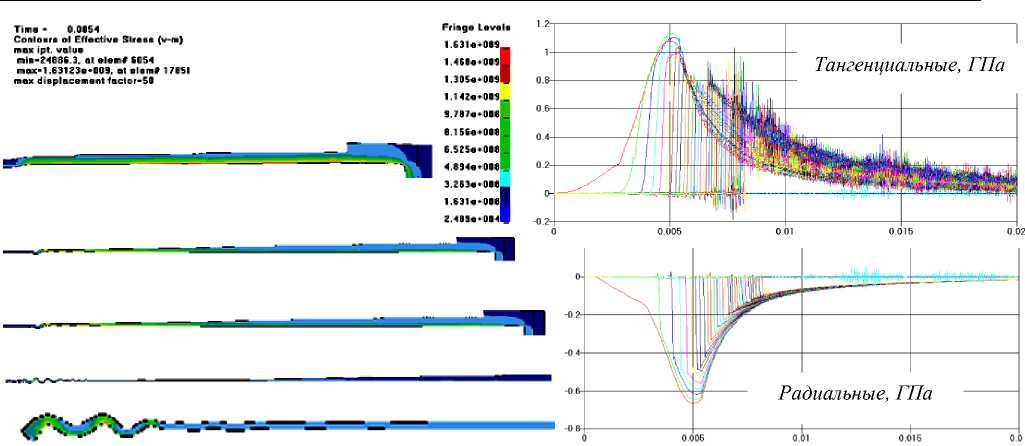
Time -   0.0004

б)

Рисунок 5 - Результаты анализа нагружения трубы динамическим импульсом [8]: а) — картина деформирования; б) - к омпоненты напряжений для внутренних точек трубы от времени в с

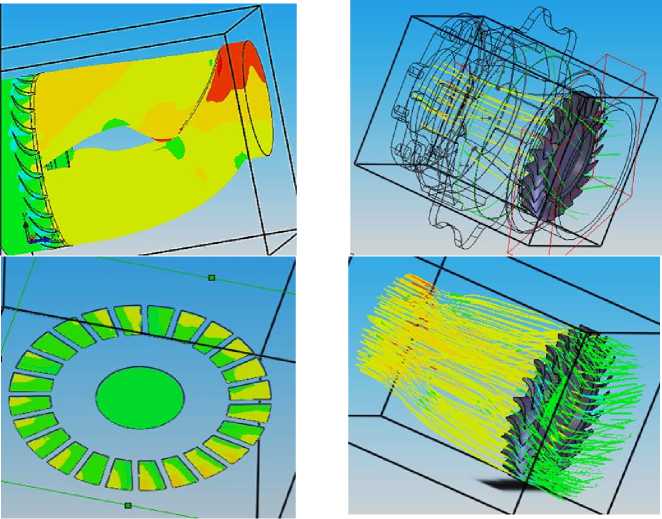
а)                                                б)

Рисунок 6 — Результаты анализа движения воздуха в системе турбонаддува двигателя внутреннего сгорания [9]: а) — распределение давления газов на по поверхности канала и на выходе соплового венца; б) — направления движения потока

У инженеров конструкторов наибольшей популярностью пользуется SolidWorks как средство для автоматизации работ на этапах конструкторской и технологической подготовки производства, обеспечивающее разработку изделий любой степени сложности и назначения. Система SolidWorks стала первой САПР, поддерживающей твердотельное моделирование для платформы Windows и на сего- дняшний день является едва ли не самым удобным программным средством, используемым в качестве препроцессора для решения многих инженерных задач САЕ — системами(см. пример на рис.8). Современные пакеты SolidWorks имеют собственную интегрированную среду решения широкого круга задач, присущих более тяжелым пакетам, таким как ANSYS Workbench, Autodesk Inventor и др.

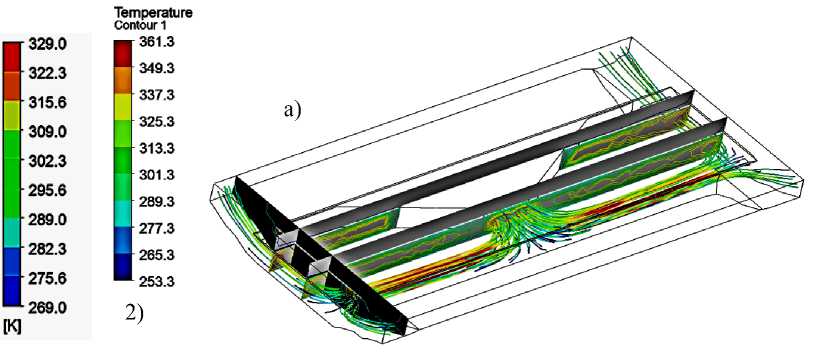
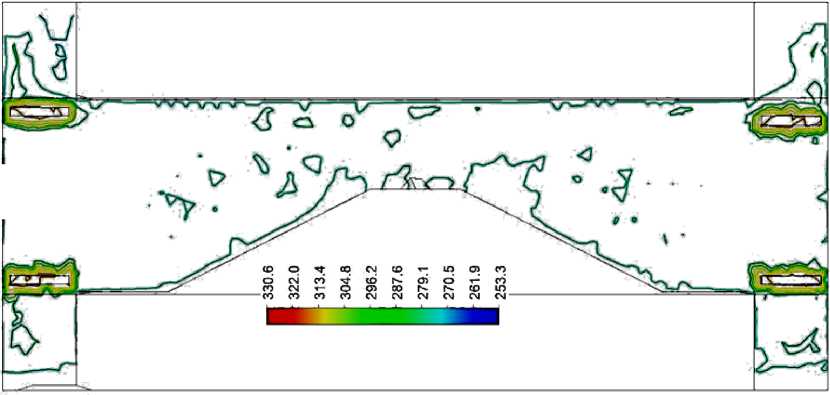
Рисунок 7 - Анализ тепломассопереноса в подогреваемом подземном переходе среде ANSYS Workbench; интерпретация в постпроцессоре CFD — Post [10]: а - линии тока; б - карта температур в продольной вертикальной плоскости перехода; в – карта температур в горизонтальной плоскости перехода; 1 – подогревателя мощностью 4,8 кВт; 2 – подогревателя мощностью 9,6 кВт))

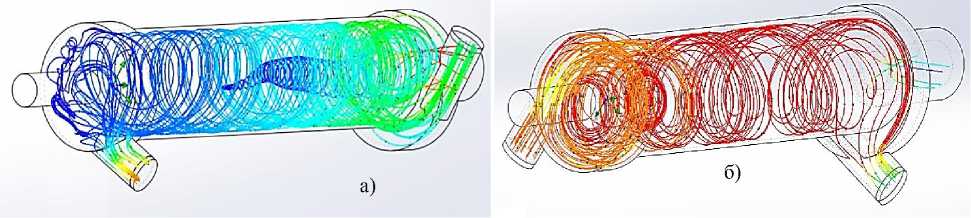
Рисунок 8 - Формирование потока в трубе Ранка-Хильша, рассчитанные в среде

SolidWorks / FloSimulation [11] : а) - скорости; б) - температуры

Численное моделирование функционирования сложной системы, описываемой происходящими в ней различными физическими процессами (мультифизическими) называют имитационным моделированием. В процессе имитационного моделирования часто используется метод статистического моделирования (Монте-Карло), состоящий в получении оценок вероятностных характеристик и применяющийся для имитации процессов, происходящих в системах, внутри которых есть источник случайности или которые подвержены случайным воздействиям [12]. Суть имитационного моделирования заключается в имитации процесса функционирования системы во времени, с соблюдением таких же соотношений длительности операций как в системе оригинале. При этом имитируются элементарные процессы, составляющие явление; сохраняется их логическая структура и взаимная связь, последова- тельность (или одновременность) протекания во времени, случайные факторы и воздействия. Результатом имитационного моделирования является получение оценок характеристик системы.

На рисунке 9 представлены результаты моделирования рассеяния баллистических параметров при стрельбе артиллерийской системы (АС) [13]. Моделирование проводится на совокупности детерминированных моделей взаимосвязанных процессов, происходящих при выстреле как в стволе, так и на траектории, реализованном в разработанной автором программной среде INNER. Причем в качестве исходных данных выступают параметры АС имеющие стохастический характер вследствие технологических разбросов размеров, формы и отклонения поверхностей, либо связанные с условиями эксплуатации, причем различающиеся законами распределения.

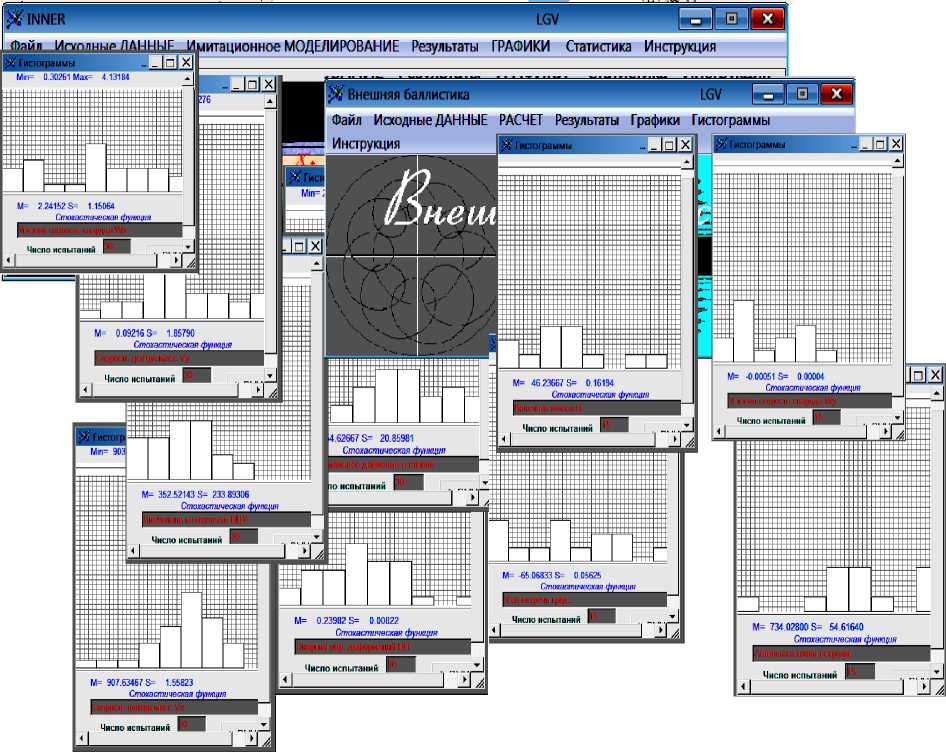
Рисунок 9 - Результаты моделирования рассеяния баллистических параметров [12]

Задача оценки функционирования сложных технических систем по различным критериям, соответствующим разным по физи- ческому содержанию процессам, сводится к задаче математического программирования, причем в основном нелинейного. В целом такая задача является достаточно сложной для численной реализации [14]. Возможности ее упрощения и заключаются в соблюдении принципов иерархии моделей, построенных на различных классах и их декомпозиции в любом из классов: причем как по физическому их содержанию, так и по элементам конструкции узлов, агрега- тов и всей машины в целом [15]. При этом перечисленную совокупность показателей основных процессов и критериев оценки можно определить с учетом принципов иерархии на совокупности математических моделей, представленной таблицей 1.

Таблица 1 – Иерархические классы математических моделей оценки функционирования технических систем

№ п/п	Обозначение класса	Содержание и объем класса	Совокупность математических моделей, параметров, свойств.	Показатели эффективности
1	Техническая система	Надежность технических систем и стабильность производства	Прогнозирование качественных показателей продукции, экономической эффективности производства.	Объем продукции. Рентабельность производства.
2	Технологический комплекс	Технологическая машина, рабочий процесс, заготовка изделия	Имитационные статистические модели взаимосвязанной совокупности процессов, происходящих при выпуске продукции	Качество продукции. Стабильность производственных процессов. Безотказность долговечность, ресурс выпускаемых изделий и др.
3	Технологическая машина	Электропривод, система управления, механическая часть, рабочий орган	Динамика поступательного и вращательного движения, силовое взаимодействие, координаты положения и др.	Экономическая эффективность, коэффициент полезного действия (КПД), ресурс, характеристики рабочего процесса, объем производимой продукции, качество технологической операции
4	Агрегат	Электродвигатель, редуктор, муфта, исполнительный орган	НДС, контактное силовое и тепловое взаимодействие между элементами.	КПД, показатели надежности и эффективности
5	Деталь	Вал, зубчатое колесо, инструмент и др.	НДС, формоизменение, характеристики жесткости.	Уровни прочности, стойкости, долговечности, усилия при формоизменении

Т.о., исходя из принципа декомпозиции, все основные конструктивные схемы сложной технической системы, несмотря на их разнообразие можно свести к конечной совокупности взаимосвязанных элементов, к которым отнесем: электропривод, система управления, механическая часть, рабочий орган и др. Каждый из перечисленных элементов может рассматриваться как подсистема, функционирование которой определено на основании отдельных частных математических моделей в системе "агрегат ". В частности на этом уровне могут быть определены математические модели НДС, контактного силового и теплового взаимодействия между элементами агрегата, определены их качественные характеристики по критериям допустимых уровней: КПД, показателей надежности и эффективности. Далее уже на уровне самого нижнего класса " деталь" проводится оценка уровней прочности, стойкости, долговечности.

Переход с одного класса модели на другой при анализе имитационной модели в любом случае предполагает итерационное решение всей совокупности моделей с уточнением на каждой итерации граничных и начальных условий как при переходе к нижнему, так и к более высокому классу.

На сегодняшний день компьютерное моделирование является важным инструментом во всех областях человеческой деятельности. Современные программные продукты облада- ют развитыми интерфейсами и постпроцессорами, которые предназначены для быстрой адаптации пользователя, и у него есть возможность уделить больше внимания проведению имитационных экспериментов и анализу их результатов. Перспективными направлениями развития имитационного моделирования представляются следующие области:

– реализация и оптимизация результатов имитационных экспериментов;

– имитационное моделирование функционирования сложных систем;

– имитационное моделирование реальных производственных процессов;

– имитационное моделирование системы одновременно с ее функционированием, что позволит предсказывать поведение системы;

– имитационное моделирование функционирования объектов управления, что позволит изучать разные алгоритмы управления объектами и др.