Имитационное моделирование в задачах оценки остаточной долговечности элементов конструкций

ВЕСТНИК ПНИПУ. МЕХАНИКА № 5, 2024PNRPU MECHANICS BULLETIN

Настоящий обзор основан на положительном опыте, который накоплен коллективом сотрудников лабораторий ФИЦ Казанский научный центр РАН в порядке обоснования состоявшихся в практике эксплуатации вращающихся дисков турбомашин в авиации и станционной энергетике конструктивно-технологических решений [1–17]. Этот опыт не ограничивается настоящими результатами и в соответствующих публикациях коллектива авторов представлены решения научных проблем, связанных с эксплуатацией и проектированием трубопроводов, панелей обшивки фюзеляжа, гидроцилиндров и т.д. [18; 19].

В настоящее время проектирование компонентов паровых турбин станционной энергетики и газотурбинных двигателей (ГТД) гражданской авиации становится очень сложным из-за высоких температур, комплексных механических нагрузок, коррозионной среды и длительных прогнозируемых сроков службы. Эксплуатация узлов паровых турбин и авиационных двигателей характеризуется достижением предельных параметров и условий. Необходимость обеспечения длительного срока службы обусловливает применение концепции допускаемой повреждаемости, основанной на анализе состояния критических зон элементов конструкций. Условия нагружения вращающихся дисков турбомашин предопределяют зарождение и развитие усталостных трещин в критических зонах в условиях многоосного напряженно-деформированного состояния, высоких температур и коррозионных сред. Состояние этих критических зон характеризуется нелинейным деформированием, когда эквивалентные напряжения по Мизесу превышают предел текучести материала при соответ- ствующей температуре в условиях одноосного растяжения. Эти обстоятельства стимулируют разработку новых моделей роста усталостных трещин, которые все чаще используются в качестве инженерных инструментов для оценки остаточной долговечности элементов конструкций. Предполагается реализация технологии субкомпонентных испытаний и подходов континуальной механики повреждений сплошных сред, а также методов механики упругопластического разрушения к оценке несущей способности вращающихся дисков турбомашин. Прогнозирование роста усталостных трещин в критических зонах вращающегося диска при нестационарном термомеханическом нагружении является одной из составляющих стратегии эксплуатации по условиям допускаемой повреждаемости на основе диагностики индивидуального технического состояния элементов конструкций.

Одним из инженерных инструментов достижения этих целей могут быть подходы по имитационному моделированию. Подобные подходы можно разделить на две основные стратегии. Первая представляет собой испытания образцов или имитационных моделей, которые непосредственно вырезаны из рассматриваемых критических зон конструкций. В этом случае имитационная модель содержит эксплуатационные повреждения, накопленные в критических зонах, и сохраняет состояние внешней поверхности при достигнутом уровне долговечности. Вторая стратегия требует проектирования и изготовления специальных имитационных моделей и испытательных стендов. В некоторых случаях имитация применяется для калибровки и проверки усовершенствованных подходов к моделированию роста усталостных трещин и прогнозированию срока службы, поскольку очень сложно воспроизвести на стандартных испытательных образцах напряженно-деформированное состояние, возникающее в процессе эксплуатации реальных вращающихся дисков турбомашин. Проектирование и изготовление имитационных моделей может быть осуществлено из того же материала, что и диск турбины или компрессора, в строгом соответствии с технологией их изготовления. Основной недостаток испытаний полноразмерных конструкций состоит в высокой стоимости и длительности проведения испытаний, отсутствии возможностей наблюдения за развитием дефектов, а также низкой статистической достоверности результатов испытаний. Подходы имитационного моделирования свободны от большинства подобных ограничений. Главным преимуществом имитационного моделирования в ряде случаев является замена дорогостоящих и длительных испытаний натурных конструкций. Как правило, имитационное моделирование представляет собой комбинацию расширенных экспериментальных и параметрических численных исследований.

Принципы имитационного моделирования

Эволюция имитационного моделирования состояла в первоначальном использовании стендовых испытаний полноразмерных дисков. В этом ряду особое положение занимает метод испытаний невращающихся дисков компрессора ГТД на электрогидравлическом стенде [20]. Силовая схема этого стенда включала гидроцилиндры, расположенные на периферии кольцевой рамы, количество которых соответствовало числу лопаток в выбранной ступени компрессора (рис. 1). Каждый гидроцилиндр имел нагружающую тягу с законцовкой, полностью воспроизводящей геометрию хвостовика лопатки в соединении с диском типа «ласточкин хвост». Система управления стендом позволяла реализовать программируемые профили нагружения, эквивалентные типовым полетным циклам. Внешние поверхности диска были доступны для непосредственных измерений процессов развития трещин в нескольких замковых соединениях одновременно.

К очевидным преимуществам имитационных испытаний полноразмерного диска компрессора ГТД на электрогидравлическом стенде можно отнести следующие моменты:

• –    использование диска с сохранением технологической наследственности и поврежденности в критических зонах;

• –    оперативная оценка с точки зрения долговечности конструктивно-технологических изменений в проектировании и изготовлении дисков;

• –    возможность воспроизведения эксплуатационных условий и основных повреждающих факторов;

• –    статистически корректное экспериментальное обоснование полученных численных результатов;

  – относительно низкая стоимость стендовых испытаний по отношению к разгонным испытаниям дисков в составе двигателя.

Рис. 1. Электрогидравлический стенд для испытаний дисков компрессора ГТД

Fig. 1. Electric and hydraulic test bench for compressor disks of GTE

Существенным ограничением тиражирования данного метода имитационного моделирования являются возможности производителей подобного уникального испытательного оборудования.

Основные принципы моделирования применительно к дискам турбин энергетического машиностроения и авиационных газотурбинных двигателей сформулированы авторами [3; 7; 13; 16]. Первым из них является принцип подобия и воспроизведения состояния критической зоны элемента конструкции на имитационной модели. Процесс разрушения всегда носит локальный характер и инициируется в зонах концентрации напряжений и деформаций. Поэтому начальным этапом имитационного моделирования является определение локального напряженно-деформированного состояния элемента конструкции для эксплуатационных условий нагружения. В результате определяются положение интересующей области и критические размеры дефектов, приводящих к разрушению. Тем самым устанавливается состояние и размеры области, которую необходимо воспроизвести на имитационной модели. Обязательным условием моделирования является сохранение геометрических параметров зоны концентрации напряжений конструкции на имитационной модели. В тех случаях, когда имитационная модель вырезается из натурной конструкции после эксплуатации, необходимо сохранение состояния поверхности с накопленными повреждениями в критической зоне. Затем с помощью итерационного численного параметрического исследования устанавливаются размеры имитационной модели, включая контуры конструктивного концентратора напряжений, и условия ее нагружения. Эти условия воспроизводят максимальные напряжения и деформации, профиль нагружения (частоту, время выдержки, асимметрию цикла), изменения температуры и воздействие агрессивной среды. Задаваемые схема и профиль нагружения должны обеспечить воспроизведение координат появления начального дефекта и последующей траектории развития трещины в имитационной модели, как в состоявшихся случаях эксплуатационных разрушений элементов конструкций.

Современный уровень испытательного оборудования позволяет с определенным успехом реализовать эти требования при расчетах и испытаниях имитационных моделей. В большинстве случаев испытания имитационных моделей могут быть осуществлены на стандартных установках растяжения-сжатия или кручения при дополнительном оснащении устройствами силовых потоков, климатических и вакуумных камер, катушек индукционного и печей конвективного нагрева. В ряде случаев необходимо проектирование и изготовление специализированных испытательных установок, воспроизводящих многоосное термомеханическое нагружение. Таким образом, подход имитационного моделирования должен воспроизводить условия нагружения, процессы накопления и роста повреждений, а также разрушения реального конструктивного элемента.

Цель данного исследования – иллюстрация эффективности подхода имитационного моделирования для обоснования конструктивно-технологических решений модификации и оценки характеристик остаточной долговечности элементов конструкций паровых турбин и авиационных двигателей. Представленные примеры решений сформированы по сочетаниям условий нагружения и типов повреждений в эксплуатации.

Моделирование развития трещин в диске компрессора ГТД при смешанных формах разрушения

Первый пример относится к эксплуатационному повреждению диска компрессора низкого давления авиационного ГТД уголковой наклонной трещиной в радиусном сопряжении стенки и донышка паза замкового соединения типа «ласточкин хвост» (рис. 2). Диск изготовлен из титанового сплава ВТ3-1. Цель имитационного моделирования состояла в обосновании конструктивнотехнологических решений по изменению профиля паза и обработки поверхности методами пластического деформирования. Для оценки и обоснования решений был спроектирован и изготовлен электрогидравлический стенд, который позволяет проводить испытания полноразмерного диска по заданной программе (см. рис. 1).

Рис. 2. Эксплуатационное повреждение в замковом соединении диска компрессора ГТД

Fig. 2. Operation damage in a GTE compressor disk locking attachment

b

c

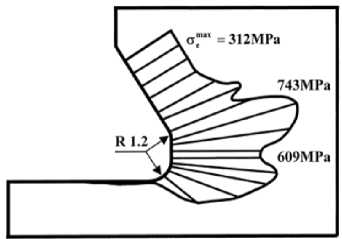
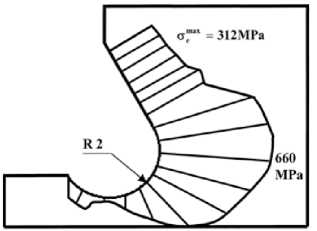
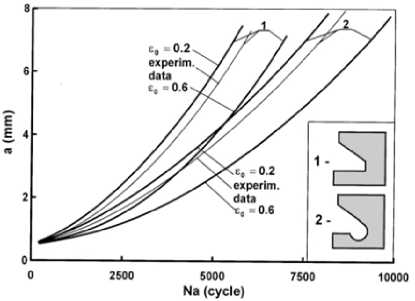
Рис. 3. Сравнение исходного ( а ) и модифицированного ( b ) вариантов исполнения паза по долговечности на стадии роста трещины ( c )

Fig. 3. Comparison of the original ( a ) and modified ( b ) versions of the key slot at the crack growth life stage ( c )

Рассматривалось обоснование изменения зоны сопряжения наклонной стенки и донышка паза за счет формирования одного общего радиусного перехода с одновременным удалением объема поврежденного материала на прилегаемой поверхности (рис. 3, а, b). Проведенные численные расчеты конкурентных вариантов показали, что предлагаемое изменение конфигурации паза приводит к снижению пика действующих напряжений на 12–15 %. На этом основании были изготовлены несколько дисков компрессора предлагаемой конфигурации замкового соединения, поверхность которых была обработана различными методами поверхностного пластического деформирования. Эти диски были испытаны на электрогидравлическом стенде (см. рис. 1) по программе циклического нагружения, эквивалентной типовому полетному циклу. По результатам испытаний были получены кривые долговечности Nfi для исходного и модифицированного исполнения диска компрессора, которые приведены на рис. 3, с.

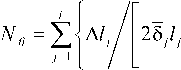
'JK-j h ^K^

^ 4Jf sfE 5 j ?

В этих уравнениях l j и 5 j длина трещины и ее приращение, ст _n , j _th номинальные и пороговые напряжения, ст _f, s _f предельные напряжения и деформации, K_f , NK_th - предельные и пороговые коэффициенты интенсивности напряжений.

По результатам испытаний установлен оптимальный вариант сочетания изменения геометрии и технологического воздействия на состояние поверхности, который обеспечил двукратное увеличение остаточной долговечности диска компрессора. В дополнение к экспериментальным данным были выполнены прогнозные расчеты по модели (1), подробное изложение которой представлено в работе авторов [1]. Сопоставление расчетных и экспериментальных данных, приведенных на рис. 3, с , показывает их взаимное соответствие и является необходимым звеном в обосновании принимаемых решений.

Имитационное моделирование с использованием полноразмерных дисков компрессора обладает существенными преимуществами по отношению к разгонным испытаниям в составе двигателя, однако ограничено необходимостью создания уникальных комплексов при изменении конфигурации рассматриваемого изделия. Более перспективным с точки зрения снижения затрат и повышения статистической достоверности является подход по имитационному моделированию состояния критических зон элемента конструкции. Ниже представлено изложение этого подхода в приложении к рассматриваемому диску компрессора авиационного ГТД, что является логическим продолжением стендовых испытаний.

Для реализации подхода критических зон в первую очередь необходимо установить напряженно-деформированное состояние (НДС) диска в эксплуатации с целью его последующего моделирования. Для этого выполнены численные расчеты в трехмерной нелинейной постановке с привлечением МКЭ, которые позволили охарактеризовать общее (рис. 4) и локальное (рис. 5) НДС в зоне повреждения рассматриваемого элемента конструкции. Для характеристики общего НДС диска компрессора использованы показатели двухосности и трехосности действующих напряжений согласно уравнениям (2)

n = Jrr /стее, h = ст№/(3^/2 ■ ^^ ) (2)

в которых стrr, стее - компоненты радиальных и окружных напряжений, стkk - гидростатические напряжения, Sij – девиатор тензора напряжений. Из представленных на рис. 4 распределений по радиусу диска коэффициентов двухосности и трехосности напряжений был сделан вывод о необходимости обеспечения многоосного напряженного состояния в имитационной модели для корректного воспроизведения НДС диска в эксплуатации. Анализ зон концентрации напряжений и деформаций в диске (см. рис. 5) показал существенное влияние угла наклона паза к оси вращения, которое должно быть воспроизведено в имитационной модели с сохранением всех геометрических размеров.

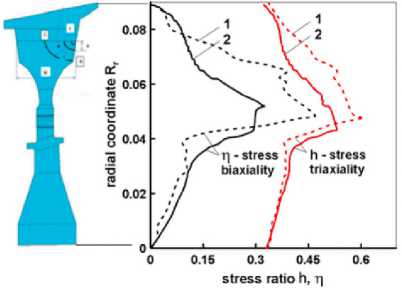
Рис. 4. Радиальные распределения коэффициентов двухосности и трехосности напряжений в диске компрессора

Fig. 4. Radial distributions of the stress biaxiality and triaxiality factors in the compressor disk

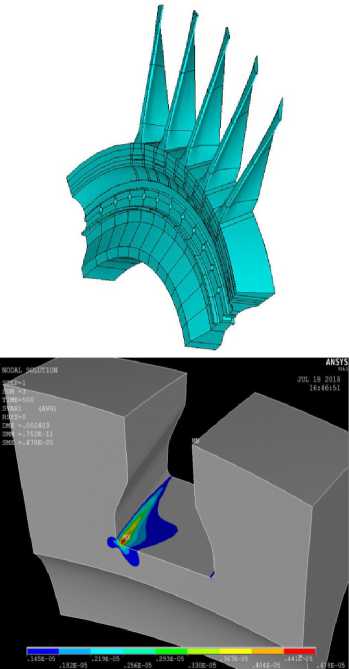
Рис. 5. Концентрация напряжений в остром углу паза обода диска компрессора

Fig.5. Stress concentration in the sharp corner of the key slot of the compressor disk rim

Установленным требованиям соответствовала имитационная модель критической зоны диска, показанная на рис. 6, a. Циклическое нагружение модели осуществлялось системой сил во взаимно перпендикулярных направлениях, где центробежная нагрузка передавалась через имитатор хвостовика лопатки. Для проведения имитационных моделей при двухосном нагружении был спроектирован и изготовлен электрогидравлический стенд с современной системой управления и широким диапазоном вариации фаз нагружения (рис. 6, b).

В результате серии итерационных численных расчетов была определена конфигурация двухосно нагруженной имитационной модели, которая полностью воспроизводила геометрию критической зоны замкового соединения хвостовика лопатки с диском компрессора (рис. 7, с ).

b

а

Рис. 6. Электрогидравлический стенд для двухосных испытаний имитационной модели

Fig. 6. Electric and hydraulic rig for biaxial testing of the simulation model

b

a

Рис. 7. Сопоставление траекторий роста трещин и поверхностей разрушения в диске компрессора ( a , b ) и имитационной модели ( с , d )

d

Fig. 7. Comparison of the crack growth paths and fracture surfaces in the compressor disk ( a , b ) and the simulation model ( c , d )

Проведенные испытания по эквивалентному полетному блоку переменных амплитуд нагружения показали полное соответствие траекторий и поверхностей разрушения в натурном поврежденном в эксплуатации диске компрессора (рис. 7, а , b ) и имитационной модели (рис. 7, с , d ). Данная ситуация позволила выполнить серию экспериментов по тщательному изучению процессов развития трещин и оценке остаточной долговечности в терминах механики деформирования и разрушения. Эксплуатационное повреждение диска представляло собой наклонную трещину с последовательными стадиями перехода от поверхностного к сквозному дефекту с криволинейным фронтом. Подобное повреждение относится к наиболее сложным трехмерным задачам, которые характеризуются наличием всех трех форм деформирования и разрушения. Для интерпретации экспериментальных данных был введен эквивалентный коэффициент интенсивности напряжений (КИН)

Keqv (0*) = (1 + V) cos2 |д Jx

( 1 _-v) K I² ( 1 + cos 0 * ) - 4 K I K II sin 0 * + 2    + K 2 ( 5 - 3cos 0 * )

(1 - v)

K 2 | sin — + sin — 0 * | + 4 KK„ cos — 0 ' -

• ¹    ^ 2        2 J ^{1 11} 2

2• 30*■ 0'

- K  3sin — 0 - 5 sin

111         22

+

• 2    .0'1„

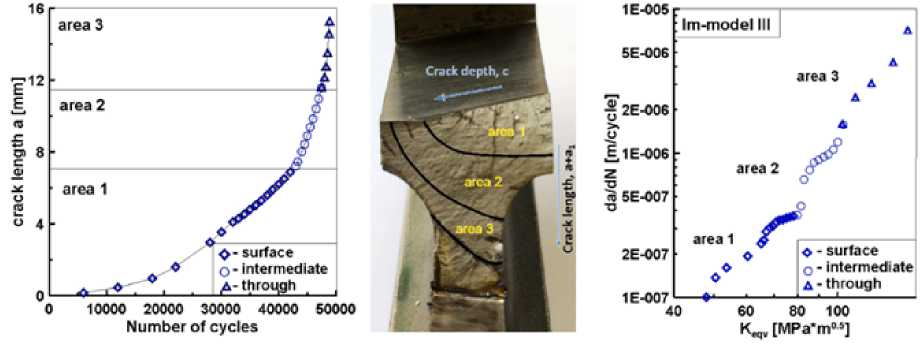
+KIII siny= 0, в котором θ* – угол девиации фронта трещины, КI, КII, КIII – КИН для форм отрыва, сдвига и среза соответ- ственно. Полученные результаты по характеристикам долговечности и скорости развития трещин (рис. 8) позволили установить стадийность процессов и доминирующие механизмы разрушения, которые были обобщены в рекомендациях по безопасной эксплуатации дисков компрессора авиационного ГТД [13].

Моделирование развития трещин в диске турбины ГТД при переменной амплитуде нагружения

Следующий пример имитационного моделирования относится к оценке характеристик сопротивления разрушению диска турбины авиационного двигателя (рис. 9, a ) с эксплуатационным повреждением на контуре отверстия под стяжной болт между ступенями (рис. 9, b ). Диск турбины изготовлен из жаропрочного сплава ЭИ-698. Анализ НДС диска для эксплуатационных условий нагружения подтвердил, что поверхность отверстия является зоной концентрации напряжений и накопления повреждений (рис. 9, с ). Следуя принципам сохранения геометрии критической зоны, было принято решение вырезать имитационные модели непосредственно из ступичной части диска турбины (рис. 10, a ). Таким образом, имитационная модель сохраняла внешние обводы и сечения натурной конструкции (рис. 10, b ). Задача состояла в выборе плеча приложения внешней силы при нагружении модели по схеме внецентренного растяжения.

Выполненная серия параметрических численных расчетов позволила установить блочную последовательность приложения нагрузки к имитационной модели для достижения соответствия распределений напряжений на пути развития трещины в натурном диске турбины [14–16].

a                                          b

Рис. 8. Диаграммы долговечности ( а ) и скорости роста трещины ( b ) в имитационной модели диска компрессора

Fig. 8. Fatigue life diagrams ( a ) and crack growth rate ( b ) in the simulation model of the compressor disk

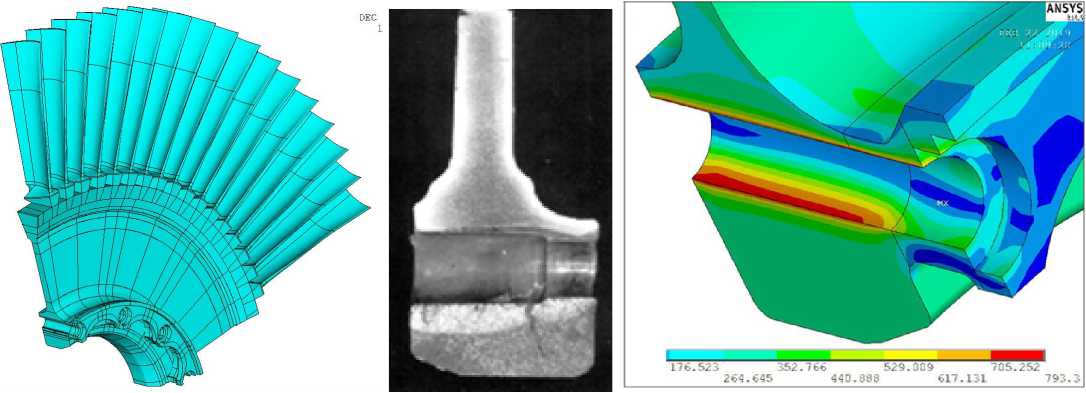
а                                b                                 с

Рис. 9. Эксплуатационное повреждение поверхности отверстия в диске турбины

• Fig. 9.    Operation damage to the surface of the hole in the turbine disk

  

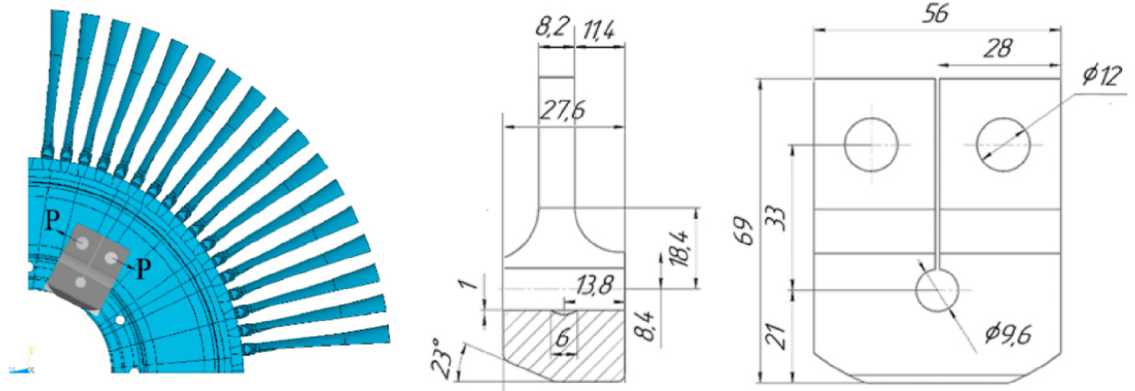
  a                                                   b

  Рис. 10. Имитационная модель диска турбины ГТД

  
  

• Fig. 10.    Simulation model of a GTE turbine disk

  

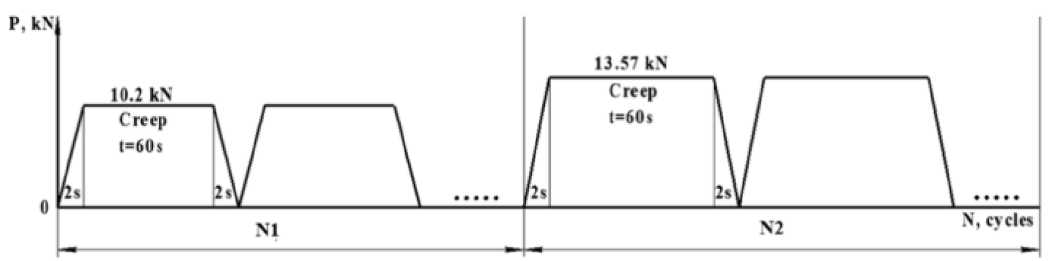
  Рис. 11. Блочный профиль нагружения при взаимодействии усталости и ползучести

  Fig. 11. Block loading profile for fatigue-creep interaction

  
  

Кроме того, моделирование полетного профиля нагружения диска привело к необходимости формирования трапециевидного цикла деформирования с площадкой выдержки при максимальной нагрузке в условиях повышенной температуры (рис. 11). Подобный профиль нагружения имитационной модели классифицируется как взаимодействие усталости и ползучести.

Для проведения испытаний имитационных моделей при программно-блочном циклическом нагружении был сформирован экспериментальный комплекс с печью нагрева при высокой температуре и регистрацией роста трещины методом разности электрических потенциалов (рис. 12).

Предполагаемая интерпретация экспериментальных данных по скорости роста трещин при высокой температуре с выдержкой под нагрузкой обусловила необходимость использования для этих целей коэффициента интенсивности напряжений при ползучести [21]:

K cr =

1 ( C * ^ " cr + 1 ^ 0 1 B^L )

где L характерный размер тела с трещиной, B и ncr константы Нортона, С* - интеграл при ползучести, с0 предел текучести материала при соответствующей темпе- ратуре, Incr – управляющий параметр НДС для состояния ползучести в области вершины трещины

С ( 9 , t , n„ ) = J”        ( 6 e ) n r ⁺ 1 cos 9 d 9 -

^-n n_cr + Г   '

-

-n

, - ( 5 u„    д (du_r A)      | du_r

¹ ° rr l —--1 I I-⁰ r ₉I — +

^ дt   д9 ^ дt J J     ^ дt sin 9 d 9-

д ( д й ₉ аеГдТ

1 Г дй _r

° rr + n_cr + 1 ^      д t

°ra—⁹ cos 9 d 9 r ⁹ д t J

В уравнении (6) °_е, ( ° j ) - безразмерные эквивалентные напряжения, ( д й " /д t ) - скорость изменения компонент перемещений во времени по угловой координате. На основе нелинейного коэффициента интенсивности напряжений (6) с использованием имитационной модели диска турбины была дана сравнительная оценка характеристик циклической трещиностойкости для условий гармонической усталости при нормальной и повышенной температуры, а также взаимодействия усталости и ползучести (рис. 13).

Важными для практических приложений стали установленные факты формирования общей диаграммы циклического разрушения для возрастающей последовательности нагрузок блочного профиля циклического деформирования и различия в скорости роста трещин на поверхности имитационной модели и в наиболее глубокой точке криволинейного фронта трещины.

Наиболее сложной при реализации в процессе испытаний является характерное для авиационных двигателей эксплуатационное состояние термомеханического нагружения с синфазным или противофазным одновременным циклическим изменением механической нагрузки и температуры. Проведение подобных экспериментов потребовало создания уникального испытательного комплекса с добавлением к электрогидравли-ческому стенду циклического нагружения катушек индукционного нагрева, форсунок воздушного охлаждения, керамических датчиков раскрытия трещины, пирометра и термопар (рис. 14). Объектом испытаний выступал специально спроектированный образец с односторонним боковым надрезом (см. рис. 14, d ).

a                                                   b

Рис. 12. Оборудование высокотемпературных испытаний ( a ) и поверхности разрушения имитационных моделей ( b )

Fig. 12. High temperature testing equipment ( a ) and fracture surfaces of simulation models ( b )

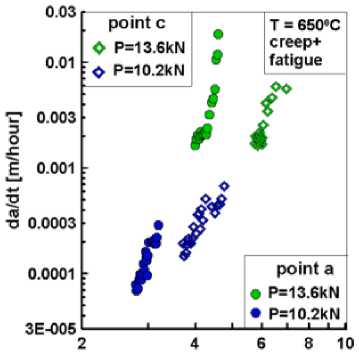
creep SIF

Рис. 13. Диаграммы усталостного разрушения для различных точек фронта несквозной трещины

Fig. 13. Fatigue failure diagrams for different points of the surface crack front

Рис. 14. Испытательное оборудование ( а–с ) и образец ( d ) для термомеханической усталости

Fig. 14. Test equipment ( a–c ) and specimen ( d ) for thermomechanical fatigue

Tempe ratute	Isothermal			Non-isothermal
Loading type	Fatigue harmonic fast isothermal	Fatigue harmonic slow isothermal	Creep + fatigue interaction isothermal	TMF in-phase	TMF out-ofphase (-180’)
£ и		IK . -~.....т,~-«_ ад	"I........Л.....Ju i:             :|	Я -5	* “я ад
		К    К    К J»	i        в я        mi	i и к И1 i« '
		ЮТИ	юты	юты	юти
ТГС]	23	400,650	400,650	400-650-400	400-650-400
ffHz]	1.0	0.017	0.014	0.014	0.014

Рис. 15. Профили нагружения и температуры для термомеханической усталости

a b                           c d

Fig. 15. Load and temperature profiles for thermomechanical fatigue

В отличие от рассмотренных выше вариантов имитационного моделирования, сосредоточенных на воспроизведении геометрии критической зоны в дисках ГТД, испытания при термомеханической усталости имеют основную цель оценки воздействия различных последовательностей изменения механических напряжений и температуры в сопряженном цикле деформирования. Авторами [17] сформированы и реализованы базовые программы испытаний на образцах из жаропрочного сплава ЭИ-698 (рис. 15), которые включали изотермическую усталость с разной частотой и температурой, взаимодействие усталости и ползучести при температуре 650 °С с выдержкой при максимальной нагрузке в течение 60 с, синфазную и противофазную термомеханическую усталость в цикле 60 с для нагрузки и температуры от 400 до 650 °С. Все эксперименты выполнены с использованием испытательного комплекса, показанного на рис. 14.

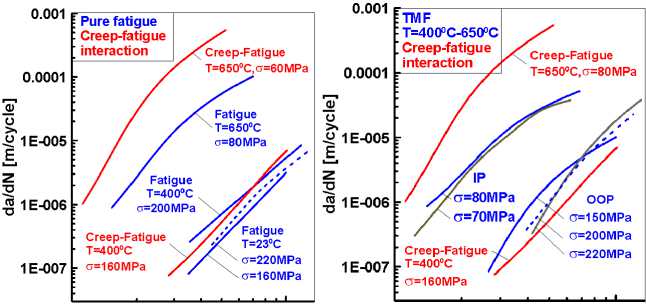
На рис. 16 представлена сравнительная оценка рассмотренных вариантов изотермического и неизотермического термомеханического нагружения в виде диаграмм усталостного разрушения в терминах упругих коэффициентов интенсивности напряжений, которые были получены для каждого испытанного образца в результате сопряженных мультифизических расчетов МКЭ

о ij

K i

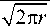
f j ( 0 ) ;

FEM

KI

vFEM (r, 0 = 0) r-1/2ёFFEM (r, 0 = 0)

где f ij ( 0 ) - безразмерные угловые функции компонент напряжений, K_i – упругие КИН, r , θ – полярные координаты, центрированные на вершину трещины. В результате анализа состоявшихся испытаний был установлен однозначный тренд снижения характеристик циклической трещиностойкости сплава ЭИ-698 по взаимному положению диаграмм усталостного разрушения при переходе от гармонической к термомеханической усталости и далее к взаимодействию усталости и ползучести при повышенной температуре. Увеличение скорости роста трещин в этой последовательности диаграмм наблюдалось более чем на порядок (см. рис. 16), на что было обращено внимание в соответствующих методических рекомендациях при оценках остаточной долговечности дисков турбин авиационных ГТД.

Оценка долговечности заклепочного соединения лопатки с диском паровой турбины

Методология имитационного моделирования, описанная выше, применена к оценке долговечности ротора паровой турбины ПТ-135/165-130. Накопление и рост повреждений в процессе эксплуатации диска паровой турбины, работающего в условиях циклического нагружения «пуск – останов», происходили на поверхностях отверстий в заклепочном соединении диска и лопатки (рис. 17).

В соответствии с принципами имитационного моделирования для анализа состояния критических зон, в которых в процессе эксплуатации накапливаются повреждения, по параметрам НДС была разработана и обоснована геометрия модели , удовлетворяющая следующим условиям:

– имитационная модель полностью воспроизводит конфигурацию сопряженных отверстий в выступе 23-й ступени диска паровой турбины;

– имитационная модель точно воспроизводит значения максимальных окружных напряжений на контуре отверстий для угловой координаты θ = 90°, возникающих в процессе эксплуатации в критической зоне натурного диска турбины;

– условия нагружения имитационной модели могут быть реализованы на стандартных машинах одноосного растяжения/сжатия.

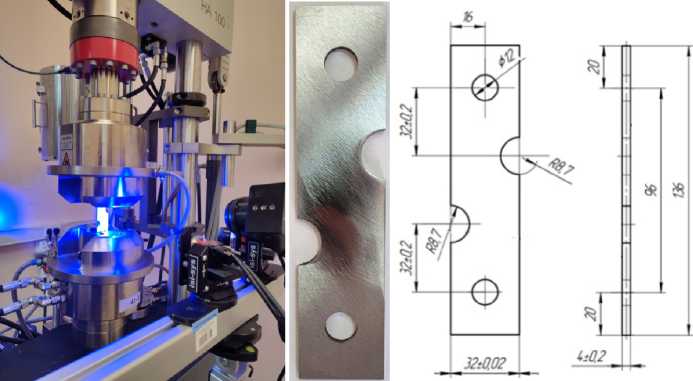
Одной из целей приложений имитационного моделирования в данном примере являлось обоснование расчетной модели прогнозирования долговечности ротора паровой турбины. Достижение этой цели предопределило необходимость четкой фиксации длительности стадий образования начального дефекта детектируемых размеров и развития последующей макротрещины до полного разрушения модели. В связи с этим было осуществлено непрерывное наблюдение и измерение состояния поверхности модели с использованием оптической системы цифровой корреляции изображений Isi-sys 3D-MicroDIC, оснащенной скоростной камерой высокого разрешения CameraIQ-7H-3 (рис. 18).

10      20     40 60 80100

elastic SIF К, [MPa*m05]

Рис. 16. Диаграммы усталостного разрушения для различных сочетаний усталости и ползучести

10      20      40  60 80100

elastic SIF K, [MPa*m05]

• Fig. 16.    Fatigue fracture diagrams for different combinations of fatigue and creep

  

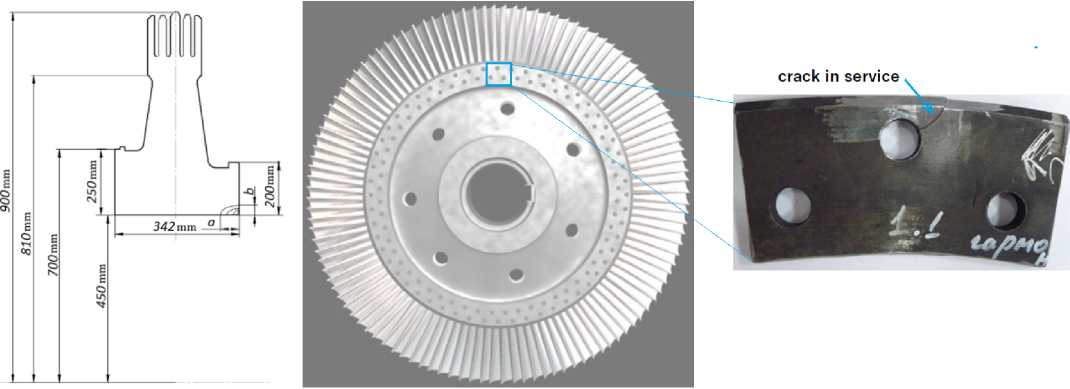
  Рис. 17. Диск паровой турбины с эксплуатационным повреждением

  
  

• Fig. 17.    Steam turbine disk with operation damage

  

  a                                          b

  Рис. 18. Оптическая система цифровой корреляции изображений ( а ) и имитационная модель обода диска паровой турбины ( b )

  
  

  Fig. 18. Optical digital image correlation system ( a ) and simulation model of steam turbine disk rim ( b )

  
  
  

  b

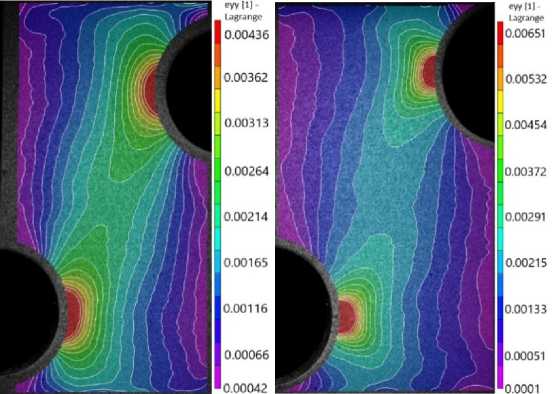
  Рис. 19. Поля деформаций в имитационной модели для различных уровней долговечности: a – первый цикл; b – 5750-й цикл; c – 6100-й цикл

  
  
  
  
  

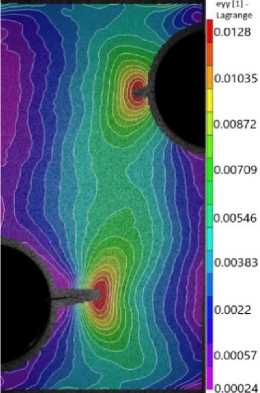
  Fig. 19. Strain fields in simulation model for different durability: a – first cycle; b – 5750 cycle; c – 6100 cycle

  
  

  По результатам состоявшихся измерений полей упругопластических деформаций при циклическом нагружении имитационных моделей (рис. 19) было установлено, что стадия образования начального дефекта размером 0,5 мм составляет 89 % от общей долговечности. Это обстоятельство было положено в основу формулировки модели прогнозирования малоцикловой долговечности с учетом функции накопления повреждений Lemaitre [22] и Armstrong-Frederick [23]

  
  

  R v

  
  
  
  

  ( 1 + u ) + 3(1 - 2 u )

  
  
  
  
  
  
  

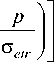
  ( “ ) '=«'Г^Т ) s

  
  

  ;

  
  
  
  

  - Y =

  
  

  ° e ■ Rv . 2 E (1 -ro ) ² ;

  
  
  
  

  где E – модуль упругости; ν – коэффициент Пуассона; r , s - параметры материала; ( ro ) - скорость накопления повреждений; ( у ) - скорость пластических деформаций; Y – энергия повреждения; R_v – параметр трех-осности; p - гидростатические напряжения; ст _etr -пробные упругие напряжения. Функция повреждения изменяется в интервале ω ∈ [0,1]: где ω = 0 соответствует неповрежденному материалу, тогда как ω = 1 принадлежит разрушению.

  
  

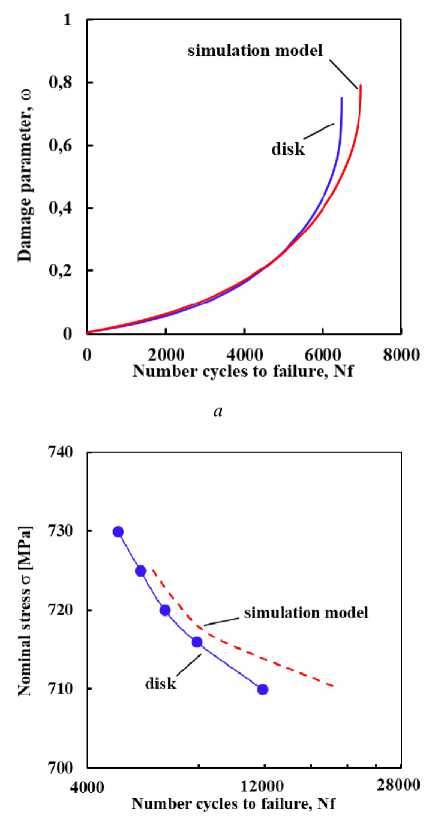
Верификация и валидация разработанного метода прогнозирования долговечности была осуществлена по результатам испытаний имитационной модели заклепочного соединения лопатки с диском паровой турбины. Далее в соответствии с этим методом были проведены прогнозные расчеты накопления повреждений и усталостной долговечности для натурного диска паровой турбины и имитационной модели, результаты которых представлены на рис. 20. Хорошее взаимное соответствие этих данных позволило рекомендовать разработанный метод к практическим приложениям в задачах оценки остаточной долговечности элементов конструкций.

b

Рис. 20. Накопление повреждений ( a ) и усталостная долговечность ( b ) в диске турбины и имитационной модели

Fig. 20. Damage accumulation ( a ) and fatigue life ( b ) in turbine disk and simulation model

Для завершения полноты оценки несущей способности диска паровой турбины с эксплуатационным повреждением была проведена оценка пути развития трещины от начального дефекта до полного разрушения проушины заклепочного соединения лопатки с диском.

а

b

c

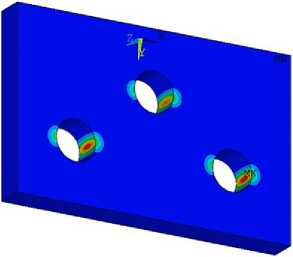
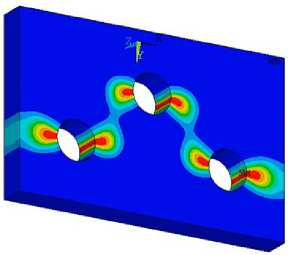
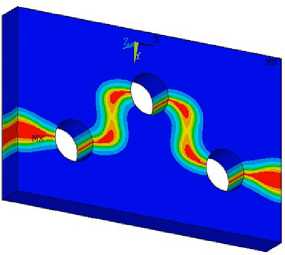
Рис. 21. Фазовые поля разрушения в проушине диска паровой турбины ( а–с )

Fig. 21. Phase fields of damage in lug of a steam turbine disk ( а–с )

Эти расчеты по прогнозированию траектории развития трещины выполнены с привлечением теории фазовых полей разрушения [24], в которой управляющим параметром является функция плотности энергии деформации

W u ) =f|[(1 -ф) 2 + k Me) + G c

2 l ф² + 2|уф ² H dv , (12)

где Ф ( e ) — плотность энергии деформации; G_C - критическая скорость выделения энергии или вязкость разрушения материала. Результаты расчетов с использованием этой функции приведены на рис. 21, которые иллюстрируют процесс формирования поверхностного дефекта в середине толщины проушины, а затем стадии взаимодействия и объединения полей повреждений для сопряженных отверстий в заклепочном замковом соединении.

Оценка конструктивных решений ремонтных технологий дисков паровой турбины

Подход имитационного моделирования показал свою эффективность не только на стадиях проектирования и эксплуатации элементов конструкций, но и в порядке выполнения регламентных работ по обслуживанию и ремонту изделий. Ниже приведены примеры состоявшихся конструктивно-технологических решений.

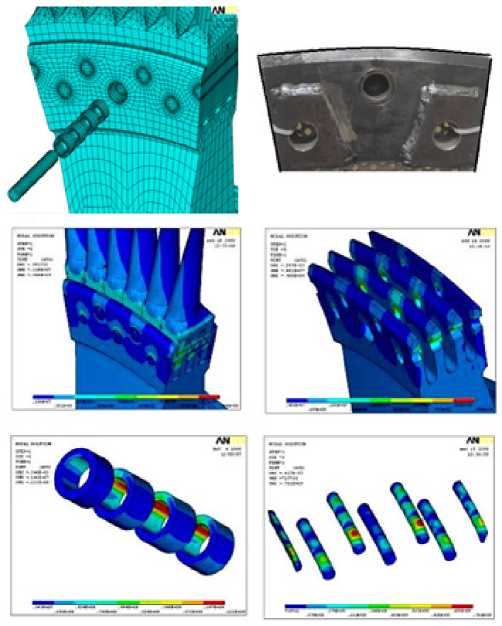
Проушины насадного диска паровой турбины были подвержены в эксплуатации повреждениям уголковыми несквозными трещинами, исходящими от контура отверстия под заклепку (рис. 22, a ). Размеры дефектов составляли 0,5–1 мм в отверстиях верхнего ряда заклепочного соединения лопатки с диском. Несмотря на то что диск является самым дорогим элементом паровой турбины, его эксплуатация с повреждением не допускалась, а полная замена не представлялась возможной. В связи с этим было принято решение о ремонтной технологии, в рамках которой в отверстиях с трещинами удалялся объем поврежденного материала, и его компенсация осуществлялась запрессовкой втулки в проушину диска (см. рис. 22, а ). Внутренний диаметр втулки соответствовал диаметру исходной заклепки, а наружный диаметр выбирался по условиям прочности внедренного элемента. Тем самым сохранялся диск турбины и пакет адаптированных лопаток. Состояние запрессованных втулок было оценено по результатам численного решения нелинейной контактной задачи для пакета «заклепка – втулка – проушина диска». В качестве параметров оценки НДС рассматриваемого пакета деталей использованы эквивалентные упругопластические напряжения и деформации

° e =-^2 ^/(^ ХХ -^ У У'+^ У г-^У+^Г-^^ ;^{(13) 6} e =^з² ((ь^-У^Г^^^ ■⁽¹⁴⁾

Для оценки допустимости предложенной технологической операции ремонта дисков паровой турбины с позиций долговечности были проведены сравнительные усталостные испытания имитационных моделей в виде секторов проушин с исходным и измененным конструктивом заклепочных отверстий.

При проведении усталостных испытаний была обеспечена эквивалентность напряженного состояния натурного диска и имитационной модели за счет разработанного приспособления реализации двухосного нагружения на стандартной испытательной установке (рис. 22, b ). Этого удалось достичь по результатам серии предварительных итерационных расчетов методом конечных элементов. Сравнительные испытания имитационных моделей показали, что проушины с запрессованной втулкой и в исходном состоянии имеют одинаковый диапазон долговечности, на основании чего были высказаны рекомендации по использованию предлагаемой ремонтной технологии.

а

b

Рис. 22. Расчетно-экспериментальное обоснование ремонтной технологии диска паровой турбины ( a , b )

Fig. 22. Computational-experimental substantiation of repair technology of steam turbine disk ( a , b )

Определение остаточной долговечности лопатки диска паровой турбины ГТД с учетом истории нагружения

Следущий пример относится к приложениям имитационного моделирования в оценках долговечности лопаток паровых турбин. Одной из актуальных задач эксплуатации является защита передних кромок лопаток, воспринимающих воздействие паровоздушной смеси с взешенными частицами включений абразивного и коррозионного происхождения. Нанесение защитных покрытий осуществляется путем накладок, электролегирования, имплантации элементов за счет газопламенного напыления. В ряде случаев подобные технологии приводят к появлению подповерхностных дефектов, недоступных для визуального контроля, как это показано на рис. 23, а .

Для оценки характеристик долговечности лопаток паровых турбин были реализованы две технологии испытаний на основе имитационного моделирования. Первая из них состояла в испытаниях натурных лопаток габаритами 759 мм по высоте (рис. 23, b, c). Для эксплуатационных условий нагружения лопатки в составе диска на основе расчетов МКЭ были установлены центробежные нагрузки и погонные углы геометрической и аэродинамической закрутки профиля пера лопатки при максимальных числах оборотов турбины. Для модели- рования этих условий в эксперименте была разработана специальная оснастка передачи крутящего момента и осевой силы на натурную лопатку с использованием электрогидравлического стенда (рис. 23, d). Программа испытаний носила сопоставительный характер для гармонического, блочного и случайного спектров нагружения (рис. 24). В экспериментах фиксировался начальный крутящий момент и угол закрутки пера лопатки и далее прикладывалась по задаваемому профилю циклическая осевая нагрузка, эквивалентная центробежным силам. Состав случайного спектра нагружения лопатки был сформирован по данным 198 000 изменений отбора мощности на одной паровой турбине в течение годового периода эксплуатации.

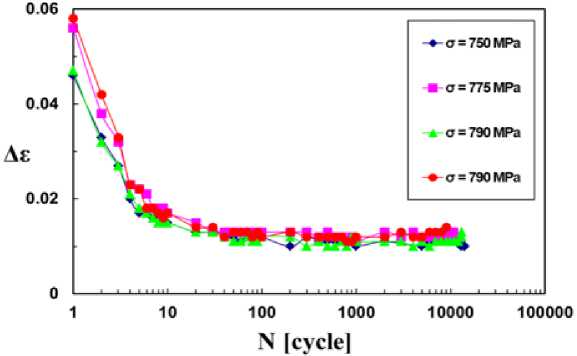
Одновременно с этим для повышения статистической достоверности характеристик долговечности была реализована вторая технология имитационного моделирования, согласно которой из пера лопатки вдоль передней кромки вырезались образцы-свидетели, испытанные по тем же трем профилям нагружения, что и натурные лопатки. Результаты этих испытаний приведены на рис. 25. Установлено, что для диапазона амплитуд напряжений, соответствующего эксплуатационному случайному спектру нагружения (рис. 24, с ), предельный размах амплитуд упругопластических деформаций стабилизируется после первого десятка циклов нагружения (рис. 25, а ).

a                   b c                      d

Рис. 23. Пора ( а ) на передней кромке лопатки ( b , c ) и установка для испытаний ( d ) при совместном растяжении с кручением

Fig. 23. Void ( a ) on the leading edge of the blade ( b , c ) and the test setup ( d ) under interaction tension and torsion

а                                   b                                    с

Рис. 24. Гармонический ( а ), блочный ( b ) и случайный ( с ) спектры нагружения лопатки

Fig. 24. Harmonic ( a ), block ( b ) and random ( c ) profiles of a blade loading

b

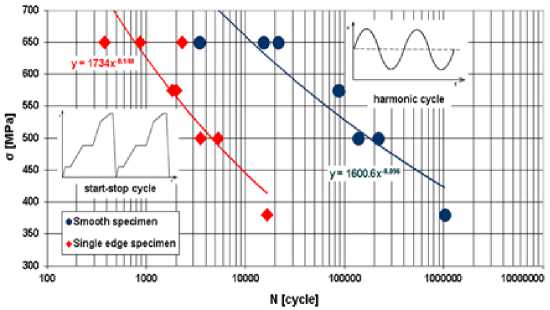
Рис. 25. Кривые усталости в деформациях ( а ) и напряжениях ( b ) для различных профилей нагружения

Fig. 25. Fatigue curves in terms of strains ( a ) and stresses ( b ) for different loading profiles

Сравнительный анализ спектров циклического нагружения (рис. 25, b ) показал, что минимальная долговечность соответствует блочному профилю пусков– остановов турбины из холодного состояния, по сравнению с гармоническим и случайным спектрами деформирования. Полученные результаты подтвердили целесообразность и эффективность реализации подходов имитационного моделирования в порядке осуществления регламентных и ремонтных работ паровых турбин.

Заключение

На примере лопаток и вращающиеся дисков паровых турбин и авиационных двигателей продемонстрирована методология имитационного моделирования с