Имитационный подход к решению задач распространения примесей

Автор: Губарев С.В., Берг Д.Б., Сергеев А.П.

Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc

Рубрика: Общие вопросы экологии промышленная экология

Статья в выпуске: 1-8 т.12, 2010 года.

Бесплатный доступ

В статье анализируется имитационный подход к моделированию распространения загрязнений от точечного источника заданной мощности. Приводятся математические описания созданных правил клеточного автомата. Показан пример расчета поля поверхностного загрязнения, полученного в результате имитационного моделирования. Результат моделирования сравнивается с расчетом по методике ОНД-86. Приведен пример реального профиля загрязнения, полученный в ходе планового проботбора снега вблизи каменного карьера.

Математическое моделирование, клеточные автоматы, имитационное моделирование

Короткий адрес: https://sciup.org/148199235

IDR: 148199235

Текст научной статьи Имитационный подход к решению задач распространения примесей

Невозможно представить себе техническое развитие любой страны, без привлечения внимания к экологическому аспекту такого развития. Любые глобальные или локальные воздействия на окружающую среду в той или иной степени вызывают отклик локальной экосистемы и биосферы в целом. Отсутствие до настоящего времени объективных методов оценики негативных экологических последствий породило прагматический стиль решения хозяйственных вопросов. В связи с этим основанная задача промышленной экологии заключается в оценке воздействий антропогенной деятельностью человека на окружающую его экосистему, а также выработке основных концепций, на основе существующих теоретических достижений, описывающих жизненные циклы экологических систем. Одним из важных этапов достижения такой цели является понимание сути природных процессов, возможность их моделирования и создания теоретических моделей, способных давать оценочные результаты степени техногенных загрязнений.

Процесс рассеивания загрязняющих веществ зависит от условий их эмиссии, переноса и турбулентного смешивания. За явление переноса отвечают процессы ветрового массопереноса, седиментации и вторичного массопереноса. Характер эмиссии загрязнения определяется параметрами источника. Существует множество моделей для анализа распределения концентрации загрязняющего вещества от различного рода источников загрязнений и атмосферных параметров. Одной из распространенных моделей являются Гауссовы модели [1], предназначенные для

моделирования распространения загрязнения без учета рельефа местности, которые модифицируются путем введения эмпирических коэффициентов, учитывающих возможное повышение концентрации в застой-ных зонах вблизи зданий, сооружений, впадин и лощин и т.п. Такой подход использован, например, в документе ОНД-86. Этот метод рекомендуется для установления нормативов ПДК (предельно допустимых концентраций) в Российской Федерации. Данная методика предназначена для расчета приземных концентраций в двухметровом слое над поверхностью земли, а также вертикального распределения концентраций. Степень опасности загрязнения атмосферного воздуха характеризуется наибольшим рассчитанным значением концентрации, соответствующим неблагоприятным метеорологическим условиям, в том числе опасной скорости ветра. В данной работе рассматривается 2 подхода к моделированию рассеивания загрязняющих примесей в атмосфере. Первый подход реализован на общепринятой в Российской Федерации методике ОНД-86, в качестве второго подхода используется имита-ционное моделирование на основе клеточного автомата.

Имитационное моделирование на основе метода клеточных автоматов. Имитационные модели в вычислительной среде клеточных автоматов (КА) [2, 3, 6] являются альтернативой дифференциальным уравнениям при моделировании сложных физических процессов. Модели КА хорошо зарекомендовали себя в различных физических приложениях и позволяют относительно легко реализовать суперпозицию источников загрязнения различной формы и интенсивности, а также мультипликативное влияние нестационарности выбросов и стохастичности метеорологических процессов. Основные принципы построения имитационной модели представлены в работах [2-4, 6], здесь же представлены созданные элементы модели КА.

Модель распространения загрязнений. Основными элементами модели КА являются пространства, правила и окрестности правил. Для имитационного моделирования перераспре деления загрязнения были созданы пространства, представленные в табл. 1 и правила, представленные в табл. 2.

Таблица 1. Пространства имитационной модели

Описание	Аналог аналитического выражения
Пространство концентраций
Кортеж M ( r , t ) = ^п ( r )^ описывает распределение концентрации в каждой точки пространства, в каждый момент времени	Начальные условия вида: С ( X , У , z ,0) = f c ( X , y , z ) концентрация загрязняющего вещества в начальный момент времени
Пространство поверхности
Кортеж Srf ( r , t ) = PROWSE ( r ), H_src ( r ), Z_srf ( r )} описывает подстилающую поверхность. POW_src ( r ) Мощность источника H src ( r ) Высота источника Z srf ( r ) Уровень шероховатости	Граничные условия вида: h ( x , y ) = f ( x , y ) уравнение описывает распределение высоты поверхности. Здесь же определяется функция мощности действующих источников f s ( X , y , z , t ) .
Пространство ветра
Кортеж W ⁽ ^r , t ) = u Wind d ⁽ ^r ^ Описывает направление и скорость ветра к каждой точке пространства	u ⁽ ^x , y , ^z , Ф ) = f U ⁽ ^x , y , ^z , ф ) функция распределения скорости и направления ветра

Таблица 2. Правила имитационной модели

Описание правила КА Аналитическое выражение

Ветровой массоперенос

P [ M ( r + r_c , t ) = m 1 и M ( r c , t ) = m ₂ и m ₂ > 0 о

_ _— _ ⁽ ^r ^- ^r 0 ⁾² _

M ( r + r c , t + 1) = m 1 + m ₂ и M ( r c , t + 1) = 0] ~ e ° ² , V r э N ( r ₀)

^r o среднее расстояние, которое пройдет частица за время одной итерации, под действием ветра. r расстояние до точки окрестности N ( r c ) N ⁽ r o) заданная окрестность правила. Наглядная демонстрация правила показано на рис. 2.

Перераспределение загрязнения вдоль направления средней скоро- а c a c

сти ветра — = и —, где U средняя d t d x

скорость ветра

Турбулентная диффузия

P [ M ( r + r_c , t ) = m 1 и M ( r_c , t ) = m ₂ и m ₂ > 0 о

M ( r + r_c , t + 1) = m 1 + m ₂ и M ( r_c , t + 1) = 0] = P td , V r э N ( r ₀)

^P td вероятность турбулентной диффузии. В зависимости от заданной окрестности можно установить отдельно степень турбулентности по каждому направлению

Выражение описывает перераспределение концентрации в атмосфере за счет турбулентной диф- . a C д „ д C

фузии — = ^ K i —, где K i значе- ^д t i ^xi S v i

ние коэффициентов турбулентной диффузии по каждому направлению

Седиментация

P [ M ( r + r_c , t ) = m ₂ и M ( r_c , t ) = m 1 и m 1 > 0 о

, . r ± Vt - — —

M ( r + r c , t + 1) = m 1 + m ₂ и M ( r c , t + 1) = 0] = —L z ²", V r э { a 1 , a ₂}

L = | a 1 + a ₂ |

Знак ± ставится соответственно для a ■ , a ₂ Конкурирующие клетки .

J a , < v z t i < a 2 выводятся из соотношения I

^ a 2 = a j + h c .

v _z средняя скорость седементации частиц (м/с), t i время одной итерации (с),

Выражение описывает перераспределение концентрации загрязнения за счет процесса оседания частиц на поверхность д C д C

_Sty -^-юуу , где ю средняя скорость

оседания частиц

Эмиссия загрязняющих веществ

P [ M ( r + r_c , t ) = m 1 и Srf ( r_c , t ) э S о

M ( r + r_c , t + 1) = m 1 + Pow ] = P_src , V r э N ( r_c )

Выражение описывает влияние на концентрацию загрязнения за счет действия источников

P _src вероятность эмиссии источника. Правило описывает эмиссию загрязняющих веществ от источников загрязнения. Мощность источника и вероятность выброса задаются отдельно для каждого источника. Геометрическая форма источника задается окрестностью правила эмиссии, рис. 3.

д C г

= f s ( x , У , z , t )

^д t , где функция

^fS ⁽ ^x ^, ^y ^, ^z ^, ^t ⁾ описывает мощность источников загрязнений

Сравнение результатов имитационной модели и методики ОНД-86. Моделировалось распределение загрязнений от точечного источника заданной мощности. В качестве результата моделирования выступает поле концентраций загрязняющего вещества. Методика

ОНД-86 была реализована в вычислительной среде MathCad, ее реализация основана на документе [5]. Основные параметры моделей представлены в табл. 3, результаты моделирования – на рис. 1.

Таблица 3. Параметры имитационной модели и методики ОНД-86

Параметр	Имитационная модель	Методика ОНД-86
скорость седиментации v z	0,1 м/с	F=1
скорость ветра u , м/с	0/5	U=0,5
направление ветра α u	0 º	всегда вдоль оси oX
кол-во источников	1	1
мощность источника	0,5 г/c	M=0,5 г/с
тип источника	точечный	точечный
высота источника	10 м	H=10 м
коор-ты источника, м	(20,60)	(20,60)
размерность матрицы, клетки	500x120x20	-
размер одной клетки, м	1	-
время одной итерации, с	1	-
количество итераций	1200	-
перегрев струи dT	-	0,001 ≈ 0 (отсутствует)
параметр атмосферы A	-	200
параметр η	-	1

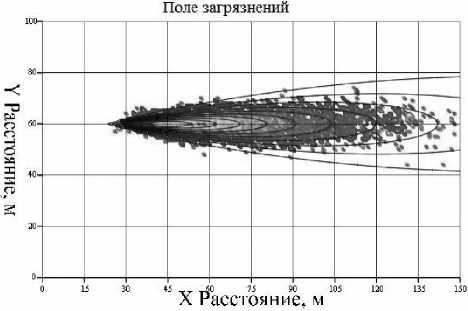
Рис. 1. Карта равных концентраций моделируемого поля поверхностных загрязнений. Градиентом серого – результат имитационного моделирования. Линиями – результат расчета по методике ОНД-86.

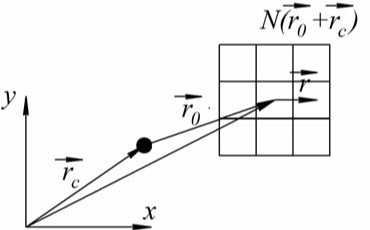
Рис. 2. Показана произвольная окрестность N ( r c ) точки r c . Окрестность задает геометрию источника загрязнения (загрязняющее вещество может появиться в любой клетке заданной окрестности)

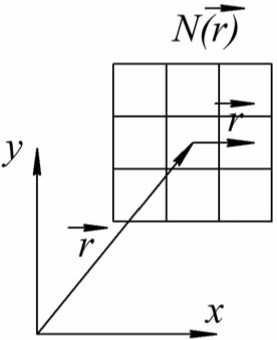
Рис. 3. Показано возможное перемещение частицы из точки r c в точку окрестности N ( r c + r o ). Окрестность определяет степень устойчивости выбранного направления движения

Выводы: в статье приведены 2 подхода к моделированию распространения загрязнений. Имитационный подход основанный на вероятностной природе правил КА, а также дискретности времени и пространства, показывает неравномерное поведение распределения вещества вдоль оси факела источника загрязнений, в то время как методика ОНД-86 предсказывает гладкое поведение распределения загрязняющего вещества. При усреднении нескольких реализаций имитационного моделирования, наблюдается сглаживание кривой распределения, и в среднем результаты двух подходов качественно совпадают. В работе [8] был проведен натурный эксперимент по выявлению массы пыли в снежном покрове в непосредственной близости от каменного карьера. В результате была построена кривая распределения массы пыли вдоль выделенного направления (вкладыш на рис. 6). В распределении присутствует явно выраженная стохастическая природа процессов перераспределения веществ, как и при имитационном моделировании.

В качестве отличительной особенности имитационной модели можно отметить возможность учета сложных граничных условий, а также простой учет физико-химических процессов в атмосфере (коагуляция частиц, нуклеация и т.п.) процессов вторичного перераспределеия вещества (вымывание, радиоактивный распад, почвенная диффузия и др.). Построенная имитационная модель является трехмерной, в то время как методика ОНД-86 оперирует двумерным полем распределения загрязняющего вещества. Дальнейшие направления в работе над имитационной моделью: учет сложной формы подстилающей поверхности, учет температурной стратификации атмосферы.

Список литературы Имитационный подход к решению задач распространения примесей

Бызова, Н.Л. Экспериментальные исследования атмосферной диффузии и расчеты рассеяния примеси/Н.Л. Бызова, У.К. Гаргер, В.Н. Иванов. -Л.: Гидрометеоиздат, 1991. 290 с.
Губарев, С.В. Имитационное моделирование распределения двухфазных загрязнений атмосферы/С.В. Губарев, К.А. Беклемишев, Д.Б. Берг//Материалы Международной молодежной научной конференции. Ереван. 2007. С. 22-27.
Wolfram, Stephen. A New Kind of Science//Wolfram Media, Inc., May 14, 2002. ISBN 1-57955-008-8
Методика расчета концентраций в атмосферном воздухе вредных веществ, содержащихся в выбросах предприятий. ОНД-86.
Тоффоли, Т. Машины клеточных автоматов/Т. Тоффоли, Н.М. Марголус. -М.: Мир, 1991. 280 с.
Чуканов, В.Н. Диагностика загрязнений снегового покрова растворимыми и нерастворимыми формами металлов/В.Н. Чуканов, А.П. Сергеев, С.М. Овчинников, А.Н. Медведев//Дефектоскопия. 2006. №9.
Сергеев, А.П. Горизонтальное распределение накопленной в снеге пыли от действующих карьеров на примере трех малых площадок и линейного профиля/А.П. Сергеев, В.Н. Чуканов//В сб. Урал. Радиация. Реабилитация. Екатеринбург: УрО РАН, 2004.

Статья научная