Impedance and dielectric properties of Bi2Sn2-xFexO7 stannates

Aerospace industry requires microelectronic materials that can operate over a wide temperature range. Promising materials are multiferroics, on the basis of which information can be recorded by magnetic and electric fields. One of such materials is bismuth pyrostannate. Bismuth pyrostannate Bi 2 Sn 2 O 7 belongs to the family of compounds with the pyrochlore structure [ 1 ] exhibiting the properties of ferroelectrics [2] and colossal magnetoresistance [3].

In the polymorphic Bi 2 Sn 2 O 7 , three structural modifications related to the pyrochlore structure were found. Above 900 K, the compound has a cubic structure with small displacements of Bi³⁺ ions from the ideal structure of pyrochlore and belongs to the y -phase [ 1 ] . In the temperature range of 390-900 K, в-phase with an orthorhombic structure is realized [ 4 ] . At room temperature, Bi 2 Sn 2 O 7 is in a non-centrosymmetric monoclinic structure (α-phase) with the space group P1c1 [5]. The structure of Bi 2 Sn 2 O 7 is well described by two interpenetrating oxide sublattices. The Sn 2 O 6 sublattice consists of Sn 2 O 6 octahedra connected at their vertices to form hexahedral rings. In the Bi 2 O′ sublattice, the Bi³⁺ cation is tetrahedrally coordinated by O' anions with linear O'–A–O' bonds.

It has been found that the transitions to the α- and β-phases occur with the rotation of the Bi 2 O′ tet-rahedra, which displace the Bi ions to the vertex of the α-phase and the edge in the β-phase of the SnO 6 oxygen octahedron. Correlated displacements of Bi³⁺ can lead to phase transitions into complex ordered structures, which in turn will lead to a change in macroscopic properties.

Displacement-type phase transitions were observed in a perovskite-type crystal structure (ABX3). The transition below Т с is accompanied by the appearance of ordered distortions of the crystal lattice, leading to a decrease in its symmetry. Depending on the nature of the elements that make up these compounds, ordered distortions can be associated with the rotation of the ВХ 6 octahedra relative to the coordinate axes or with the displacement of cations, or with both.

In KNbO s compounds, displacement-type processes are predominant at low temperatures [ 6 ] . In KNbO 3 single crystals, the phase transition is induced by the electric field with E = 50 kV/cm directed along the axis [101] of the orthorhombic cell of the antiferroelectric phase. Under the action of the field, the oxygen anions are displaced in opposite directions and the oxygen octahedra rotate [ 7 ] . The influence of structural transitions and the change in the distribution of defects due to the migration of Na ions was reflected in the electrical conductivity of KNbO s [ 8 ] . The temperatures of electrical conductivity and permittivity anomalies below 120 K are close to the temperatures of structural phase transitions and are caused by the domain dynamics that occurs in the vicinity of the phase transition [ 9 ] .

Double oxides with the pyrochlore structure exhibit a number of low-temperature magnetic and electrical phase transitions. For example, transitions to the spin glass state in Y 2 Mo 2 O 7 and spin liquid in Tb 2 Ti 2 O 7 , disordered spin ice in Ho 2 Ti 2 O 7 and Dy 2 Ti 2 O 7 , ordered spin ice in Tb 2 Ti 2 O 7 , superconductivity in Cd 2 Re 2 O 7 [10]. These physical properties of materials, which manifest themselves at extremely low temperatures, are one of the current trends in condensed matter physics.

In bismuth-containing complex oxides, for example, in undoped Bi13Mo5O34±δ and substituted ones, the transition from triclinic to monoclinic modification is observed with increasing temperature. In the Bi13Mo4.9Fe0.1O34±δ sample, as the temperature increases, the molybdenum-oxygen polyhedra are disordered. Such rearrangements in the oxygen sublattice can lead to the deviation of the structure parameters from the linear dependences at high temperatures, as well as to a change in the physicochemical properties, which was observed for all compositions of the considered solid solutions. In the presence of phase transitions from the monoclinic to the triclinic modification, the change in the slope of the dependences is fixed on the conductivity polytherms. The low-temperature range in polytherms is characterized by the highest values of activation energy Eact = 0,9 – 1,3 eV. The simultaneous analysis of the results of impedance and structural studies shows that the change in the conductivity of materials in the high-temperature and medium-temperature ranges correlates with the changes in the oxygen sublattice of oxides in the framework of the monoclinic modification. This is due to the disordering effect of the oxygen polyhedra. The dependence of the electrical conductivity on the dopant concentration has a parabolic form with a maximum. At this concentration, the structure is characterized by the greatest distortions and is substantially disordered. The best in terms of conductive characteristics is Bi13Mo4.7Fe0.3O34±g [11].

Cation doping changes the structure of pyrochlore and the basic physical properties of the compounds, since the structural and physical properties correlate with each other. This group of compounds can be potentially in demand as materials for electrochemical devices, electronic devices of a new generation due to the relatively low temperatures of the synthesis of doped bismuth titanates and a significant increase in their thermal stability. The possibility of distributing atoms of doping elements over two equivalent crystallographic positions increases the variability of the properties of compounds due to the different nature of the doping element, affects the defectiveness of the cationic and anionic sublattices, and transport properties of ions (in particular, mobile oxygen O').

Doping of bismuth titanate Bi 2 Ti 2 O 7 [ 12 ] with iron atoms leads to the decrease in the value of E g from 2.83 eV for Bi 2 Ti 2 O 7 to 2.43 eV (Bi 2 Ti 2 O 7 with the addition of 1% Fe). The decrease in the band gap energy is explained by the fact that iron atoms can be distributed in A and B positions. Due to their distribution in titanium positions, the mobility of holes and electrons decreases. In Bi 2 Ti 2–x M x O 7 compounds substituted by d-elements (where М = V, Cr, Mn, Fe, Ni,) with x = 0.5, the impurity level appears in the bandgap when the atoms of 3D-elements are distributed in positions of titanium in the band gap. When titanium is replaced by iron, the level is closer to the top of the valence band; when chromium is substituted, it is closer to the bottom of the conduction band. Bismuth iron-containing titanates Bi 1,6 Fe x Ti 2 O 7–δ (х ≤ 0,4) exhibit mostly electronic conductivity.

The heterovalent substitution of Bi³⁺ and Sn⁴⁺ ions in Bi 2 Sn 2 O 7 leads to the change in the temperature of the α→β transition [1; 13–16] and it can lead to a further decrease in the crystal symmetry. Substitution of Sn⁴⁺ ions by Fe³⁺ ions induces distortions of the crystal structure and with increasing concentration leads to the phase transitions of the displacement type. Thus, in Bi 2 (Sn 1-х Fe х ) 2 O 7 from concentrations x = 0.2 at T = 140 K, the transition from monoclinic to triclinic symmetry was found [17].

The absence of an inversion center in bismuth pyrostannate is a prerequisite for the existence of a ferroelectric order at low temperatures. The theoretical calculations carried out from first principles confirm this assumption [1]. In Bi 2 (Sn 0,8 Fe0,2) 2 O 7 magnetoelectric (ME) interaction up to 300 K was found [ 18]. The external electric field leads to the deformation of the crystal lattice and formation of electric polarization. The electric polarization induced by the magnetic field is an even function of the magnetic field, except for the area of the structural phase transition 140–160 K, where the linear magnetoelectric effect dominates. The electric polarization induced by the magnetic field decreases with heating.

The aim of the work is to determine the temperature interval for the formation of migratory electron polarization, which will manifest itself in the dielectric properties, and to establish the inductive contribution of electrons to the reactance associated with the space charge in the Bi 2 (Sn 1–х Fe х ) 2 O 7 sample, x = 0; 0.1; 0.2.

Experimental technique

The synthesis of Bi 2 Sn 2-х Fe х O 7 , х = 0,1; 0,2 was carried out by the method of solid-phase reaction. The synthesized samples correspond to the Pc monoclinic cell in the а-phase of Bi 2 Sn 2 O 7 [ 18 ] .

The electrical properties were studied by the four-probe method on a 6517 V electrometer in the temperature range 100–600 K. The impedance, capacitance, and loss tangent were measured on the AM-3028 component analyzer in the frequency range 1–300 kHz and the temperature range 100–600 K.

• 1.    Dielectric permittivity

The spectral and temperature dependences of the dielectric constants can be used to detect the electric dipole moment and determine its characteristics, even in the context of the local dipole moment in small clusters without long-range dipole order. The dielectric characteristics also reflect information about charge transport and charge ordering processes [19–23].

The temperature dependence of the dielectric permittivity of Bi 2 (Sn 1–x Fe x ) 2 O 7 , х = 0.1 and 0.2 is shown in Fig. 1. The real part of the dielectric permittivity for x = 0.1 (Fig. 1, a) has two Re(ε) maxima at temperatures of ~270–280 and ~640 K. The first maximum is associated with electron localization at T = 280 K and the second one is at T = 640 K with structural transition with the loss of the center of inversion. The change in dielectric permittivity (ε(Т = 280 K) – ε(Т == 100 K)) / ε(T = 100 K) at 280 K increases with decreasing frequency and reaches 3% at 1 kHz.

82 b

ф 76

О'

200      300      400      500      600

T, K

Рис. 1. Температурная зависимость реальной части диэлектрической проницаемости Bi 2 (Sn 1–x Fe x ) 2 O 7 : а – х = 0,1; кривая 1 соответствует 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz;

• 6    – 300 kHz; б – х = 0,2; кривая 1 соответствует 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz;

6 – 300 kHz. Пунктирные линии соответствуют теоретическим расчетам в модели Дебая (1.1)

Fig. 1. Temperature dependence of the real part of the dielectric permittivity Bi 2 (Sn 1–x Fe x ) 2 O 7 :

а – х = 0.1; curve 1 corresponds to 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz;

• 6    – 300 kHz; b – х = 0.2, curve 1 corresponds to 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz;

6 – 300 kHz. Dashed lines correspond to the theoretical calculations in the Debye model (1.1)

The temperature dependences of the imaginary part of the permittivity Im(T) for x = 0.1 (Fig. 2, a) also have an anomaly in the form of the wide maxima of dielectric losses in this temperature range. Let us describe the dielectric susceptibility in the Debye model:

Re(ε) = ε 0 + A / (1 + (ωτ 1 )²) + B / (1 + (ωτ 2 )²),                        (1.1)

Im(ε ) = Aωτ 1 / (1 + (ωτ 1 )²) + Bωτ 2 / (1 + (ωτ 2 )²),                       (1.2)

where τ 1,2 = τ 01,2 exp(–ΔE 1,2 / kT) – relaxation time; ΔE – activation energy. The adjustment to experimental data gives two energies ΔE1 = 1700 K and ΔE2 = 6400 K.

With the increase in the concentration of iron ions to x = 0.2, the shape of the dielectric permittivity curves changes. The temperature dependence of the real part of the dielectric permittivity (Fig. 2b) has a maximum at T = 140 K, which confirms the presence of the structural transition to triclinic symmetry [17]. Structural phase α→β transition for x = 0.2 is shifted towards lower temperatures up to T = 350 K. The dielectric losses in Bi 2 (Sn 1-x Fe x ) 2 O 7 at x = 0.2 (Fig. 2, b) are maximum in this temperature range, the intensity of which decreases with increasing frequency. These experimental results are consistent with softening of the IR modes, anomalies in the curves of the temperature dependences of the coefficients of thermal expansion and sound attenuation [17]. In the β phase, the transition occurs with the loss of the inversion center at 640 K, which also manifests itself in the abnormal increase in the dielectric permittivity and is described in the Debye model.

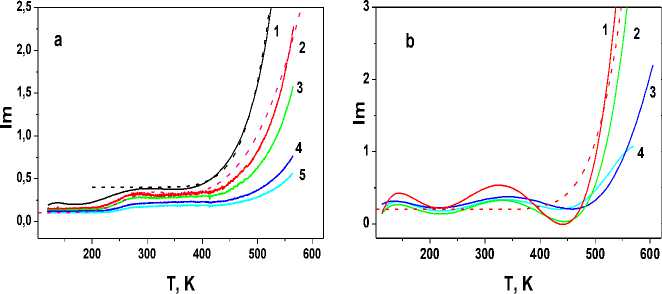
Рис. 2. Температурная зависимость мнимой части диэлектрической проницаемости Bi 2 (Sn 1–x Fe x ) 2 O 7 : а – х = 0,1; кривая 1 соответствует 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz;

б – х = 0,2; кривая 1 соответствует 5 kHz; 2 – 10 kHz; 3 – 50 kHz; 4 – 100 kHz.

Пунктирные линии соответствуют теоретическим расчетам в модели Дебая (1.2)

Fig. 2. Temperature dependence of the imaginary part of Bi 2 (Sn 1–x Fe x ) 2 O 7 dielectric constant: а – х = 0,1, curve 1 corresponds to 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz; b – х = 0.2; curve 1 corresponds to 5 kHz; 2 – 10 kHz; 3 – 50 kHz; 4 – 100 kHz.

Dashed lines correspond to the theoretical calculations in the Debye model (1.2)

At the frequency of 300 kHz, the imaginary part of the dielectric permittivity slightly depends on the temperature for x = 0.2. This is due to the electron migration polarization, which is dependent on grain boundaries in a polycrystalline sample. Electrons delocalize in a certain area (at the grain boundaries) and the electron localization radius and polarization increase with increasing temperature.

2.    Impedance

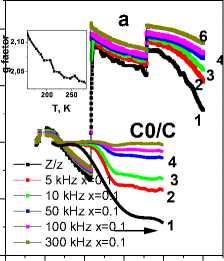
Impedance spectroscopy makes it possible to estimate the capacitive and inductive contributions of the current carriers in samples [24–26]. The impedance is calculated by the formula Z² = R² + X², where R is an active resistance; X is a reactance, which has capacitive Х С = 1 / wC and inductive X L = wL components. The temperature dependences of the normalized reactance of Bi 2 (Sn 1–x Fe x ) 2 O 7 , x = 0.1 and 0.2 are shown in Fig. 3. The jump temperatures of the imaginary part of the impedance Im(Z) / Im(Z(T = 80 K)) by 6–8% at 220 K for x = 0.1 and the change in the g-factor coincide (Fig. 3, a). At T = 215 K, the g-factor increased by 1% (inset, Fig. 3a) and the linewidth of the electron paramagnetic resonance sharply increases with decreasing temperature [18].

The difference in the temperature behavior of reactance X L,C from capacitive Х с (Fig. 3, a) indicates the inductive contribution, which provides information on the dynamic magnetic susceptibility χ(ω). Thus, the inductance (L) is proportional to the magnetic permeability (μ), L ~μ = 1 + χ and ∆ХL = χω(T) – χω(T = 80 K). For x = 0.1, the capacitive reactance is practically independent on temperature at high frequencies. When Х L and Х С are connected in series, the change in reactance ∆X L,C = Х L (Т) – Х С (Т) – Х L (Т = 80 К) – Х С (Т = 80 К) = Х L (Т) – Х L (Т = 80 К) = χ ω (T) – χ ω (T = 80 К) is caused by the increase in the dynamic magnetic susceptibility as a result of the appearance of electrons on the Fermi surface and the paramagnetic contribution. The Pauli susceptibility does not depend on temperature, which is in qualitative agreement with the experimental data. The jump in reactance at 360 K is caused by 1 % increase in the electron concentration at the Fermi surface.

1,04

1,02

1,00

0,98

0,96

0,8

1,0

0  100 200 300 400 500    0     200    400    600

T, K

T, K

Рис. 3. Температурная зависимость приведенного импеданса и приведенной емкости Bi 2 (Sn 1–x Fe x ) 2 O 7 : а – х = 0,1; кривая 1 соответствует 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz; 6 – 300 kHz.

На вставке приведена температурная зависимость g-фактора для х = 0,1; б – х = 0,2; кривая 1 соответствует 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz; 6 – 300 kHz

Fig. 3. Temperature dependence of reduced impedance and reduced capacity Bi 2 (Sn 1–x Fe x ) 2 O 7 : а – х = 0.1, curve 1 corresponds to 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz; 6 – 300 kHz; the insert shows the temperature dependence of the g-factor for x = 0.1; b – х = 0.2;

curve 1 corresponds to 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz; 6 – 300 kHz

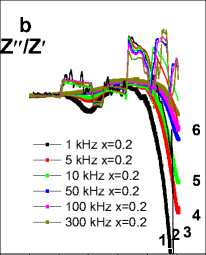
The temperature dependence of the impedance of Bi 2 (Sn 1-x Fe x ) 2 O 7 , x = 0,2 has an anomaly in the form of a Z"/Z ' (Т = 80 К) in the vicinity of Tm_m = 310 K, which decreases with the increase in frequency by 2 orders of magnitude. The temperature Т min practically does not depend on the frequency. The decrease in impedance in the range of 260–310 K occurs due to inductive reactance, since the capacitive reactance is practically independent of temperature in this interval. The localization of electrons in this temperature range leads to the decrease in the electron concentration on the Fermi surface and to the decrease in the contribution to the paramagnetic susceptibility X (L,C) = χ ω (T) – χ ω (T = 80 K) ~ –0,03. This is confirmed by the presence of a broad maximum in the temperature dependence of the active resistance (Fig. 4, b) at 260–340 K. Heating to 400 K again leads to the localization of charge carriers, the increase in capacitance, temperature independence of the resistance, and the decrease in the paramagnetic contribution of electrons to the magnetic susceptibility. Such an unusual temperature behavior of the impedance is associated with the presence of polymorphic transitions [27–28], the coexistence of crystalline domains with different phases, in which current carriers are localized [29–30].

When replacing tin ions with iron, the α → β transition stretches with respect to temperature. Thus, the temperature dependence of the sound attenuation coefficient of Bi 2 (Sn 1–x Fe x ) 2 O 7 , х = 0,2 has anomalies at T = 350 and 400 K, which are consistent with anomalies in the temperature dependence of the thermal expansion coefficient of the sample in the range 320–380 K. The domains containing iron ions begin to pass into the в-phase at T = 350 K [17 ] . Above 460 K, the decrease in impedance in Bi 2 (Sn 1–x Fe x ) 2 O 7 , х = 0.1 and 0.2, is caused by the increase in capacitance as a result of relaxation conduction.

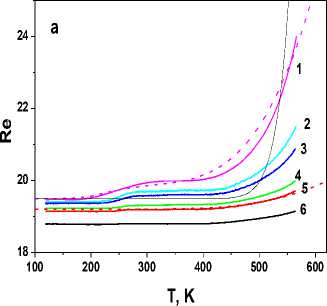
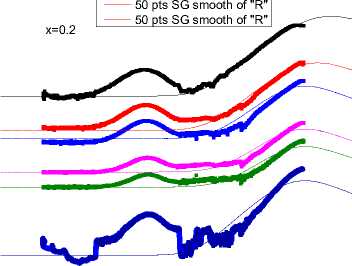
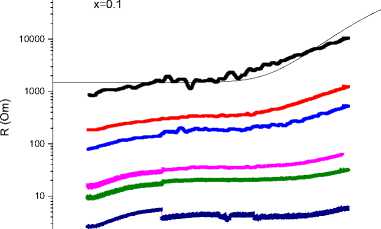
The temperature dependences of the resistance on alternating current of Bi 2 (Sn 1–x Fe x ) 2 O 7 , х = 0.1 and 0.2 are shown in fig. 4 for the range of frequencies from 1 to 300 kHz. The active resistance for x = 0.1 has small jumps at a temperature of T = 220 K and for x = 0.2 a wide maximum in the range of 260–360 K (Fig. 4, b). This anomalous portion of R(T) correlates with a broad maximum in the temperature dependence of the dielectric permittivity, which we attribute to the gradual transition of the compound to the β-phase. In the same temperature range, softening of the IR mode is observed at the frequency of 510–540 см^–1, which is responsible for stretching vibrations of the Bi-O' bond [17].

BiSnFeO x=0.1 1kHz

BiSnFeO x=0.1 5kHz

BiSnFeO x=0.1 10kHz

BiSnFeO x=0.1 50kHz

—■— 1 kHz x=0.2

—■— 5 Ohm x=0.2

—■— 10 kHz x=0.2

—■— 50 kHz x=0.2

—■— 100 kHz x=0.2

□■“ 300 kHz x=0.2

♦  BiSnFeO x=0.1 100kHz

—«— BiSnFeO x=0.1 300kHz

50 pts SG smooth of "R"

50 pts SG smooth of "R"

50 pts SG smooth of "R"

50 pts SG smooth of "R"

-■-- 50 pts SG smooth of "R"

1E7

"e              :

10000 к          :

10 0

200               400               600

T (K)

Рис. 4. Температурная зависимость сопротивления на переменном токе Bi 2 (Sn 1–x Fe x ) 2 O 7 : а – х = 0,1; кривая 1 соответствует 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz; 6 – 300 kHz; б – х = 0,2; кривая 1 соответствует 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz; 6 – 300 kHz. Сплошные линии соответствуют теоретическим расчетам (2.1)

50 pts SG smooth of "Smoothed Y3"

1       100         200          300         400         500

T (K)

Fig. 4. Temperature dependence of the resistance at alternating current Bi 2 (Sn 1–x Fe x ) 2 O 7 :

а – х = 0.1; curve 1 corresponds to 1 kHz; 2 – 5 kHz; 3 – 10 kHz; 4 – 50 kHz; 5 – 100 kHz;

6 – 300 kHz; b – x = 0.2; curve 1 corresponds to 1 kHz; 2 – 5 kHz; 3 – 10 kHz;

4 – 50 kHz; 5 – 100 kHz; 6 – 300 kHz. Solid lines correspond to theoretical calculations

At high temperatures, the AC resistance increases sharply for two concentrations. Active resistance characterizes the absorption of electromagnetic radiation, and it can be described in the Debye model:

Re(Z) = A ωτ / (1 + (ωτ)2),

(2.1)

where the relaxation time is described by the Arrhenius law τ = τ 0 exp(–ΔE / kT) with ΔE = 6400 K. The absorption maximum is reached in the the phase transition zone with the loss of the inversion centre, which is confirmed by the data of differential scanning calorimetry (DSC) obtained for Bi 2 (Sn 1– x Cr x ) 2 O 7 , х = 0 – 0.1. DSC detects smeared exo- and endoeffects in the region of 600 and 646 K [19]. The Debye model satisfactorily describes the temperature dependence of the resistance above 400 K. The maxima on the theoretical curves at T > 600 K are associated with the phase transition with the loss of the inversion centre; Т maх increases with increasing frequency [17].

Conclusion

In bismuth pyrostannate Bi 2 (Sn 1–x Fe x ) 2 O 7 , х = 0.1, the change in the g-factor at 220 K is associated with the inductive contribution of electrons to the impedance and the growth of the Pauli contribution to the paramagnetic susceptibility. The anomaly in the dielectric permittivity at 280 K is associated with the localization of current carriers. Above this temperature, the conductivity has an activation character. At approximately 360 K, an extended α→β transition with coexistence of phases was found, which is accompanied by an increase in the dynamic paramagnetic susceptibility. In Bi 2 (Sn 0,8 Fe 0,2 ) 2 O 7 , an inductive contribution to the impedance was found in the vicinities of the change in conduction type from tunneling to activation type and in the orthorhombic β-phase.