Импедансная спектроскопия (ВеО+TiO2)-керамики с добавкой наночастиц TiO2
Автор: Лепешев А.А., Павлов А.В., Дрокин Н.А.
Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu
Статья в выпуске: 3 т.12, 2019 года.
Бесплатный доступ
Настоящее исследование направлено на получение электропроводной двухкомпонентной керамики на основе ВеО с добавками микро- и нанокристаллического порошка TiO2. Керамика состава (BeO+TiO2) находит применение в радиоэлектронной технике в качестве эффективных поглотителей СВЧ-излучения и в других областях современной электроники. Природа возникновения электрической проводимости и поглощения СВЧ-поля в (ВеО+TiO2)керамике окончательно не установлена. Методом импедансной спектроскопии впервые исследованы электрические и диэлектрические характеристики данной керамики в диапазоне частот от 100 Hz до 100 МHz в зависимости от присутствия в составе керамики ВеО микро- и наноразмерной фазы TiO2. Установлено, что статическое сопротивление керамики с добавкой нанопорошка оксида титана существенно уменьшается по сравнению с сопротивлением исходной керамики с микропорошком TiO2. Показано, что действительная и мнимая компоненты диэлектрической проницаемости исследуемых керамик возрастают до аномально больших величин при понижении частоты действующего электрического поля, а в области высоких частот f ≥ 108 Hz начинается процесс диэлектрической релаксации, приводящий к росту тангенса угла диэлектрических потерь. Определены диэлектрические характеристики данных образцов керамик в условиях блокирования сквозной проводимости.
(вео+tio2)-керамика, микроструктура, электрофизические свойства, импеданс, частотная зависимость, диэлектическая проницаемость, тангенс угла диэлектрических потерь
Короткий адрес: https://sciup.org/146281201
IDR: 146281201 | УДК: 666.3:546.45-31.001.5 | DOI: 10.17516/1999-494X-0144
Текст научной статьи Импедансная спектроскопия (ВеО+TiO2)-керамики с добавкой наночастиц TiO2
чистой керамики BeO имеет величину ε = 6,9–7,2, а диэлектрические потери на частоте 1 MHz не превышают значения tg δ = 3 ⋅ 10-4.
При синтезе керамики, в состав которой добавляется диоксид титана TiO2, происходит изменение ее плотности в диапазоне 2,8–3,2 g/cm3 и уменьшение теплопроводности в диапазоне 150–65 W/(m ⋅ K) [4]. Если после спекания провести дополнительное прокаливание керамики в восстановительной атмосфере углекислого газа при 1650 К в течение 1,5-2 ч, то полученные образцы становятся электропроводными с удельной проводимостью в пределах от 8 ⋅ 10-8 до 4 ⋅ 10-1 (Ohm ⋅ сm)-1 [5]. Аналогичное возрастание проводимости происходит и при непосредственном спекании порошков BeO и TiO2 в вакууме в печах с графитовой футеровкой и графитовыми нагревателями в диапазоне температур 1723-1813 К [6]. Термообработка керамики в графитовой засыпке в атмосфере углекислого газа также приводит к возрастанию проводимости и способности поглощать СВЧ-излучение в гигагерцовом диапазоне частот [7, 8].
Оксид бериллия низкотемпературной модификации α-ВеО в обычных условиях кристаллизуется в структуре типа вюрцита, образованной плотной гексагональной упаковкой ионов кислорода с тетраэдрическими и октаэдрическими пустотами [9]. Ионы бериллия занимают половину тетраэдрических пустот и формируют гексагональную подрешетку. TiO 2 принадлежит к классу оксидов переходных металлов и имеет несколько модификаций, в данном случае рутил, который обладает тетрагональной кристаллической структурой. Валентная зона TiО 2 образована внешними р -электронами кислорода, а дно зоны проводимости – преимущественно возбужденными ионами титана [10]. Особое значение для электронных свойств диоксида титана, именно рутильной модификации, является наличие частично восстановленного титана (Ti3+), уровень которого расположен на ~ 0,2–0,8 эВ ниже дна зоны проводимости [11]. Эти ионы выступают в качестве доноров, приводя к электронному типу проводимости. Наличие Ti3+ определяет и проводимость получаемого оксида титана, удельное сопротивление которого уменьшается от величины 104–107 Ω·см до 102 Ω∙см [12].
При спекании ВеО+TiO 2 в печах с углеродными нагревателями или в восстановительной среде монооксида углерода, вероятно, происходит внедрение углерода во внутреннюю область керамики, который также может влиять на величину проводимости керамики. По результатам рентгеновской фотоэлектронной спектроскопии [13] установлено, что на границах между кристаллитами BeO в присутствии микро- или наночастиц TiO 2 могут возникать пока не установленные соединения, обладающие как проводящими, так и диэлектрическими свойствами.
Электрофизические свойства данных керамик практически еще не изучены. Вполне вероятно, что проводящие прослойки, возникающие на поверхности керамических кристаллитов, приводят к сложным траекториям движения носителей тока, которые могут зависеть от частоты и величины приложенного к образцу переменного электрического поля. Не исключено, что подвижные заряды могут накапливаться на границах отдельных кристаллитов и это может способствовать появлению внутренних неоднородных электрических полей, усложняющих процессы движения и релаксации носителей тока. Основной задачей настоящей работы является отработка технологии изготовления экспериментальных образцов керамики состава ВеО с добавками микро- и нанокристаллической фазы TiO 2 с целью изучения их влияния на процессы электропереноса и поляризацию данных керамик методом измерения электрического импеданса в диапазоне частот от 100 Hz до 100 МHz.
Особенности получения и введение наночастиц TiO2
В качестве исходного образца двухкомпонентной керамики использовался образец состава BeO+30 мас. % TiO2. Для изготовления такой керамики применяется обожженный порошок оксида бериллия со средним размером кристаллитов 5 мкм и микронный порошок диоксида титана ТУ 6-10-727-78 с таким же размером частиц. В микронный порошок добавляли 1 мас. % нанодисперсного порошка TiO2, полученного на плазмохимическом реакторе низкого давления, для синтеза наноматериалов, разработка кафедры ЮНЕСКО «Новые материалы и технологии» СФУ, г. Красноярск [14].
На рис. 1 а, б изображена типичная микрофотография наночастиц. Порошок представляет собой смесь агломерированных частиц неправильной формы размером от 5 до 10 нм. Встречаются образования размером до 15 нм, что, по-видимому, является агломератами более мелких частиц. Форма всех частиц, как правило, близка к сферической. Исследование гранулометрического состава показало, что полученный нанопорошок имеет логарифмически нормальный характер распределения со средним размером частиц – 10 нм. Отклонение от среднего размера составляет не более 30 %.
Методом дифракции электронов в выбранной области была получена информация о кристалличности наночастиц (рис. 1 б) . На дифракционной картине видны пятна, а также размытые кольца, которые указывают на характеристику кристалличности наноматериалов.
Получали образцы ВеО керамики c добавкой 30 мас. % порошка TiO2, имеющего микронные размеры, и керамики ВеО+20 мас. % TiO2 микронного размера, в который дополнительно вводили 1 мас. % нанопорошка TiO 2 .
Исходные компоненты шихты ВеО+TiO2 перемешивали в специально разработанном реакторе импеллерного типа, в дистиллированной воде в условиях непрерывного барботирования сжатым воздухом. Экспериментальная установка представляет собой цилиндрическую, вертикально расположенную емкость из нержавеющей стали на жестком основании, внутри которой установлен вал с лопастями, в процессе вращения которого происходит перемешивание шихты (рис. 2).
Электродвигатель 1 приводит во вращение вал с лопастями 3 , который осуществляет перемешивание компонентов шихты 4 с дистиллированной водой в соотношении 1:2. В про-

Рис. 1. Микрофотография полученных наночастиц TiO2 и выбранная область дифракции электронов
Fig. 1. Micrograph of the obtained TiO2 nanoparticles and the selected region of electron diffraction
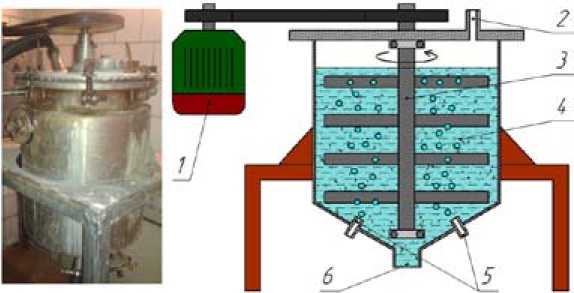
Рис. 2. Фотография и принципиальная схема работы реактора Р-60. 1 – электродвигатель; 2 – канал подачи сжатого воздуха; 3 – вал с лопастями; 4 – шихта; 5 – подача сжатого воздуха для барботирования шихты; 6 – сливное отверстие
Fig. 2. Photograph and schematic diagram of the operation of the reactor R-60. 1 – electric motor; 2 – compressed air supply channel; 3 – shaft with blades; 4 – charge; 5 – compressed air supply for bubbling the charge; 6 – drain hole цессе работы реактора для более эффективного перемешивания шихты в его объем непрерывно подается сжатый воздух 5 под давлением 0,2 – 0,5 кгс/см2.
Далее, были приготовлены шликерные массы на основе органической связки: воск, парафин, олеиновая кислота, из расчета потерь при прокаливании (ППП) 9,5 %. Воск-парафиновая связка закладывалась в соотношении (масс. %): парафин – 82 %; воск – 15 %; олеиновая кислота – 3 %. Работы по формованию заготовок проводили на установке длинномерного литья термопластичных шликеров. После операции выжига органической связки и спекания образцов в графитовой засыпке с использованием форвакуумной печи с углеродными нагревателями образцы шлифовали алмазным инструментом. Технология получения обоих типов образцов (ВеО+TiO2)-керамики с микронным порошком TiO2 и с добавлением нанопорошка диоксида титана одна.
Оптимальный температурный режим спекания подбирали по максимальному значению кажущейся плотности и размеру кристалла. Нагрев печи производили с шагом по 373 К в час в интервале температур 1753-1813 К, выдержка при максимальной температуре 1 ч, охлаждение до 1473 К под нагрузкой, далее естественное охлаждение. Изменение плотности полученных образцов в зависимости от температуры приведено на рис. 3.
С увеличением температуры спекания прямо пропорционально возрастает плотность образцов. При достижении температуры 1803 К наблюдается максимальная плотность (3,2 г/см3) у образцов с микропорошком TiO 2 . Дальнейшее увеличение температуры спекания этих образцов приводит к снижению их плотности. Это согласуется с данными работы [15], где показано, что введение в керамику ВеО микропорошка диоксида титана TiO 2 в количестве 5, 10, 20 и 30 мас. % в одинаковых термодинамических условиях в процессе спекания сопровождается ростом значений плотности от 2,8; 2,88; 2,99 и 3,2 г/см3 соответственно. В образцах с добавлением 1 мас. % нанопорошка TiO2 в состав BeO+20 мас. % микронного TiO2 максимальная плотность образцов не превышала значения 3,12 г/см3. Для достоверности полученного результата по – 370 –
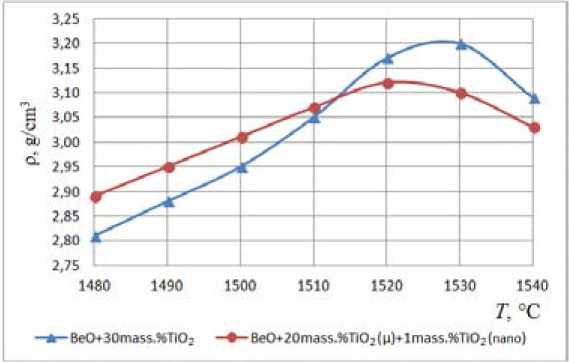
Рис. 3. Зависимость кажущейся плотности от температуры спекания образцов BeO+30 мас. % TiO2(мкм) и BeO+20 мас. % TiO 2 (мкм)+1 мас. % TiO 2 (нано)
Fig. 3. Dependence of apparent density on sintering temperature of BeO + 30 wt. % TiO2 (µm) and BeO + 20 wt. % TiO 2 (µm) + 1 wt. % TiO 2 (nano) samples
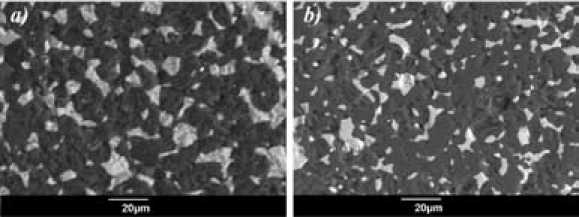
Рис. 4. Микроструктура исследуемых образцов. Светлые структурные элементы – TiO2, темные – ВеО:
а – ВеО + 30 мас. % TiO (мкм); b – BeO+20 мас. % TiO (мкм)+1 мас. % TiO (нано) 2 22
Fig. 4. Microstructure of the studied samples. Light structural elements – TiO2, dark – BeO: a – BeO + 30 wt. % TiO 2 (μm); b – BeO + 20 wt. % TiO 2 (µm) + 1 wt. % TiO 2 (nano)
определению закрытой плотности керамических образцов в зависимости от температуры спекания анализ плотности проводили на десяти различных образцах из одной и той же партии. Среднеквадратичное отклонение измеренных значений плотности не превышало 1 %. Микроструктуру экспериментальных образцов исследовали на растровом (сканирующем) электронном микроскопе с приставкой энергодисперсионного микроанализа JSM-6390LV. Результаты микроанализа представлены на рис. 4.
Исследования микроструктуры композиционной керамики состава ВеО+30 мас. % TiO2(мкм) показывают, что она представляет собой механическую смесь с достаточно крупными включениями TiO2 (рис. 4а). В структуре наблюдается неравномерное распределение микрокристаллов TiO2 с образованием достаточно крупных скоплений, до 30 мкм. При этом структурные элементы TiO2 стремятся к более округлой форме, также наблюдаются области сгруппированных кристаллов. В образцах керамики с добавкой наночастиц (рис. 4b) структурные элементы TiO2 имеют значительно меньшие размеры, не более 10 мкм, наблюдаются – 371 – тонкие и вытянутые фрагменты. По-видимому, нанопорошок заполняет пустоты между кристаллами ВеО, смачивая их и растекаясь по поверхности. Расплав ограничивает скорость рекристаллизации микрокристаллов ВеО.
Далее производили сравнение электрофизических свойств керамики (ВеО+30 мас. % TiO2), где диоксид титана имел микронные размеры и керамики BeO+20 мас. % TiO2 микронного размера с добавкой 1 мас. % нанопорошка TiO2.
Импедансная спектроскопия экспериментальных образцов
Измерения частотной зависимости импеданса полученных образцов керамики проводили на анализаторе спектров AgilentE 5061B в диапазоне частот от 10 Hz до 100 МHz. Сущность данного метода заключается в определении электрофизических характеристик композитных материалов в зависимости от частоты переменного напряжения, подаваемого на электроды, между которыми находится образец. Измерение модуля импеданса \Z\ основано на определении мгновенных значений переменного тока, текущего через образец. Одновременно фиксируется и сдвиг фазы между током и напряжением [16].
Для измерений импедансных характеристик полученных керамик на торцевые поверхности образцов диаметром 7,0-0 j и толщиной 1,0-0 j мм прикатывался тонкий ( ~ 0,2 мм) слой ’ ’ индия, который прижимался к поверхностям образца миниатюрной струбциной для обеспечения стабильного контакта на постоянном и переменном токе. С помощью игольчатых штырей подготовленная ячейка с керамикой подключалась к измерителю импеданса и проводилась регистрация на электронный носитель частотной зависимости импеданса |Z| и угла сдвига фазы (φ) между током и напряжением. Затем рассчитывались частотные зависимости действительной (Z' = |Z| Cosф) и мнимой (Z" = |Z| Sinф) компонент импеданса, которые позволяют определять основные комплексные электрофизические характеристики исследуемого материала.
На рис. 5 приведены результаты измерения частотной зависимости модуля импеданса \Z\(f) и угла сдвига фазы ф(/) между током и напряжением для двух подготовленных образ-
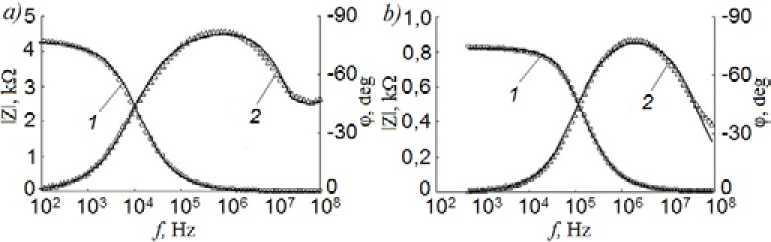
Рис. 5. Частотные зависимости модуля импеданса Z(1 ) и угла сдвига фазы ф ( 2 ) (белые маркеры) для двух образцов керамики: а - с микропорошком TiO2; b - у образцов с микронным порошком с добавкой 1 мас. % нанопорошка TiO2
Fig. 5. Frequency dependences of the impedance modulus Z (1) and phase angle угла (2) (white markers) for two ceramic samples: a - with TiO2 micropowder, b - for samples with micron powder with the addition of 1 wt. % TiO2 nanopowder цов керамики следующего состава: (образец а) BeO+30 мас. % TiO2 с размером зерна TiO2 и (образец b) состава BeO+20 мас. % TiO2(мкм)+1 мас. % TiO2 нанопорошка с размером зерна 30-50 нм.
Сплошные линии - результат аппроксимации импедансных спектров с помощью эквивалентных электрических схем (рис. 6). На графиках рис. 6 видно, что для образца ( а ) модуль импеданса в области низких частот f ~ 103 Hz имеет значение | Z | ~ 4,3 кО и с возрастанием частоты до f ~ 10 8 Hz монотонно уменьшается до значения 3,6 О. Фазочастотная характеристика керамики начинается почти с нуля, так как на низких частотах через образец протекает лишь действительная компонента тока, определяемая статическим сопротивлением материала. При увеличении частоты электрического поля появляется реактивная (емкостная) составляющая тока, поэтому фазовый угол увеличивается до значения ф = - 82° на частоте 106 Hz (рис. 5 а ). С дальнейшим ростом частоты вновь происходит уменьшение фазы до значений φ≈–47° на частоте 108 Hz.
Как следует из данных рис. 5 b , для керамики, содержащей наночастицы TiO2, низкочастотные значения модуля импеданса существенно уменьшились и составляют величину |Z| = 830 Ω. Фазовый угол на частотах f < 103 Hz практически равен нулю, однако на частотах f > 10 5 Hz характер поведения модуля импеданса | Z |( f ) и фазы ф ( / ) почти идентичен предыдущему образцу.
В методе импеданса для анализа резистивно-емкостных свойств исследуемых веществ и для понимания происходящих в них электрофизических процессов принято использовать метод построения подходящих электрических схем, импеданс которых согласуется с экспериментом. Различные радиотехнические элементы этих схем могут моделировать не только внутреннюю часть образца, но также поверхностные свойства и даже возникающий в некоторых случаях интерфейс вблизи электрических контактов. Для данных образцов керамики с помощью специальной программы EISA - analizer были подобраны наиболее подходящие эквивалентные схемы, показанные на рис. 6 a , b .
Результаты численной аппроксимации импедансных спектров с помощью этих эквивалентных схем обозначены на рис. 5 a , b сплошными линиями.
Как видим, обе схемы содержат обычные радиотехнические элементы R -сопротивление и С -емкость. В этих схемах присутствует линейно зависимый параметр, искусственный элемент постоянной фазы (СРЕ ), который в некоторой степени отражает электрические свойства самых
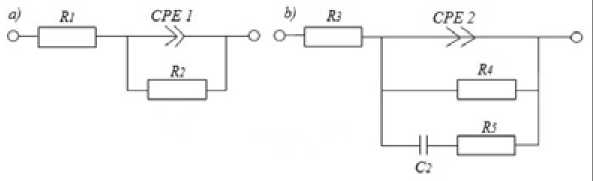
Рис. 6. Эквивалентные схемы для образцов: а - BeO+20 мас. % TiO2+1 мас. % нано TiO2; b - BeO+30 мас. %
TiO 2 (mkm)
Fig. 6. Equivalent schemes for samples: a - BeO + 20 wt. % TiO2 + 1 wt. % nano TiO2; b - BeO + 30 wt. % TiO2 (pm)
разных структурно неоднородных материалов. Импеданс ( ZCPE ) этого элемента записывается в следующем виде:
CPE A ( i ® ) n A ® n
( n) . . ( n)
cosl n— I- i sinl П— I
I 2) I 2)
где А - числовой множитель; О - круговая частота; i - мнимая единица; п - показатель степени, определяющий характер частотной зависимости импеданса (–1 ≤ η ≤ 1) [17]. Элемент CPE имеет как действительную, так и мнимую компоненту. Для целых значений η = 1, 0, –1 элемент CPE вырождается до обычных C- , R- , L- элементов. Дробные значения показателя степени п <1 формально характеризуют кластерную структуру материала.
Наиболее простая электрическая схема для керамики с нанопорошком TiO2 (рис. 5 a ), содержит всего три элемента: сопротивление R 1 = 2,9 О, R 2 = 827 О и элемент СРЕ 1 с числовым множителем А 0 = 5,3240-9 и показателем степени близким к единице п = 0,92. Меньшее количество сопротивлений в схеме для нанофазного образца, как будет показано далее, способствует увеличению удельной проводимости, тангенса угла диэлектрических потерь и диэлектрической проницаемости. Можно отметить, что сопротивление R 2 практически совпадает по величине с низкочастотным импедансом данной керамики | Z | = 830 Ω и естественно моделирует статическое сопротивление керамики. Сопротивление R 1 = 2,9 О в области радиочастот остается практически незамеченным, однако с ростом частоты, когда импеданс образца уменьшается, это сопротивление вносит ощутимый вклад в формирование импедансного спектра. В частности, именно это сопротивление в области высоких и, возможно, сверхвысоких частот приводит к наблюдаемому в спектре импеданса уменьшению фазы протекающего через образец переменного тока. Результаты численной аппроксимации экспериментально измеренного спектра импеданса данной керамики с помощью эквивалентной схемы обозначены на рис. 5 b сплошными линиями. Как видно совпадение расчета с экспериментом вполне удовлетворительное.
Для образца керамики с микропорошком TiO2, частотная зависимость импеданса приведена на рис. 5 а , а эквивалентная схема показана на рис. 6 b . Эта схема более сложная и помимо элемента СРЕ 2 содержит две параллельные цепи, одна из которых состоит из сопротивления R 4 = 4300 О, моделирующего статическое сопротивление керамики. Вторая цепь образована последовательно включенными элементами C 2 = 2,940-8 F и R 5 = 4 О, которые формируют импедансные характеристики в области средних частот. Элемент СРЕ 2 имеет числовой множитель А 0 = 2,940-8 и показатель степени n = 0,72. Этот показатель степени означает, что элемент СРЕ 2 можно трактовать как частотно-зависимую емкость и одновременно как частотно-зависимое сопротивление. Резистор R 3, как и для предыдущего образца, служит для моделирования высокочастотных электрических потерь. Для моделирования импеданса в дециметровом и сантиметровом диапазонах длин волн может потребоваться введение дополнительных элементов.
Кластерная структура этих проводящих керамик, несомненно, отражается и на таких электрофизических характеристиках материала, как удельная проводимость и диэлектрическая проницаемость. По экспериментально измеренным спектрам импеданса проводился расчет действительной и мнимой компонент удельной проводимости (σ’, σ”) и диэлектрической проницаемости (ε’, ε”) в соответствии со следующими формулами:
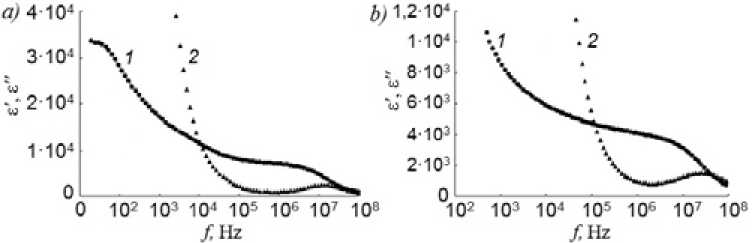
d Z"(to) d d - Z"Vto) d ст’(ю) = Y'(to) =——; s Z (®)2 s S Z (ю)2 S (2) £" (to ) = - Z’’(to)d ; £oAZ (to) 2S’ £""(to) = Z '(to )d £ to (to)2s ’ где Y’(ω) и Y”(ω) – действительная и мнимая компоненты адмиттанса керамики; d – толщина пластины исследуемой керамики; S – площадь контактов измерительной емкостной ячейки; ε0 – диэлектрическая проницаемость вакуума [18]. Частотные зависимости действительной и мнимой компонент проводимости приведены на рис. 7а, b. Как видим, на рис. 7 в области низких частот f≤ 10 – 105 Hz действительная компонента проводимости (1) этих образцов мало зависит от частоты и составляет величину 5,И0-3 Q-1^m-1 (образец a) и 2,700-2 Q-1^m-1 (образец b). Однако в интервале частот f ~ 104-108 Hz действительная компонента проводимости обоих образцов монотонно возрастает более чем на два порядка. Мнимая компонента проводимости (2) σ”(ω) обоих образцов керамик в логарифмических координатах возрастает с увеличением частоты почти линейно и определяется величиной их эффективной емкости σ”(ω) = ω⋅С. Однако при подходе к частоте f ~ 100 MHz имеется тенденция к отклонению от линейности в связи с появлением высокочастотной дисперсии диэлектрической проницаемости образцов и их емкости. Тангенс угла потерь (3) для образца с микронным порошком TiO2 (рис. 7а) минимален на частоте f ~ 1 MHz (а), где реактивная компонента проводимости кривая (2) преобладает над активной компонентой (1). Максимум тангенса угла потерь для этой керамики (3) выявляется при подходе к частоте f ~ 100 MHz и достигает значения – 1,0. На этой частоте активная компонента проводимости (1) становится сравнимой с реактивной компонентой (2), рис 7а. В образце с нанопорошком (рис. 7b) максимум угла потерь (3), вероятно, находится на частотах f > 100 MHz и на этой частоте имеет значение – 1 5. Для выяснения возможных причин возрастания активной компоненты проводимости с ростом частоты осуществлялась численная аппроксимация электрических спектров, приведенных на рис. 7а, b с помощью хорошо известного универсального соотношения: Рис. 7. Частотная зависимость действительной σ’ (1) и мнимой σ” (2) компонент удельной проводимости. На правой оси приведена частотная зависимость тангенса угла диэлектрических потерь (3), tgS. а - образец состава BeO+30 мас. % Т1О2(мкм); b - образец состава BeO+20 мас. % Т1О2(мкм)+1 мас. % Т1О2(нано) Fig. 7. Frequency dependence of real σ’ (1) and imaginary σ” (2) conductivity components. On the right axis shows the frequency dependence of the tangent of dielectric loss angle (3), tgδ. a – a sample of the composition BeO + 30 wt. % TiO2 (цт); b - sample of BeO + 20 wt. % TiO2 (pm) + 1 wt. % TiO2(nano) о'(ю) = gdc + a -to5, (4) где σdc – стационарное значение проводимости, a – численный коэффициент и s – показатель степени 0<5< 1 [19]. Для образца с микропорошком TiO2 (рис. 6b) был получен показатель степени 5 = 0,94, который близок к единице и указывает на проводимость, которая осуществляется перетеканием носителей тока от одного проводящего массива к другому. Однако формальное значение s < 1 может говорить о присутствии «прыжковой» проводимости, возникающей либо внутри кластеров, либо между ними. Такая проводимость возможна при наличии ионов титана с различной валентностью. Возможность существования обмена валентностью между гомологическими сериями оксидов TiО с участием вакансий по кислороду рассматривалась в работе [20]. При аппроксимации проводимости образца с нанопорошком TiO2 (рис. 6а) по формуле (4) показатель степени достигает величины 5 = 1,96, что полностью исключает прыжковую проводимость. Сквозная проводимость этой керамики, по-видимому, реализуется за счет перетекания или туннелирования носителей заряда между проводящими участками на поверхности наночастиц TiO2. В то же время могут возникать и отдельные проводящие островки, которые изолированы друг от друга. В этом случае на низкой частоте происходит смещение зарядов к границам этих островков, что сопровождается увеличением степени локальной поляризации и увеличением действительной компоненты диэлектрической проницаемости. С ростом частоты смещение зарядов начинает отставать от внешнего поля по фазе и возникает дополнительная релаксационная компонента тока, которая дает увеличение показателя степени в выражении (4) почти до s = 2 и приводит к возрастанию диэлектрических потерь. Частотные зависимости действительной и мнимой компонент диэлектрической проницаемости исследуемых образцов изображены на рис. 8а, b. Отметим, что наблюдаемые огромные значения компонент диэлектрической проницаемости в области низких частот часто возникают в самых различных структурно-неоднородных материалах с проводящими кластерами из-за накопления зарядов на границах кластеров. Электрическое поле этих зарядов экранирует внешнее поле внутри образца, и это воспринимается Рис. 8. Частотная зависимость действительной е' (1) и мнимой е'' (2) компонент диэлектрической проницаемости: а) - образец состава BeO+30 мас. % TiO2(мкм); b) - образец состава BeO+20 мас. % TiO2(мкм)+1 мас. % TiO2(нано) Fig. 8. Frequency dependence of real ε’ (1) and imaginary ε’’ (2) components of dielectric constant: a) – a sample of the composition BeO + 30 wt. % TiO2 (pm); b) - sample of BeO + 20 wt. % TiO2 (pm) + 1 wt. % TiO2 (nano) – 376 – в эксперименте как кажущееся увеличение действительной компоненты диэлектрической проницаемости [21]. Возрастание мнимой компоненты диэлектрической проницаемости в основном обусловлено наличием сквозной проводимости и определяется следующей формулой: ст'(®) ^(® )= (5) 8 0 ■ to где е0 - электрическая постоянная [22]. В пределе Q^ 0 е”(ю) ^ да, а с ростом частоты процесс накопления зарядов уже не возникает и диэлектрическая проницаемость стремится к стационарному значению показателя преломления е„. Приведенные на рис. 8a, b частотные зависимости действительной и мнимой компонент диэлектрической проницаемости хотя и уменьшаются с ростом частоты, но даже на высоких частотах f ~ 107 - 108 Hz все еще имеют огромную величину - е’ ® 760 и 220 соответственно. Это означает, что процесс диэлектрической релаксации захватывает область сверхвысоких частот и сопровождается поглощением СВЧ-поля [23]. Следует отметить, что выявленные большие значения действительной и мнимой компонент диэлектрической проницаемости не реальные параметры материала, а некоторые эффективные величины, возникающие из-за неравномерного распределения электрических зарядов и поля в веществе. Более корректные результаты измерений диэлектрических характеристик получаются в области высоких частот f ≥ 105Hz, где уже начинают выявляться релаксационные максимумы в частотных зависимостях е’’(ю) в области частот 107 - 108Hz (рис. 8a, b). Не исключено, что на других образцах керамик в зависимости от технологических режимов их синтеза процессы диэлектрической релаксации и поглощение энергии электрического поля могут находиться и на более высоких частотах в СВЧ-области. В области низких частот реальные диэлектрические характеристики исследуемой керамики искажены наличием свободных зарядов и сквозной проводимостью. Однако получить более реальные представления об электрофизических характеристиках данной керамики возможно, если устранить маскирующее влияние сквозной проводимости на диэлектрические спектры. Заключение Получены образцы (ВеО+ТЮ2)-керамики с содержанием добавок диоксида титана, имеющего микронные размеры, и с добавлением нанопорошка TiO2. Результаты растровой электронной микроскопии показали достаточно эффективное перемешивание компонентов шихты в специально разработанном реакторе импеллерного типа, в дистиллированной воде в условиях непрерывного барботирования сжатым воздухом. В образцах керамики с добавкой наночастиц структурные элементы TiO2 значительно меньших размеров по сравнению с образцами ВеО+ТЮ2, где добавка диоксида титана имела микронные размеры. Экспериментально установлено, что образец состава BeO+20 мас. % ТЮ2(мкм)+1 мас. % ТЮ2(нано) достигает максимальной плотности при температуре спекания 1520 °С, немного ниже температуры спекания, в котором диоксид титана представляет собой порошок микронного размера. Показано, что образцы керамики обладают электрической проводимостью, которая возрастает пропорционально угловой частоте с дробным показателем степени. Это позволило идентифицировать проводимость образца с микрочастицами как проводимость прыжкового типа. В образце с наночастицами TiO2 дисперсии проводимости не обнаружено, а наблюдаемый в эксперименте немонотонный рост проводимости с возрастанием частоты объясняется появлением релаксационной компоненты тока, сопровождающейся увеличением диэлектрических потерь. Установлено, что тангенс угла диэлектрических потерь для образца с микронным порошком TiO2 минимален на частоте f ~ 1 MHz, где реактивная компонента проводимости преобладает над активной компонентой. Максимум тангенса угла потерь этой керамики выявляется при подходе к частоте f ~ 100 MHz. На этой частоте активная компонента проводимости становится сравнимой с реактивной компонентой. Однако в образце с нанопорошком максимум угла диэлектрических потерь находится на более высоких частотах f > 100 MHz, что свидетельствует о наличии более значительных диэлектрических потерь на высоких частотах. Отмечено, что аномально большие значения действительной и мнимой компонент диэлектрической проницаемости в области низких частот связаны с наличием сквозной проводимости и поляризацией проводящих микро- и нанокластеров, входящих в структуру данных керамик. В дальнейшем для совершенствования известных объемных поглотителей СВЧ-энергии планируется детально изучить влияние различного количества добавок нанопорошка диоксида титана на изменение электропроводности керамики, ее импеданса, величины диэлектрической проницаемости и тангенса угла диэлектрических потерь в широком частотном диапазоне 1·102– 12·109 Гц и установить изменение коэффициентов ослабления СВЧ-излучения и стоячей волны по напряжению, определяющих способность керамики поглощать рассеянное СВЧ-излучение.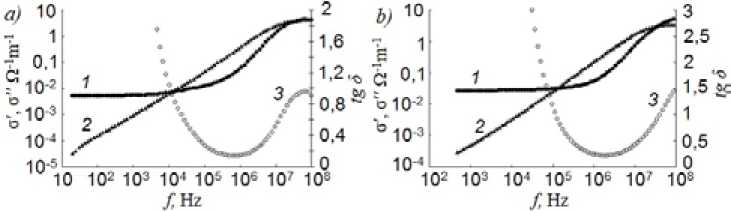
Список литературы Импедансная спектроскопия (ВеО+TiO2)-керамики с добавкой наночастиц TiO2
- Edelstein A.S., Cammarato R.C. Nanoparticles: Synthesis, Properties and Applications, Institute of Phisics Publishing, Philadelphia, 1996. P. 170.
- Кийко В.С. Влияние добавок диоксида титана на физико-химические и люминесцентные свойства бериллиевой керамики. Неорган. Материалы, 1994, 30(5), 688-693 .
- Беляев Р.А. Окись бериллия. М.: Атомиздат, 1980. С. 221 .
- Кийко В.С., Шабунин С.Н., Макурин Ю.Н. Получение, физико-химические свойства и пропускание СВЧ-излучения керамикой на основе ВеО. Огнеупоры и техническая керамика, 2004, 10, 8-17
- Кийко В.С., Горбунова М.А., Макурин Ю.Н. Микроструктура и электропроводность компазиционной (ВеО+TiO2)-керамики. Новые огнеупоры, 2007, 11, 68-74
- Kiiko V.S. Transparent beryllia ceramics for laser technology and ionizing radiation dosimetry. Refractories and Industrial Ceramics, 2004, 5(4), 266-272.
- Gorbunova M.A., Shein I.R., Makurin Y.N., Ivanovskaya V.V., Kijko V.S., Ivanovskii A.L. Electronic structure and magnetism in BeO nanotubes induced by boron, carbon and nitrogen doping, and beryllium and oxygen vacancies inside tube walls. Physica E-Low-Dimensional Systems & Nanostructures, 2008, 4(1), 164-168.
- Пат. 2326091 RU С2 С 04 В 35/08. Способ получения электропроводной керамики на основе оксида бериллия. Ивановский А.Л., Кийко В.С., Акишин Г.П. Макурин Ю.Н.; заявитель и патентообладатель ГОУ ВПО УГТУ-УПИ и ИХТТ УрО РАН; опубл. 10.06.2008
- Медведев М.И. Сцинтилляционные детекторы. М.: Атомиздат, 1977. 235 с.
- Landmann M., Rauls E., Schmidt W.G. The electronic structure and optical response of rutile, anatase and brookite TiO2. Journal of Physics: Condensed Matter., 2012, 24(19), 1-6.
- Thompson T.L., Yates J.T. Surface Science Studies of the Photoactivation of TiO2 -New Photochemical Processes. Chemical Reviews, 2006, 106(10), 4428-4453.
- Tang H., Prasad K., Sanjines R., Schmid P.E., Levy F. Electrical and optical properties of TiO2 anatase thin films. Journal of Applied Physics, 1994, 75(4), 2042-2047.
- Кузнецов М.В., Кийко В.С., Ивановский А.Л. Рентгеновская фотоэлектронная спектроскопия сложной оксидной керамики: BeO-TiO2-C. Стекло и керамика, 2010, 10, 16-21
- Ушаков А.В., Лепешев А.А., Карпов И.В., Крушенко Г.Г. Физико-химические свойства порошка TiO2, полученного в плазмохимическом реакторе низкого давления. Технология металлов, 2012, 10, 27-32
- Кийко В.С., Макурин Ю.Н., Ивановский А.Л. Керамика на основе оксида бериллия: получение, физико-химические свойства и применение. Екатеринбург: УрО РАН, 2006. С. 324-332
- Беляев Б.А., Дрокин Н.А., Полубояров В.А. Исследование электрофизических характеристик катион-замещенной керамики гексаалюмината бария методом импедансной спектроскопии. Физика твердого тела, 2018, 60(2), 269-275
- Ross Macdonald J. Impedance Spectroscopy. Annals of Biomedical Engineering, 1992, 20, 289-305.
- Pradhan D.K., Choudhary R.N.P., Samantaray B.K. Studies of dielectric relaxation and AC conductivity behavior of plasticized polymer nanocomposite electrolytes. International Journal of Electrochemical Science, 2008, 3, 597-608.
- Dyre, T.B. Schrøder. Universality of ac conduction in disordered solids. Reviews of Modern Physics, 2000, 72(3), 873-892.
- Kiiko V.S., Gorbunova M.A., Makurin Yu.N., Neuimin A.D., Ivanovskii A.L. Microstructure and electric conductivity of composite (BeO+TiO2) ceramics. Refractories and Industrial Ceramics. 2007, 48(6), 429-434.
- Jianjun Liu, Chun-gang Duan, Mei W.N., Smith R.W., Hardy J.R. Dielectric Properties and Maxwell-Wagner Relaxation of Kompounds ACu3Ti4O12 (A = Ca,Bi2/3,Y2/3,La2/3). Journal of applied physics, 2005, 98, 093703, 093703-1-093703-5.
- Bordi F., Camettiand C., Colby R.H. Dielectric spectroscopy and conductivity of polyelectrolyte solutions. J. Phys. Condens. Matter., 2004. 16, 1423-1463.
- Ненашева Е.А., Трубицына О.Н., Картенко Н.Ф., Усов О.А. Керамические материалы для СВЧ-электроники. Физика твердого тела, 1999, 41(5), 882-884


