Implementing Blind De-convolution with Weights on X-ray Images for Lesser Ringing Effect

Published Online August 2016 in MECS

The main aim of restoration is to obtain the improved version of an image. Improvement is done in accordance with some predefined criteria. However enhancement is also improvement of image but it is subjective while restoration is objective. For example contrast stretching is enhancement and deblurring an image is restoration. Restoration actually models the degradation and applies the inverse to get the improved image[1][2][3][4]. But they do have overlapping areas. There are several restoration techniques[5][6] and can be broadly classified into Blind and Non-Blind techniques. Blind techniques try to restore images without having any knowledge of the blur operator (PSF). Non-Blind techniques have knowledge about degradation, i.e. they know the blur operator (PSF). Example of Non-Blind technique is Lucy-Richardson Algorithm(LRA) and that of Blind technique is Blind Image Deconvolution (BID). Point spread function (PSF) is the degree to which an optical system blurs (spreads) a point of light[7]. The PSF is the inverse Fourier transform of optical transform function (OTF) in the frequency domain. The OTF describes the response of a linear, position-invariant system to an impulse. OTF is the Fourier transfer of the point (PSF) [8]. In such applications the degradation is inevitable as the intensity of the X-ray radiation is reduced so that there is minimum damage done to body of the patient[9].

Blind Image Deconvolution can be divided in two different categories according to the approach they follow[10]. They are A priori blur identification methods and Joint Identification methods . In the first approach the PSF is first identified from the image and then any of the classical restoration technique is used to get the distortion free image. In the second approach the PSF and the image are identified simultaneously. Majority of the blind techniques follow this approach.

• A.    X-ray Images

Image Restoration has played an important role in the field of medical imaging. There are numerous medical images out of which one is the popular X-ray Image. X-rays are one of the oldest source of electromagnetic radiation used for imaging. The best known use of X-ray images so far are the medical images[1]. X-ray images are taken by placing the patient between the X-ray source and a film sensitive to X-ray energy. When the X-rays are passed, the intensity of X-ray is modified by the body of the patient as it is absorbed more at some parts within the body and less at some other parts. The resultant X-rays which fall on the film actually develop the image. Two X-ray images have been shown in Fig. 1. Digital form of the X-ray image is obtained either by digitizing X-ray film or letting the resultant X-rays fall directly on devices that convert X-rays to light. One such device which converts X-rays to light is the phosphor coated screen. During this acquisition process some distortions come along in the image. These distortions are blur and noise much like motion blur and Gaussian noise respectively[11]. Therefore an X-ray image needs to be restored to remove the distortions as much as possible.

• B.    Ringing Effect

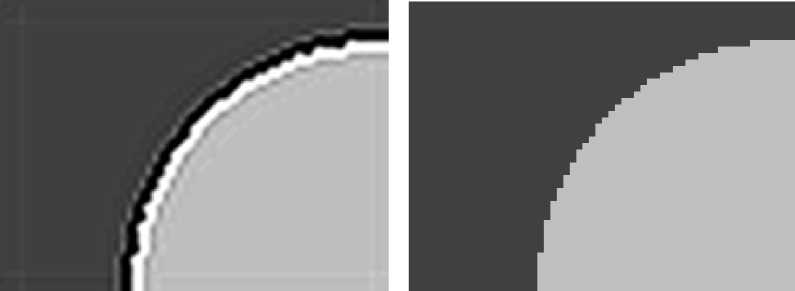
Ringing effect or Gibbs phenomenon is an annoying appearance which occur as rippling artifact near the edges in images and videos. It occurs due to loss or misrepresentation of high frequency components in the image. It can be experienced in variety of images like medical images, over sharpened images, compressed images, holographic images, images transmitted over analog channel, etc. Ringing artifact is actually a side- effect of many image processing techniques. All the restoration techniques which make use of fast fourier transformation suffers the inclusion of ringing effect in the image. Due to the linear space invariance assumption the restoration algorithms are implemented uniformly across the entire image. This results in uniform amplification of the high frequency components and thus the ringing effect occurs. The ringing effect is shown in images in Fig. 2.

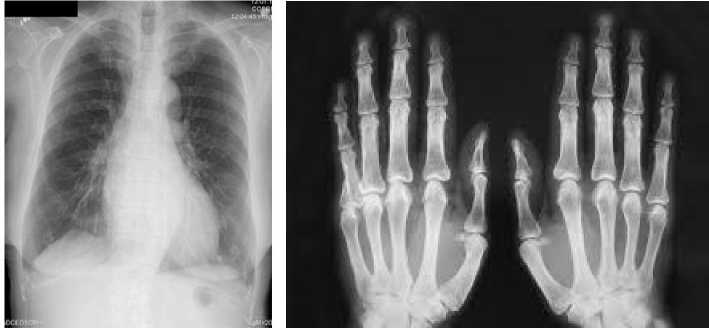
(a) Chest                                         (b) Fingers

Fig.1. X-ray Images

• C.    Blind Deconvolution Algorithm

There are many new and old Blind Deconvolution algorithms. The following algorithm is one of the early Non-Bayesian, Non-parametric iterative blind deconvolution algorithm [10]. This algorithm restores the image and PSF simultaneously by improving them iteration after iteration. Proposed by Ayers and Dainty [12] it begins with an initial random PSF estimate h₀(x) and image estimate f₀(x^) and at iteration i , it goes through the following steps:

• 1.    Determine F( k), the DFT of fi(x).

• 2.    In the Fourier domain impose the blur constraints:

  h ^k) =

  
  

• 3.    Determine h_t(x), the IDFT of H_t(k).

• 4.    Spatial domain positivity and finite support constraints imposed on h_t(x) to give h_t(x).

• 5.    Determine H_t(k), the DFT ofh_t(x).

• 6.    Image constraints imposed in Fourier domain:

• 7.    Determine ft(x) the IDFT of F(k)

• 8.    Spatial domain positivity and finite support constraints imposed on f(x) to give f_{+ +} i (x).

• 9.    Go to step 1 for next iteration, i=i+1 .

G (k)F-'( k) №№ + а/\Й 1_ _г\ 2

where(. ) * indicates complex conjugation.

p     ₌      G(^k)HT(^k)

^t(k) |Я_i( k)p + a/|F_;(k)| 2

The real constant a is the energy of the additive noise and must be properly chosen to get proper restoration result. The algorithm is also sensitive to initial guess[13].

• II.    Implementation of Bid on X-Ray Images Using Matlab

The image shown in Fig. 1(b) is taken for experimentation. The image is prepared by adding Gaussian noise and motion blur[14]. The resultant image is shown in Fig. 3. Using matlab, Blind deconvolution is applied on the image in Fig. 3. Two restored images are shown in Fig. 6, one without using edgetaper function and the other one with using edgetaper function. Total number of iterations taken is twenty. Function edgetaper is used to suppress the ringing effect. Generally the ringing effect occurs along the sharp intensity changes and along image borders and it appears in all those images restored by deblurring algorithms which use Discrete Fourier Transform. Actually the function edgetaper is used before implementing blind deconvolution and basically it blurs the edges as per the given PSF resulting in lesser ringing effect. In both the images of Fig. 6, ringing effect is more prominent at the bottom. A careful observation will reveal that image in Fig. 6(b) has a slightly lesser ringing effect which is proved by a metric later.

(a) Image with ringing effect                  (b) Same image without ringing effect

Fig.2. Ringing Effect

The edgetaper function does not eliminate the ringing effect totally therefore further refinement can be done to restore the image more close to the original.

• III.    Basics for the Proposed Method

• A.    Edge operators

Edge operators are filter masks which detect the edge points in an image. The mask is centered at every pixel of the image and response or output is obtained by computing the sum of products of mask coefficients with the corresponding image coefficients lying within the area encompassed by the mask. There are several edge operators but Sobel operator is chosen as it gives smoothing effect to greatest extent in the image. Sobel operators are as shown in Fig. 4[1].

• B.    Morphological Operations

The standard binary morphological operations are dilation and erosion. Dilation and erosion are operations which work by translating a structuring element (like a mask or kernel) over the binary image and examining the intersection of the structuring element with the image pixels. Examples of structuring elements are shown in Fig. 5.

Dilation: In dilation at each shift if there is any intersection of similar pixels (pixels with intensities 1) then the intensity of the pixel under the center of structuring element is changed to 1 [2]. If X be an image and B be the structuring element then the dilation of X by B is set of all shifts, z such that B and X overlap or intersect by at least one element. It can be written equivalently as

X ®S = {z |[(s)znx] ex} (3)

where В is the rotated image of B.

Erosion: In erosion at each shift if there is no complete overlapping of similar pixels (pixels with intensities 1)then the intensity of the pixel under the center of structuring element is changed to 0 [2]. If X be an image and B be the structuring element then the erosion of X by

B is set of all shifts, z such that B is contained in X. It can be written equivalently as

xe в = {zi(B)_z ex}           (4)

-1	-2	-1
0	0	0
1	2	1

-1	0	1
-2	0	2
-1	0	1

(a) Horizontal                         (b) Vertical

0	1	2
-1	0	1
-2	-1	0

-2	-1	0
-1	0	1
0	1	2

(c) Diagonal (+45°)                 (d) Diagonal (-45°)

Fig.4. Sobel Operators

1	1	1
1	1	1
1	1	1

1

1

1

(a)                         (b)

Fig.5. Structuring Elements

(c)

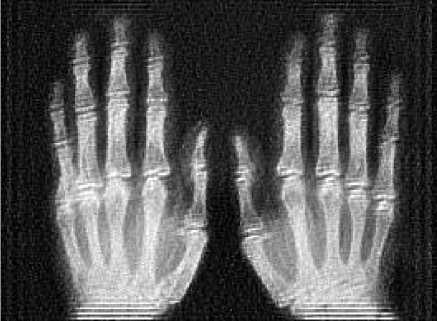
(a) Edgetaper not used

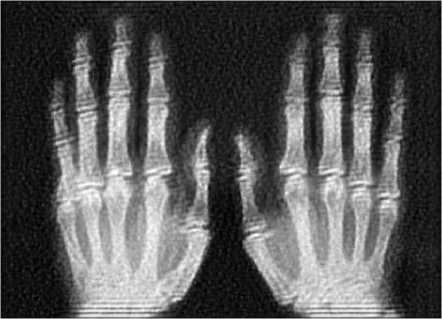
(b) Edgetaper used

Fig.6. Restored Images

• IV.    The Proposed Method: Bid with Weights

The proposed method for greater reduction of ringing effect in BlD restored X-ray images is as given below:

• A.    Detection of Edge points

Edge points are detected using Sobel operator. The Sobel operator is implemented on the image shown in Fig. 3. The resultant image is a binary, black and white image with white pixels (pixels with intensities 1) being the edge points and black pixels (pixels with intensities 0).

• B.    Dilation of Binary Image

Dilated version of the resultant binary image in step 1 is obtained. The structuring element used in the dilation process is as shown in Fig. 5(b). Dilation is done to broaden the edges. The resultant image of this step again is binary image but with pixels just adjacent to white pixels also being white.

• C.    Assigning Weights to pixels

As the ringing effect occurs at edges and along image borders so these points or pixels are designated with weights 0(zero) and others with 1(one). In other words all the white pixels of the dilated image are assigned weights 0 and black pixels weights 1. In addition to this, three rows/columns of pixels nearest along the border are also assigned weights 0.

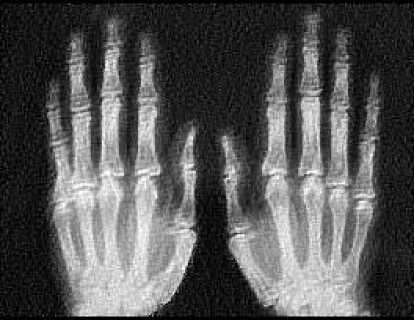
Fig.7. Restored Image obtained with the proposed method

• D.    Restoration with BID with Weights

Blind deconvolution with weights is now implemented on the image as in Fig. 3 and the restored image is as shown in Fig. 7. Visually, hardly any ringing effect is seen whereas image shown in Fig. 6(b) the ringing effect is very very prominent. Actually in the proposed method the pixels with weights 0 are not at all considered in the restoration process.

• V.    Metric for Evaluating Ringing Effect

The metric chosen for quantitative measurement of ringing effect is Edge Content. Basically Edge Content [15] computes the edges and we know that the more the edges in an image more is the ringing effect. Therefore this metric is used for the confirmation of the proposed method.

• A. Edge Content (EC )

Considering an image A(x,y) where x is row coordinate and y is column coordinate. The gradient vector at any pixel location (x,y) is given as

(Х,^

дА (х,у) = 11=                  (5)

(х. У)

where

Gx = А(х.у) - А(х + 1,у)

Gy = А(х,у) -А(х,у + 1)

The absolute value of image gradient is

|5А | = 7 G^ + Gy2                  (6)

The metric EC is defined as

^ЕС =^^#А(х,у)1        (7)

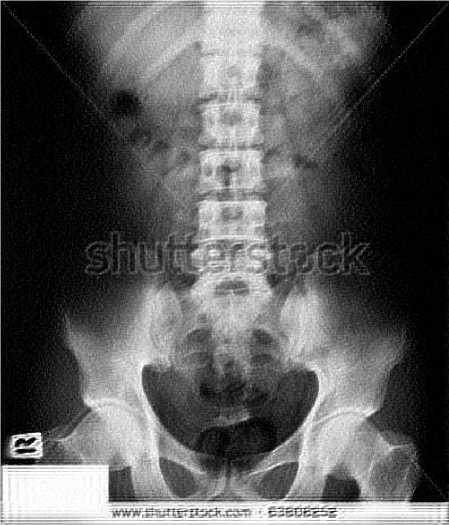
(a)Abdomen(BID without Weights)

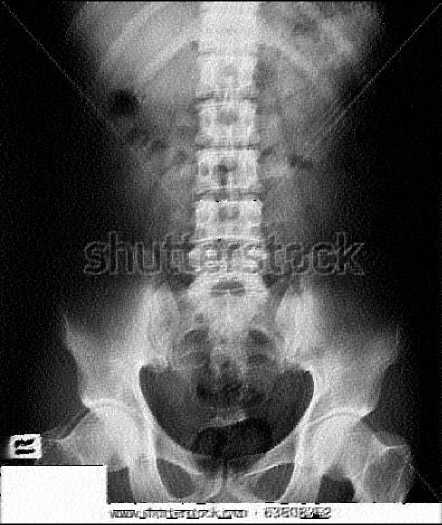
(b)Abdomen(BID with Weights)

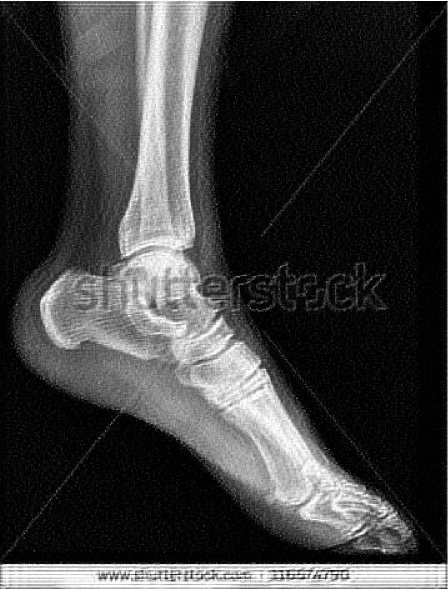
(c)Ankle (BID without Weights)

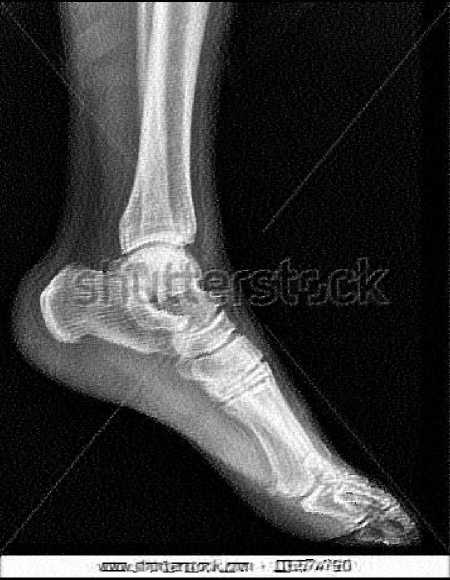
(d)Ankle (BID with Weights)

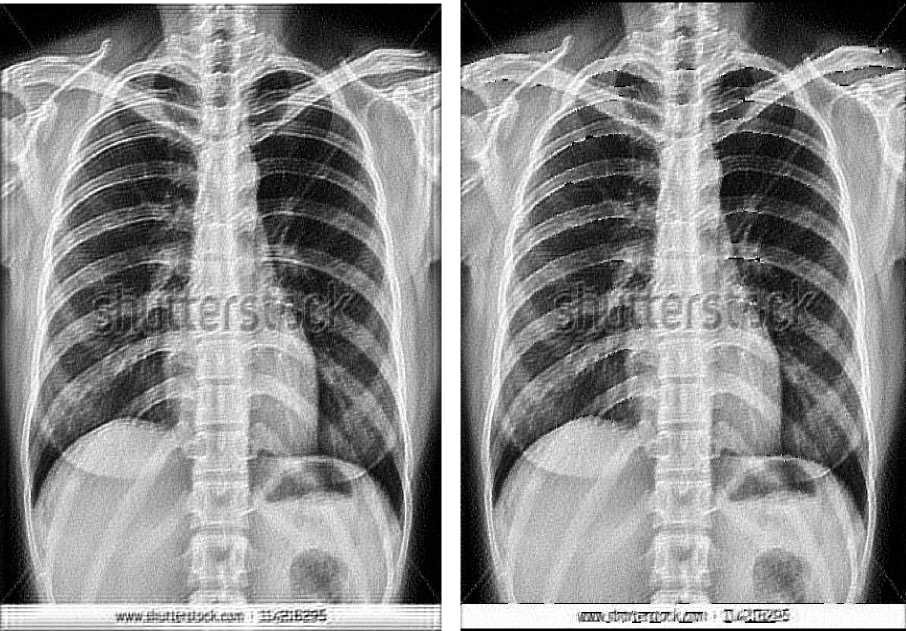
(e)Chest (BID without Weights)                            (f)Chest (BID with Weights)

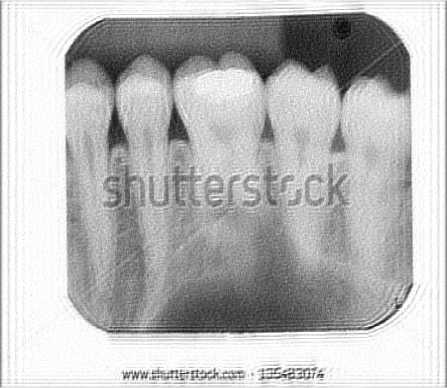
(g)Teeth (BID without Weights)

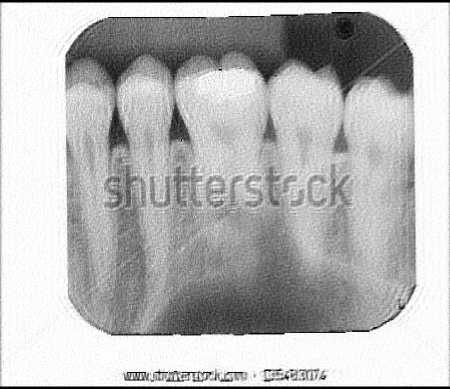
(h)Teeth (BID with Weights)

Fig.8. X-ray Images restored using BID with and without Weights

where m x n is the size of image and

• (ii)    BID with Weights (Fig. 7)

EC = 13.0177

As per the formula of EC the following values are obtained:

VI. Results

• (i)    BID without Weights (Fig. 6(b))

EC = 13.3136

As it can be seen from the results that EC of the X-ray image restored using BID with weights is less than that of the one using BID without weights. Visually it is difficult to make out the presence of any ringing effect anywhere in the image shown in Fig. 7. Thus it can be concluded that X-ray images restored using BID with weights have lesser ringing effect than those restored using BID without weights. Just to check for consistency and correctness of the proposed method, some more X-ray images[16] are taken for experiment and their results and corresponding images are given in Table 1 and Fig. 8 respectively. In all the images the values of EC by implementing the BID algorithm with weights are less than the ones by implementing BID algorithm without weights.

Table 1. EC values

S. No.	X-ray Image	BID without Weights	BID with Weights
1	Fingers	13.3136	13.0177
2	Abdomen	10.6042	10.5546
3	Ankle	10.6745	10.2605
4	Chest	14.5468	14.4973
5	Teeth	11.1853	11.1303

• VII. Conclusion

From the results obtained in Table 1 and the images obtained in Fig. 8, it can be concluded that the proposed method is better. Actually by default all the pixels have weights 1, i.e. all the pixels are treated equally. When a pixel is to be totally discarded from consideration it is assigned weight 0. Any weight within the interval [0, 1] can be assigned depending on how much the pixel is to be considered or neglected. The less the value for weight chosen the more is the pixel neglected. Therefore for maximum reduction of ringing effect the weight should be chosen as zero.