Implementing of microscopic images mosaic revising algorithm

Image stitching is a hot topic for the computer vision field and creating an accurate panoramic mosaic image automatically and quickly is a main research topic at present, i.e. establishing large aerial and satellite photographs; increasing a camera's vision field and resolution; setting virtual reality environment and measuring microscopic images [1] etc. While stitching several adjacent images into an integrated one, it is required that splicing areas transit naturally without any seams in color and structure. In general, there are usually two types of seams between images, one is differentiated brightness gap caused by uneven light exposure, the other effect results in geometric structure gap showing dislocation, overlapping and separation caused by image distortion or image registration error.

As to geometric structure gap, literature[2] has

This research is supported by Zhejiang Province Education Department Foundation of China under Grant No 20050836.

analyzed its formation, which may be caused by the relative data changes in the overlapping parts of two images due to comparative small rotation of the image’s overlapping parts during image data acquisition, or by focal distance changing while focusing target moving, which lead to adjacent images data variance. The subsequent variation is difficult to correct.

Image registration can be classified into two types, one is sequential, and the other is global. While using 2D image acquisition scan mode, frame to frame method will cause accumulation of the adjacent image alignment errors, resulting in mismatching. To reduce the accumulated error, some global optimization methods are used for the image stitching by adjusting all alignment parameters, the error accumulating in the image mosaic can be eliminated effectively [3-9]. Jia [10] use the structured approach to deform dislocation structure, which will produce distortion of the image structure. A strategy [11] of transformation reference image is adopted, although this can avoid the accumulated errors in continuously stitching, but the partly region in the final image needs several mathematical conversion, thus will lead to image distortion. A GIST method is presented by Levin [12], which optimizes the gradient strength of the overlap region to achieve the image mosaic. However, these methods are limited for dealing with serious structure dislocation and unable to process large scale image mosaics effectively and theses methods are also slow in speed. Moreover, while overlapping areas of the images have less information or initial parameters are highly uncertain, significant amount of error might occur and is in need of frequent manual intervention and repetitive adjustment.

As indicated in the preceding discussion, those image stitching methods which are effective in certain ways still have room for improvement regarding processing speed and effectiveness, particularly in precision. Literature [13] proposes the basic principle for images mosaic revising, that is while the four adjacent images were stitched correctly; correlations between their relative positions will emerge. When three images can be correctly spliced, the fourth one will finds its correct position accordingly.

Therefore mismatch for one pair of images can be fixed. This law is of great significance for applications in difficult data acquisition or high accuracy level splicing. But in actual application, it is difficult to operate since the same error can take place in splicing rows or columns, also in horizontal and vertical interleaving, even caused by former mosaic errors.

In this article, we propose an image stitching revising algorithm based on the relevant correlations of the positions between adjacent image mosaics. First, we will define the mosaic unit and put forward the equations of splicing parameters and intellectually parameters simplifying regularities for larger image mosaic, then we will describe the processing of the revising algorithm in detail. An experiment result and analysis are provided in later sections, which will show the approach is effective in revising the error matching in microscopic images mosaic. In order to highlight the core method of image stitching without losing sight of practical application, this paper focuses on pathological microscope image stitching, through which those data changes only by relatively small rotations or the target is re-focused twice after moving are simply attributed to splicing error processing.

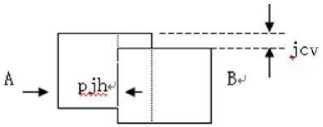
Figure1 Horizontal splicing

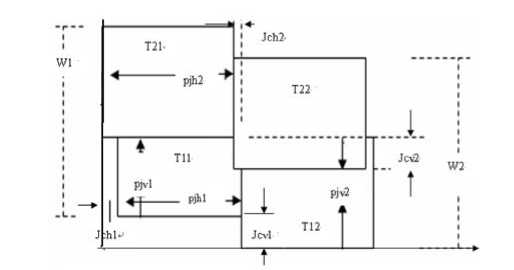
Four neighbor image splicing

II Principal and algorithm of images mosaic REVISING

• A.    Multi-position relationship of image mosaics

The image mosaic is processed from the horizontal and vertical direction. As long as two images are stitched successfully, the uniform area should be overlapped. Fig.1 is a horizontal stitching case, and the horizontal splicing column of graph A is named pjh , which is the projection of the initial vertical edge of graph B. The jcv denotes vertical interleaving distance, which is the vertical diverge distance of the overlapped area by horizontal stitching. Similarly, vertical stitching, the pjv denotes the row of vertical splicing and jch denotes the horizontal staggered distance.

When considering the four adjacent images splicing with two rows and two columns, there are two horizontal and two vertical stitching. Shown in Fig.2, where T11, T12 and T21, T22 are the first row and second row of the horizontal adjacent images, let pjh1 , jcv1 and pjh2 , jcv2 denote their horizontal splicing columns and vertical interleaving distance respectively. Where T11, T21 and T12, T22 are the first and second columns vertically adjacent image, let pjv1 , jch1 and pjv2 , jch2 denote two vertical splicing rows and two horizontal staggered distance respectively. Above the four adjacent images form an independent mosaic unit, according to their relative of the location, there are following equations.

pjh1= pjh2-jch1+jch2.                (1)

pjv1= pjv2-jcv1+jcv2.                 (2)

Equation (1) and (2) can be proved easily, using the relationship between the positions in Fig.2. Let the size of each image in Fig.2 is set to L × L, from Fig.2 can get the following relationship:

w1=L+pjv1.                      (3)

w2=L+pjv2.                      (4)

Where w1 is the image width after the first row stitching and w2 is the image width after the second row stitching. According to the Fig.2, also get following equation.

w2-(-jcv1) =w1 - (-jcv2).              (5)

In general, in Fig.1 and Fig.2, jcv moves down (or left) shifting as a negative, otherwise moves up (or right) as positive. While absolute value is used in deriving (5). Now in Figs 1 and 2, the jcv is moving down so that it is negative. As long as w1 and w2 are substituted into (5), the following equations can be gotten.

L+pjv2+jcv2-jcv1 ＝ L+pjv1, pjv2= pjv1+jcv1-jcv2 , so that the (2) is proved. Similarly, (1) can be proved.

• B.    Basic characteristics of splicing

According to the basic relation of image mosaic there are following properties.

The property 1. The horizontal stitching column and vertical stitching row determined the stitching positions along the splicing direction which will affect the overlap situation, while the row or column will be reduced by more overlaps or increased by fewer overlaps. Moreover, the horizontal and vertical interleaving situation relate to the staggered distance in the vertical stitching direction, shown as Fig.3.

The property 2. Equation (1) and (2) are independent and represent the horizontal and vertical alignment situation. When splicing correctly, the (1) and (2) are established, by contraries, is not true, since each equation, if and only if, the three parameters are determined, then it has a unique solution.

The relationship between splicing parameter and interleaving distance should meet (1) and (2), otherwise, are subject to revision. The amount of revising called parameter modified weight which can be reasoned from (1) and (2) directly.

Xh=pjh2-pjh1+jch2-jch1.              (6)

Xv=pjv2-pjv1+jcv2-jcv1.              (7)

Where Xh and Xv denote the weight of parameter MODIFIED IN HORIZONTAL AND VERTICAL MOSAIC direction, which reflecting the stitching state. While the weight is zero, (1) and (2) come into EXISTENCE AND THE PARAMETER DO NOT NEED modification generally. Eq.(1) and (2) and some of THE ABOVE PROPERTIES WILL BECOME THE PRINCIPAL AND revising splicing bas is .

Ш Implement of the revising algorithms

As analysis in preceding section, since there are multiple solutions to (1) and (2), of which only one is appropriate, and therefore it is essential to reduce the changeability of the variables.

• A.    Evaluation of the revised results

The revised parameters describe the stitching state of each mosaic unit, which can be evaluated with the Least

Squares, that is, when the summation of the parameter revised value is the minimum, the image stitching error

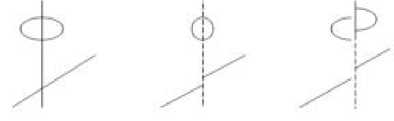
correct              overlap vertical interleaving

Figure 3. Image stitching states is the least and the stitching state is the best. The equation is as following.

P T^mii^ pjh - pjh + jch - jch )² + (pjv — pj v + jcv — jcv ² • ⁽⁸⁾ y11 = 1

Where in (8), the two brackets are the stitching parameters of level and vertical in a mosaic unit, y and x mark the location of the unit, when PR is minimum or equal to zero that means the revising is complete. However, as (8) is based on the (1) and (2), from previous analysis, (1) and (2) should have multiple solutions in order to reduce the variability of the parameters.

The literature [8] shows that in the mosaic units as long as three images are spliced correctly, the fourth one on the map will also be correctly spliced. Figs.1 and 2 show that there are eight parameters among four images in graphs, when three pairs of images, T11 and T12, T21 and T22, T11 and T21, can be correctly spliced, then pjh1, jcv1, pjh2, jcv2, pjv1, jch1, a total of six parameters are known and the pjv2 and jch2 can be calculated respectively with (1) and (2) according to the known parameters. Hence, the above conclusion is correct.

• B.    Simplifying the revising algorithm

• 1)    Processing the first row and column. While splicing several individual images into an integrate one, image positioning is the key point, which means one of the splicing positions in the horizontal and vertical splicing direction is determined. Since the starting position also affects the splicing process, the starting edge and sequence stitching denote the splicing position. Mosaic unit of Fig.2 shows that in the T11 the jch1 and jcv1 determine the horizontal and vertical position, if jcv1 protrudes upward, take jcv1 as an initial value, otherwise jcv1 = 0 (taking the edge of T11 as the initial value). Therefore, the position variables of T11 should be modified as y + jcv1 , x + jch1 . Considering these parameters will possible change during processing, usually first consider the possible changes within ± 2, if the results do not meet the requirements, then expanded them, anyway the parameters are still variable. Specific treatment should be considered when there are variable parameters, so further simplification is required.

Due to the splicing position mismatch, the image mosaic error may be caused by the adjacent images staggering in distance, excessive or owe overlapping, even complicated mixture. In order to limit the variety of variables, by analyzing the regularity of level and vertical edge changes in image splicing and validating with experiments, we summarized the following simplified rules (ref. Fig.2).

• a)    Revising parameters jch1, jcv1 . The jch1 and jcv1 determine the horizontal and vertical positions (starting position) of T11. If the image mosaic error is caused by jch1, jcv1, the adjacent images will stagger in distance along the splicing line of the pjh1 and pjv1 and we will get following simplified rules..

Rule 2, while the images between pjv1 , which is splicing line of T11 and T21, stagger in distance along level splicing, modifying the jch1 only.

It can be deduced that the vertical staggered parameter is the location basis in the vertical direction of the first row in the image and horizontal one is the one in level direction.

• b)    After modification, the values of jch1 and jcv1 can be considered as constant and we can get the other simplified rules as following.

Rule3, while the images between pjh1 are excessive or owe overlapping and adjacent images between pjv2 stagger in distance along level splicing simultaneously, modifying the pjh1 .

Rule4, while the images between pjh2 are excessive or owe overlapping and adjacent images between pjv2 stagger vertically simultaneously, modifying the pjh2 .

Rule5, while the images between pjv2 stagger in distance along level splicing, if there is no excessive or owe overlapping along vertical splicing, modifying the pjh2, otherwise modifying pjh1.

Like the same approach, the other simplifying rules to process the horizontal staggering and excessive or owe overlapping for vertical stitching.

• 2)    The outline of algorithm for processing the first row and column.

The kernel algorithm for processing first row and the first column is as following.

For (i=1, j=1; j<=n; j++) // first process jcv1 of the //first row, then the rest.

• {    If (j unit between pjhl stagger vertically and i==1 ) modifying jcvl ;

If (j unit between pjh1 excessive or owe overlapping and pjv2 stagger vertically) modifying p jv1 ;

Else if (j unit between pjh2 excessive or owe overlapping and i=2, and the unit of j=j+1 stagger vertically) modifying pjh2 ;

Else if (j unit between pjh2 stagger horizontally) {if (the images between pjh1 no excessive or owe overlapping vertically) modifying pjh2 else modifying pjv1 }

}

Similarly, processing the first column. First processing the jch1 of the first row.

For (j=1, i=1; i<=n;i++) if ( i unit between pjv1 stagger vertically ) modifying jchl ;

For (j=1, i=1; i<=n; i++) //processing the rest.

• {i f (i unit between pv1 stagger vertically and j=1) modifying jch1 ;

… }

Since jcv1 and jch1 is the base and independent for splicing, they should be processed first, and the modification for the other parameters can be determined by the function based on simplifying rules. For improving the efficiency, the simplifying rules of considering multiple mosaic units should be added. After processing for the first row and the first column, the parameters on the left and down of each unit in the parameter table should be treated as constant values.

• 3)    Processing T22 directly while splicing the mosaic unit. Known from previous sections, except for the first row and first column, the left and down parameters in each unit of the parameter table is constant, so following the splicing order, the parameters in processing unit have been modified except for related to T22, so that the processing mosaic unit can be transformed to splice the T22 directly. It may be related to both vertical and horizontal stitching which can be determined by (6) and (7), if Xh=0 there is nothing to do for pjh2 , only need to modify pjv2. If Xv=0 , only need to modify pjh2 . Thus parameter selecting has been simplified further.

• 4)    While the parameters in the unit which Xh=0 and Xv=0 , modification is unnecessary except for mismatch.

After above simplification, variability of the parameters can be basically limited in one or two parameter, thus greatly reducing the computational complexity, making revision possible. At last, the remaining parameter will be selected with aided by eyesight.

• C. Process of the revising algorithm

The gist of realizing the revising algorithm is described as following.

• a)    Enlarging the mosaic image, marking the error stitching places on the mosaic image, and the stitching rows and columns between any two images.

• b)    Checking the error in the revising value table, even the zero unit also can exist the splicing error and vice versa.

• c)    Above all, revising first row and first column following the stitching order from top to bottom and left to right.

• d)    The middle unit is also revised following the stitching order which modified the pjv2 and pjh2 mainly.

• e)    The revising only amend those value zero cell in revising table except for step b), after generally amending the value of corresponding cell in the table should be zero, otherwise to expand the scope of amendments.

For a clearer idea of the whole data streams, we constructed a main work flow chart as shown in Fig.4.

• a)    Creating the parameter file. According to the selected image group, in initializing, the image stitching orders is from left to right and down to top while splicing adjacent images in level and vertical direction. The generated parameters should be recorded into the file, and the revised stitching parameters can be pick up from the file by program initializing later, so that provide convenience for selecting different stitching images and subsequence revising.

• b)    Building the vertical and level parameter tables. For the sake of facilitating subsequent calculations, according to the splicing sequence, automatically generating the horizontal and vertical splicing parameter tables respectively with the mosaic unit form and lined sequentially, for instance, as shown in Table I and Table II, the parameters of one spicing unit in the left down cell of Table I are pjh1=375 , pjh2=374 , jch1=1 , jch2=1 .c) Forming parameters revised table. According to the level and vertical parameter tables, the corresponding revising value tables can be calculated by (3) and (4).

• d)    First of all, amend the first row and the first column, if no problem, amend the other one. While revising, according to the value in the revised parameter tables and simplified rules as well as the state of error match, generating several parameter groups and select a most appropriate one as splicing parameter.

W EXPERIMENT RESULTS

To verify the effectiveness and practicability of the revising algorithm, the image revising experiments of 20 group images, in which each group consisted of 16 images with the size of 512 X 512 and overlapped area about 100 pixels, was executed.

• A.    Experiment data and result of image in group B

Fig.5 is the original result of image splicing in B group. In order to facilitate inspection and correction, the following procedures are proposed:

• a)    Modifying the brightness of the adjacent images so as to check the gap easily.

• b)    In order to realize accurate splicing, this paper does not use smoothing, and the yellow flat circles denote the wrong stitching places. Magnification is used.

• c)    In order to facilitate inspection and correction, the horizontal and vertical splicing parameters are put together respectively to create two parameter tables automatically, shown as in Table I and Table II, which are composed of each unit splicing parameters and in turn. The pjh , and pjv in the table are the mosaic columns and rows respectively, jch and jcv are the horizontal and vertical staggered parameters.

Using (1) and (2) calculated and created the level and vertical modified weight tables automatically as shown in Table III and Table IV. According to Table III and Table IV, to check the stitching situation, if the value of item in the tables is not zero, usually has to modify the parameters of corresponding mosaic unit. The revised parameter table shown as Table V and Table VI.

• B.    Compared before and after revising

After revised by the above methods, the picture integrated by 16 images is basically intact. A comparison before and after revising is in the Figs.6-8. From left to right, in Fig.6, images 1 and 3 with yellow flat circles are error, images 2 and 4 are revised, in Fig.7, image 2 has been revised, in Fig.8, image 2 has been revised. As Figs.6-8 shown that the splicing mistakes have been modified perfectly.

• C.    Dealing with serious splicing errors in group S

There are more serious splicing errors in images of S group, even appearing hollow phenomenon in Fig.9. Table V and Table VI are the parameters revised value table. The upper left corner in the image confirmed mosaic unit with significant errors. However, from the tables, it can be found that the splicing errors are small in other parts, providing the possibility to correct.

For example, Fig.10 is the result of stitching the upper left corner, in the figure there are two significant horizontal and vertical gaps, and the stitching pattern on both sides are not similar at all, indicating that the stitched row and column involve a major error. Fig.11 is a revised image, comparing it with Fig. 9, it can be found that the stitched row and column on the mosaic unit of upper left corner of the picture have undergone great changes, which reflects the strong revising capability of algorithm.

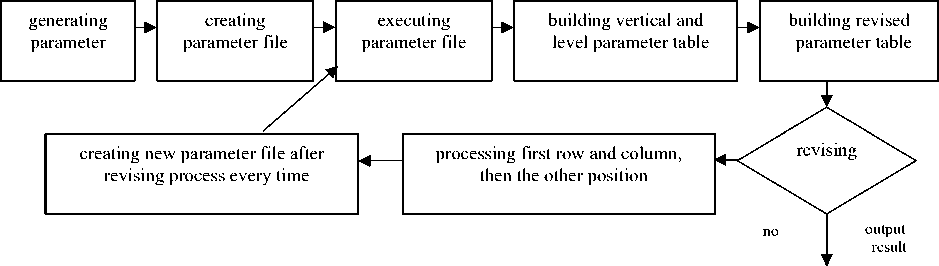
Figure 4 Revising algorithm working flow

TABLE I. level parameter table

jch	pjh	jch	pjh	jch	pjh	jch
	376		383		380
26	367	17	368	3	377	1
1	374	7	370	9	376	8
1	375	1	375	6	369	1
TABLE II.		VERTICAL PARAMETER TABLE
pjv	jcv	pjv	jcv	pjv	jcv	pjv
	1		1		1
363	1	363	1	364	1	364
359	-1	359	1	359	1	359
353		353		353		354
	1		1		1	0
	TABLE III.		L evel modified weight
		0	1		1
		-1	0		-1
		-1	0		2

Figure 5 Image stitched by 16 images

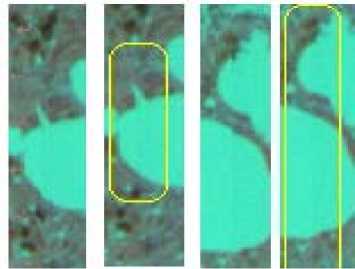
Figure 6 Image B stitched by level

TABEL № VERTICAL MODIFIED WEIGH T

0          10

2        00

• - 2         01

TABEL V LEVEL REVISED VALUE OF S

• - 36  -1211

1       10

• - 1     00

TABEL VI VERTICAL REVISED VALUE OF S

• - 27  630

• - 1      10

1     00

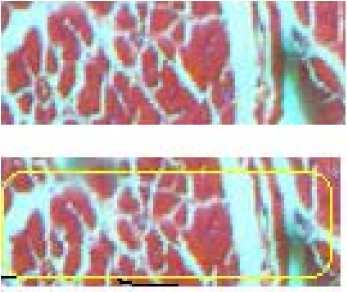
Figure 7 Image C stitched by vertical 1

Figure 8 Image C stitched by vertical 2

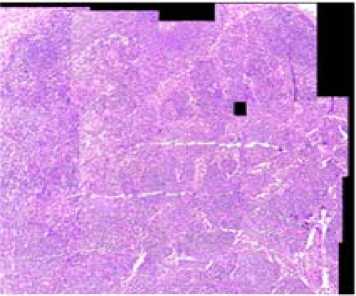
Figure 9 Original stitched image of group S

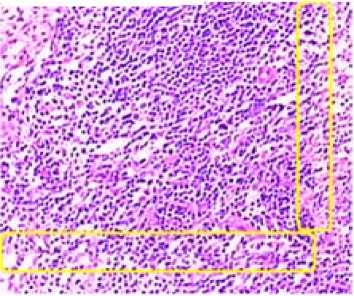
Figure 10 Upper left corner stitched errors in group S

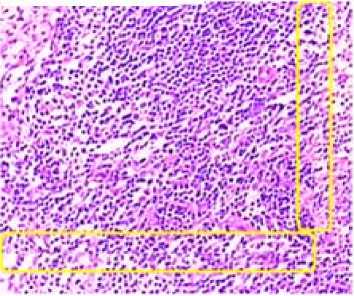
Figure 11 Revised stitched image of group S

V CONCLUSION

Through this experiment, the pathological mosaic images of 20 groups have been revised by the splicing revising algorithm that validates the algorithm with good results. Since the image stitching error can be controlled within one pixel, this algorithm is suitable for occasions requiring higher precision and involving difficult data acquisition, and it has a strong ability to revise mosaic image with effectiveness. In order to optimize the operation, the program based on the revising algorithm can calculate, display and revising automatically. Such shows the algorithms and approach are feasible. However, it is necessary to improve process automation for final parameters selection, especially with lager amount and higher precision which usually need visual assistance, and to expand the scope of stitching while optimizing the system.

ACKNOWLEDGMENT

We acknowledge professor Ping Zhang and Ms. Haiyan Zhang for scientific support. This research is supported by Zhejiang Province Education Department Foundation of China under Grant No 20050836.