Importance of S-Blocks in Modern Block Ciphers

Автор: Lisitskaya I.V., Melnychuk E.D., Lisitskiy K.E.

Журнал: International Journal of Computer Network and Information Security(IJCNIS) @ijcnis

Статья в выпуске: 10 vol.4, 2012 года.

Бесплатный доступ

There is a new approach to determine the degree of cryptographic S-boxes suitability. This approach is based on estimating the number of transformation cycles required for a cipher to achieve differential and linear nature of the state typical for random substitution of the appropriate degree. The paper presents the results of experiments to determine the differential and linear indicators of the Heys cipher (a cipher with a weak linear transformation) and a reduced model of the Rijndael cipher (the cipher with a strong linear transformation), using nibble S-boxes with different values of the XOR table differences maxima and linear approximations table displacements. It is demonstrated that, contrary to widely-known approach that links cipher performance indicators with strength indicators of substitutions that they use, the resistance to cipher attacks by means of linear and differential cryptanalysis (maximum differential and linear probabilities) does not depend on S-boxes used. It is concluded that random substitutions can be used as the S-block designs without compromising the performance of cryptographic ciphers. It means that the search for S-boxes with high encryption performance (at least for ciphers with strong linear transformations) is an unpromising task. At the same time it is shown that a good cipher can not be built without a nonlinear transformation. S-boxes (non-trivial type) are essential and necessary elements of an effective cryptographic transformation, ensuring the operation of the nonlinear mixing of input data blocks bit segments.

Еще

Substitution, iterative cipher, the maximum differential probability, the maximum linear probability

Короткий адрес: https://sciup.org/15011123

IDR: 15011123

Текст научной статьи Importance of S-Blocks in Modern Block Ciphers

Published Online September 2012 in MECS DOI: 10.5815/ijcnis.2012.10.01

The most advanced conventional key cryptosystems are based on the idea of producing codes that represent a class of cryptosystems repeating a complex operation that transforms a plaintext in a cipher text. Each repetition (iteration) is known as a cipher cycle. The complex (composite) operation that is run in each cycle is usually a combination of a set of primitive operations, such as shift, a linear transformation, modular addition and substitution. In particular, the idea of Shannon is that a combination of permutation and substitution operations can lead to a cryptographically strong non-linear transformation, if a number of times is enough. Substitution operations in many ciphers appear at the same time as the main element of the cyclic nonlinear transformation (nonlinear element replacement). Therefore significant and even enormous efforts of researchers are focused on the study of approaches to the construction of permutations with high cryptographic performance. This branch of research is one of the most popular in modern cryptographic literature [1-13, and many others].

Nowadays the most developed mathematical apparatus for evaluation of cryptographic properties of nonlinear elements (S-blocks) is the methodology of linear algebra and, in particular, the apparatus of Boolean functions. Its development and application is the subject of many publications. There are some criteria and indicators to assess the properties of both the Boolean (component), S-block functions, and the properties of S-boxes in general such as: balance of Boolean function, nonlinearity N f , correlation immunity, propagation criteria (strict avalanche criterion) SAC ( k ), the algebraic degree of a Boolean function deg( f ) , as well as relevant characteristics of the S-boxes: a bit independence criteria (BIC), the criterion of non-linearity, maximum order of strict avalanche criterion (MOSAC), the maximum value of the linear approximation table (LAT), δ -smoothness (regularity) XOR-Table of S-box, and many others.

Running the Ukrainian contest for the nomination of candidates for the national standard of a block symmetric encryption as well as work on the analysis and examination of the proposed solutions have stepped up a new wave of interest in the study of properties and indicators of a number of proposed algorithms, including interest in the study and assessment of S-block designs used in construction of new codes.

It is important to emphasize that all known publications determine that mostly the S-boxes affect the performance stability of the cipher. There numerous papers [14-19, and more. etc.], devoted to the study of indicators of demonstrable strength of block symmetric ciphers, which are considered as maxima average differential and linear probabilities (MADP and MALHP) of multicycle transformations. These figures are expressed in terms of stability of the corresponding values of maximum differential and linear probabilities of the S-boxes used in ciphers.

At the same time, our recent works [20-24, etc.] based on the fact that stability of modern block symmetric ciphers to resist attacks of the linear and the differential cryptanalysis does not depend on S-boxes used (S-boxes of a non-trivial type). This provision is clearly contrary to the concept developed in the literature and therefore requires thorough and convincing evidence. In this work we pose a task of a more thorough and objective study of the significance of cryptographic S-boxes in modern block ciphers.

In the first part we give a brief overview of the theory and practice of substitutions in terms of cryptographic application. In the second part we describe the method of estimating cryptographic properties of S-boxes and propose a new approach to estimate the performance and ability of block symmetric ciphers to resist to attacks of linear and differential cryptanalysis. This analysis is not based on calculation of average values of the differential and linear probability maxima (MADP and MALHP) – it is based on calculation of average values of these probabilities maxima (AMDP and AMLHP). The third part represents results of the research on the role of substitution transformations in the iterative ciphers with weak and strong linear transformations. The results allow establishing independence of cipher durability to attack of linear and differential cryptanalysis from properties of S-boxes.

II. Brief Analysis of the Substitutions Research Results Regarding a Crytograchic

Application

We begin with a reference to the thesis [25] which is developed in KNURE and devoted to the methods of formation of random type S-block designs with improved cryptographic performance. In this paper we analyze in some detail a large number of publications in this area, so we just use the findings of the 2nd section of the dissertation, which brings us the following statements:

A. Existing approaches and the methods of constructing S-boxes are targeted primarily at ensuring the minimum values of the maxima of XOR differences DPmax tables and tables of linear approximations LPmax. Significant success has been achieved in this direction. We have implemented the S-block design with limit (theoretically lowest possible) values of the LPmax and DPmax parameters.
B. There is a thorough method for analyzing of the advanced cryptographic parameters (properties) of Boolean functions. Combining these methods we can describe the transformation of S-blocks. We have defined the approaches and rules by which the resulting cryptographic performance of individual Boolean functions in the S-box can be reevaluated in the performance of the transformation in general. Although a number of researches pay great attention to development and application of indicators to assess the cryptographic

S-boxes of the mathematical apparatus of Boolean functions, however, the algebraic approach which is used in the construction cipher S-boxes is not determinative. Moreover, S-boxes used in a number of modern ciphers are not the best ones and according to the number of indicators they possess very low cryptographic properties of the constituent Boolean functions.

C. The results represented here show that good S-boxes, as a rule, can be attributed to a number of random permutations, and, apparently, random checking can be included in the selection procedure for substitutions with good cryptographic properties, however, the evidences show that it is computationally very difficult to generate substitutions with high uniformity and with order 256 or more. That's why all the real development of the construction of large (byte) S-boxes is based on methods that can be named regular ones. For example, the paper [25] states that it is more progressive to use individual proposals that are available in publications, in particular, the proposal (reasons), K. Nyberg [26] for the construction of S-boxes. They found further development and practical application in the construction of S-boxes generated in the process of creating many new block symmetric ciphers (Rijndael, Labyrinth, ADE, etc.).

We have already noted in [20-24, etc.], which substantiates the position that the degree of resistance of modern block symmetric ciphers to attacks of linear cryptanalysis do not depend on differential properties of the S-boxes (except for the degenerate structures).

Most works in this direction are connected with the investigating of reduced to 16-bit input models of large ciphers, which usually uses 4-bit (input and output) S-blocks. It is the use of reduced models of ciphers became the basis for the proposed new approach (new ideology) to the assessment of resistance properties of iterative codes [24].

In the works mentioned above the cipher strength indicators are estimated using the average values of the differential and linear probabilities (AMDP and AMLHP), which are defined as follows (they are more adequate to the task of comparing with the MADP and MALHP, not to mention the benefits of computing):

Definition 1 (AMDP). The average value (over the set of 2 ^h keys) of the maximum differential probability of key-dependent function f [ k ]( x ) is h

ADMP^f = ave DP f [ k ^] = -1 V DP f [ k ^] (A x ^ A y ) f n max max .( )

^k ² k = 1

where 2 ^h is a power of a key set used for encryption

Definition 2 ( AMPLH ). The average value (over the set of 2 ^h keys) of the maximum linear probability of keydependent function f [ k ]( x ) is

1 ² ^h

AMLHP = aveLPf x(Гх ^ Гy) = — Y LPf [k] . (2) max max k 2 "k=i where 2h is a power of a key set used for encryption.

For more details regarding the definitions and notations see [14]. It is these figures that will be used in this work.

It is worth noting that the 4-bit S-boxes constructions are used while designing modern governmental block symmetric ciphers. It is suffice to mention at least a cipher Serpent, which took the second honored place in the competition AES.

It goes without saying that the study of cryptographic parameters of nibble S-boxes is a subject of many papers. We would like to bring your attention to two publications devoted to the study of nibble S-boxes that have appeared recently.

The publication [27] presents an exhaustive study of all 16! bijective 4-bit S-boxes. In the year 2007 Leander and Poschmann came up with the work presenting a complete picture of the affine equivalence classes. In their paper the authors present the results of further investigations of properties of optimal classes of S-block linear equivalence. In their analysis, they state that the two S-blocks are cryptographically equivalent, if they are isomorphic up to a permutation of the input and output bits and the XOR between input and output is a constant. In their paper the authors describe the list of such equivalence classes, with their differential and linear properties, and note that these classes are equivalent not only with differential and linear properties, but have equivalent algebraic properties: the number of branches and scheme complexity. The authors describe in their labor the "golden" set of S-boxes, which they believe have the perfect cryptographic properties.

In the second paper [28] authors describe quadratic approximation (of the Boolean functions) of a special form and the possibility to apply them in a non-linear cryptanalysis of block ciphers. It is shown that for the four-digit substitutions, which are recommended for using in the S-boxes algorithms GOST 28147-89, DES, and s3DES, that in almost all cases exist more probable (comparing to linear) quadratic relations of a special form for input and output bits of substitutions. It is noted that the majority of the considered S-boxes that are recommended for use in ciphers, there are linear equations exist with describing relation of ciphertext bits, which essentially can be used to solve systems of linear equations that arise in the analysis of ciphers. In this work, however, we are not interested in weakness of S-block designs, but rather in their cryptographic properties in general. In this respect, we can conclude that nibble S-boxes are explored more fully and deeply.

III. Methodology For Research

The attention of this paper is focused on the Nibble S-boxes used to construct the reduced code models. Here we depart from conventional approaches to assessing indicators of cryptographic S-boxes, and propose a new approach to determining the extent of their cryptographic suitability. This approach is based on estimating the number of cycles of transformation necessary for a cipher to achieve the stationary state, comparable with a random permutation of the corresponding degree. This steady state will be determined by the moment of reaching the minimum value of the maximum cipher table of XOR differences for the entire cipher (total differential) and the minimum value of the maximum displacement of the linear approximation table (LAT), which coincides, as shown by studies with a random permutation, which fits the bit entry size.

The focus will be on cipher models with 16-bit input and output. The moment when a cipher reaches the stationary state will be determined by the number of cycles when the average (among the keys) maximum value of the XOR-difference table is less than 20 (the theoretical maximum value of the differential tables of random permutations with degrees 216 equals 19.5 [29]). Steady-state value for the maximum displacement of the linear approximations table will be determined by the moment (the number of cycles) when measured maximum displacement of the linear approximations table is less than 900 (the theoretical value of maximum displacement of the linear approximations table of a random permutation with degree 216 equals to 750 [30], i.e. the experimental value will be a bit more than the theoretical value).

Let us explain the choice of such values.

Obviously, the empirical estimates of AMDP and AMLHP are random and not exactly equal to the values following from the theoretical distributions of random permutation (respectively 19.5 and 750).

How can we reasonably determine the time for cipher to reach a steady state?

The answer to this question can be obtained by using the method of confidence intervals, which is the method of mathematical statistics, specifically designed for constructing a set of approximate values of unknown parameters of probability distributions [31]. We have already described the essence of this approach in studying the avalanche properties of cipher GOST [33].

In accordance with the approach [32] described above, using the confidence level based on Student's distribution table [30] for given values and n = 30 (key size in our experiments), as well as the values of the dispersion distribution of differential XOR conversion table of random permutations in the form of the Poisson law [31]:

- 2

Рг[ Л ( А Х , A Y ) = 2 i ] » Poisson I i; -1 = e— ⁽³⁾

with parameter ^ = 1 , we get:

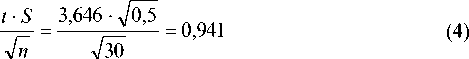
and, consequently, all values of the maxima of transitions between the input difference between and the output difference can be considered as matching the confidence interval, satisfying the following conditions:

19 - 0,941 < Л ( А Х , А У ) max < 19 + 0,941 .

In our experiments we will fix the getting into the confidence interval on the one hand in the form of inequality Л(А Х , А У )_max < 20 . While evaluating the properties of linear ciphers (reduced versions) we will take as basis the approximation of the law of displacements of linear approximations of the tables in the form of the normal law [33]:

Pr^( a , в ) = 2 x ] = Z (—x — 1 . (5)

I ₂( n - 4)/2 I

RMS value of this distribution law is equal to 2 ⁽ ⁿ ^4)/2 and for substitution with degree 2 ¹⁶ we have ²⁽16 ^- ^4)/2 = 2 6 . In this case, the algorithm for calculating tables of linear approximations is much slower (for the construction of the table we need to perform 2⁴⁸ operations). Therefore we will present experiments, performed for a single encryption key (and available results for a large number of keys). While determining the confidence interval in this case we will base on calculations performed for a sample of encryption using 10 keys. For the same values of the confidence level the value of the Student distribution table t equals to 4,587 , which leads to the result:

L S = 4,587 ^64 = ^

and, consequently, the confidence interval is determined by the boundary values:

750 - 93 < Л ( а , l )_max < 750 + 93 . (7)

These actual measurements for small codes, as we will see, will give higher average values of maximum displacement compared with the theoretical, so in this case we should take a one-sided boundary in the form of verification of comparatively overvalued inequality Л ( а , e ) max < 900 as a confidence interval.

It is important that these figures can be verified (estimated) basing on the use of small models, codes, use of which, as noted above, became the basis for implementing a new methodology for assessing the performance of demonstrable resistance of block symmetric ciphers [24]. We shall not repeat the results of the experiments with small models of different codes, which have already been shown many times.

Hereinafter we will consider two models (two types) ciphers. The first model will demonstrate (describe) a cipher with a weak linear transformation (avalanche factor equal to 3 in average), and the second - with a strong linear transformation (avalanche factor 5).

As a universal model of ciphers with weak linear transformation we will use 16-bit code, as proposed in the work of Professor Heys [34]. This is a cipher with substitution-permutation network structure (SPN), which is shown in Figure 1 (note that we count Feistel-like ciphers DES and GOST as the ciphers with weak linear transformation).

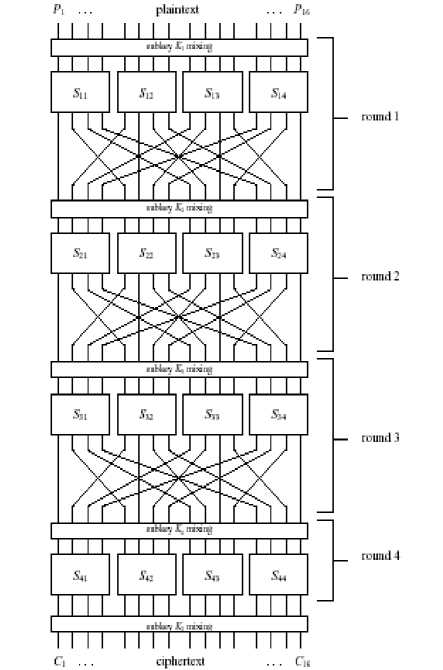
Figure 1.Sipher based on the substitution-permutation network (spn)

Operations performed in this cipher are largely similar to those used in the cipher DES. Many modern ciphers, including Rijndael are based on this scheme.

As we can see from the scheme of Figure 1, the input of the algorithm comes with 16-bit block of input text. This block is processed by repeating four cycles consisting of elementary operations: replacement, rearrangement and addition of bits with the key.

According to the algorithm in each cycle of the input 16-bit block of data is divided into four sub-blocks, each of which goes to the corresponding inputs block of replacement (S-units engaged in the replacement of four input bits for four output bits).

The linear transformation in each cycle carries a simple bits rearrangement of 4-bit output blocks of replacement (weak linear transformation). It is represented as a form of permutation, shown in Table I.

TABLE I. Permutation of the bits in the Heys cipher

Input	0	1	2	3	4	5	6	7	8	9	a	b	c	d	e	f
Output	0	4	8	с	1	5	9	d	2	6	a	e	3	7	b	f

To add a key (or a sub-key) the cipher uses a simple bit-operation of addition modulo 2 (XOR). In addition to cyclic sub-keys the algorithm processes an additional adding of key bits of the output bits of the previous cycle. This is traditionally done to complicate the encryption algorithm analysis. Sub-key for each cycle of transformation usually used in the encryption algorithms is extracted from the master key (master key). In all experiments, bits of sub-keys are generated independently and are not related to each other (although, as the experiments show, it does not matter).

As a cipher with a strong linear transformation we will take the reduced 16-bit input Rijndael cipher design. In this case, in all experiments with the cyclic transformations of the cipher four identical Nibble substitution (S-block) will be used, the outputs of which (set of four values of the output nibble of four S-boxes B = ( b 0 , b 1 , b 2 , b 3 )) will be processed with MixColumns operation using the entire text. The result of a linear transformation in this case is a 16-bit vector С = ( с 0 , с 1 , с 2 , с 3 ), determined using the matrix multiplication:

< 2 3 11 )

( с 0 , с 1 , с 2 , с 3 ) = ( b ₀, b 1 , b ₂, b₃ ) *

1 2 3

1 1 2 ,

The operation of matrix multiplication is performed in GF(24) field (the matrix elements are the elements of the GF(24) field). With this construction, the linear transformation operation ShiftRows is not required. Practically we can get the last construction from the Heys cipher replacing the linear transformation with a matrix transformation [35].

IV. Results And Interpretation

The first series of experiments was performed using the Heys cipher. The modifications we made in the original proposal [34] concluded that we have made the number of cyclic changes variable, and most importantly - we used in this cipher the substitutions of different types, taken from the above-mentioned works [27, 28].

Table II illustrates the results of experiments performed with the use of Heys cipher and substitutions from the list presented in [28]. It includes the substitution of the books, A.G. Rostovtsev and E.B. Mahovenko [36], which shows a series of extreme four-digit permutations S 1 ,...,S¹⁰, recommended for S-boxes of GOST 28147-89 standard (in Table II, these substitutions are serial numbers 1-10). It is noted that in each such substitution by multiplying it by affine substitution we can obtain a whole class of extreme permutations. They were chosen so as to maximize the cipher strength to the methods of linear and differential cryptanalysis.

TABLE II. Maxima values of total differentials (XOR tables) for the Hayes cipher for each cycle with different sets of S-boxes, taken from the work [28]

№	Substitutions from [29]	1	2	3	4	5	6	7	8	9	10
1	0,D,B,8,3,6,4,1,F,2,5,E,A,C,9,7	16384	4096	523,07	69,67	30,60	19,20	19,13	19,27	19,47	19,33
2	0,1,9,E,D,B,7,6,F,2,C,5,A,4,3,8	16384	4096	1828,80	383,73	114,53	32,93	20,40	19,60	18,87	19,13
3	0,1,D,B,9,E,6,7,C,5,8,3,F,2,4,A	16384	4096	1821,73	426,13	150,40	49,40	20,73	19,13	18,87	19,13
4	0,1,2,4,3,5,8,A,7,9,6,D,B,E,C,F	16384	4096	2671,47	1009,8	394,87	145,87	68,40	29,67	20,00	19,27
5	0,1,B,2,8,6,F,3,E,A,4,9,D,5,7,C	16384	4096	1172,87	351,67	112,33	42,80	21,20	18,80	19,27	19,33
6	0,1,B,2,8,3,F,6,E,A,4,9,D,5,7,C	16384	4096	2310,40	693,27	234,07	90,33	35,87	20,67	19,33	19,27
7	0,4,B,2,8,6,A,1,E,F,3,9,D,5,7,C	16384	4096	955,67	322,07	132,67	47,33	21,87	19,20	19,53	19,07
8	0,4,B,2,8,3,F,1,E,A,6,9,D,5,7,C	16384	4096	1495,47	397,40	126,47	46,40	21,87	18,73	19,20	18,87
9	0,B,F,9,1,5,6,8,3,A,4,C,E,D,7,2	16384	4096	1410,13	379,87	131,40	48,33	24,60	18,73	19,33	18,93
10	0,7,A,E,9,1,D,8,C,2,B,F,3,5,4,6	16384	4096	1985,87	686,33	186,33	61,80	23,73	19,20	19,20	19,40
11	4,A,9,2,D,8,0,E,6,B,1,C,7,F,5,3	16384	6144	2052,40	672,13	187,67	72,87	33,20	19,23	19,20	19,00
12	8,2,D,B,4,1,E,7,5,F,0,3,A,6,9,C	32768	9216	1298,33	328,53	68,47	29,80	19,53	19.13	19,07	18,87
13	A,5,3,F,C,9,0,6,1,2,8,4,B,E,7,D	32768	8192	1045,87	142,07	64,73	31,07	18,87	19,07	19,20	19,33
14	5,A,C,6,0,F,3,9,8,D,B,1,7,2,E,4	32768	16384	5043,20	1327,87	369,60	150,00	64,20	31,47	24,07	23,87
15	3,9,F,0,6,A,5,C,E,2,1,7,D,4,8,B	32768	8192	1338,67	184,67	43,73	19,87	19,47	19,33	18,00	19,00
16	F,0,A,9,3,5,4,E,8,B,1,7,6,C,D,2	32768	8192	2372,27	283,33	129,20	47,40	20,20	19,00	19,40	19,20
17	C,6,3,9,0,5,A,F,2,D,4,E,7,B,1,8	32768	8192	1716,80	258,33	85,60	35,80	19.07	1927	18,93	19,13
18	D,A,0,7,3,9,E,4,2,F,C,1,5,6,B,8	32768	16384	2080,00	415,47	117,80	42,53	18,93	19,07	19,33	19,33

Substitution S11 (with number 11 in Table II), as noted in [28], is taken from the book B. Schneier [37], which presents eight four-digit permutations, used in the encryption method in the application for the Standard Bank of Russia, as well as in the one-way hash function GOST.11-Standard.

The paper [28] describes 32 substitutions in the S-boxes of the modified algorithm s³DES [38], considered to be resistant to the methods of differential and linear cryptanalysis. It is noted that, among these, only seven substitutions (the substitutions S¹², _., S¹⁸) have nonlinearity NL = 4. They are presented in Table 2, with the numbers 12-18 accordingly.

As seen from the results for all variants involved in ciphers S-boxes (except the 14th) all ciphers for the first nine cycles of change have time to become random substitutions. We note here that the first eleven substitutions have values of 5 -uniformity (maximum value of the conversion of the XOR difference table) equal to the minimum possible value which equals 4, and the rest have a value of 5 - uniformity equal 8.Substitution at number 14 stands out by the differential performance from the overall list. It also came to the stationary state, but it turned out to be the asymptotic value of 24. Analysis has shown that this substitution apparently got into a list of [28] by mistake. According to our estimates it is related to the permutations of the degenerate type (has a value of nonlinearity parameter equal to zero).

Table III illustrates the results of experiments performed using a cipher described on the Figure 1 and substitution of [27] (substitution of the Serpent cipher and golden substitutions). There is a list of S-boxes from the other cipher is presented in the application of this work: Lucifer, Present, JH, ICEBERG, LUFFA, NOEKEON, HAMSI, Serpent, Hummingbird-1, Hummingbird-2, GOST and DES. However, we will use here S-blocks from cipher Serpent and golden substitutions. As can be seen from the results presented in the table, in this case, the substitutions from the Serpent cipher repeat the properties of the golden substitution [27] (which are the substitution of the same class).

TABLE III. Values of the XOR maxima for the Heys cipher for each cycle with different sets of S-boxes, taken from the work [27]

№	Substitution from the Serpent cipher	1	2	3	4	5	6	7	8	9	10
1	3,8,f,1,a,6,5,b,e,d,4,2,7,0,9,c	16384	4096	460,67	70,60	32,07	19,60	18,93	19,20	19,33	19,00
2	f,c,2,7,9,0,5,a,1,b,e,8,6,d,3,4	16384	4096	467,33	70,00	30,27	19,20	18,93	19,07	19,13	19,27
3	8,6,7,9,3,c,a,f,d,1,e,4,0,b,5,2	16384	4096	631,47	78,73	35,80	19,07	19,13	19,07	18,80	18,80
4	0,f,b,8,c,9,6,3,d,1,2,4,a,7,5,e	16384	4096	502,80	67,20	29,47	19,27	19,07	19,33	19,00	19,
5	1,f,8,3,c,0,b,6,2,5,4,a,9,e,7,d	16384	4096	446,93	70,87	30,40	18,80	19,07	19,13	18,80	19,20
6	f,5,2,b,4,a,9,c,0,3,e,8,d,6,7,1	16384	4096	437,60	82,40	32,33	19,07	19,20	18,87	19,20	18,80
7	7,2,c,5,8,4,6,b,e,9,1,f,d,3,a,0	16384	4096	514,13	66,27	26,00	18,80	19,40	19,07	19,13	19,27
8	1,d,f,0,e,8,2,b,7,4,c,a,9,3,5,6	16384	4096	454,00	64,73	29,07	19.07	19,20	19,00	18,80	19,20
	Golden substitutions	1	2	3	4	5	6	7	8	9	10
1	0,3,5,8,6,9,c,7,d,a,e,4,1,f,b,2	16384	4096	512,13	81,40	30,40	19,20	19,07	19,87	19,07	19,53
2	0,3,5,8,6,a,f,4,e,d,9,2,1,7,c,b	16384	4096	502,80	67,29	29,47	19,20	19,33	19,33	19,00	19,00
3	0,3,5,8,6,c,b,7,9,e,a,d,f,2,1,4	16384	4096	427,47	62,47	27,07	19,13	19,20	19,27	18,87	18,73
4	0,3,5,8,6,c,b,7,a,4,9,e,f,1,2,d	16384	4096	502,80	67,20	29,47	19,27	19,07	19,33	19.00	19,00

All substitutions in this experiment provide a transition to the random substitution properties within six cycles (is the smallest number of cycles for the output of the differential performance of the stationary state for the Heys cipher). Note that the limit values which came to the asymptotic value Λ ( Δ X , Δ Y )_max ≤ 20

demonstratesome of substitutions from the Table I, but overall rates substitution from Table II is much inferior to the dynamic characteristics of substitutions from Table III, i.e. they are not the best for the Heys cipher.

Tables IV and V show the results obtained for tables of linear approximations of the Heys cipher with the same S-boxes, as in the previous experiments (using a single decryption key). All substitutions listed in the tables, except for the substitution at number 14, have the maximum possible value of the nonlinearity parameter NL = 4. Here, the results presented in all cases (except the 14th substitution), confidently demonstrate the transition of ciphers with different structures S-boxes to the properties of a random permutation.

TABLE IV. Maxima values of linear approximation table for the Heys cipher for each cycle with different sets of S-boxes, taken from the work [28]

№	Substitutions from [29]	1	2	3	4	5	6	7	8
1	0,D,B,8,3,6,4,1,F,2,5,E,A,C,9,7	16384	1792	800	830	834	848	822	810
2	0,1,9,E,D,B,7,6,F,2,C,5,A,4,3,8	16384	2048	1280	830	834	810	798	860
3	0,1,D,B,9,E,6,7,C,5,8,3,F,2,4,A	16384	2048	848	798	796	824	800	822
4	0,1,2,4,3,5,8,A,7,9,6,D,B,E,C,F	16384	2048	832	878	820	876	788	830
5	0,1,B,2,8,6,F,3,E,A,4,9,D,5,7,C	16384	2048	832	796	800	820	786	814
6	0,1,B,2,8,3,F,6,E,A,4,9,D,5,7,C	16384	2048	816	810	848	792	800	792
7	0,4,B,2,8,6,A,1,E,F,3,9,D,5,7,C	16384	2048	816	800	816	800	846	786
8	0,4,B,2,8,3,F,1,E,A,6,9,D,5,7,C	16384	2048	816	814	832	804	838	820
9	0,B,F,9,1,5,6,8,3,A,4,C,E,D,7,2	16384	1664	848	792	824	816	870	822
10	0,7,A,E,9,1,D,8,C,2,B,F,3,5,4,6	16384	2048	808	818	824	840	824	804
11	4,A,9,2,D,8,0,E,6,B,1,C,7,F,5,3	16384	2048	848	830	798	790	848	790
12	8,2,D,B,4,1,E,7,5,F,0,3,A,6,9,C	32768	8192	2048	818	828	828	818	816
13	A,5,3,F,C,9,0,6,1,2,8,4,B,E,7,D	32768	8192	2048	844	818	858	786	824
14	5,A,C,6,0,F,3,9,8,D,B,1,7,2,E,4	32768	32768	32768	32768	32768	32768	32768	32768
15	3,9,F,0,6,A,5,C,E,2,1,7,D,4,8,B	32768	8192	1512	794	792	880	800	830
16	F,0,A,9,3,5,4,E,8,B,1,7,6,C,D,2	32768	8192	2048	824	826	818	846	826
17	C,6,3,9,0,5,A,F,2,D,4,E,7,B,1,8	32768	8192	1280	840	800	838	832	886
18	D,A,0,7,3,9,E,4,2,F,C,1,5,6,B,8	32768	8192	2048	796	836	816	812	830

Note that the substitution at number 14 and in this case indicates the practical unsuitability for the construction of encryption conversion. We will discuss in more detail the 14th, and the other weak substitutions later.

Further results are devoted to the analysis of differential and linear properties of the cipher (reduced models), when they use a strong linear transformation. Tables VI and VII present the results of evaluation of differential and linear indicators of reduced models of the Rijndael cipher with different structures S-boxes, repeating the previously discussed sets. In all cases, the baby-Rijndael ciphers implement noted above linear transformation MixColumns for the whole text (a strong linear transformation).

TABLE V. Maxima values of linear approximation table for the Heys cipher for each cycle with different sets of S-boxes, taken from the work [27]

№	Substitution from the Serpent cipher	1	2	3	4	5	6	7	8
1	3,8,f,1,a,6,5,b,e,d,4,2,7,0,9,c	16384	8192	4128	2032	1152	792	812	806
2	f,c,2,7,9,0,5,a,1,b,e,8,6,d,3,4	16384	8192	4352	2080	944	814	806	850
3	8,6,7,9,3,c,a,f,d,1,e,4,0,b,5,2	16384	8192	4128	2152	1154	844	822	808
4	0,f,b,8,c,9,6,3,d,1,2,4,a,7,5,e	16384	8192	4128	2032	888	796	800	818
5	1,f,8,3,c,0,b,6,2,5,4,a,9,e,7,d	16384	8192	4896	1892	942	882	830	858
6	f,5,2,b,4,a,9,c,0,3,e,8,d,6,7,1	16384	8192	4896	1712	1212	782	828	816
7	7,2,c,5,8,4,6,b,e,9,1,f,d,3,a,0	16384	8192	4896	1928	1112	812	842	868
8	1,d,f,0,e,8,2,b,7,4,c,a,9,3,5,6	16384	8192	3840	2064	956	818	812	830
	Golden substitutions	1	2	3	4	5	6	7	8
1	0,3,5,8,6,9,c,7,d,a,e,4,1,f,b,2	16384	8192	5056	1856	956	806	798	792
2	0,3,5,8,6,a,f,4,e,d,9,2,1,7,c,b	16384	8192	3936	1952	818	908	820	812
3	0,3,5,8,6,c,b,7,9,e,a,d,f,2,1,4	16384	8192	3648	1744	822	830	772	802
4	0,3,5,8,6,c,b,7,a,4,9,e,f,1,2,d	16384	8192	4128	2176	818	818	824	862

TABLE VI. Maxima values of total differentials (XOR tables) for the baby-Rijndael cipher for each cycle with different sets of S-boxes, taken from the works [27-28]

Substitutions from [27 - 29]		The number of encryption cycles
Substitutions from [27 - 29]		1	2	3	4	5	6
1	0,D,B,8,3,6,4,1,F,2,5,E,A,C,9,7	16384	128	19,33	19,13	19,53	19
2	0,1,9,E,D,B,7,6,F,2,C,5,A,4,3,8	16384	88	21,13	19,2	19,4	19
3	0,1,D,B,9,E,6,7,C,5,8,3,F,2,4,A	16384	128	19,67	19	19,67	19,33
4	0,1,2,4,3,5,8,A,7,9,6,D,B,E,C,F	16384	128	18,73	19	19,27	18,93
5	0,1,B,2,8,6,F,3,E,A,4,9,D,5,7,C	16384	128	19,13	18,73	19,2	19,13
6	0,1,B,2,8,3,F,6,E,A,4,9,D,5,7,C	16384	131,7	19,33	19,07	18,87	18,93
7	0,4,B,2,8,6,A,1,E,F,3,9,D,5,7,C	16384	80	19,2	19,13	19,33	18,87
8	0,4,B,2,8,3,F,1,E,A,6,9,D,5,7,C	16384	128	19,6	19,07	19,2	19,13
9	0,B,F,9,1,5,6,8,3,A,4,C,E,D,7,2	16384	128	19,2	19	19,4	19,4
10	0,7,A,E,9,1,D,8,C,2,B,F,3,5,4,6	16384	136	21,87	19,07	19,07	18,87
11	4,A,9,2,D,8,0,E,6,B,1,C,7,F,5,3	16384	222	20,13	19,67	19,2	19,47
12	8,2,D,B,4,1,E,7,5,F,0,3,A,6,9,C	24576	846	59,27	19,27	19,33	18,73
13	A,5,3,F,C,9,0,6,1,2,8,4,B,E,7,D	32768	1024	115,9	19,00	19,07	19,4
14	5,A,C,6,0,F,3,9,8,D,B,1,7,2,E,4	32768	2048	286	58,2	30,67	31
15	3,9,F,0,6,A,5,C,E,2,1,7,D,4,8,B	32768	576	42,6	19,13	19,13	19,2
16	F,0,A,9,3,5,4,E,8,B,1,7,6,C,D,2	32768	1024	120	19,07	18,73	19,13
17	C,6,3,9,0,5,A,F,2,D,4,E,7,B,1,8	32768	576	53,07	19,13	19,27	18,87
18	D,A,0,7,3,9,E,4,2,F,C,1,5,6,B,8	32768	768	80	19,07	19,07	19,47
Substitution from the Serpent cipher		1	2	3	4	5	6
1	3,8,F,1,A,6,5,B,E,D,4,2,7,0,9,C	16384	128	20,33	19,00	19,47	19,13
2	F,C,2,7,9,0,5,A,1,B,E,8,6,D,3,4	16384	96	19,07	19,07	19,67	19,33
3	8,6,7,9,3,C,A,F,D,1,E,4,0,B,5,2	16384	144	19,67	19,33	19,2	19,4
4	0,F,B,8,C,9,6,3,D,1,2,4,A,7,5,E	16384	96	19,8	19,27	19,13	19,13
5	1,F,8,3,C,0,B,6,2,5,4,A,9,E,7,D	16384	130,9	20,53	19,2	18,93	19,07
6	F,5,2,B,4,A,9,C,0,3,E,8,D,6,7,1	16384	130,1	19,27	19,13	19,2	19,13
7	7,2,C,5,8,4,6,B,E,9,1,F,D,3,A,0	16384	128	19,27	19	19,47	18,87
8	1,D,F,0,E,8,2,B,7,4,C,A,9,3,5,6	16384	128	22,2	18,93	18,73	18,8
Golden substitutions		1	2	3	4	5	6
1	0,3,5,8,6,9,C,7,D,A,E,4,1,F,B,2	16384	134,9	19,00	19,27	18,93	19,13
2	0,3,5,8,6,A,F,4,E,D,9,2,1,7,C,B	16384	128	19,80	19,00	1947	18,93
3	0,3,5,8,6,C,B,7,9,E,A,D,F,2,1,4	16384	128	19,53	19,2	19,27	19
4	0,3,5,8,6,C,B,7,A,4,9,E,F,1,2,D	16384	132	18,8	19,33	19,07	19,13

The presented results show that almost regardless of the structures of the used S-boxes, all the cipher variants for three or four cycles come to an asymptotic value of the maximum total differential, being equal to the theoretical value obtained for a random permutation [29].

A strong linear transformation almost smoothed the differences in the results

Finally, in the third series of experiments we estimate the differential and linear properties of the

TABLE VII. Maxima values of the linear approximation table for the baby-Rijndael cipher for each cycle with different sets of S-boxes, taken from the works [27-28]

Substitutions from [27 – 29] 1 2 3 4 5 6 7 1 0,D,B,8,3,6,4,1,F,2,5,E,A,C,9,7 16384 1792 800 830 834 848 822 2 0,1,9,E,D,B,7,6,F,2,C,5,A,4,3,8 16384 16384 1280 830 834 810 798 3 0,1,D,B,9,E,6,7,C,5,8,3,F,2,4,A 16384 2048 944 800 822 832 810 4 0,1,2,4,3,5,8,A,7,9,6,D,B,E,C,F 16384 2048 832 878 820 876 788 5 0,1,B,2,8,6,F,3,E,A,4,9,D,5,7,C 16384 2048 832 796 800 820 786 6 0,1,B,2,8,3,F,6,E,A,4,9,D,5,7,C 16384 2048 816 810 848 792 800 7 0,4,B,2,8,6,A,1,E,F,3,9,D,5,7,C 16384 2048 816 800 816 800 846 8 0,4,B,2,8,3,F,1,E,A,6,9,D,5,7,C 16384 2048 816 814 832 804 838 9 0,B,F,9,1,5,6,8,3,A,4,C,E,D,7,2 16384 1664 848 792 824 816 870 10 0,7,A,E,9,1,D,8,C,2,B,F,3,5,4,6 16384 2048 808 818 814 840 824 11 4,A,9,2,D,8,0,E,6,B,1,C,7,F,5,3 16384 2048 832 830 798 790 848 12 8,2,D,B,4,1,E,7,5,F,0,3,A,6,9,C 32768 8192 2048 822 840 798 882 13 A,5,3,F,C,9,0,6,1,2,8,4,B,E,7,D 32768 8192 2048 844 818 858 786 14 5,A,C,6,0,F,3,9,8,D,B,1,7,2,E,4 32768 32768 32768 32768 32768 32768 32768 15 3,9,F,0,6,A,5,C,E,2,1,7,D,4,8,B 32768 8192 1512 794 792 880 800 16 F,0,A,9,3,5,4,E,8,B,1,7,6,C,D,2 32768 8192 2048 824 826 818 846 17 C,6,3,9,0,5,A,F,2,D,4,E,7,B,1,8 32768 8192 1280 840 800 838 832 18 D,A,0,7,3,9,E,4,2,F,C,1,5,6,B,8 32768 8192 2048 796 836 816 812 Substitution from the Serpent cipher 1 2 3 4 5 6 7 1 3,8,F,1,A,6,5,B,E,D,4,2,7,0,9,C 16384 2048 872 878 808 862 844 2 F,C,2,7,9,0,5,A,1,B,E,8,6,D,3,4 16384 2048 816 792 786 882 874 3 8,6,7,9,3,C,A,F,D,1,E,4,0,B,5,2 16384 2048 880 820 816 844 860 4 0,F,B,8,C,9,6,3,D,1,2,4,A,7,5,E 16384 2048 800 844 856 844 850 5 1,F,8,3,C,0,B,6,2,5,4,A,9,E,7,D 16384 2048 840 864 838 798 778 6 F,5,2,B,4,A,9,C,0,3,E,8,D,6,7,1 16384 2048 808 846 820 822 832 7 7,2,C,5,8,4,6,B,E,9,1,F,D,3,A,0 16384 2048 808 866 830 826 828 8 1,D,F,0,E,8,2,B,7,4,C,A,9,3,5,6 16384 2048 872 820 826 792 804 Golden substitutions 1 0,3,5,8,6,9,C,7,D,A,E,4,1,F,B,2 16384 2048 800 814 844 786 806 2 0,3,5,8,6,A,F,4,E,D,9,2,1,7,C,B 16384 2048 824 794 804 868 836 3 0,3,5,8,6,C,B,7,9,E,A,D,F,2,1,4 16384 1792 808 812 846 782 822 4 0,3,5,8,6,C,B,7,A,4,9,E,F,1,2,D 16384 1792 864 824 786 794 826 cipher, using randomly generated substitutions. The results of these experiments are presented in Table VIII and Table IX (Table VIII illustrates the differential properties, and Table IX illustrates the linear properties).

According to the results from Table VIII and Table IX, we can conclude that the random S-boxes demonstrate the indicators that are just as good indicators of the previously discussed S-boxes (and perfect, too).

Note that the results from Table VIII obtained by averaging over 30 different keys, and for Table IX the results are obtained using a single key. The keys are generated randomly. It remains to note that these same results can be supported with the numerous other publications [23, 24 and etc.] which describe a new methodology for assessing the strength of block symmetric ciphers to attacks of differential and linear cryptanalysis.

The results of experiments performed in the present study showed that the properties (difference) of the substitutions can be felt (seen) only in ciphers with a bad

(ineffective) diffusion layer. Ciphers with good diffusion layer just do not feel the difference! The difference, if it exists, is shows itself in the number of cycles required for cipher to come to steady state. But the difference in the worst of cases reaches a maximum equal to three cycles.

In this stage we can note that the same conclusion we reached in the study of large codes.

Experiments with them also fully confirmed the initial hypothesis on the convergence of codes with the number of cycles to the properties of random substitution of the same degree [39, 40].

A few words about so-called degenerate substitutions. Experiments show that the degenerate substitutions should be attributed primarily to the substitution of nonlinearity parameters equal to zero (the maximum displacement of the LAT equal to 2 ⁿ ^- ¹). In Table X and Table XI we present the behavior of ciphers with such substitutions.

The examples are: identical substitution (the identity substitution of the symmetric group), recorded during experiments in Table I and Table III at number 14, and nonlinearity exponent equal to zero). We are concluding the specially generated substitution of [22] (with the this long discussion of the degenerate substitutions.

TABLE VIII. Maxima values of total differentials (XOR tables) for the baby-Rijndael cipher for each cycle with randomly generated S-boxes

Randomly generated S-boxes		1	2	3	4	5	6
1	0,A,4,C,3,7,E,9,1,F,2,B,5,6,D,8	24576	335,9	25,27	19,27	18,93	19,27
2	B,5,A,2,7,D,8,E,4,3,1,F,6,C,9,0	32768	768	34,4	19,07	18,87	19,27
3	3,B,4,C,1,A,8,5,2,0,D,E,7,6,9,F	24576	355,2	21,93	19	19,33	19,2
4	3,6,C,7,0,D,5,A,B,1,2,4,9,8,F,E	24576	223,2	19,53	19,2	19	18,93
5	2,4,5,A,9,E,7,B,C,6,F,3,1,0,8,D	24576	223,1	19,53	19,33	19,33	19,27
6	C,A,E,2,0,9,4,8,5,1,6,B,7,D,F,3	24576	524,00	32,13	19,33	19,27	19,00
7	0,D,F,5,7,4,3,B,E,6,9,2,8,C,1,A	24576	190,40	20,93	19,07	19,07	19,4
8	7,F,E,B,1,2,0,D,5,C,4,8,A,3,6,9	24576	328,00	35,6	19,33	19,13	19,2
9	4,2,0,E,6,B,D,7,C,A,9,F,1,5,3,8	24576	216	19,16	19,2	19,33	19,47
10	6,1,7,F,C,4,5,D,0,E,8,2,A,3,B,9	24576	336	29,07	19,2	19,53	19,27

TABLE IX. Maxima values of the linear approximation table for the baby-Rijndael cipher for each cycle with randomly generated S-boxes

Randomly generated S-boxes		1	2	3	4	5	6
1	0,A,4,C,3,7,E,9,1,F,2,B,5,6,D,8	24576	5184	1000	796	814	824
2	B,5,A,2,7,D,8,E,4,3,1,F,6,C,9,0	24576	5248	1616	828	838	836
3	3,B,4,C,1,A,8,5,2,0,D,E,7,6,9,F	24576	3584	984	816	808	794
4	3,6,C,7,0,D,5,A,B,1,2,4,9,8,F,E	24576	3584	816	794	820	808
5	2,4,5,A,9,E,7,B,C,6,F,3,1,0,8,D	24576	3520	856	886	844	866
6	C,A,E,2,0,9,4,8,5,1,6,B,7,D,F,3	24576	5248	1096	826	804	822
7	0,D,F,5,7,4,3,B,E,6,9,2,8,C,1,A	24576	3584	928	858	816	810
8	7,F,E,B,1,2,0,D,5,C,4,8,A,3,6,9	24576	3520	808	874	850	842
9	4,2,0,E,6,B,D,7,C,A,9,F,1,5,3,8	16384	2048	816	800	784	880
10	6,1,7,F,C,4,5,D,0,E,8,2,A,3,B,9	24576	5248	1576	900	814	850

TABLE X. Maxima values of XOR table for the Heys cipher for each cycle with the degenerateS-boxes

	Substitution	Maxima value for XOR table for the different cycle numbers
1	1,2,3,4,5,6,7,8,9,1A,B,C,D,E,F LAT – 8, XOR – 10	1	2	3	4	5	6
		57617,07	50364,40	45675,60	40971,40	37338,80	39267,00
		Number of cycles
		7	8	9	10	11	12
		41487,80	43386,53	44803,13	46411,40	47075,40	47872,93
	Substitution 14 from Table 2	Number of cycles
2	5,A,C,6,0,F,3,9,8,D,B,1,7,2,E,4 LAT – 8, XOR – 8	1	2	3	4	5	6
		32768	16384	5043,20	1327,87	369,60	151,07
		Number of cycles
		7	8	9	10	11	12
		61,53	32,60	24,20	23,87	23,93	24,13
	Substitution 1 from Table 9	Number of cycles
3	C,D,5,1,A,B,6,2,E,3,7,F,4,0,8,9 LAT – 8, XOR – 12	1	2	3	4	5	6
		49152,00	27648,00	15552,00	3616,00	1016,00	451,27
		Number of cycles
		7	8	9	10	11	12
		209,27	106,60	53,07	27,53	20,07	19,07

It is important to highlight that the probability of being in a degenerate substitution during their random formation is very low. Thus, the probability of getting a nibble substitution nonlinearity exponent equal to zero, according to calculations, is close to 0.0001. To generate the byte substitution with the same exponent of nonlinearity we will need to iterate over one billion permutations.

However, the examples of degenerate and nondegenerate permutations clearly indicate that the S-boxes in the ciphers are very important. It is impossible to build good cryptographic transformations without substitutions non-degenerate type. Substitutions work one of the important mechanisms for cipher - the mechanism of nonlinear mixing (rearrangement) bits of data blocks by means of which the effect of randomness in their transformation is possible most easily to achieve.

TABLE XI. Maxima values of the linear approximation table for the Heys cipher for each cycle with the degenerate S-boxes

	Substitution	Maxima value for LAT table for the different cycle numbers
1	0,1,2,3,4,5,6,7,8,9,1A,B,C,D,E,F	1	2	3	4	5	6
		32768	32768	32768	32768	32768	32768
		Number of cycles
		7	8	9	10	11	12
		32768	32768	32768	32768	32768	32768
	Substitution 14 from Table 2	Number of cycles
2	5,A,C,6,0,F,3,9,8,D,B,1,7,2,E,4	1	2	3	4	5	6
		32768	32768	32768	32768	32768	32768
		Number of cycles
		7	8	9	10	11	12
		32768	32768	32768	32768	32768	32768
	Substitution 1 from Table 9	Number of cycles
3	C,D,5,1,A,B,6,2,E,3,7,F,4,0,8,9	1	2	3	4	5	6
		32768	24576	12288	5244	2044	1080
		Number of cycles
		7	8	9	10	11	12
		792	872	826	816	842	816

VI. Conclusions

There are quite a lot of well-known S-box structures, designed and used in a variety of ciphers (S-boxes that are built using the apparatus of Boolean functions, S-boxes, constructed on the basis of a deterministic type of transformation, random permutations, constructed using different criteria, S-boxes selected by exhaustive search according to certain criteria, and other structures). As we can see from the results, you can see the difference between the S-blocks only when used in a cyclic transformation of a cipher with a weak linear transformation (like in DES or Heys ciphers). This weakness shows itself in the increased number of cycles of encryption required to achieve steady-state, which is defined as the time from which the laws of XOR table distribution and table of linear approximations begin to repeat the relevant laws of probability distribution of a random permutation. Next, we present an analysis of the dynamic properties of the Heys cipher for Nibble S-boxes (cipher with a weak linear transformation), which are concentrated around the following statements:

• the most effective S-boxes, called ideal in the [28]. For them, the minimum number of cycles required for the Heys cipher to achieve a steady state with differential parameters is equal to 6 (for linear parameter it is even 5);
• all the other S-boxes of a special type from [28 and others], as well as the S-boxes of deterministic and random type have a dynamic performance of coming to a steady state, varied considerably (from 6 to 9 or more cycles);
• S-boxes, which were used while design modern ciphers, aimed at ensuring the minimum of values of delta-uniformity and the maximum attainable values of the nonlinearity (S-boxes constructed by the ideas of K. Nyberg: S-block of AES, Camellia, Labyrinth, ADE, etc.), in terms of dynamic properties have quite low performance;

Good linear transformation (a transformation with a high branching factor) eliminates the difference between the S-boxes (of a non-trivial type). All known S-boxes used in the ciphers, show almost the same value performance indicator (the number of cycles to achieve a steady state output equal to 3-4).

In general, if we talk about the asymptotic values of the maxima of the differentials and linear hulls (calculated with the full set of enciphering conversions) determining stability performance by modern standards, then for almost all known ciphers, they (values) do not depend on the properties of S-blocks used. This fact leads to an important conclusion for cryptography that seeking S-block constructions with improved cryptographic performance is not a prospective task and it is the intensively developing direction of cryptography has no future. To be more precise, those are cipher with a strong linear transformation. For a cipher with an inefficient linear transformation the problem of finding better S-block structures remains relevant, but we must accept the fact that the cipher with an inefficient linear transformation will always be significantly (three or more cycles) worse in terms of dynamics of the transition to the stationary state required for a cipher with a strong cipher a linear transformation. Moreover, for the cipher with an inefficient linear transformation the S-blocks may be such that the cipher will have an overextended period of transition to the stationary state, as it turned out, for example, for cipher DES when it took 13 cycles to obtain differential characteristic significantly more plausible than it follows from theoretical calculations for the random substitution.

At the same time, the S-blocks are necessary and essential part of effective encryption with the main importance being one of the main functions of encryption procedures - a nonlinear entanglement of bit outputs, with the main importance is the property of chaotic nonlinear conversion, which is shown mostly in a random change of bit positions in its output. When we deal with sequential execution of several of these conversions is practically independent regardless the specific type of the initial non-linear conversion (of a non-trivial type) we face a statistical balancing of effects from the impacts of each of the input bits, which results in a homogeneous (stationary) distribution for each transition of the input difference ∆X in the output difference ∆Y.

The blocks of nonlinear substitutions (S-blocks) only affect the dynamics of the transition to stationary states, attributable of random permutations of a corresponding degree. Thus, S-blocks are an essential component of modern iterative ciphers. This is one of the simplest mechanisms of introduction of non-linearity in the cryptographic transformation, although implementing a nonlinear transformation is possible without the S-block designs (such as in the code ThreeFish). But in this case, the non-linear transformation can be interpreted as the corresponding S-box. Removal of non-linear transformation (or its low efficiency) destroys one of the essential mechanisms of random mixing implemented by a cipher.

It should be noted that the nonlinear substitution transformations play an important role in the formation of mechanism of random mixing. They (S-blocks) are themselves a source of random permutations of bits of input data blocks. And without the introduction of random component, set by the cyclic sub-keys , the product of substitution transformation leads to the random resulting substitutive transformation (the distribution laws of transitions XOR tables and the tables shifting of linear approximations repeat the corresponding laws of distributions of random permutation), regardless of the initial permutation conversion (not trivial type). Dew to this mechanism (it can be said of the law of nature) a cycle reaches the steady state which involves increasing a number of cycles. Further increase in a number of cycles does not make in impact on the cipher performance durability.

Another fact revealed during the experiments: a good substitutions including ideal ones are not devoid of identical transitions (fixed points). Moreover substitutions, with up to 6 fixed points (in our experiments) are more suitable for cryptographic applications.

No doubt that similar conclusion will be true for higher degree substitutions.

Список литературы Importance of S-Blocks in Modern Block Ciphers

С. М. Adams. A formal and practical design procedure for Substitution-Permutation network cryptosystem. PhD thesis, Department of Electrical Engineering, Queen's University at Kingston, 1990.
С. M. Adams. And S.E. Tavares. The Structured design of cryptographically good S-boxes. Journal of Cryptology, 3(1): 27-41, 1990.
R. Forré. Methods and instruments for designing S-boxes. Journal of Cryptology, 2(3): 115-130,1990.
K. Nyberg. Perfect nonlinear S-boxes. In Advances in cryptology - EUROCRYPT91, volume 547, Lecture Notes in Computer Science, pp. 378-386. Springer-Verlag, Berlin, Heidelberg, New York, 1991.
E.F. Brickell, J.H. Moore, and M.R. Purtill. Structure in the S-boxes DES. Advances in cryptology, CRYPTOZb, Lecture Notes in Computer Science, vol. 263.A.M. Odlyzko ed., Springer-Verlag, pages 3-8, 1987.
M. H. Dawson. A unified framework for substitution box design based on information theory. Vaster's thesis, Queen's University, Kingston, Ontario, Canada, 1991.
E. Biham, A. Shamir. Differential Cryptanalysis of DES-like Cryptosystems. Journal of Cryptology, Vol. 4 No.l, 1991, pp. 3-72.
K. Nyberg and L.R. Knudsen. Provable security against differential cryptanalysis. In Advances in cryptology - EUROCRYPT'92, volume Lecture Notes in Computer Science, Springer-Verlag, Berlin, Heidelberg, New York, 1992, pp. 566-574.
T. Beth and C. Ding. On permutations against differential cryptanalysis. In Advances in cryptology - EUROCRYPT'93. Springer-Verlag, Berlin, Heidelberg, New York, 1993.
K. Nyberg. Differentially uniform mappings for cryptography. In Advances in cryptology - Proceedings of EUROCRYPT'93 (1994) vol. 765, Lecture Notes in Computer Science Springer-Verlag, Berlin, Heidelberg, New York, pp. 55-65.
Seberry J., Zhang X.M., Zheng Y.: Relationships among nonlinearity criteria. Presented at EUROCRYPTV4, 1994.
F. Sano, K. Ohkuma, H. Shimizu, S. Kawamura. On the Security of Nested SPN Cipher against the Differential and Linear Cryptanalysis/ IEICE Trans. Fundamentals, vol. E86-a, NO.1 January 2003, pp. 37-46.
S. Hong, S. Lee, J. Lim, J. Sung, D. Cheon and I. Cho. Provable Security against Differential and Linear cryptanalysis for SPN Structure. B. Schneier (Ed.): FSE 2000, LNCS 1978, pp. 273-283, 2001.
L. Keliher, H. Meijer, and S. Tavares, "New method for upper bounding the maximum average linear hull probability for SPNs," Advances in Cryptology, Proceedings of Eurocrypt '01, LNCS 2045, B. Pfitzmann, Ed., Springer-Verlag, 2001, pp. 420-436.
L. Keliher, H. Meijer, and S. Tavares, "Improving the upper bound on the maximum average linear hull probability for Rijndael", Advances in Cryptology, Selected Areas in Cryptography '01, LNCS 2259, S. Vaudenay, A.M. Youssef, Eds., Springer-Verlag, 2001, pp. 112-128.
Thomas Baignoires and Serge Vaudenay. Proving the Security of AES Substitution-Permutation Network. http://lasecwww.epfl.ch. 2004. p. 16.
Aleksiychuk A.N. Assessing the stability of a block cipher Kalina on the methods of the difference, with respect to linear cryptanalysis and algebraic attacks based on homomorphisms. / A.N. Aleksiychuk, L.V. Kovalchuk, E.V. Skrypnyk, A.S. Shevtsov // Applied electronics. 2008. vol.7. № 3. pp. 203-209.
Lisitskaya I.V. On Participation of S-boxes in the formation of maximum differential probability of block symmetric ciphers. / I.V. Lisitskaya, A.V. Kazimirov // Proceedings International Conference SAIT 2011, Kyiv, Ukraine, May 23-28. – 2011, p. 459.
Kuznetsov A.A. Linear properties of block symmetric ciphers submitted to the Ukrainian competition. / A.A. Kuznetsov, I.V. Lisitskaya, S.А. Isaev, Applied electronics, 2011. Vol.10, № 2, pp. 135-140.
Lisitskaya I.V. Participation of S-boxes in the formation of maximum linear probability of block symmetric ciphers. / I.V. Lisitskaya, V.V. Kovtyn //Radio Technical Collection 2011. no. 166, pp. 17-25.
Lisitskaya I.V. A new assessment of the ideology of resistance block symmetric ciphers to attacks of the differential and linear cryptanalysis, Krasnoyarsk, 2011. Proceedings of the 1st All-Russian scientific and practical forum of young scientists and specialists "Modern Russian science through the eyes of young researchers", Krasnoyarsk, 2011, pp. 18-120.
Lisitskaya I.V. Methodology for assessing stability of block symmetric ciphers, Automated control systems and automation devices, 2011, № 163, pp. 123-133.
Alexey Shirokov. Methods of formation of S-type random block designs with improved cryptographic performance (for block symmetric ciphers with provable security): Thesis. 05.13.21. Shirokov Alexey, Kharkov, 2010. 265. Bibliography, pp. 215-232.
K. Nyberg Differentially uniform mappings for cryptography. In Advances in cryptology - Proceedings of EUROCRYPT93 (1994) vol. 765, Lecture Notes in Computer Science Springer-Verlag, Berlin, Heidelberg, New York, pp. 55-65.
Markku-Juhani O. Saarinen Cryptographic Analysis of All 4×4-Bit S-Boxes. IACR Cryptology ePrint Archive Vol. 2011 (2011), p. 218.
N. Tokareva Quadratic approximation of a special form for the four substitutions in the S-boxes, Applied discrete mathematics, 2008. Vol. 1, № 1, pp. 50-54.
Oleynikov R.V., Oleshko O.I., Lisitsky K.E., Tevyashev A.D. Differential properties of substitutions, Applied electronics, 2010. Vol.9, Number 3, pp. 326-333.
V. Dolgov Properties of linear approximation tables of random permutations, Applied electronics, Kharkov: KNURE. - 2010. Vol. 9, № 3, pp. 334-340.
Lisitskaya I.V. Comparative analysis of the mechanisms of avalanche effect in the DES algorithm and GOST 28147-89, Іnformatsіyno-keruyuchi systemy na zalіznichnomu transportі, № 3. pp.24-30.
Joan Daemen, Vincent Rijmen Probability distributions of Correlation and Differentials in Block Ciphers. / Joan Daemen, Vincent Rijmen, April 13, 2006, pp. 1-38.
H. M. Heys. A Tutorial on Linear and Differential Cryptanalysis, CRYPTOLOGIA, v 26, N 3, 2002, p 189-221.
Dolgov V.I. Variations on the theme of the cipher Rijndael, / V.I. Dolgov, I.V. Lisitskaya, A.V. Kazimirov // Applied electronics 2010, Vol.9, № 3, pp. 321-325.
Rostovtsev A., Introduction to the theory of iterated, St. Petersburg: NGO Peace and the Family, 2003.
Schneier B. Applied Cryptography. Protocols, algorithms, source code in C, Moscow: Triumph, 2002.
Kim K., Park S., Lee S. Reconstruction of s2DES S-Boxes and their Immunity to Differential Cryptanalysis // Korea - Japan Workshop on Information Security and Cryptography. (Seoul, Korea. October 24–26, 1993) Proc., pp. 282-291.
Lisitskaya I.V. The large ciphers - random substitution, Interdepartmental Scientific. Radio Technical Collection, 2011, no. 166, pp. 50-55.
Lisitskaya I.V. Differential properties of the cipher FOX. / I.V. Lisitskaya, D.S. Kaidalov // Applied electronics, 2011, Vol.10, № 2. pp. 122-126.

Еще

Статья научная