Improved Cryptanalysis of CMC Chaotic Image Encryption Scheme

Published Online December 2010 in MECS

Because of the chaotic map’s random behavior and sensitivity to initial conditions and parameter settings, Some researchers have pointed out that there exists tight relationship between chaos and cryptography [1–7]. Many fundamental characteristics of chaos, such as the ergodicity, mixing and exactness property and the sensitivity to initial conditions, can be connected with the “confusion” and “diffusion” property in cryptography. So it is a natural idea to use chaos to enrich the design of new ciphers.

Chaos-based encryption is not a very new idea. In 1989, Matthews [8] used chaotic dynamical systems in cryptography firstly. He derived a one-dimension chaotic map, which is used to generate a sequence of pseudorandom numbers. Then, Fridrich proposed another encryption algorithm based on two-dimensional chaotic systems is in [9]. After that the map is extended to three dimensions to obtain a more complicated substitution cipher that can be used for the purpose of image encryption. In [1], a new image encryption algorithm based on chaotic map has been proposed. The main ideal of the image encryption algorithm is that Chen et al extending the traditional two-dimensional Cat mapping to three-dimensional generalized Cat mapping. Additionally, based on this the chaotic mapping, they designed a symmetric image encryption algorithm (denoted as CMC). In the algorithm, the domain of the three-dimensional generalized Cat mapping is limited in the remain class ring of the three-dimensional space. However, the strict mathematical chaotic transformation is defined in the real

fields. We noticed that the designer ignored this weakness, and based on this, we can attack on the CMC chaotic image encryption algorithm with known image.

In [10], Guo analyzed the security of Chen’s image encryption algorithm when the round function iterates only one time, and the case that the algorithm iterates more than one times is not analyzed. Additionally, the proposed solution algorithm did not use the characteristics of gray transformation. To the best of our knowledge there is no security analysis of this image encryption algorithm. Therefore, the aim of this paper is to assess the security of such cryptosystem, and we study the security with known image of CMC chaotic image encryption scheme, give an attack algorithm of equivalent key, and analyze the concrete computation complex of proposed attack algorithm. The result shows CMC algorithm is not secure with known image.

The rest of the paper is organized as follows. Section II describes the cryptosystem introduced in [1]. After that, Section III points out some design problems inherent to that cryptosystem, and Section IV gives some attacks on the cryptosystem under study. Then, section V presents the efficient of the attacking algorithm. Finally, Section VI concludes the paper.

II. DESCRIPTION OF THE ENCRYPTION SCHEME

The traditional two-dimensional Cat map is now generalized to three-dimensional Cat map by introducing Arnold transformation. The extended Cat map is a threedimensional invertible chaotic map described by

f : Z n x Z n x Z n a Z n x Z n x Z n

fv A xn +1

y„ + 1

a

' xn ' a y„

mod N

V zn + i 7      V zn 7

where

A =

1 + a x a z b y b z ⁺ a x b y ⁺ a x a z b y b z a x b x b y ⁺ b y

az              ay + axaz + axayazby azbz +1 ayaz + axayazbybz + axazaz + axayaz + ax bx           axaybxby + axbx + ayby +1

and a_x , b_x , a_y , b_y , a_z , b_z are all positive integers.

Based on the generalized Cat map, the complete image encryption scheme consists of five steps of operations, as shown in Fig. 3.

Step1 Pile up the two-dimensional image into threedimensional. Suppose that the image to be encrypted is of W -pixel length and H-pixel wide, in totally W x H . First, one needs to pile up all pixels of the image, to form several cubes of size N 1 x N ₁ x N ₁ , N 2 x N 2 x N 2 , ..., N i x N i x N i , respectively. To convert an image into several cubes, the following condition must be satisfied:

W x H = N 13 + N 23 + L + N 3 + R where N i e { 2,3,K, N } is the side length of each cube. N is the size of the maximum allowable cube, and R e { 0,1,2,K ,7 } is the remainder.

Step2 Perform the three-dimensional Cat map. Use a _x , b _x , a _y , b _y , a _z , b _z as control parameters to perform the three-dimensional discrete Cat map on each image cubes, generating shuffled images.

Step3. Diffusion process. Set C (0) = S , then perform the diffusion process once according to the algorithm described as follow.

C ( k ) = ф ( k ) © { [ I ( k ) + ф ( k ) ] mod M } © C ( K -1) where I ( k ) is the currently operated pixel and C ( k - 1) is the previously output cipher pixel. M is the color level (for a 256 grey-scale image, M=256). Set the initial value x (0) = L i . Computer the chaotic Logistic map:

x ( k + 1) = 4 x ( k )[1 - x ( k )]

If the next value obtained is within the subinterval (0.2, 0.8), then digitize it by amplifying it with a proper scaling and sampling, and obtained the valued ф ( k ) ; otherwise, the iteration goes on until a desired number in (0.2, 0.8) is obtained.

Step4 . Transform the three-dimensional cubes back to a two-dimensional image. The three-dimensional cubes are appropriately arranged, laying back to a twodimensional image for display or for storage.

Step5 . Key generation. The image encryption scheme uses the chaotic system as follow:

• ^x = a ⁽ y ^- x )

•

• < y = ( c - a ) x - xz + cy                  (2)

• z = xy - bz where a,    b,    c are parameters. When a = 35,b = 3,c e [20,28.4], the system is chaotic. The key used in the proposed encryption scheme is a binary sequence of 128 bits. The binary sequence is divided into eight segments, denoted as k ,k ,k ,k ,k ,k ,k ,k , ax x ay y az z         s respectively, each with 16-bit long. Parameters k ,k ,k ,k ,k ,k are used to generate the six control ax bx ay by az bz parameters of the extended three- dimensional Cat map (1), while kl and ks are used to generate the initial two values Li , S of Step 4.

In detail, to generate a x and b x , the following formulas are first used to compute the control parameter c of Chen’s system:

c = K x 8.4 + 20 a _x

E 15

K (i) x 2 i, K (i) is the i-th bit in i=0 ax                     ax sequence Kax . Initial values x0 ,y0 ,z0 are also derived from Kax and Kbx , by using the following formulas:

x ₀ = K bx x 80 - 40 , y 0 = K a, x 80 - 40, ^z 0 = K b, ^{x 60} .

Then, in the next step, parameters are set as a = 35, b = 3 , and the other parameters obtained above of (2) are used to iterate (2) for 100 and 200 times, respectively, yielding two values: ( x ₁₀₀, y ₁₀₀, z ₁₀₀) and ( x ₂₀₀, y ₂₀₀, z ₂₀₀). Next, then, the following formulas are used instead, to generate the final parameter values of a x and b x .

a _x = round ( ^{z 1} 0/' 6'0 x N ), b _x = round ( ^{z 20} ° 6Q x N ).

where N is the side length of cube to be scrambled by the 3D cat map.

A similar process is performed to obtain the control parameters a _y , b _z , a _z , b _y , and the initial values of the Logistic map L i , and the initial value of the mod operation, S . The following two formulas are used instead, to generate L i and S :

• 7  /

^z 100

L i = /60

S = round ( ^{z 2} 0/^, б0 x 255)

The complete image encryption scheme shows in Figure. 1.

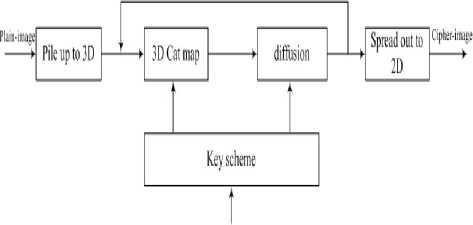
Figure. 1. Block diagram of the image encryption

• III.    THE ANALYSIS OF CHAOTIC IMAGE ENCRYPTION ALGORITHM

Chen et al extended the traditional two-dimension Cat mapping to three-dimensional generalized Cat mapping in [1], and using the extended mapping, designed an image encryption algorithm. The algorithm consists of five parts, limited to the article length, specific processes and symbolic description see [1] and [10].

Firstly, we analyze the three-dimensional generalized Cat mapping used in the image encryption scheme. In the image encryption scheme, the three-dimensional generalized Cat mapping A is 3-order degree matrix which defined in Z (N) , where N is the allowed

maximum length side of cube in the step 2. Set

[ a ll

a 12    a 13 )

B = A =

^a 21

^a 22

^a 23

mod N

V a 31

a 32    a 33 ;

Obviously, if we compute the value of B , that is to say we get the a j (1 <  i , j <  3) in the domain Z(NN ) , we can

easily obtain the image pixel transformation’s equivalent key.

Theorem 1[10] Suppose w(i,j,k)+ w(l,m,n) is the linear combination of the pixel positions (i, j,k) and

( l , m , n ) , and after the step 2 transformation, set the coordinate pixel positions are ( x , y , z ') and ( x ", y",z ’) , then

( x ”, y ”, z ”) = w ( x , y , z ) + w ' ( x ', y ', z ' ) mod N

In particular, if one of w and w' is 0, let w' = 0 , then

(x ”, y”, z”) = w (x, y, z) mod N

Theorem 2 ^[11] If N >  1 , set

A= imq + Ipk + jno - omk - pnk - Ijq , ( A , N ) = 1, then the pair of congruent polynomial equation

\ir + js + kt = e (mod N)

Ur + ms + nt = g (mod N)

[ or + ps + qt = f (mod N)

has a unique solution in Z ( N )

r = A^-1 ( emq + gpk + jnf - fmk - pne - gjq ) (mod N )

( s = A^-1 ( igq + lfk + eno - ogk - fni - leq )       (mod N )

t = A^-1 ( imf + lpe + jgo - ome - pgi - ljf )     (mod N )

where A ‘ A= 1 ( mod N ) .

The three-dimensional generalized Cat mapping A as a part of the algorithm is reversible transformation. According to theorem 2, as long as we know three pixels’ positions ( i , j , k ) , ( l , m , n ) , ( o , p , q ) which content the equation

( imq + lpk + jno - omk - pnk - ljq, N) = 1

The corresponding pixels’ positions after the pixel transformation are ( x , y , z ) , ( x ' , y ' , z ') , ( x",y",z ") , then we can obtain the unique equivalent key of the pixel transformation.

IV. THE EQUIVALENT KEY ATTACK ALGORITHM OF CMC

Define 1 If the adversary except knew the image encryption algorithm, but also obtained a pair of image information (plain-image and the corresponding cipherimage using the identical key), we called this condition is attack with image known.

We attack the image encryption algorithm under the condition that we know the plain-image and the corresponding cipher-image. Firstly, we attack the kind of algorithm that step2 and step 3 only iterate only one time. According to the key schedule of the cipher, the key parameters L_i , S are related with k_l , k_s . Therefore, we can first transform the known two-dimension image into

three-dimensional image, then exhaust the values k_l , k_s and use the key generation algorithm to generate L_i , S , using inverse transformation of step 3

I ( k ) = {фk ) ® C ( k ) ® C ( k -1) + M - ф ( k )} mod M Then, decrypt the three-dimensional cipher-image, denoted the decryption image as three-dimensional chaotic cipher-image. By the encryption algorithm, the three-dimensional chaotic cipher-image is the threedimensional plain-image after the three-dimensional generalized Cat transformation.

Compute the greatest common factor d of N , and exhaust the position values of three-dimensional image pixel transformation. In particular, the position value (0,0, d ) after the step 2 transformation would have the least results. Let the transformation result is ( e , f , g ) . Because of the three-dimensional generalized Cat transformation only changes the position of the image pixels and not changes the value of the image pixels. So, the position pixel ( e , f , g ) can only select the cipherimage pixel that has the same gray value with (0,0, d ) in the plain-image.

According to theorem 1, after transformation, the corresponding image positions of (0,0, wd )( w = 2,3,L) are ( e , f , g ) and ( we (mod N ), wf (mod N ), wg (mod N )) . Thus the two pixel positions (0,0, d ) and (0,0, wd ) would be changed          to          be           ( e , f , g )           ,

(we(modN), wf (modN), wg(modN)) . Meanwhile, we can compute the gray values of the four pixel positions in the three-dimensional plain-image and cipher-image, denoted as g (0,0, d)    , g (0,0, wd)    , g'(e, f, g) and g'( we (mod N), wf (mod N), wg (mod N)) . As the threedimensional generalized Cat mapping transformation only change the pixel gray position and does not change the gray value, then to verify the equation

g (0,0, wd ) = g '( we (mod N ), wf (mod N ), wg (mod N ))

This condition can be used to verify the exhaustive values of k_l and k_s , further more it also test whether the supposition ( e , f , g ) is correct or not. Set the count of the position (0,0, d ) that in the three-dimensional chaotic cipher-image and plain-image has the same gray value is M s . A wrong supposition through the above test’s probability approximate is у M's , so take the number of w is T , and by T times the corresponding probability is (1/M s ) T . After the transformation, the number of the supposition position is M’ , so take T >  1 , and make the expectation that false assumption tested by T times M s x (1/M s ) ^T <  1 .

At this time, the guessed values k_l , k_s that go through the test and the position ( e , f , g ) can be thought to be correct values.

In the same way, we can exhaust all the possible results when the three-dimensional plain-image pixel position (0, d ,0) after the pixel transformation, and set the transformed position is ( h , i , j ) . Due to the same reason that the three-dimensional generalized Cat mapping only

changes the gray position and not changes the gray value. So, ( h , i , j ) can choose the particular position that the pixel position (0, d ,0) has the same gray value in the plain-image and cipher-image, set the number of these pixels are M’ . For any w , the transformed position of (0, d , wd ) is ( h , i , j ) + w ( e , f , g ) , search the gray values of pixel positions (0, d ,0) ,     (0, d , wd ) ,     ( h , i , j ) ,

(h, i, j) + w(e, f ,g) in plain-image and cipher-image, then g (0, d, wd) = g'((h, i, j) + w (e, f, g))

Using this condition can check whether the assumed position ( h , i , j ) is right or not. Then test all the values of (0, d , wd ) , 0 <  w <  T '( T ' > 1) , the expectation that a wrong guessed value go through the all tests is M ’x (1,M’) ^T < 1 , so if ( h , i , j ) can go through all the tests, it would be thought to be correct position.

Now, we can exhaust all the possible transformed results of the three-dimensional plain-image pixel position (d,0,0) , and set the transformed position is (k, l, m) . Because of the three-dimensional generalized Cat mapping only changes the gray position and not changes the gray value. So, (k, l, m) can choose the particular position that the pixel position (d,0,0) has the same gray value in the plain-image and cipher-image, set the number of these pixels is Ms . For any w , the transformed position of (d,0,wd) is (k, l, m) + w(e, f ,g) , search the gray values of pixel positions (d,0,0) , (d,0,wd) , (k, l, m) , (k, l, m) + w(e, f ,g) in plain-image and cipher-image, then g (d ,0, w) = g'((k, l, m) + w (e, f, g))

Using this condition can check whether the assumed position ( k , l , m ) is right or not. Then test all the values of ( d ,0, wd ) , 0 <  w <  T '( T ' > 1) , the expectation that a wrong guessed value go through the all tests is M’x (1/M’) T < 1 , so if ( k , l , m ) can go through all the tests, it would be thought to be correct position.

In the end, using the obtained image transformed pixel positions ( e , f , g ) of (0,0, d ) , ( h , i , j ) of (0, d ,0) , ( k , l , m ) of ( d ,0,0) , we can get the equivalent transformation of the three-dimensional generalized Cat mapping. In a word, the complete attack algorithm can break the image encryption scheme. The following gives an equivalent key attack algorithm when the step 2 and step 3 only iterate only one time in the image encryption algorithm.

Algorithm 1:

• 1)    compute the greatest common factor d of N ;

• 2)    for ( k , = 0 ; k , <  2¹⁶ ; k , + + )

{ for (k, = 0 ; k, < 216; k, + +) {

• • 1 use the key generation algorithm to generate key parameters L_i and S ；

• 2 use the reversible transformation of the step 3

I (k) = ф(k) © C (k) © C (k -1) + M - ф(k )}mod M to decrypt the cipher-image.

• •    3 ( i , j , k ) ← the plain-image pixel coordinate of (0,0, d )

g (0,0, d ) ← the plain-image pixel gray value of (0,0, d )

• •    4 i 1=1 ；

5 if i1 > M’ , continue;

else ( e , f , g ) ← the pixel coordinate that the i 1th gray value of the chaotic cipher-image is g (0,0, d ) ;

• •    6 w=2；

• •    7 g (0,0, wd ) ← the gray value of the plainimage pixel (0,0, wd ) ;

• •    8 verification. To verify that

g (0,0, wd ) = g ’ ( we (mod N ), wf (mod N ), wg (mod N )) ;

if not, i 1++ return • 5

else to verify w <  7

If yes, w ++ return • 7;

else continue

• 3)    Output the transformed image position ( e , f , g ) of (0,0, d ) , and the values of k_l , k_s ;

• 4)    ( i , j , k ) ← the plain-image pixel coordinate of (0, d ,0) ;

g (0, d ,0) ← the plain-image pixel gray value of (0, d ,0) ;

• 5)    j 1=1;

• 6)    ( h , i , j ) ← the pixel coordinate that the j 1th gray value of the chaotic cipher-image is g (0, d ,0) ;

if ( h , i , j ) == ( e , f , g ) , j 1++, return 5);

• 7)    w =1;

• 8)    g (0, d , wd ) ← the plain-image pixel gray value of (0, d , wd ) ;

g '(( h , i , j ) + w ( e , f , g )) ^ the chaotic cipher-image pixel gray value of ( h , i , j ) + w ( e , f , g ) ;

to verify g (0, d , wd ) = g' (( h , i , j ) + w ( e , f , g ))

if not, j 1++ return 5);

else to verify w <  7

if yes, w ++ return • 7;

else continue;

• 9)    Output the transformed image position ( h , i , j ) of (0, d ,0) ;

• 10)    ( k , l , m ) ← the plain-image pixel coordinate of

( d ,0,0) ;

g ( d ,0,0) ← the plain-image pixel gray value of ( d ,0,0) ;

• 11)    k 1=1;

• 12)    ( k , l , m ) ← the pixel coordinate that the k 1th gray value of the chaotic cipher-image is g ( d ,0,0) ;

if ( k , l , m ) == ( h , i , j ) or ( k , l , m ) == ( e , f , g )

k 1++ ， return 11);

• 13)    w =1;

• 14)    g ( d ,0, wd ) ← the plain-image pixel gray value of ( d ,0, wd ) ;

g '(( k , l , m ) + w ( e , f , g )) ^ the chaotic cipher-image pixel gray value of ( k , l , m ) + w ( e , f , g ) ;

to verify g ( d ,0, wd ) = g '(( k , l , m ) + w ( e , f , g ))

if not, k 1++ return 11);

else to verify w <  7

if yes, w ++ return 13);

else continue;

• 15)    Output the transformed image position ( k , l , m ) of ( d ,0,0) ;

• 16)    By theorem 2, compute A using the results of ( e , f , g ),     ( h , i , j ) , ( k , l , m );

• 17)    To verify the obtained key using the plain-image and cipher-image

if yes, output the key; flag=1;

else flag=0; continue;

} if(flag==1) break;

}

Depending on the characteristic of the encryption algorithm transformation, the attack algorithm always can find the equivalent key. The maximal exhaustion complex of k_l and k_s is 2³², and computation complex of three pairs pixel positions ( (0,0, d ) , ( e , f , g ) ), ( (0, d ,0) , ( h , i , j ) ), ( ( d ,0,0) , ( e , f , g ) ) is M> M” + M? times. So, the whole attack algorithm computation complex is

O (2 32 ( M'_s + M S + M>

Next, we will give an attack algorithm when the step 2 and step 3 iterate more than one times. Because of the structure of the encryption is S-P type, the algorithm 1 can not attack it. Considering the three-dimensional generalized Cat mapping only infect six independent parameters. If the initialized image size is N 1 x N ₂ , and the every parameter’s exhaustion complex is

N = [V N । x N 2 _|, so the whole six parameters maximum exhaustion complex is N ⁶ « ( N , x N ₂)² , then the maximum equivalent key exhaustion complex is N ⁶ ® ( N 1 x N ₂)² when the algorithm iterates one times in this step. In step3, the key parameters is generated by the initialized key k_l and k_s , and the maximum exhaustion complex is 2³² in one iteration. When it iterates more than one times, [4][5] proposed a exhaustive attack on the algorithm. If every time the key parameters are generalized by the different 128-bit initialized key, set the iteration number is r , then the attack algorithm maximum computation complex is 2 32 r ( N ₁ x N ₂)² r . We give two different kinds of attack algorithm: algorithm 2 suitable for the encryption scheme that iterates many times and every round uses the same key; algorithm 3 suitable for the encryption scheme that iterates many times and every round uses different key.

Algorithm 2:

Exhaust the values of a ,b ,a ,b ,a ,b , where xxyyzz ax, bx, ay, by , az, bz e[0>N - 1];

{

• --- {

for ( k_l = 0 ; k_l <  2¹⁶ ; k_l + + )

{ for( ks = 0 ; ks < 216; ks + +)

{ generate Li , S ;

use the obtained key to decrypt the cipherimage;

verify the decrypted image and plain-image if yes, output the key, flag=1, break;

else flag=0, continue;

} if (flag==1) break;

} if (flag==1) break;

}

---}

Algorithm 3:

Exhaust all the values of every round key;

{

--{ generate Li , S ;

use the obtained key to decrypt the cipher-image;

verify the decrypted image and plain-image if yes, output the key, flag=1, break;

else flag=0, continue;

} if (flag==1) break;

• - --}

• V . THE ANALYSIS OF THE ATTACK VALIDITY

The maximum computation complex of the algorithm 1, 2, 3 are O (2³² M ) , 2³²( N 1 x N 2 ) 2 and 2³² r ( N 1 x N 2 ) 2 r . Take an 512 x 512 image encryption for example. Under the processing of the image encryption scheme, the value of N is N = V512 x 512 = 64 , even we assume that M s = 64³ (as we know, this is impossible, we can not obtain this cube). Under this condition, the maximum computation complex of algorithm 1 is

3 x 2³² M s = 3 x 2³² x 2¹⁸ <  2⁵²

And the computer complex is less than the number of key space of encryption key scheme, which is 2128. Compared with the popular data encryption standard (DES), which efficient key is 256, but it is not safe with the enumerate attacking. So, we can realized the attack under the current compute ability

When the image encryption scheme iterate more than one times of Step2 and Step 3, we can attack the scheme using the algorithm 2. By analyzing the algorithm 2, the key parameters are obtained by same 128-bit initial key. When the image encryption size is N ₁ x N ₂ , The maximum computation complex of algorithm 2 is

2³² x ( N 1 x N 2 ) 2 ,

When every key scheme iterates use different key parameters, and the number round of the image encryption scheme is r , then the maximum computation complex of algorithm 3 is

2^{32 r} ( N , x N 2 ) 2 ^r

In the same way, take an 512 x 512 image encryption for example. If the key parameters are produced by the same 128-bit initial key, the maximum computation complex of the whole algorithm is

2³²( N 1 x N 2 ) 2 = 2 ³² x 2 ³⁶ = 2 ⁶⁸

This result is less than the key space 2128.

We notice that all the computation results are less than the key number in the key space, meanwhile, both algorithm 1 and algorithm 2 can break the image encryption in the actual computation.

In the actual environment, in different round generally would not choose different independent key duo to the reasons such as key association. The use of the DES and AES can explain this point. Even if uses like this, Chen designed image encryption algorithm’s effective key also cannot achieve the anticipated goal

• V I. CONCLUSION

In this paper, some problems of a new image encryption scheme based on 3D Cat chaotic map are reported and three attacks on this cryptosystem have been presented. The main reason that Chen et al designed image encryption algorithm is not secure is the used chaotic transformation has a strong linear characteristic (proposed in [12][13][14]). And, the algorithm has equivalent key reducing the encryption secure strength.

In order to overcome this can introduce some nonlinear transformations and change the key union method. These results also show that before introducing a new transformation into cryptography field, we must study the properties of the transformation (proposed in [15][16]). Introduce the corresponding transformations to overcome the weakness of used transformation’s inherent weakness. Only in this way, the designed encryption algorithm can withstand the adversary’s cryptanalysis.