Improving Security of the Baptista's Cryptosystem Using Two-step Logistic Map

Published Online April 2015 in MECS

In last 4-5 decades, chaos theory has been developed by the efforts of many researchers by analyzing the behaviour of dynamical systems that are deterministic in nature but fully unpredictable. These are behaviourally random look like systems. Chaos theory has many applications in the field of physics, mathematics, chemistry, engineering etc [6]. Equally chaos is also used in random number generation [13], hash function [14] and cryptography [7], [9] etc. Chaotic cryptography is nowadays thrust area of research in data security (See, for instance, [1]–[10], [12], [15]–[17]).

In last 2-3 decades, many different chaotic encryption schemes have been proposed. The most used symmetric cryptosystem based on ergodic property of chaotic maps was given by M. S. Baptista [5] in 1998. The purpose of this paper is to propose the use of two-step logistic map to enhance the security of Baptista type cryptosystem.

In section II, Baptista’s algorithm and concept of dynamic look-up table in context of Baptista’s algorithm has been given. Also, two-step logistic map has been described. In section III, improved algorithm has been proposed in section IV, comparison of improved algorithm with previous schemes has been proposed. Finally, the paper has been concluded in Section V.

• II.    R elated W ork

  In 1998, Baptista [5] proposed a chaotic encryptiondecryption scheme using ergodic property of chaos, which attracted the researchers to make a fast and secure chaotic encryption-decryption scheme due to its simplicity and less complex structure. In the literature survey, we observed that first mapping of text characters with real values is done and then the algorithms are applied to encrypt the message. Decryption is performed by iterating map and then corresponding symbol for real values is obtained. The control parameter or initial seed or both were used as a secret key in all these chaotic cryptosystems [5], [16], [17]. Baptista type chaotic cryptographic algorithms covered in literature survey are described in next section.

• A.    M.S. Baptista’s Chaotic Cipher

  In 1998, Baptista [5] gave a symmetric encryption scheme based on ergodic property of chaos. In this

scheme a logistic map F : X → X as x n = r ∗ x n-1 (1 - x n-1 ) [5] is used as chaotic source. The logistic map’s output range is divided into intervals [Xmin, Xmax) ⊆ X . The number of intervals are S (where S is the number of symbols can be used in plaintext) and the range of each interval is e. So the each interval i is X_t = [X_min + (i - 1) * , X min + i * e) , where e =(Xmax - Xmin)/S .

Assume plain text is composed of S different characters {C_a1, C_a2 . . . C_aS}, use a one to one onto mapping f_S : X_t = {X 1 , X 2 , . . . , X S } ←→ A t = {C a1 , C a2 , . . . , C aS } to associate S different intervals with S different characters.

The procedure of encryption and decryption is as follows:

Given a plain text: T = {t 1 , t 2 . . .t i, . . . }(t i ⊂ A t ) .

The secret key : The initial condition x 0 and the control parameter r of Logistic map [5]

Encryption : For the first plain-character t 1 : Iterate logistic map from initial condition x 0 to find a chaotic state x n that satisfies that x n = t 1 → A t → X t , and record the iteration number as the first cipher-text c₁ if recorded value is greater than the base value else the process of iteration will continue till the conditions are satisfied.

For the i ^th plain-character t_i : Iterate the logistic map using previous x_n as initial seed and find the chaotic state x n that satisfy that x n = t i → A t → X t , and record the iteration number as the cipher-text c_i if recorded value is greater than the base value else the iteration process will continue. Perform this process for remaining plain text characters. This will give the cipher text corresponding to the plain text.

Decryption: For each value of cipher text, iterate the logistic map from previous condition and control parameters and get the corresponding plain text character as x n =X t → A t → t i .

In 2001, Li et. al. [8] analyzed chaotic cryptographic schemes and found that these systems are vulnerable to behavior analysis attack and guess of the initial condition. So in these chaotic cryptosystems all four types of cryptanalysis attack possible as cipher text only attack, chosen cipher text attack, chosen plain text and known plain text are possible [8]. They also proposed that rather than using a simple map a complex map can be used.

Alvarez et. al. [1] examined encryption schemes of Baptista [5]. They found three types of cryptanalysis attack on Baptista’s cipher: one-time pad attacks (chosen plain text), entropy attack and key recovery attacks [1]. They proved that it was a weak cryptosystem.

• B.    K. W. Wong’s fast chaotic cryptographic scheme with dynamic look-up table

  In 2002, K.W. Wong [16] gave a modified version of Baptista’s [5] chaotic cipher. Wong found that Baptista’s chaotic cipher was slow due to some extra comparisons and the scheme was not secure. Wong proposed a new scheme with a look-up table that was dynamically updated via swapping the associated symbols between two intervals [16]. Initially the lookup table was initialized according the ASCII values of characters. Update in the

look-up table will be performed after each block of plain text encryption and decryption. This scheme has a logistic map as the chaotic source and the initial condition and control parameter of logistic map as the secret key. The dynamic look up table’s i ^th entry will be swapped with j ^th entry using (1) as.

j =( i + ™m ∗ N ) mod. N (1) \ Xmax-Xmm. /

Where X is the current value and N is the number of entries in table. Other process will be same as original Baptista’s [5] chaotic cipher.

Alvarez et. al. [2] examined encryption schemes of Wong’s[16] look-up table and observed that the attacker can easily get the next position of the symbols without knowledge of the exact current value of X [2].

• C.    Improving the security of dynamic lookup table

  In 2006, Xiao, Liao and Wong [17] worked on dynamic look up table of Wong [16] and found vulnerabilities in the lookup table. They simplified (1) by updating as (2).

• 2 ∗ I mod N ≤   ≤ 2 ∗ I + 1 mod N (2)

Where J is the new index position for I ^th symbol and N is the total number of possible symbols in the plain text.

Further, to enhance the security of dynamic look up table to make Baptista’s algorithm more secure, they picked up third, fourth and fifth digit of the current value of X parameter for updating the dynamic lookup table entries [17]. Then I ^th indexed entry will be swapped with J ^th entry using (3).

= ( I +3 ^r(^digit ∗ 100+4 ^{1 ℎ} digit ∗ 10+

• 5 ^{1 ℎ} digit ) mod N              (3)

Where N is the total number of possible symbols in the plain text. Rest of the process will be same as Baptista‘s algorithm [5].

• D.    Two step Logistic map

  In 2009, Rani and Agarwal [11] gave a new study of the stability of logistic map, in which they enhanced the capabilities of logistic map via superior iterations. It is a two-step feedback mechanism in which new iterated value of x is calculated using previous two values of x with factor B ∈ (0, 1] as (4).

y n = r ∗ x n-1 (1 – x n-1 )

x n = B ∗ y n + (1 - B) ∗ x n- 1

where x ∈ (0, 1] and r ∈ [3.86, 4)        (4)

By using two-step logistic map, factor B also can be a part of the key by which key space will increase the security of such type of chaotic cryptosystems. So in the proposed scheme, we shall use a two-step logistic map to enhance the capabilities of chaotic cryptosystem.

• III.    U se O f T wo S tep L ogistic M ap I n B aptista ’ S C ryptosystem

Baptista’s type symmetric encryption schemes have less key space that is vulnerable to brute force attack. Behaviour of map varies with the change in values of control parameter by which behaviour analysis attack is possible. In addition, these are also insecure, as its present value acts as a seed for next condition. By which an adversary can get all next conditions, if present initial condition is known to him. The proposed scheme is a symmetric encryption scheme.

The scheme is as:

• a)    Take a 160 bit key as K 0 K 1 K2.......... K 159 .

• b)    Take two logistic maps in two steps [11] as (5) and (6) first for encrypting data and second for updating the lookup table.

x n = r 1 ∗ x n-1 (1 - x n-1 )

xn = b1 ∗ xn + (1 - b1) ∗ xn-1

y n = r 2 ∗ y n-1 (1 - y n-1 )

yn = b2 ∗ yn + (1 - b2) ∗ yn-1

• c)    Fix control parameter r1 and r2 between 3.86 and 4. d) Take keys values as (7), (8), (9) and (10).

Xq =∑?=o kt /2 i+i(7)

Уо =∑F=32 k[ /2 r-31(8)

Ь-L =∑1^64 k[ /2 i-63(9)

Ьг =∑1=95 kt /2 i-95(10)

• e)    Rest 32 bits of key will be used as updating parameters as (11), (12), (13) and (14).

KU1 = K128 . . . K135(11)

KU2 = K136 . . . K143(12)

KU3 = K144 . . . K151(13)

KU4 = K152 . . . K159(14)

• f)    Update the key after encryption of a block of data as

Discard left 16 bit x 0 . Then add keys KU 1 and KU 2 at the last of new x₀ . Now get the float initial condition x₀ from it and add with second logistic map output. This will be new initial condition for first map.

Discard left 16 bit y₀ and add the key KU₃ and KU₄ at the last of new x₀ . Then get float initial condition y₀ from it for second map.

g) Updating parameter will be updated as (15), (16), (17) and (18).

KU1 = KU1 ⊕ KU2 ⊕ KU4(15)

KU2 = (∼ KU1) ⊕ KU3 ∧ KU4(16)

KU3 = KU2 ∨ KU3 ⊕ (∼ KU4)(17)

KU4 = KU1 ∨ (∼ KU2) ∨ KU3(18)

• h)    Update the Look up table via shuffling the entries and get the new associated intervals for the symbols based on second map value by iterating it number of times the symbols previous position and J^th entry will be swapped with i^th entry using (19).

( i+∗N) mod N    (19)

Where e is interval, e2 is the current value of initial parameter of second map and N is the total number of possible symbols in plain text. The associated interval will be [Xmin + i ∗ e + e2, Xmin + (i + 1) ∗ e + e2) .

• i)    In proposed scheme, the Lookup table will be as Fig.1. This is the fully dynamically updated look-up table, which will be the part of security. In this lookup table, there will be N + 1 interval where N is the total number of possible symbols in plain text. So the value of e will be calculated as (20).

X max—X min

N+l

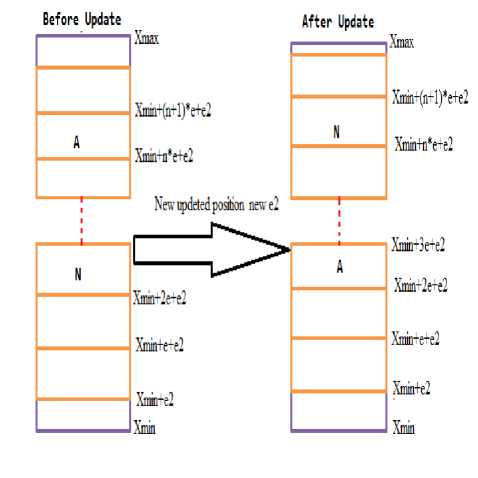
Fig. 1. Fully dynamically updated lookup table

• j)    Other process will be same as original Baptista’s chaotic cryptosystem. The encryption process can be seen in Fig. 2.

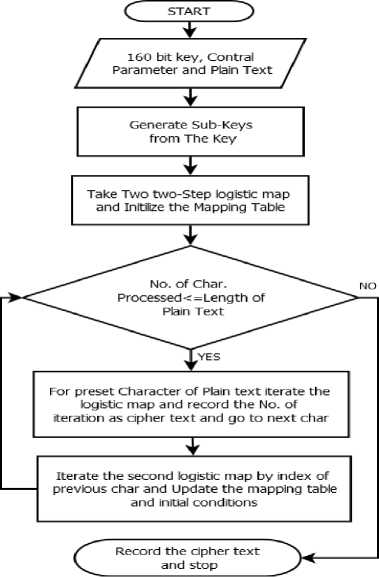
Fig. 2. Proposed encryption process

• k)    Decryption process will be same as encryption. It can be seen in Fig. 3.

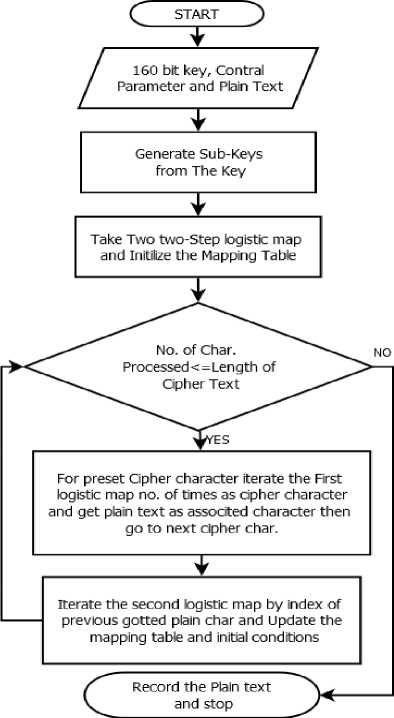
Fig. 3. Proposed decryption process

• IV.    C omparison W ith E xisting S chemes

The proposed scheme has been implemented and tested using Java development kit (jdk 1.7.0) on windows platform. System configuration consists of Intel Pentium dual core (1.86GHz), CPU with graphic and 2GB RAM. This scheme with existing schemes: Baptista’s cipher, Dynamic look-up table cipher (DLT) and improved dynamic lookup table cipher (IDLT) has been compared using similar conditions and plaintexts. Then the results are compared to see the performance of proposed scheme. The first two comparisons shows the avalanche effect that if small number of bits are changed in plain text or the keys then it should show the large number of bits change in cipher text

• A.    Hamming code distance comparison

  Hamming code distance is defined as the number of different bits in two strings. In other words if str1 and str2 are two strings, then number of bits required to change the first string str1 to str2 is known as hamming code distance. For the proposed scheme, key = “qwertyuio pasdfghjklz” and control parameter r = 3.897654321 has been chosen. For other schemes also, similar generated initial condition x₀ =0.4432280925102532 and control parameter r =

  3.897654321 has been chosen. These have been used for different plain text inputs and then cipher-text outputs have been analysed by calculating hamming code difference. The plain texts str1, str2and str3 are as:

str1: “hi security hi cryptography”

str2: “hi tecurity hi cryptography”

str3: “hi teduruty hi cryptography”

Table 1. Hamming Code Difference Comparison for Different Plaintext

String	H.distance	Baptista	DLT	IDLT	PROPOSED
str1 str2	3	19	39	37	78
str1 str3	5	12	56	57	96
str2 str3	2	10	17	20	76

From Table 1 we can see that the new proposed scheme has more Hamming code distance than the previous one Baptista type cryptosystem for change in the plaintext. This means that the proposed scheme have more avalanche effect that makes it more secure. Also, we have observed the hamming code distance for small change in the key for proposed scheme as Key1=“qwertyuiopasdfg hjklz”, key2= “rwertyuiopasdfghjklz” and key3=“ruerty uiopasdfghjklz”, and control parameter r = 3.897654321 . For other schemes, we used the similar generated initial conditions x 01 = 0.4432280925102532 , x 02 =0.447134342 5102532 and x 03 =0.4471038249321282 and control parameter r = 3.897654321 . Same plain text is taken as “hi security hi cryptography”. The comparison of results is shown in the Table 2.

Table 2. Hamming Code Difference Comparison for Different Keys

Keys	H. distance	Baptista	DLT	IDLT	PROP OSED
Key1 Key2	2	42	46	47	55
Key1 Key3	4	54	62	69	72
Key2 Key3	2	40	42	41	44

From Table 2, we can see that proposed scheme has also more hamming code distance than the previous one Baptista type cryptosystems with small change in key.

• B.    Levenshtien distance/Edit distance comparison

  If str1 and str2 are two strings then edit distance or Levenshtien distance is the number of characters replacements to covert str1 to str2. For comparison, we choose the key as “qwertyuiopasdfghjklz” for proposed scheme and similar generated initial condition x₀ = 0.4432280925102532 and control parameter r = 3.897654321 for all other schemes. We chose three different plain text strings as:

str1: “hi security hi cryptography”

str2: “hi tecurity hi cryptography”

str3: “hi teduruty hi cryptography”

Table 3 shows the comparison of output cipher texts for different schemes, the results of this table shows that the proposed scheme gives better results.

Table 3. Edit Distance for Different Plaintexts

String	H.distance	Baptista	DLT	IDLT	PROPOSED
str1 str2	1	12	26	28	68
str1 str3	2	8	37	35	67
str2 str3	1	5	11	9	62

C. Cipher text Distribution

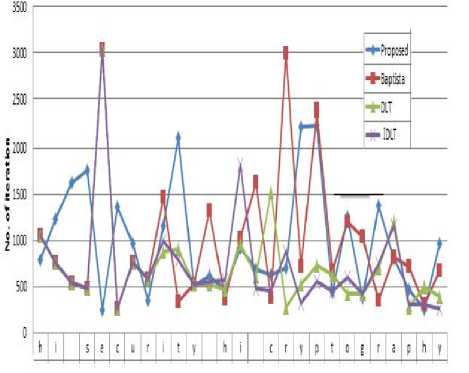
To compare the cipher text distribution, we choose the same plain text as “hi security hi cryptography”. For proposed scheme, the key is taken as “qwertyuiopasdfghjklz” and control parameter r = 3.897654321. For other schemes similar generated initial condition x 0 = 0.4432280925102532 and control parameter r = 3.897654321 has been used. Fig. 4 shows similar cipher text distribution for different schemes and the proposed scheme.

• D. Performance Comparison

  Performance analysis is done on the basis of time required to perform the encryption and decryption operations. For this purpose, we have chosen key = “qwertyuiopasdfghjklz” and control parameter r = 3.897654321 for other schemes similar generated initial condition x0 = 0.4432280925102532 and control parameter r = 3.897654321. By using ten strings of different length as plain text input, we have calculated encryption and decryption time for proposed scheme as well as existing schemes.

From Table 4 and Figs. 5 and 6, it can be observed that proposed scheme require some more time to perform encryption-decryption operations

Table 4. Execution Time Comparison in Microseconds

String Size in Bytes	BAPTISTA		DLT		IDLT		PROPOSED
	Enc.	Dec	Enc.	Dec.	Enc.	Dec.	Enc.	Dec.
10	2130	941	2999	1380	2345	955	3451	1453
20	5328	2743	6967	2773	5091	2234	7984	3142
30	6426	4431	7804	6054	8946	6256	9638	6801
40	9726	6246	12711	6270	12910	6289	17145	6965
50	12763	4536	14005	5603	13688	5742	17269	7219
60	15136	5187	15294	7695	18352	7529	24058	8351
70	27812	9795	28568	6262	30866	12540	39865	15460
80	110944	8923	110673	11779	110286	13261	115917	18609
90	111902	8624	101492	10015	111048	9628	117672	17809
100	118999	10589	118350	10605	118710	10421	181938	17079

From Table 4 and Fig. 5, it can be observed that the encryption time of proposed scheme is less than 1.5 times of the previous schemes and sometimes it is nearer to the previous schemes.

Fig. 4. Cipher text distribution comparison

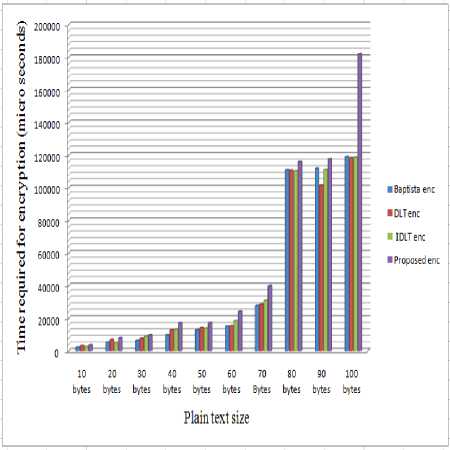
Fig. 5. Encryption time comparison

From Table 4 and Fig. 6, it can be observed that time for decryption process is about 1.4 times of the previous schemes, so decryption time is slightly more than previous schemes.

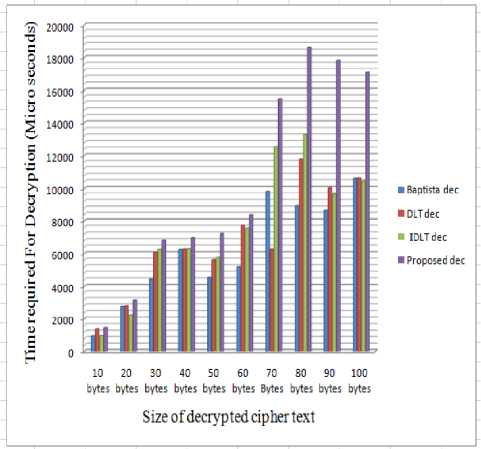
Fig. 6. Decryption time comparison

• V. C onclusion

  Proposed scheme has two two-step logistic map, one for encryption and another for updating the initial condition and the table entries. The proposed system has 160 bit key that provide 2160 different key combinations. It resists the proposed cryptosystem against Brute-force attack. The experimental results shows that the proposed scheme require some more time for encryption and decryption of data then Baptista’s cryptosystem, Wong’s dynamic look-up table cryptosystem and Improved dynamic look-up table cryptosystem. The comparisons based on Hamming code distance and edit distance shows that the proposed cryptosystem have more avalanche

effect than Baptista’s cryptosystem, Wong’s dynamic look-up table cryptosystem and improved dynamic lookup table cryptosystem. Updating the initial condition after each encryption makes it secure from known initial condition and control parameter i.e., known partial key. The control parameter is also fixed in this scheme, so map behaviour is fixed in all states. This resists proposed scheme against behaviour analysis attack and partial key recovery attack.

The proposed method has been tested with only text information. It has a future work that it can be implemented for other types of information like images, video etc. Further, it can be used with some more feedback factors by making the new iterated value based on more than two previous values. Such type of mechanism can also be developed for making a chaotic hash function

A cknowledgment

This work was supported in part by a grant from Research and Development Cell under ICT Cell Central University of Rajasthan. The authors want to thank the Coordinator and members of this cell for their valuable support.