Improving the Performance of Routing Protocol using Genetic Algorithm

Published Online July 2016 in MECS

Routing tables are built, using a lot of routing algorithms which help to find the path from source to destination[1]. OSPF is one such algorithm, which helps us to find the shortest path between each source and destination. The limitation here is that of the overloading, in the shortest path or link congestion occurring anywhere in between. The arrival of the packets at the desired destination with the delay or queuing on the way or router processing can result in service quality being affected. All these limitations can be taken care of by optimization of IP network. Path adjustment can lead to better utilization of network resources and thus an improvement in QOS. It can therefore be safely said that the basis of planning and managing networks is Routing Optimization[4].

Genetic Algorithm (GA), an evolutionary and optimization algorithm, is the answer to this. It puts forward a solution, to find paths which are good alternatives against the overloaded path between source and destination. GA is a programming methodology which imitates biological evolution as a strategy for problem solving[2]. It is said to be the most upcoming area of Artificial intelligence. Darwin’s evolution theory “Survival of the fittest” inspires GA. This is due to the individual competition in nature for resources which are normally scanty resulting in the individual which are the fittest to dominate the weaker individuals[8].

The basic steps that comprise a genetic algorithm are

• 1.    Initialization – An initial population is created. The population is generated randomly and can be of any size, that is, from only a few individuals to thousands.

• 2.    Evaluation – The members of the population are then evaluated and a 'fitness' for that individual is calculated. How well the individual fits in with the desired requirements helps to calculate the fitness value [5].

• 3.    Selection – Improving the overall fitness of the population has to be the final goal. By means of selection, the bad designs are discarded and the best individuals in the population are kept back. Individuals with better fitness values to be selected for the next generation, has to be the basic idea.

• 4.    Crossover – New individuals are created by the combination of aspects of selected individuals. By combination of certain traits from two or more individuals, a better offspring is created which will inherit the best of traits from both the parents.

• 5.    Mutation – A little bit of randomness, needs to be added to the population genetics [15]. This is essential so that combination of solutions created would be in our initial population. To an individual’s genome, small changes done at random are called mutation.

• 6.    After the second generation is obtained, step 2 is started again till step 5 is reached.

Whenever a problem, has to be solved, the GA input is a set of solutions to that problem, which are encoded in a particular fashion. A metric called a fitness function is used to evaluate each candidate quantitatively. Therefore GA is used to carry out evaluation of each candidate, according to the fitness function. Some candidate will not work at all, some show activity and some are very promising. The ones which are promising are allowed to reproduce. Multiple copies are made and because of random changes during the copying process, all the copies may not be perfect. The digital offspring, thus generated are then allowed to go on to the next generation giving rise to a new set of candidate solutions.

Second round of fitness evaluation is carried out next. Some solutions which do not get better are deleted, and where improvement is seen are selected again and copied over for the next generation with certain random changes carried out. This process is repeated again till the best solutions are obtained. In order that a GA is used to work on any problem, the first important thing that needs to be done is that a method has to be adopted, so that a potential solution to the problem are encoded in a way that a computer can process. The first and easiest way is to encode solutions as binary sequences of 0’s and 1’s which has been adopted in this paper. Here the digit in each position represents the value of any aspect of the solution. The second approach is to encode the solutions as integer or decimal number arrays and the third approach is to present the individuals as letter strings[12]. Fig.1 below indicates the parameters required for optimum path determination and Fig.2a and Fig.2b represents an example of overloaded and optimal routing for the two traffic flows.

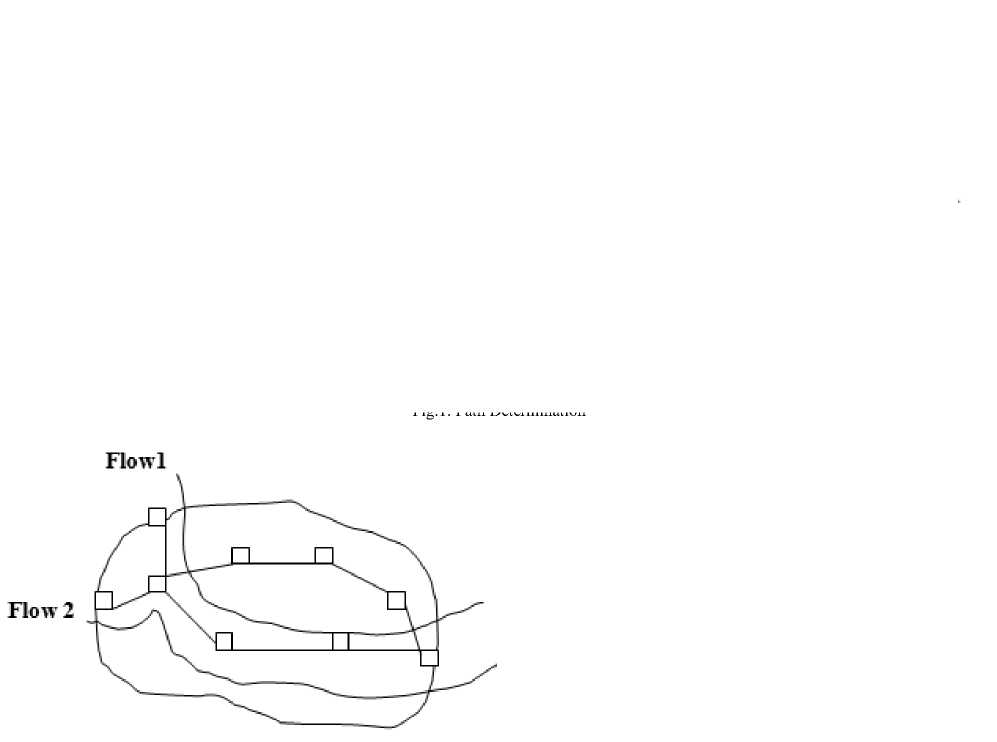
Fig.2a. Overloaded Routing

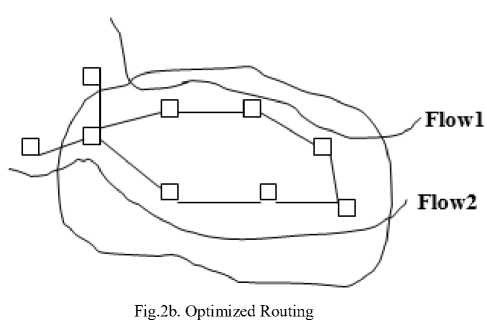
For the left hand side figure 2a, the network shows both traffic flows sharing several links, even though being the shortest path from source to destination, could lead to overloading the shortest path. For the right hand side figure 2b, routing is carried out in such a way that the two flows have no link in common. This gives a better performance. We have taken only two traffic flows here, so figure 2b is the obvious solution, but when there are thousands of individual traffic flows, algorithms and methodologies are important for optimization.

This paper is organized into six sections. Section I provides the introduction of GA. Section II discusses the related works and Section III gives detailed overview of network analysis of GA. Section IV deals with the methodology adopted and how NS3 is used for analyzing the behavior of the network under consideration. Section V talks about the variations of certain parameters for the routing protocols under consideration. In other words Section V comprises the result analysis. Section VI discusses the conclusions drawn and the future scope.

• II.    Related Works

  Munemoto et. al (2011) talks about the chromosomes of variable length being used for problem encoding. Here few crossover sites are used for a feasible solution exploration. In other words, we can say that crossover is position dependent.

Inagahi et.al (2011) discussed an algorithm which uses chromosomes of fixed length. These chromosomes (candidates) are integer sequences and every node has an identification which is obtained by random selection from the set of nodes. For the crossover phase, the genes that are selected from parent chromosome is put in that of the offspring.

Here offsprings may also generate new chromosome, which resemble the initial chromosome in fitness. This retards the evolution process.

Ramakrishna et. al (2012) describes how to work on fixed and variable length chromosomes, but it is not essential that optimal path is obtained in all cases.

Obeidat et. al (2012) puts forward an algorithm which is a combination of GA and network delay analysis. They proposed that GA would give better optimal path regardless of what network topology is used or whatever changes in node or link take place.

Biradar et.al (2013) analyzes routing in manets and uses GA to improve the performance of Adhoc on demand multipath distance vector routing (AODMV). This paper allows, changes by a node, in the routing information in a quick and efficient way, by allowing lesser link breakages and adjustment in the changing local topology.

Chaudhary et.al (2011) proposed a strategy, GA based to find the optimal path between two nodes. In this paper variable length chromosomes and their genes are used for encoding purposes. Here the crossover operation exchanges the routes which are partially laid out at crossover sites which are independent and the mutation operation is responsible for maintaining the population’s genetic diversity. Figure 3 below shows the complete flow of events that takes place in a genetic algorithm.

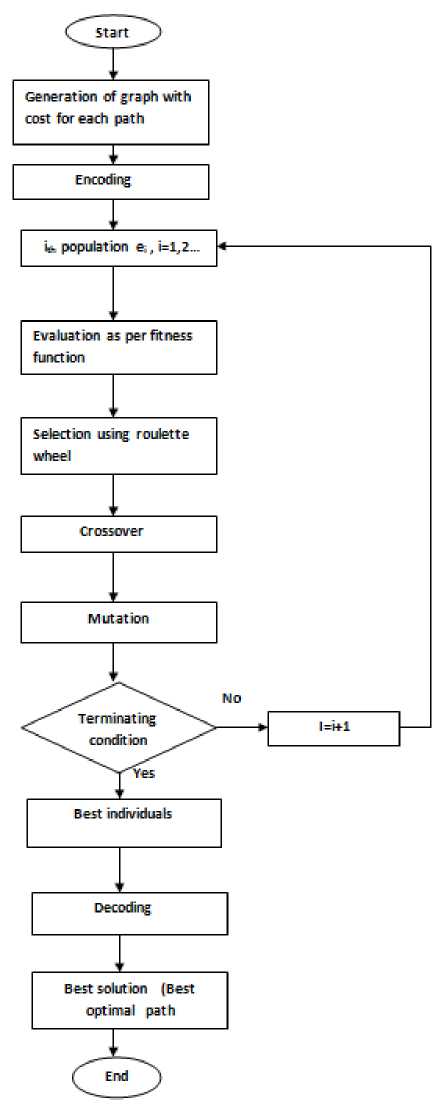
Fig.3. Flow Chart Of GA

• III.    Network Analysis Using Ga

The below mentioned steps are carried out in optimization of network using GA.

Step1 : A graph is generated with each path cost mentioned. The network represented by nodes is formulated by means of a graph and assignment of cost to a link that connects two nodes is done randomly. The source and the destination nodes are chosen to generate all the paths between desired nodes. Whenever cost = 0

for a link between two nodes, this indicates there is no link connecting the two nodes. Consider the network shown in figure 4 for application of GA.

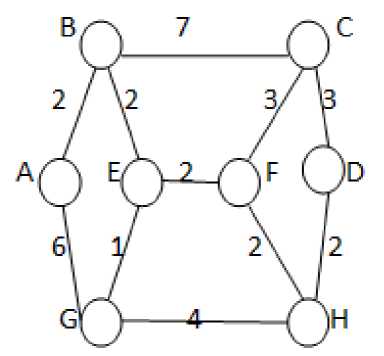
Fig.4. The network to be Analysed

Step 2: Coding of individuals is composed of m strings. Each e i represents the distance between nodes where i = 1,2,3…….m. Let e 1 = AB = 2, e 2 = BC = 7, e 3 = CD = 3, e₄ = GH = 4, e₅ = AG = 6, e₆ = EF = 2, e₇ = BE = 2, e₈ = CF = 3, e 9 = DH = 2, e 10 = FH = 2, e 11 = GE =1.

Step 3: Minimum distance from source to destination with continuity comprises the fitness function.

Step 4: Selection of initial population is the next step . This is randomly generated based on the distance between nodes. Distance is coded in 4 bit strings and the total string length = 4*5 = 20 bits.

Take for instance 4 candidates or individuals as initial population.

• a)   e2(7)  e4(4)  e3(3)  e5(6)e

• b)   e 1 (2) e 11 (1) e 5 (6) e 2 (7) e 6 (2)

• c)   e4(4)  e7(2)  e8(3)  e11(1)e

• d)   e1(2)  e3(3)  e6(2)  e2(7)e

Sum of edges for a) = 23

Sum of edges for b) = 18

Sum of edges for c) = 12

Sum of edges for d) = 16

Step 5: Apply two point crossover after seventh and sixteenth bit, on the initial population.

Before crossover, randomly generated individuals / candidates are as follows:

8421 8421  8421 8421 8421 Sum of edges

• a)  0111 0100 0011 0110 001123

• b)  0010 0001 0110 0111 001018

• c)  0100 0010 0011 0001 001012

• d)  0010 0011 0010 0111 001016

After, applying two point crossover, the individuals obtained are as follows:

8421 8421 8421 8421 8421 Sum of edges

a)	0111	0101	0110	0111	0011	28
b)	0010	0000	0011	0110	0010	13
c)	0100	0011	0010	0111	0010	18
d)	0010	0010	0011	0001	0010	10

Step 6: Mutation is implemented by replacing first four bits with source and the last four bits with destination node values. For the network under consideration A is the source node and D is the destination node. Lowest weight associated with both is 2 that is replace both by 0010. Therefore the new set of individuals obtained are as follows:

8421 8421 8421 8421 8421 Sum of edges

• a)  0010 0101 0110 0111 001022

• b)  0010 0000 0011 0110 001013

• c)  0010 0011 0010 0111 001016

• d)  0010 0010 0011 0001 001010

Step 7: As already specified earlier, the fitness function = min ∑ e_i with continuity.

After mutation the minimum path length from source to destination, that is A to D is case d above which is written as follows:

0010 0010 0011 0001 0010

This can be decoded as the path AB BE FC EG FH. But this is not a continuous path.

After many iterations we get the minimum path length with continuity as follows:

0010 0010 0010 0010 0010

which can be decoded as the path AB BE EF FH HD. This is the most optimal path.

• IV.    Methodology

NS3 is an event driven simulator used for simulating wired and wireless networks. It is used to analyze events to have a better understanding of the behavior of networks. The above discussed steps are now applied to the topology, shown in Fig. 5, which is used to study the performance of routing protocols OSPF and OSPF, plus GA by varying packet sizes. NS3 simulator is used to analyze the behavior and performance of routing protocols OSPF and OSPF plus GA [4]. The flow monitor in NS3 is a few lines of code and it measures all flows in the simulation.

Fig.5. Topology Considered

• V.    Result Analysis

The main focus in this paper, is on the effect of packet sizes on throughput, packet delivery ratio, packet loss and delay for routing protocols OSPF and OSPF plus GA OSPF as shown below in Tables 1 and 2 respectively.

Table 1. Throughput, PDR, Packet loss, Delay and Jitter values for OSPF Normal

PKT SIZE	THROUGHPUT (Kbps)	PACKETS SENT	PACKETS RECEIVED	PDR %	PACKET LOSS	TOTAL DELAY (Sec)	JITTER (Sec)
200	27780.4	15624	15596	99.82	28	0.00898938	0.00299646
400	26074.6	7812	7798	99.82	14	0.00899417	0.00299806
600	25502.7	5208	5198	99.83	10	0.00899781	0.00299927
800	25221.7	3906	3899	99.82	7	0.00900375	0.00300125
1000	25049.5	3124	3119	99.83	5	0.00901027	0.00300342
1200	24934.2	2604	2599	99.80	5	0.00901218	0.0030040

Table 2. Throughput, PDR, Packet loss, Delay and Jitter values for OSPFNormal plus GA

PKT SIZE	THROUGHPUT (Kbps)	PACKETS SENT	PACKETS RECEIVED	PDR %	PACKET LOSS	TOTAL DELAY (Sec.)	JITTER (Sec.)
200	29472.6	18218	16546	90.82	1672	0.0315656	0.0105219
400	30421.4	9109	9098	99.88	11	0.00570342	0.00190114
600	29756.4	6072	6065	99.88	7	0.00570853	0.00190284
800	29426	4554	4549	99.89	5	0.00571363	0.00190454
1000	29225.7	3643	3639	99.89	4	0.00571843	0.00190614
1200	29088.2	3036	3032	99.87	4	0.00572197	0.00190732

THROUGHPUT

35000 7зоооо g 25000 t 20000 | 15000 g 10000 I 5000 0

■ OSPF

■ OSPFPLUSGA

200 400 600 800 10001200

Packet Size (Bytes)

Fig.6. Packet size vs Throughput

It is observed that, as the packet size increases, the number of packets sent and received automatically decreases in the two configurations shown in Fig. 6. Further, throughput is highest in OSPF, plus GA followed by OSPF. Packet loss in OSPF, plus GA is less than OSPF. As the packet loss is less in OSPF plus GA technique, it is therefore the technique which is more beneficial and to be used in future.

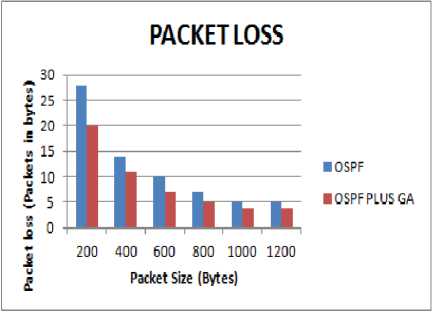
Fig.7. Packet size vs Packet loss

The packet delivery ratio is higher in OSPF, plus GA as compared to OSPF as is shown in Fig. 8. This is due to the larger number of packets being sent and received in OSPF plus GA. This again tells us that OSPF plus GA is the better technique.

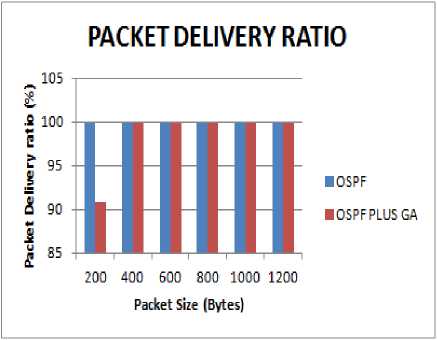
Fig.8. Packet size vs Packet Delivery Ratio

Also delay and jitter values are the least in OSPF, plus GA because of very fast recovery in case of link and node failures as compared to OSPF reconvergence time as shown in Fig. 9 and Fig.10. All the above results confirm the fact that OSPF plus GA is the technique that should be used for finding the most optimal path for sending packets of data.

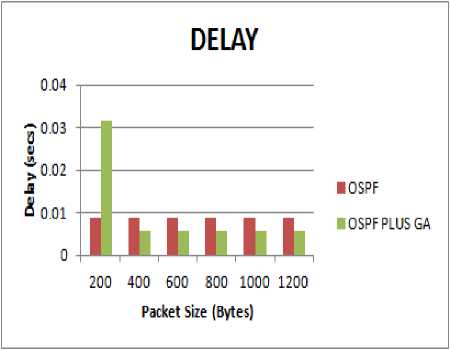
Fig.9. Packet size vs Delay

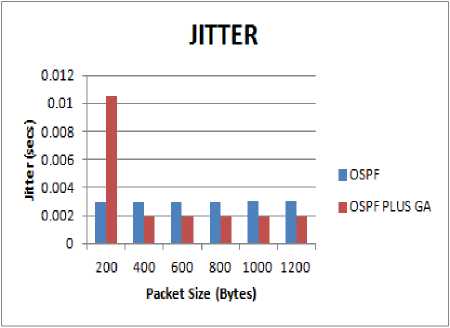
Fig.10. Packet size vs Jitter

• VI.    Conclusion and Future Scope

This paper features selection of an optimal path using genetic algorithm. The scheme used for coding, here was an efficient one. Length of the chromosomes is dependent on the number of existing nodes in the network. NS3 environment is used to search for the shortest path. Some future work can be done to reduce the chromosome length in case of networks with a higher number of nodes. The performance can further be improved by, mapping, geographic information with information of destination by taking into account route selection at various stages. Improvements can also be carried out in terms of better crossover and mutation probabilities.