Improving the sharpness of digital image using an amended unsharp mask filter

Published Online March 2019 in MECS DOI: 10.5815/ijigsp.2019.03.01

The blur effect is one of the famous and most frequent degradations to occur in digital images, in which it severely reduces the visual quality of an image, making it difficult to perceive the important details properly. The perception of humans is extremely sensitive to details and edges of an image. Since digital images consist primarily of high-frequency components, the perceived quality of an image can be highly corrupted if the high-frequencies are attenuated or eliminated [1]. Oppositely, improving the high-frequency components of an image can yield enhancements in the perceived quality [2].

Image sharpening denotes any improvement technique that enhances the visual quality of edges and details in an image [3,29]. This technology is extensively used in the photographic and printing industries for improving the apparent sharpness (acutance) in digital images [4]. In general, many reasons exist to increase the sharpness of an image, including overcoming the blur effect introduced by the camera equipment, drawing attention to specific image regions and improving the legibility. To achieve the sharpening procedure, different techniques exist, in which their complexities vary depending on their concept. Thus, a review of the literature regarding such techniques is delivered in Section II of this article. Among the existing techniques, the unsharp mask filter has received significant attention from researchers in the past decade due to its simplicity in processing various types of images. Still, it is known that this filter can cause artifacts and reduce the true value of different images [28]. Among such artifacts, the overshoot effect is often introduced to the processed image [16,30].

This effect occurs around side-planar edges, making such edges appear with noticeable white shades around them [17]. Hence, it is essential to enhance the traditional unsharp mask filter in order to produce effect-free results with better acutance. Despite the significant advancement in this field, the chances of improving this filter are still available. Hence, an amended unsharp mask filter is proposed in this article, in which its main aim is to deliver images with better sharpness, without introducing any undesirable effects. In the developed filter, the image is smoothed by using the traditional bilateral filter and then blurred using a modified Butterworth filter instead of blurring it with a Gaussian low-pass filter only as in the traditional unsharp mask filter.

This approach allowed to eliminate the introduction of the unwanted overshoot effect and to recover images with better visual quality. Finally, the proposed filter is assessed using two modern image quality assessment metrics, real and synthetic-blurred images, and is compared with three renowned image sharpening techniques. Experimental results revealed that the proposed filter can produce better results than its original counterpart and the compared techniques. The rest of this article is arranged as follows. In Section II, a sufficient review regarding the previous research works is given. In Section III, the proposed filter is explained in detail. Results and related discussions are delivered in Section IV. Lastly, a concise conclusion is provided in Section V.

• II.    Related Works

In this section, certain research works are explained to highlight specific key concepts that are used previously in the field of image sharpening. In [5], the authors tested various iterative morphological operators to sharpen a given image. In their study, they proved that operators that utilize a concave structuring function can be utilized successfully for image sharpening. The parameters of the used operators are determined based on the amount of the blurring effect that is detected in the input image.

In addition, the author of [6] introduced an APEX technique for image sharpening. This technique depends on the utilization of a certain limited class of shiftinvariant blurs that is possible to be expressed as finite convolution products of two-dimensional radially symmetric Lévy stable probability density functions. This technique cannot be applied to all images. However, it has a great potential to process medical and remote sensing images as proved by various achieved tests. Likewise, the authors of [7] proposed an optimal unsharp mask filter, in which it works by applying a high-pass filter on the input image. As well, the input image undergoes a pixel classification process using a Laplacian of Gaussian operator and the output of such process undergoes further processing and is augmented by a strengthening parameter. The output of this process is multiplied by a high-pass filtered image, and the outcome is added to the original image to produce the final result.

What is more, the authors of [8] proposed a sharpening technique that depends on the human visual model, in that it mixes certain spatial filters with the Laplacian of the Gaussian operator. The final result of this technique is obtained by using the alteration deduces of the original image. Moreover, the authors of [9] developed a new technique that works by decreasing the width of the edges via a fuzzy inverse diffusion with the aid of the detected gradient direction and a specific forward diffusion of the tangent direction. A second order Gaussian smoothing is utilized as well to choose the proper zero crossing which helps in providing adequate noise suppression in the sharpening process. The used fuzzy membership function is controlled by the gradient magnitude of the image and the used diffusion coefficients are tuned locally based on the image directional derivatives.

Similarly, the authors of [10] used the local coupling concept with the shock-diffusion equation to sharpen an image. In this technique, the shock-diffusion is used to process the edges, while a standard-diffusion is utilized to remove the noise and other generated artifacts. A hyperbolic tangent function is used as well to overcome the untrue outcome with piecewise constant areas created by the zero-crossing process, while the local coupling aspect is used to provide an additional processing control for the sharpening process. Moreover, the authors of [11] developed a histogram-based technique for image sharpening. This technique starts by dividing the image into many partitions based on the smoothed pixel values that are acquired by processing the input image by a Gaussian filter. A special transformation function that considers both the neighboring pixel values and pixel value itself is applied to produce the final outcome.

In contrast, the authors of [12] introduced a technique that employs the Sobolev gradients for image sharpening. In this technique, the isotropic diffusion is used, wherein the equations related to ascent and descent are acquired by adopting the L2 metric to a certain Sobolev metric as well as, the Sobolev flow is implemented in the backward direction to get the sharp image. In [13], the author proposed two new nonlinear image sharpening techniques, in which the first involves the utilization of fully-color pseudo of the top-hats transformations, while the second involves the utilization of a three-state toggle contrast operator with the famous morphological operations of dilation and erosion. In [14], the authors developed a new technique that utilizes a multiscale image analysis procedure to determine some important variables that are used in the computation of the bright differential responses in various spatial scales. The actual sharpening happens when the determined brightness values are subtracted from those of the input image.

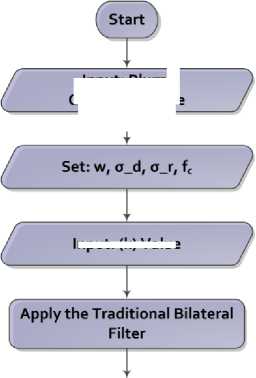
Input: (к) Value

Input: Blurry Grayscale Image

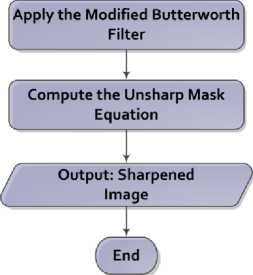
Fig.1. Framework for the proposed filter.

Finally, the authors of [15] developed a sharpening technique that utilizes both concepts of image fusion and wavelets. This technique starts by denoising the input image via a two-dimensional dual-tree discrete wavelet transform method to obtain a noise-free image. Then, this image is further processed by five different sharpening procedures. The final outcome is acquired by utilizing a wavelet-based fusion method. As seen from the reviewed techniques, different concepts have been used for image sharpening. However, most of such techniques require high calculations to provide the final result. Hence, the main motivation of this study is to provide a sharpening technique that utilizes a few calculations to produce lucid results with high acutance.

w r ( i , ^j ) = exp ‘

{ I ( i, j ) - I ( X, y ) } 2 2 » ;

w ( i,j ) = W ( i,j )• wr ( i,j )

• III.    Proposed Filter

In this section, the proposed filter is described thoroughly. The proposed filter starts by inputting a blurry image and the parameters for the subsequent procedures. The parameters are set to be w=5, σ d =3, σ r =0.1 and f c =120. It is important to mention that σ d is the same as σ s in the subsequent equations. Next, the bilateral filter is implemented to smooth the image and attenuate its high-frequency components. If the result of this filter is utilized directly with the unsharp mask filter, a halo may appear around certain edges in the final resulting image. Thus, the image produced by the bilateral filter is further blurred by a modified Butterworth low-pass filter to avoid the generation of such an undesirable artifact. After that, the result of this step is passed as an input to the unsharp mask filter to obtain the final resulting image. In the following sub-sections, appropriate explanations regarding the major phases of the proposed filter are provided to well-comprehend the operation specifics of this filter. To end with, Fig. 1 illustrates the framework of the proposed filter.

• A.    Bilateral Filter

  This filter was initially developed by Smith and Brady under the name of “SUSAN” in 1997 [23]. Later, it was revived by Tomasi and Manduchi [24] who named it the “bilateral filter”, which is now the most frequently utilized name. This filter is deemed a nonlinear smoothing technique because its output is a weighted average of its input. Also, it works in a similar way as the Gaussian convolution in producing a weighted pixels average. However, the dissimilarity is that this filter has considered the variation of intensities to preserve edges and fine details. The advantage of the bilateral filter lies in the selection of the similarity of two pixels, where it examines if their spatial distance is sufficiently near and if the intensity values are similar or not. When an image I is inputted, the resulting image from the bilateral filter I^BF ( x , y ) for a pixel (i,j) can be determined as follows [25]:

I B ( X , y ) =

E w (i, j) I (i, j) Z w(i, j)

where σ s and σ r represent the two standard deviation parameters that define the extension of two Gaussian kernels. The bilateral filter is controlled by σ s and σ r . These two parameters can regulate the decline of the two weight factors. When increasing the value of parameter σ r , the output of the bilateral filter becomes somewhat similar to Gaussian blur. When the values of both parameters are large, the output of the bilateral filter is transformed to an average one.

• B.    Butterworth Filter

A Butterworth low-pass filter is a well-known method for image blurring. It keeps frequencies inside the radius D 0 and castoffs the values outside it to provide a gradual alteration from 0 to 1. The equation of a Butterworth low-pass (BLP) filter of n order and a distance cut-off frequency D 0 is defined using the following equation [26]:

H ( u, v ) =

1 +f D ⁽ u , v ) )' I   D O   J

where, D ( u , v ) represents the distance from the point ( u , v ) to the frequency center, wherein it is computed based on the input image in the frequency domain; H ( u , v ) is the blurring mask generated by the BLP filter. The basic model for filtering a given image is achieved by converting the input image to the frequency domain I ( u , v ), then multiplying it by H ( u , v ) using the following equation [27]:

B ( x , y ) = ifft [ I ( u, v ) • H ( u, v ) ]

where, B ( x , y ) is the resulting image. In this study, a modified version of the above filter is used, in which the order n parameter is deleted to reduce the number of inputs to the proposed filter and to obtain better-blurred results when it comes to the smoothed image by the bilateral filter. The modified BLP filter can is determined using the following equation:

where, the overall weights mask w ( i , j ) is acquired by calculating the product of two dissimilar masks in the intensity w r ( i , j ) and spatial domains w s ( i , j ) using the subsequent equations:

1 +

T ( X, y ) = ifft [ I BF ( u , v ) • H ( u , v ) ]

where, Ḋ ( u , v ) is computed from image I^BF ( x , y ) after converting it to the frequency domain. Ḣ ( u , v ) is the blurring mask generated from the resulting image of the bilateral filter; T ( x , y ) is the blurred result of the bilateral filter by the BLP filter. Finally, it is worth mentioning that the boundary artifacts produced by the BLP filter are fixed by assigning the boundary values of the original image to the image produced by the BLP filter.

• C.    Unsharp Mask Filter

It is a famous yet simple sharpening filter, where its name originates from the fact that it improves edges and other fine details through a process which subtracts an unsharp (blurred) form of an image from the original image. This filter is commonly used in many imaging fields to increase the acutance of an image assumed to be blurred. The unsharp mask filter can be computed using the following equation [7]:

where, U ( x , y ) is the resulting sharp image; I ( x , y ) is the original blurry image; G ( x , y ) is image I ( x , y ) which is filtered by a Gaussian low-pass filter; k is a scaling constant, in which it should fulfill (k > 0), were larger values increase the amounts of the produced sharpness. In this article, the image smoothed by bilateral filter then blurred by the modified BLP filter is used within the unsharp mask filter to produce the final resulting image Q (x,y) as in the following equation:

Q ( x , y ) = I ( x , y ) + k [ I ( x , y ) - T ( x , y ) ] ^^

When using the traditional unsharp mask filter without the proposed modifications, the resulting image although clearer, maybe a less accurate representation of the image's subject. Thus, it is anticipated that the proposed filter would provide better performances than its traditional version in sharpening various images with poor acutance. In the forthcoming section, the results of different experiments with their discussions are given.

(e1)

(a1)                          (b1)                           (c1)                           (d1)

(a3)

Fig.2. Processing real-degraded images by the traditional and the proposed unsharp mask filters: (a1-e1) are original degraded images; (a2-e2) are images processed by the TUSM filter with k equal to (3, 2.5, 2.5, 2, 3) respectively; (a3-e3) are images processed by the proposed filter with k equal to (3, 2.5, 2.5, 2, 3) respectively.

• IV.    Results and Discussion

In this section, all the required information and discussions regarding the performed experiments, dataset of images, image quality assessment (IQA) metrics, and comparable filters, are provided. The dataset used in this study consists of various real and synthetic-degraded grayscale images that are collected from various free websites across the internet. Accordingly, the real-blurred images are used for experimental proposes, while the synthetic-blurred images are used for comparison purposes. The reason behind that is to know the true processing abilities of the proposed filter. For comparison purposes, the proposed filter is compared with the traditional unsharp mask filter (TUSM) [18], generalized unsharp mask filter (GUSM) [19] and Laplacian filter (LF) [20].

Regarding the used IQA metrics, two modern fullreference metrics are utilized namely, structural similarity (SSIM) [21] and visual information fidelity in the pixel domain (VIFP) [22]. Accordingly, the SSIM metric measures the quality according to the similarity in actual structures of a given image and its reference or recovered counterpart. In addition, the VIFP metric measures the quality according to the visibility of information of a given image and its reference or recovered counterpart. The output of the utilized metrics is a numerical value which is between 0 and 1, in which values near 1 indicate high visual quality for the assessed image, while values near 0 indicate the opposite.

It is important to mention that all implementations are achieved using MATLAB 2017a with a personal computer that has a 2.5 core I5 processor and 6 GB of memory. Fig. 2 demonstrates some of the attained experimental results with real-degraded images. Fig. 3 to Fig. 5 exhibit the results of the achieved comparisons between the proposed and the comparable filters. Table 1 shows the recorded accuracies of the achieved comparisons. Fig. 6 illustrates an analytical graph of the average scores in Tables 1.

Fig.3. Processing a synthetic-degraded image by the proposed and the comparable filters: (a) reference image; (b) reference image degraded by Gaussian blur with σ equal to 1; the rest of the images are processed by: (c) TUSM with k = 1.5; (d) LF; (e) GUSM; (f) proposed filter with k = 1.5.

(d)

(e)

(f)

Fig.4. Processing a synthetic-degraded image by the proposed and the comparable filters: (a) reference image; (b) reference image degraded by Gaussian blur with σ equal to 1.5; the rest of the images are processed by: (c) TUSM with k = 2; (d) LF; (e) GUSM; (f) proposed filter with k = 2.

^л<$й>м

(d)

(e)

'W^ . Ж

(f)

Fig.5. Processing a synthetic-degraded image by the proposed and the comparable filters: (a) reference image; (b) reference image degraded by Gaussian blur with σ equal to 2; the rest of the images are processed by: (c) TUSM with k = 2.5; (d) LF; (e) GUSM; (f) proposed filter with k = 2.5.

From the obtained results in Fig. 2, it can be seen that the proposed filter provided better results in terms of acutance and visibility of artifacts than the TUSM filter. The results of the TUSM filter exhibited an evident overshoot effect, while the results of the proposed filter showed realistic appearances without introducing the overshoot effect. Moreover, the obtained results by the proposed filter looked more natural, has adequate details with similar illumination to their degraded counterparts. This is significant because the proposed low-complexity modifications helped tremendously in preserving the original illumination of the processed image while improving the acutance.

From the obtained comparison results in Fig. 3 to Fig. 6, and Table 1, it can be seen the proposed filter performed very well in terms of IQA metrics and perceived quality, as it provided sharp results without introducing any unwanted artifacts. In addition, the performance of the TUSM filter was very near to the performance of the proposed filter, wherein the difference between the results of the two filters is slight and barely noticeable. As seen in Fig. 2, the difference between the two filters is somewhat noticeable, but when conducting the comparisons, it is barely noticeable.

The reason behind this is that the experimental images that are used in Fig. 2 are real-degraded images, in which their blurring model is unidentified. However, the comparison images are synthetic-degraded and their blurring model is known and is set to be Gaussian. Regarding the GUSM, it is evident that it produced well-sharpened edges, yet it noticeably modified the contrast of the processed images.

Table 1. The recorded accuracies of the achieved comparisons

#	Comparatives	Figures	SSIM	VIFP
1	Degraded	Fig. 3	0.8192	0.8639
		Fig. 4	0.6583	0.8400
		Fig. 5	0.5791	0.7122
		Average	0.6855	0.8053
2	TUSM	Fig. 3	0.8288	0.7864
		Fig. 4	0.6862	0.7778
		Fig. 5	0.7250	0.7289
		Average	0.7466	0.7643
3	LF	Fig. 3	0.7812	0.7658
		Fig. 4	0.6539	0.8136
		Fig. 5	0.6751	0.7710
		Average	0.7034	0.7834
4	GUSM	Fig. 3	0.7755	0.9409
		Fig. 4	0.6567	0.8102
		Fig. 5	0.6766	0.7472
		Average	0.7029	0.8327
5	Proposed filter	Fig. 3	0.8347	0.8741
		Fig. 4	0.6921	0.8476
		Fig. 5	0.7231	0.7570
		Average	0.7499	0.8262

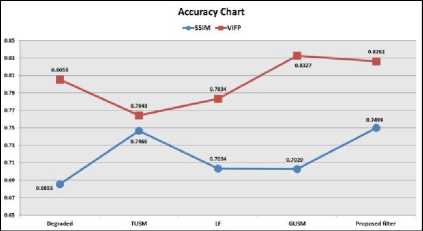
Fig.6. The analytical graph of the average scores in Tables 1.

This contrast modification can severely affect the quality of the recovered images, making them appear somewhat different than their original counterparts. This phenomenon is unacceptable in many real-world imaging applications. Regarding the Laplacian filter, it scored moderately in terms of IQA metrics. The proposed filter has many advantages, such as it owns a low structure, it produces results with no visible effects and it does not modify the contrast of the processed images. Developing an existing filter to produce results with less visible artifacts is a challenging task. However, this task is clearly achieved in this study, as the proposed filter produced visually pleasing results with natural contrast and acceptable brightness.

• V.    Conclusion

In this article, an amended unsharp mask filter for sharpening digital images is introduced. The proposed filter uses the traditional bilateral filter and a modified Butterworth filter to soften the image instead of using the Gaussian low-pass filter only as in the TUSM filter. This approach helped tremendously in avoiding the generation of the overshoot effect while providing acceptable results. The proposed filter is benchmarked with synthetic and real-degraded images and is compared with the three famous image sharpening filters. Furthermore, the accuracy of the obtained results is measured using two well-known metrics of SSIM and VIFP. From the obtained results, it can be seen the proposed filter provided satisfying results and outperformed the comparable filters, in which it performed very well in terms of visual quality and IQA metrics. Accordingly, the proposed filter provided results that have a natural appearance and no visible artifacts. Such acceptable results can highly support the validity of the developed filter. Finally, the use of low-complexity methods for image sharpening is desirable in many existing systems, especially those with minimal resources.

Acknowledgment

The authors state that they have no conflict of interests regarding this work.