Импульсная терагерцовая голография с разрешением во времени в дисперсионных средах

В последние несколько лет системы ТГц-спект-роскопии нашли своё применение в таких областях, как биология и медицина [1 –3], охранные системы [4], фармакология [5], неразрушающий контроль [6]. Отдельным большим пластом применений ТГц-излучения являются методы формирования изображения. Актуальность использования ТГц-диапазона для этих целей обусловливается следующими параметрами: высокая проникающая способность; длина волны ТГц-излучения позволяет получать изображения с субмиллиметровым разрешением, широкая полоса частот в пределах от 100 ГГц до 10 ТГц обеспечивает возможность производить спектроскопические измерения образцов, чьи спектральные особенности лежат в этом диапазоне. К таким объектам относятся многие взрывчатые вещества, органические молекулы и сложные полимеры. Также ТГц-излучение характеризуется низкой энергией фотонов, что обуславливает его неионизирующий характер, позволяя использовать его в медицине. При прямом детектировании временной зависимости напряженности электрического поля ТГц-излучения возможно получение комплексных спектров, таким образом, регистрируя полную информацию об амплитуде и фазе прошедшей или отражённой от образца волны.

Формирование изображения, визуализация внутренней структуры объектов, неразрушающий контроль изделий, томография и голография в ТГц-диа-пазоне частот представляют значительный интерес как для научных, так и для практических применений [7, 8]. В настоящее время в ТГц-оптике большое внимание уделяется задаче измерения фазовых характеристик ТГц-поля, а также трёхмерных геометрических характеристик сложных фазовых объектов с пространственным и/или частотным распределением показателя преломления в ТГц-диапазоне. Также ТГц-излучение используется для получения полного трёхмерного изображения объектов [9 – 13], в том числе скрытых внутри дисперсионных сред.

Импульсная ТГц-голография с разрешением во времени [14] представляет собой перспективный метод измерения фазовых характеристик ТГц-поля. Эта техника обладает рядом существенных преимуществ по сравнению с ТГц-спектроскопией с разрешением во времени, так как предполагает измерения в коллимированном пучке, что буквально означает, что объект может быть стационарно расположен в любом месте внутри него, что часто требуется при проведении измерений в реальном времени. Вдобавок для практической реализации измерений требуется минимальное количество оптических элементов ТГц-диапазона, поскольку регистрация поля производится сканирующей диафрагмой или матрицей фотодетекторов в широкоапертурном коллимированном пучке, прошедшем через объект. При такой конфигурации качество восстановления не зависит от оптики, используемой в установке. И что самое важное, достижимое разрешение, которое сопоставимо с длиной волны [15], значительно выше, чем у конкурирующей техники ТГц-спектроскопии с разрешением во времени [16], где разрешение ограничено размером перетяжки пучка.

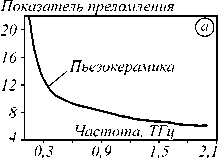
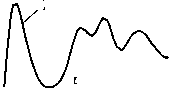
Метод импульсной терагерцовой голографии предполагает регистрацию данных рассеянного объектом широкополосного излучения в зоне дифракции с последующим численным решением уравнения распространения волн для пространственного распределения комплексной амплитуды на каждой из спектральных компонент [14]. Во всех предыдущих работах по данной тематике [17–20] рассматривалось распространение волн в среде с пренебрежимо малой дисперсией или без неё. В то же время на практике часто встречаются материалы, обладающие характерной зависимостью показателя преломления от частоты. На рис. 1 представлены неко- торые из таких сред из числа актуальных и часто встречающихся в литературе по исследованиям в ТГц–тематике. Стоит отметить, что проблема дисперсии среды может также возникать в случае сложных слоистых объектов или объектов, скрытых внутри других.

Показатель преломления

1,50--------------------

1.48

1.46

1,44

1,42

1,40

Ткань мозга .мыши

0,4       1,2        2.0

Частота, ТП;

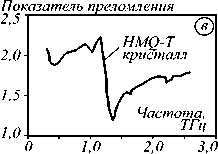
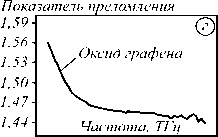
Рис. 1. Дисперсия показателя преломления: в пьезокерамике [21] (а), ткани мозга мыши с болезнью Альцгеймера [22] (б), HMQ-T кристалле в направлении оси А [23] (в), восстановленном оксиде графена [24] (г)

0.5 1,0 1,5 2,0 2,5 3,0

В данной работе мы адаптируем модель голографического восстановления изображения объекта, основанную на математическом аппарате скалярной теории дифракции для случая распространения волнового поля в дисперсионной среде, в которую помещён исследуемый объект, а также показываем влияние учёта дисперсии среды на восстановление фазовых характеристик и рельефа объекта на этапах записи и восстановления голограммы. Таким образом расширяется класс задач, связанных с восстановлением изображений объектов.

1.    Предложенная математическая модель

В работе [14] была предложена математическая модель записи и восстановления голограммы, которая осуществляется по методу ТГц импульсной голографии с разрешением во времени с использованием численного расчёта распространения волнового фронта в пространстве, основанная на алгоритмах представления поля через угловой спектр плоских волн (УС):

u(x, y,l) = JJ' U(fx, fy)exp[2лi(fxx + fyy)]x xexp[(2niAl / X)^1 - (fx)2 - (fy )2 ] dfxdfy, где fx, fy – пространственные частоты, получаемые при разложении в двумерный Фурье-спектр, λ – длина волны, Δl – расстояние, для которого производится численный расчёт распространения.

Метод свёртки поля с импульсным откликом системы (С) определяется выражением:

U (x, y, l) = u (x', y', 0) ® h (x, y, l),(2)

где h – импульсный отклик системы:

h (x, y, l) = (exp [2n ir/X] / i X r) (l / r)(3)

и r – расстояние между выбранной точкой на объектной плоскости и плоскости регистрации:

r = V12 (x-x’)2 +(y- y ’)2 .(4)

В формулах (1), (2) предполагается модель, при которой показатель преломления постоянный и равен 1. Для расчёта как дифракционных картин, отражающих получаемые в эксперименте данные [25], так и для восстановления по этим данным амплитуднофазовых характеристик объекта, представленные уравнения решаются для всех частот рассматриваемого нами ТГц-диапазона (0,5–2,0 ТГц). Согласно определению, дисперсия есть зависимость показателя преломления среды от частоты. При распространении широкополосного цуга электромагнитных волн в дисперсионных средах наблюдается различие фазовых скоростей в зависимости от их частоты. В работе [25] показано влияние длины волны на пространственные частоты дифрагированного на объекте излучения. Для учёта дисперсии показателя преломления в нашей математической модели распространения волнового фронта уравнения для метода УС дополнены функцией (n(λ)):

u(x, y, l) = J J-^ U(fx, fy) exp[2ni(fxx + fyy)]x xexp[(2niAl / Xn(X))^1 - (fx)2 - (fy)2 ] dfxdfy и аналогично для метода С:

U (x, y, l) = u (x ’, y ',0) ® h'(x, y, l), где h'(x, y, l) = (exp [2n ir/X n (X)] / i X r) (l / r).

Область применения методов углового спектра и свертки с учётом дисперсии среды определяется неравенством:

v>v ₀ = cl / n ( X ) N A x 2 ,

где ν – частота, c – скорость света, N – количество пикселей в дискретном представлении поля, Δ x – размер пикселя.

Формула (8) устанавливает соотношение между частотой излучения и расстоянием l . Согласно этому неравенству, при v ≥ v 0 используется метод УС, а при v <  v ₀ - метод С.

Расчёт распространения поля проводился для случаев без учёта дисперсии среды, с учётом дисперсии только при записи голограммы и с учётом дисперсии при записи и восстановлении. Под терминами «запись голограммы» и «восстановление голограммы» мы подразумеваем численный расчёт распространения волнового поля из плоскости объекта в плоскость голограммы и из плоскости голограммы в плоскость объекта соответственно. В реальном эксперименте голограмма представляет собой поле, зарегистрированное после прохождения амплитудно-фазового объекта на определённом расстоянии l, в той плоско- сти, где располагается растровая сканирующая диафрагма (рис. 2, увеличенный фрагмент). В эксперименте мы имеем возможность получить распределение терагерцового поля только в плоскости голограммы (что равносильно термину плоскость регистрации). Соответственно, результаты численного моделирования с учётом дисперсии только при записи голограммы являются отражением проблемы, возникающей в реальном эксперименте, а именно: при распространении поля после прохождения объекта в плоскость регистрации происходит дополнительный фазовый набег в дисперсионной среде, и неучёт этой дисперсии при дальнейшей численной обработке результатов приводит к значительным искажениям в восстанавливаемом изображении.

В данной работе рассматривается случай поиска скрытого объекта в мозговой ткани мыши с болезнью Альцгеймера, которая обладает дисперсией в диапазоне 0,5 –2,0 ТГц (рис. 1 б ). Проводимое нами математическое моделирование является компьютерной симуляцией эксперимента по записи и восстановлению импульсных ТГц-голограмм по схеме, описан-

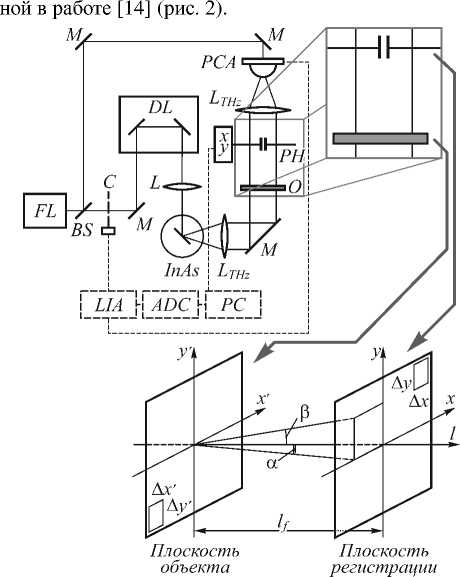
Рис. 2. Принципиальная схема численного моделирования.

Увеличенный фрагмент демонстрирует объект исследования (О) и диафрагму (РН), которые в предложенной численной модели представляют собой плоскость объекта и плоскость регистрации

соответственно

2.    Результаты численного моделирования

Для моделирования записи и восстановления тера-герцовых голограмм в приближении тонкого транспаранта были использованы амплитудная (распределение Гаусса, рис. 3а) и фазовая («фазовый конь», рис. 3б) маски исследуемого объекта, а также смоделирован идеальный однопериодный импульс, представляющий собой одно колебание электрического поля длительностью порядка 2 пикосекунды с шириной спектральной полосы до 2,5 ТГц (рис. 3в). Также на рис. 3 показаны распределения фазы сразу после объекта на разных частотах ТГц-спектра.

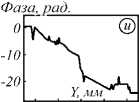
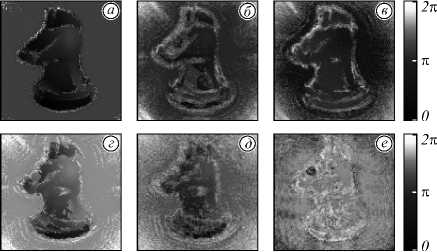
После моделирования записи и восстановления голограммы были получены пространственно-частотные распределения фазы в плоскости объекта. Для корректной оценки фазовых изображений был применён стандартный алгоритм развёртки фазы по спектральной частоте. На рис. 4 показаны фазовые портреты восстановленных голограмм на отдельных частотах ТГц-спектра для случаев учёта дисперсии при записи и восстановлении (рис. 4 а-в ) и для случаев учёта дисперсии показателя преломления только при записи (рис. 4 г-е ).

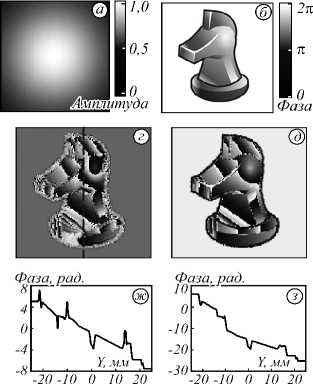
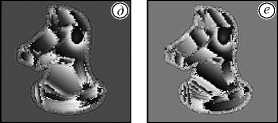
Рис. 3. Начальное распределение амплитуды (a) и фазы (б) объекта, используемый в моделировании ТГц-спектр (в), распределение фазы сразу после объекта на частоте 1 ТГц (г), распределение фазы сразу после объекта на частоте 1,5 ТГц (д), распределение фазы сразу после объекта на частоте 2 ТГц (е). Cечения фазового изображения (ж–и) – для случаев (г–е) соответственно

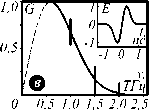
-20-10 0 10 20

При сравнении изображений на одинаковых частотах отчётливо видна разница в пространственном распределении фазовых характеристик, вызванная дополнительным фазовым набегом в среде при распространении поля.

Механизм появления ошибок в случае, если дисперсия среды имеет место, а в математическом моделировании восстановления голограммы она не учитывается, следующий: при распространении назад в случае, если показатель преломления среды зависит от частоты излучения, происходит смещение плоскости численной фокусировки для каждой из компонент широкого спектра, и величина этого смещения зависит от характера кривой дисперсии. Если закон дисперсии линейный, то смещение плоскости численной фокусировки будет эквидистантным. В общем виде характер смещения этой плоскости зависит от производной дисперсионной кривой.

Фаза, рад.

-20-10 0 10 20

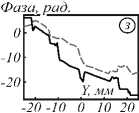
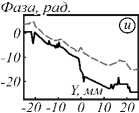
Рис. 4. Восстановленные фазовые изображения: с учетом дисперсии среды (a–в) и без учёта дисперсии на различных частотах в ТГц диапазоне (г–е). – Cечения поверхностей (ж–и): сплошная линия для случаев (a–в) и пунктирная линия – для случаев (г–е). Рисунок (ж) иллюстрирует случай, при котором для выбранной спектральной компоненты (1 ТГц) набег фазы совпадает

При сравнении фазовых портретов с теми, которые формировались непосредственно сразу за объектом (рис. 3г-е), стоит отметить, что для случая полного учёта дисперсии в обоих направлениях распространения поля фазовые характеристики совпадают для всех частот спектра, что объясняется компенсацией фазового набега при распространении в среде на расстояние l обратным фазовым набегом при распространении назад в плоскость объекта на расстояние –l. При этом неучёт дисперсии среды при восстановле- нии голограммы приводит к некорректному восстановлению исходных фазовых характеристик поля, что приводит к искажению получаемого изображения и к ошибке в расчёте рельефа, поскольку для перехода от фазы поля на всех частотах к профилю объекта необходимо считать суммарную картину на всех длинах волн. Рельеф структуры в случае, когда объект состоит из однородного материала, будет иметь вид:

∆ϕ ( x ₀, y ₀, λ _i ) λ _i 2 π ( n - 1)

1 I   m-Л

h ⁽ x 0 , У 0 ) = — I E m I < = i

где Δφ – значение фазы поля в точке объекта для каждой длины волны, ( x 0 , y 0 ) – координаты, c – скорость света, n – показатель преломления объекта.

Если анализировать поведение фазы во всей рассматриваемой нами частотной области в одной из произвольно выбранных точек объекта (рис. 4 а ), то здесь также усматривается изменение динамики фазового набега при восстановлении голограммы без учёта дисперсии среды, поскольку в зависимости фазы от частоты для каждой спектральной компоненты появляется свой коэффициент угла наклона фазы, вызванный дисперсией среды.

Если перейти от фазовых характеристик для всей частотной области к рельефу (уравнение 9), то неучёт дисперсии при восстановлении приводит к появлению флуктуаций рельефа на частотной шкале, что является очевидно некорректным, поскольку параметр высоты объекта в точке не зависит от длины волны излучения, с помощью которой этот рельеф восстанавливается (рис. 5б).

На рис. 5 учёт дисперсии (УД) и неучёт дисперсии (БД) даёт одинаковый результат при численном моделировании расчёта записи и обратного восстановления голограммы, что подтверждает правильность предложенной модели: случай, дополненный дисперсией, даёт дополнительный набег фазы при распространении вперёд и обратный набег фазы при последующем распространении назад в среде.

Следовательно, дополнительные фазовые набеги корректно компенсируются при распространении вперёд и затем назад, что не противоречит более простой модели без дисперсии вообще. Однако, если не учитывать дисперсию при восстановлении голограммы при её наличии при записи, то будет накапливаться ошибка. Это является важным обстоятельством, так как в реальном эксперименте дисперсия при записи голограммы присутствует априори, и при последующей численной обработке отказ от её рассмотрения приводит к ошибке в восстановлении изображения и рельефа.

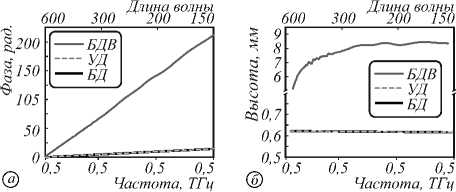
Рис. 5. Восстановленные характеристики объекта в точке: изменения в фазовом запаздывании в точке изображения с координатами (х = 5, y = 25) (а); зависимость рельефа объекта в частотном диапазоне в точке с координатами (х = 5, y = 25) (б). Обозначения: УД – с учётом дисперсии при записи и восстановлении изображения, БД – без учёта дисперсии при записи и восстановлении изображения, БДВ – без учёта дисперсии только при восстановлении изображения

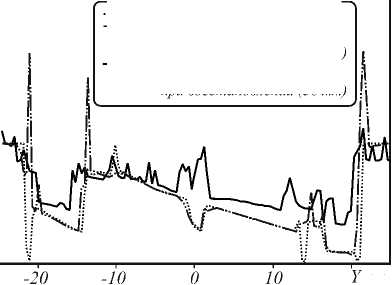
При расчёте рельефа с учётом суммирования по всей частотной области ошибка будет проявляться в виде отклонений функции рельефа восстановленного объекта от эталонного. При этом примечательно, что при увеличении расстояния l между плоскостью объекта и плоскостью голограммы происходит накопление ошибки, поскольку такое увеличение расстояния по сути подразумевает увеличение длины дисперсионной среды. На рис. 6 приведён суммарный по всему спектру восстановленный рельеф объекта для обсуждаемых в работе случаев.

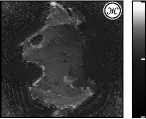
Процесс накопления ошибки в восстановлении изображения объекта визуализирован на рис. 7, показывающем рост искажений при увеличении расстояния до плоскости голограммы. Также приведены значения нормального среднеквадратичного отклонения (НСКО), рассчитанные по формуле:

E ²

El g ( x ^, y ) - f ( x ^, y )| 2

El f ( x ^, y )| 2

где g ( x , y ) и f ( x , y ) – суммарные фазовые изображения для восстановленного и эталонного объекта соответственно. НСКО возрастает от 0,30 до 0,45 по мере увеличения расчётного расстояния распространения.

Высота, мм 3,0---------

2,5-

2,0-

1,5-

1,0-

0,5-

Y мм

............Рельеф исходного объекта

----Рельеф объекта без учёта дисперсии при' восстановлении (10 мм)

-----Рельеф объекта без учёта дисперсиг!

при восстановлении (50 мм)

Рис. 6. Сечения поверхности восстановленного объекта: точечная линия – эталонный рельеф тест-объекта; штрихпунктирная линия – восстановленный рельеф без учёта дисперсии при восстановлении на расстоянии l = 10 мм; сплошная линия – восстановленный рельеф без учёта дисперсии при восстановлении на расстоянии l = 50 мм

0,48

0.44

0.40

0.36

0.32

0,28

10 20 30 40 50 60 70 80

Рис. 7. Восстановленные суммарные изображения

на различных расстояниях численного распространения: 10 мм (а), 20 мм (б), 30 мм (в), 40 мм (г), 50 мм (д), 60 мм (е), 70 мм (ж). Возрастание НСКО восстанавливаемых изображений относительно эталонного при неучёте дисперсии среды распространения (з)

Заключение

В данной работе мы представили модель, учитывающую дисперсию среды, и показали в численном моделировании, как рассмотрение зависимости показателя преломления среды от частоты импульсного широкополосного терагерцового излучения влияет на процесс восстановления рельефа и изображения исследуемого тест-объекта.

Представленные уравнения численного расчёта распространения волнового фронта в дисперcионных средах также могут быть полезны не только для задач интравидения в терагерцовом диапазоне частот, но и для расчёта дифракции как широкополосного, так и монохроматического излучения, например, из видимого диапазона частот, в средах с показателем преломления n ≠ 1 [26, 27]. В таком контексте использование полученных результатов приобретает дополнительную значимость для задач цифровой низкокогерентной голографической микроскопии [28], оптической когерентной томографии [29], а также нелинейной оптики, например, для исследования особенностей распространения лазерного излучения в оптически нелинейных средах [30, 31] и др.

Работа выполнена при поддержке правительства Российской Федерации, гранты 3.1893.2017/ПЧ и 074-U01.