Импульсное возбуждение гармонического осциллятора: зависимость от параметров возбуждающей силы

Развитие технологии генерации импульсных источников волн различной природы (электромагнитных, акустических и др.) с заданными параметрами (длительностью, несущей частотой и формой огибающей) делает актуальным исследование особенностей и специфических черт их взаимодействия с веществом. Важной моделью для описания этого взаимодействия как в классической, так и в квантовой физике является гармонический осциллятор.

• (с) Астапенко В. А., Кротов Ю. А., Сахпо С. В., 2023

2.    Классический осциллятор

Это обусловлено как минимум двумя обстоятельствами. С одной стороны, данная модель применима к широкому кругу объектов при их относительно слабом возмущении. С другой стороны, в квантовой физике динамика гармонического осциллятора может быть описана точно при любой силе воздействия [1]. Здесь стоит отметить важную связь, которую осуществляет классический осциллятор при описании явлений в квантовой и классической физике. Эта связь проявляется в известном принципе спектроскопического соответствия [2], а также в том, что динамика квантового осциллятора определяется ассоциированным с ним классическим осциллятором [3]. Еще одним важным обстоятельством является то, что использование осцилляторной модели позволяет в ряде случаев упростить задачу, выявив при этом основные существенные черты исследуемого явления.

Настоящая статья посвящена исследованию зависимости энергии возбуждения классического осциллятора с затуханием под действием импульса периодической силы различной длительности от параметров импульса, включая форму огибающей, за все время его действия.

Рассмотрим возбуждение гармонического осциллятора с затуханием под действием импульса периодической силы с частотой, близкой к собственной частоте осциллятора. Соответствующее уравнение имеет вид

Ж + 2₇Ж + —2® = М / (t,T,We),                           (1)

где F q - амплитуда силы, М - масса осциллятора, у - константа затухания, / (t, т, —_с) - безразмерный временной профиль силы, т - длительность импульса, —_с - несущая частота силы, которая предполагается близкой к собственной частоте осциллятора — q.

Энергия возбуждения осциллятора за все время действия импульса определяется равенством

А е ( т, -_с) = А = Ғ о / J(t,T,^c)±(t)dt,                            (2)

где А - работа силы над осциллятором.

Для дальнейшего удобно выразить энергию возбуждения через безразмерную величину АДт, —_с) в соответствии с формулой

²У^{— 2 | j ( -,т,-} с ^)|2  ,

(-2 - -2)2 +4у2—2

Здесь / (—,т,—_с) - фурье-образ от временного профиля силы на частоте —.

В дальнейшем предполагаем, что выполняется неравенство — о >> у (осциллятор имеет высокую добротность), тогда из (4) следует приближенное выражение

А е ( т,—_с ) = — Г               d- = ^ Г L(—,—o,y )IJ(-,т,-с)І^-,      (5)

2т Jo (- - -о)2 + у2       2 Jq где

L(-,-o,y) =

У^/т (- - - о ) ² + у²

• - лоренциан, который, в частности, описывает форму спектральной линии при однородном уширении излучательного перехода.

Рассмотрим далее две огибающие импульса силы: экспоненциальную и гауссовскую.

Экспоненциальный импульс

Экспоненциальный импульс определяется выражением

J ep (t,т ) = e(t)exp(-t/T )cos(wct),

где 6(t) - функция Хэвисайда. Соответствующий квадрат модуля фурье-образа в приближении вращающейся волны (ш_ст >>  1) имеет вид

1         т ²

^{| J ep} (_Ш,^т,Ш^с)| = 4 1 + _(ш - _Шс)2т ² •

После подстановки (8) в (5) и вычисления интеграла находим

Г 2      (7 ^{+ т} 1) ^/г

^{АеЕР (т Шс)} = 8 ^Ш0^т (Шс - Шо)² + (7 + т -1)2 ■                      ⁽⁹⁾

Таким образом, в рассматриваемом случае спектральный профиль (9) описывается ло-ренцианом с шириной

А ш ер = 7 + т 1.

(Ю)

(И)

В пределе ультракоротких импульсов т << 1/7 из (9) получаем д ~         _ 1      Ш0т2

^А ^ ^{ер (т,Шс)}   ₈(шс - Шо)2т² + 1.

Отсюда, в частности, следует квадратичный рост энергии возбуждения с длительностью импульса, если (ш_с - Шо)2т ²< 1.

В противоположном, квазимонохроматическом, пределе (7т >> 1) из (9) имеем

^А ер (т-хШс) = 8-Щт (_Ш - _Ш 7 ) _{2 + 7} 2 = | ш2^тЦшс,шо,7)-              (12)

Таким образом, в этом случае энергия возбуждения является линейной функцией длительности импульса силы.

Как следует из (9), поглощенная энергия под действием экспоненциального импульса силы является монотонной функцией длительности т, квадратично возрастающей при малых длительностях и линейно возрастающей в пределе длинных импульсов. Соответствующие зависимости представлены на рис. 1, для различных отстроек несущей частоты силы от собственной частоты осциллятора.

Точка перегиба на приведенных зависимостях дается выражением, следующим из формулы (9):

т *

V3|шс - Шо| - 7

Таким образом, перегиб функции А ё ер (т ) существует, если выполняется неравенство

|Шс - Шо| > 7/ V3,

т.е. при достаточно больших частотных отстройках.

Как видно из рис. 1 с увеличением частотной отстройки растет ширина области параметра т с центром в точке перегиба, в которой энергия возбуждения слабо зависит от длительности импульса.

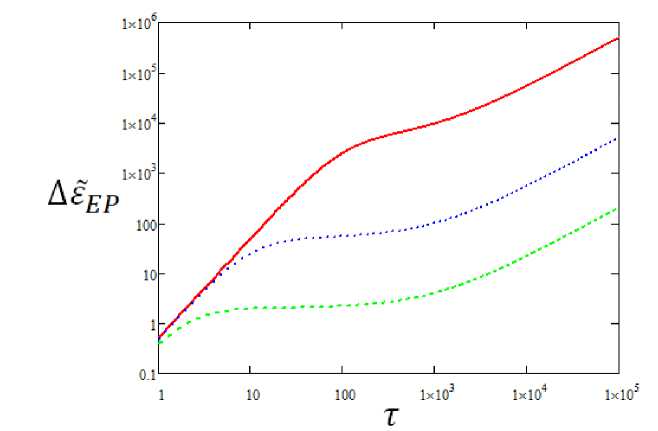
Рис. 1. Зависимость энергии возбуждения гармонического осциллятора, под действием силы с экспоненциальной огибающей для различных отстроек Аш несущей частоты силы от собственной частоты осциллятора: сплошная линия - Аш = 0.01 оти. ед., пунктир - Аш = 0.1 оти. ед., штриховая линия - Аш = 0.5 оти. ед., шо = 2 от и. ед., у = 0.001 оти. ед.

Гауссовский импульс

Гауссовский импульс определяется следующим временным профилем:

fG(t,т) = exp(—t2/2т 2)cos(шct),(15)

квадрат модуля фурье-образа которого в приближении вращающейся ( ш_ст >>  1) волны равен

|/е(ш,т,шс)|2 = |T2 exp(—(ш - шс)2т2).(16)

Подстановка. (16) в формулу (5) и вычисление возникающего интеграла, дает

Аёс(т, шс) = ш0т2Re{w[(wo - шс)т + гут]},(17)

где w(z) = exp(— z²)erf c(—iz) - комплексная функция ошибок, erf c(x^) - дополнительная функция ошибок.

Из формулы (17) следует, что спектральный профиль в данном случае описывается контуром Фойгта [5] со спектральными ширинами Аше = 1/т, Аш^ = у.

В квазимонохроматическом пределе ( ут >>  1) из (17) вытекает линейная зависимость энергии возбуждения от длительности импульса по аналогии с формулой (12):

Аё_с(т,шс = шо) та —0—.                             (18)

УМ^

На рис. 2 представлена, энергия возбуждения осциллятора, как функция длительности гауссовского импульса, рассчитанная по формуле (17), для различных отстроек несущей частоты.

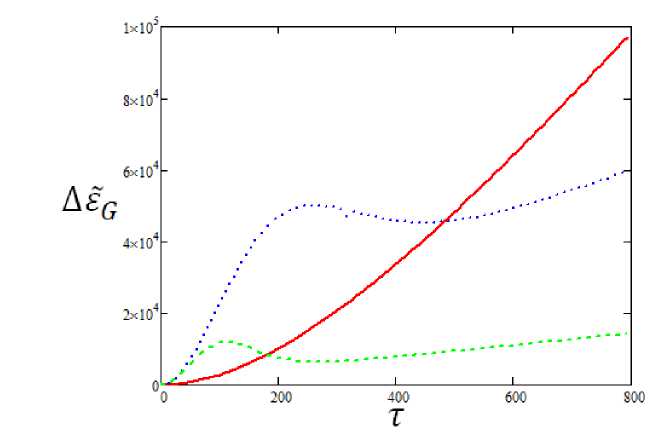
Рис. 2. Зависимость энергии возбуждения гармонического осциллятора, под действием силы с гауссовской огибающей для различных отстроек Аш несущей частоты силы от собственной частоты осциллятора: сплошная линия - Аш = 0, нуиктир - Аш = 0.005 оти. ед., штриховая линия - Аш = 0.01 оти. ед., шо = 2 от и. ед., у = 0.001 оти. ед. Ордината сплошной кривой уменьшена в 10 раз

Существенное отличие приведенных на. данном рисунке кривых от графиков рис. 1 заключается в том, что в случае достаточно больших отстроек имеют место экстремумы функции Аё(т ). Можно сказать, что при переходе от экспоненциального импульса к гауссовскому точка, перегиба, в данной функции преобразуется в экстремумы (максимум и минимум). Положение максимума, можно описать приближенным равенством

^T max ~ 1 ^|ш с ^—

На резонансной несущей частоте энергия возбуждения сначала, растет квадратично с ростом т, а затем линейно при больших длительностях (18).

Отметим, что выражения, аналогичные (9) и (17), были получены в статье [6] при исследовании временной зависимости резонансных фотопроцессов в поле лазерных импульсов различной длительности в рамках квантово-механического подхода.

3.    Квантовый осциллятор

Рассмотрим возбуждение квантового осциллятора, из m-го стационарного состояния под действием той же силы, что и в случае классического осциллятора. Классическая сила, переводит квантовый осциллятор из стационарного в когерентное состояние |д) (z - параметр когерентного состояния). Поэтому квантовое число п конечного стационарного состояния не фиксировано, а дается распределением W_mn (W_mn ~ вероятность возбуждения осциллятора на переходе ттг ^ п). В работе [3] было показано (см. также [7]), что среднее квантовое число п в результате возбуждения осциллятора выражается через работу возбуждающей силы А согласно формуле

А п = ттг + -—. ашо

С учетом (3) отсюда, находим

п = ттг +

F0

М Пш3

Ае(т, ш_с).

Таким образом, среднее число квантов осциллятора после возбуждения определяется безразмерной функцией Аё(т, ш_с), для которой справедливы все результаты предыдущего раздела. Заметим, что величина п^шо равна средней энергии квантового осциллятора после возбуждения. Любопытно отметить, что эта энергия пропорциональна квадрату амплитуды возбуждающей силы, в то время как вероятность возбуждения, например, на переходе 0 ^ п пропорциональна Ғц^п, как это следует из общей формулы для вероятности, полученной впервые в статье [1].

Среднее значение оператора координаты квантового осциллятора Q в когерентном состоянии на временах, меньших времени затухания ( t <  1/у), равно

Q =² \Bz?

V 2М Ш о

| z | cos(wot — arg z),

причем

| ^ | = Vn.

Поскольку величина п дается формулой (21), то амплитуда колебаний среднего от оператора координаты квантового осциллятора также определяется функцией Ае(т,ш_с)

4.    Заключение

В работе теоретически исследована зависимость энергии возбуждения гармонического осциллятора с затуханием от параметров импульса околорезонансной возбуждающей силы за все время действия силы. Рассмотрены две формы огибающей импульса: экспоненциальная и гауссовская.

Получены простые выражения, описывающие энергию возбуждения классического осциллятора как функцию длительности и несущей частоты силы в обоих случаях. Рассмотрены пределы ультракоротких и квазимонохроматических импульсов.

Установлено, что при достаточно больших отстройках несущей частоты импульса от собственной частоты осциллятора зависимость энергии возбуждения от длительности импульса имеет точку перегиба в случае экспоненциальной огибающей и экстремумы (максимум и минимум) - в случае гауссовской огибающей.

Показано, что средняя энергия возбуждения квантового осциллятора и средняя амплитуда его колебаний определяются той же зависимостью от параметров возбуждающей силы, что и в случае классического осциллятора.

Работа выполнена при поддержке Министерства науки и высшего образования Российской Федерации в рамках государственного задания (договор 075-03-2023-106 от 13.01.2023).