Incommensurate magnetic structure in an antiferromagnet with a strong exchange interaction between delocalized and localized electrons

The formation of incommensurate structures has often been observed in low-dimensional systems with spin, such as RbCuCl 3 [1], and in the field-induced lattice of magnetic solitons in spin-Peierls compounds CuGeO 3 [2]. The reason for the formation of incommensurability is the competition of various interactions: antiferromagnetic exchanges between near and nearest neighbors [3], Dzyaloshinsky – Moriah interactions and the interaction between magnetic systems and elastic [4] or electronic systems [5] with an incommensurate period of the structure. An incommensurate structure in a three-dimensional ordered magnetic lattice was found in CuB 2 O 4 [6]. With a decrease in temperature, a second magnetic phase transition occurs in the direction of an incommensurate threedimensional magnetic order. In an incommensurate phase, but nearby, satellites of a higher order appear on the neutron diffraction pattern. CuB 2 O 4 crystallizes in the space group with lattice constants a = 11.528 Å and c = 5.607 Å [7]. The existence of such a magnetic structure has been explained by relativistic effects such as spin-orbit interaction, which is attributed to a kind of the Dzyaloshinsky - Moria (DM) interaction. Using the DM interaction and anisotropy in the basal plane, the modulation of the order parameter in copper metaborate along the direction of the spiral is described in the framework of the Landau theory of phase transitions by solving the sine - Gordon equation. The magnetic structure changes as a result of interaction with the elastic subsystem [8; 9]. The interaction of spins with optical [10] and acoustic [11] vibration modes leads to a decrease in the magnetization and, at some critical parameters, to the disappearance of the long-range magnetic order [12; 13]. An increase in the magnetic anisotropy field as a result of four-spin exchange is also possible [14; 15].

The paper considers the interaction of two subsystems: a magnetic one and an electronic one. Depending on the magnitude of the interaction between current carriers and localized spins, it is necessary to consider new quasiparticles - spin polarons. In this case, the formation of an incommensurate magnetic structure is possible. The paper proposes a microscopic theory of the formation of an incommensurate magnetic structure in CuB 2 O 4 .

Model

CuB 2 O 4 exhibits weak piezoelectric properties [16]. Thus, uniaxial pressure along [011] causes electrical induction. The velocity of acoustic transverse waves propagating along [100] is anisotropic for wave polarization, [010] and [001] [16]. These results indicate the existence of anisotropy of the electron density distribution within ~ 8 %.

It can be assumed that the electrical properties of copper metaborate are due to the bound states of electrons and holes. The difference between the ionization energies of copper and boron ions Cu2+, B3+ is Д(E 3 + -E 2+ )-1 эВ [17], and they are linked by a covalent bond through oxygen. The disB"'      Cu- +/ placement of the electron density on the covalent bond can increase the effective charge of copper and decrease the charge of boron. This fast can be interpreted as the formation of a hole in the copper ion. The strong interaction of holes with excitations of the antiferromagnetically ordered spin subsystem is described within the s – d model. In this case, a more complex excitation, a spin polaron, is a good quasiparticle.

Let us define low-lying spin-polaron states using the mean-field approximation in the Kondo lattice model [18]. The Hamiltonian has the following form:

H = H ₀ + H 1 + H ₂,

H 0 = l ( t h p a r+ h_p ,. a r ,. ⁺ t h c a r+ h_c ,. a r ,. ⁺ ec - ) = Z ^S k a ⁺ ,. a k .a ,                   ⁽¹⁾

r , g                                                             k

H1 = J Z ar,4 Sr.°P2 ar,.2 , r,01,^2

H 2 = 2 1 Z S r+g S a .

f , g

Here the nodes r form a tetragonal lattice; hp and h are the distances to the nearest neighbors in the plane and along the c axis; ak . is the operator of creation of holes with spin indices . = ±1; Ho describes the hopping of charge carriers; th = -tr; tb = -10 ; H2 is the antiferromagnetic interaction pc of localized spins S = 1/2 with their nearest neighbors; H1 is the Hamiltonian of local Kondo interaction; .a is Pauli matrices and a = x, y, z .

Let us write the first two equations for the Green's functions describing the motion of a hole against an antiferromagnetic background. Using the random phase approximation, a system of equations for the Green's functions ^ a _r . | a ¹ .^^ and ^^ b _r .| a r .^^ , b _r . = S _r ^a. .. a _r . , a = x,y is closed. These equations are as follows:

^{( m  s} k ) G k = ¹ + — G k ,

( ®- e _k ) G k = J ( 1 + m - 2 nm ) G k , ^G k =^ ( a k ,a| a k,a) ^        ^G k =^ ( b k ,a| a k,.}^

ek = ek + ~ - ц,                                              (2)

s k = - 2 1 1 ( cos k_x + cos k_y ) - 2 1 ₀ cos k_z, n о . г Г m Y ^z т

ek = 2 zce. + J — + n + — ml - ц, k       k ^ 2 J 2

n = [ a I a^ + a J a^ \.

Here, b , a and G are the Fourier transforms of the corresponding local operators and Green's functions, respectively; c = SSSS_{x+ g} + S_r^yS_r^y _+g ^ is the spin-spin correlation function on the transverse components of the spin; z is the number of nearest neighbors; m is the magnetization of the sublattice. All energies are measured from the chemical potential ц .

The solution of the system of equations (2) leads to the following spectrum of excitations:

® 1,2 ^{( k} ) = ¹

Sk

⁺ e k ±J (^S k

x 2   r2 Г1 + m

- ek) + J I--nm

The chemical potential is calculated from the self-consistent solution of the equation for the hole concentration n n=-1 Ef dю f (ю) 1Im G1,                          (4)

where f ( ю ) = ( exp ( ra / T ) + 1 ) ¹. The summation over the momentum in the Brillouin zone is performed using 8 × 10⁶ dots.

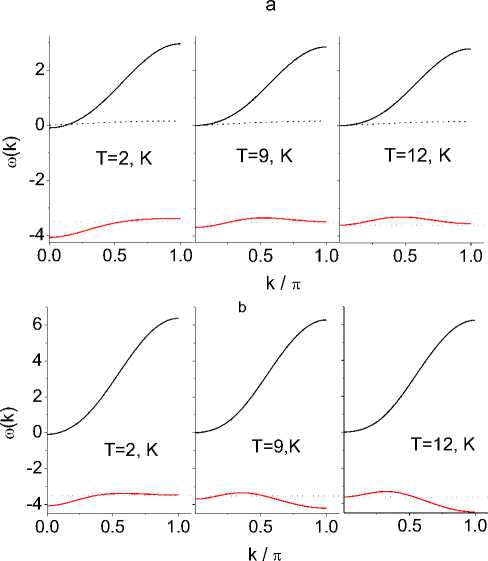
0.0     0.5     1.0       0.5     1.0       0.5     1.0

k / n

Fig. 1. Dispersion branches of spin-polaron excitations along [001] ( a );

[101] ( b ); [111] ( c ) at different temperatures. The horizontal line indicates the position of the chemical potential in the lower bar (dashed line)

Рис. 1. Дисперсионные ветви спин-поляронных возбуждений вдоль [001] ( а );

[101] ( b ); [111] ( c ) при разных температурах. Горизонтальная линия указывает положение химического потенциала в нижней полосе (пунктирная линия)

To calculate the sublattice magnetization and the spin-spin correlation function, we write down four additional linear differential equations for the Green's functions ((5aY br o/), USГ\ S? y J /for two sublattices y , y ' = 1 ,2, and two equations for the sublattice magnetization and the correlation function. The problem can be simplified if we consider the magnetic system in the adiabatic approximation and make some estimates of the temperature dependence of m, c. The free energy expansion procedure gives a power function m = m0 ^1 - T/TN . According to the elastic neutron scattering data [6], the sublattice magnetization is m0 = 0,94цB at T = 2 K . The spin-spin correlation function for the nearest neighboring sites can be estimated at the Néel temperature as

1 + r

s (1 + s). 3 (1 + r ) ’

( S ₀ ^a S “1) = 0,125.

At low temperatures, when the correlation radius of spin fluctuations ^ ~ a ( a is the lattice constant), the transverse spin-spin correlation function is calculated in the mean-field approximation ^ S a S _r^a=^ = 0,125 ( 1 - m ²) . The dependence c ( T ) in the paramagnetic phase is assumed to be symmetric with respect to the Néel temperature.

For tetragonal symmetry а (lattice constant in the plane)> c , the hopping parameters of current carriers should also be considered as anisotropic 0 1 / 0 ₀ = 0,92 .

Discussion of the results

The polaron excitation spectra for three directions are shown in Fig. 1 for the following parameters: I/t ₀ = 0,08, J/t ₀ = 2,06. Band splitting of free electrons is observed due to strong interaction with localized spins, which form an ordered state below the Néel temperature. The Fermi level is located in the lower zone near the chemical potential indicated with a dotted line in Fig. 1. Fermi energy and s – d interaction energies have comparable values. S-electrons form a spin density wave (SDW) with a wave vector located near the Fermi surface, since the Fermi energy is more than an order of magnitude higher than the magnetic excitation energy. SDW modulates the density of localized spins, which causes the appearance of additional satellites in the neutron diffraction pattern.

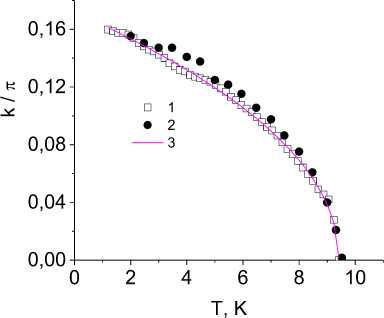
Fig. 2. Temperature dependence of the Fermi impulse ( 2 ) and the position of the satellite in the neutron diffraction pattern ( 1 ). The curve is an approximating 0,48 function Q ( T )~ ( T - T )     ( 3 )

Рис. 2. Температурная зависимость импульса Ферми ( 2 ) и положения сателлита на нейтронограмме ( 1 ). Кривая представляет собой аппроксимирующую 0,48 функцию Q ( T )~ ( T - T )    ( 3 )

0    5    10   15   20   25

T, K

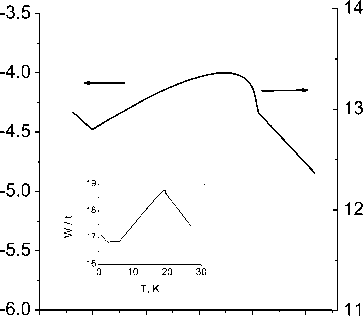
Fig. 3. Energy of the lower border of the band W _bot t and the upper border of the band W _top t as a function of temperature. The inset shows the temperature dependence of the bandwidth

Рис. 3. Энергия нижней границы полосы Wt и верхней границы полосы W _top t в зависимости от температуры. На вставке показана температурная зависимость ширины полосы

It was found that the evolution of the position of the satellite line with temperature occurs according to the power law [6]

Q ( T ) ^ ( T * - T ) ^V ,                                     (6)

with v = 0,48 , as it is shown in fig. 2. The calculated change in the Fermi momentum k F along [001] (Fig. 2) as a function of temperature is in good agreement with the experimental data. The calculated value k F = ( 0,0,0.14 ) at T = 1,8 K also agrees with the period of the spin modulation Q = ( 0,0,0.15 ) . The Fermi surface is a bounded region with the center of the band at T <  T * and vanishes at T = T* . The Fermi momentum lies in the range п/ 2 <  k_F < n with centers at the edges of the bands, where the spin-wave spectrum in CuB 2 O 4 is not observed. A decrease in the effective energy of interaction of selectrons with localized spins, caused by a decrease in the magnetization of the sublattice, leads to a shift of the bottom and top of the polaron band and an increase in the bandwidth, as it is shown in Fig. 3. In the paramagnetic phase, an increase in antiferromagnetic correlations upon cooling also leads to an increase in the passband.

To estimate the contribution of polaron excitations to the specific heat, the average value of the kinetic energy of the polaron K_p is modeled by the Green's function

K p =   &( k ) 1 1 dEf ( E ) Im G ^ ( E ) •                     (7)

The temperature dependence C = dKp/dT is shown in Fig. 4. The maxima of heat capacity are observed atT1,7; 4,5K. The temperatures corresponding to the maxima of the heat capacity are in good agreement with the experimental data [19]. Transport properties, such as conductivity, can be obtained from the Kubo formulas in the limit d ^ x [20]

П,       , f (а')- f (а'+®j d а' Iа (а', а'+ а) —-— -----------,

а                      а

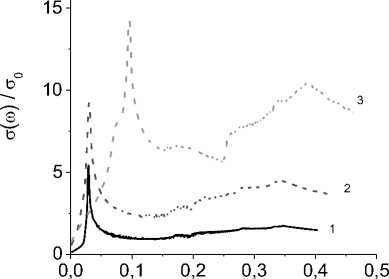
Iа(а1, а2 ) = A S Im Gа( k, а1) Im Са( k, а2 ), п к where а 0 is a constant that determines the dimension of conductivity. The temperature dependence of the conductivity а(а^ 0) is shown in Fig. 5. Below TN the value а decreases sharply with an increase in the sublattice magnetization. When T16 Kthe change in the sign of the derivative of the chemical potential from dp/dT < 0 to dp/dT > 0 correlates with the singularity in dа/dT. The drop in conductivity at T > 5 K arises due to the shift of the minimum of the band bottom from the center of the band (0, 0, 0) to (1, 0, 1), (0, 1, 1). It is shown in Fig. 1, b. Optical conductivity is presented in Fig. 6 and has two maxima. The first peak is the result of intraband transitions, and the broad maximum а(а) is attributed to transitions between the lower and upper zones. The temperature dependence а( T) can be observed in the infrared range with the amplitude of the electric field E0 and the plane polarized wave with the frequency а. The absorption power supplied to the system is defined as P (а) = 2 E02Re [а z (а)] [21].

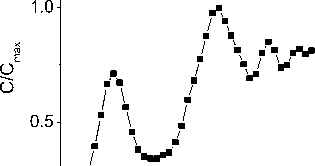
0.0

T, K

Fig. 4. Temperature dependence of the heat capacity normalized to the maximum value induced by spin polarons

Рис. 4. Температурная зависимость теплоемкости, нормированной на максимальное значение, индуцированное спиновыми поляронами

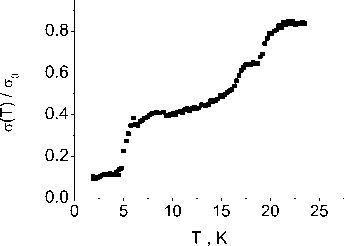
Fig. 5. Temperature dependence of conductivity а ( T ) at а^ 0

Рис. 5. Температурная зависимость проводимости а ( T ) при а > 0

и , eV

Fig. 6. Optical conductivity at temperatures T = 2 K ( 1 ), 7 K ( 2 ) and 17 K ( 3 )

Рис. 6. Оптическая проводимость при температурах T = 2 К ( 1 ), 7 К ( 2 ) и 17 К ( 3 )

The peculiarities of the low-temperature behavior of the heat capacity and conductivity arise due to the modification of the polaron excitation band. The maximum of the density of states is located near the Fermi level and shifts to the high-energy region at T >  10 K . An increase in the hole concentration leads to a decrease in the critical temperature for the formation of modulation of the spin structure T* . The maximum heat capacity also shifts to low temperatures.

Conclusion

Let's summarize the main results. Spin-polarized s-electrons form a spin density wave with a period equal to the Fermi momentum. The spin density wave modulates the localized spin density as a result of strong s – d coupling. The estimate of the temperature dependence of the Fermi momentum of the spin polaron is in good agreement with the evolution of the satellite position as a function of temperature in CuB 2 O 4 . The maximum low-temperature heat capacity arises as a result of the displacement of the minimum of the zone lower boundary from the center of the zone (0, 0, 0) to (1, 0, 1), (0, 1, 1). The calculations presented predict a sharp decrease in the conductivity and intensity of infrared absorption at the Néel temperature.