Increasing software reliability of a distributed control systems

The quality of any computer network (CN) can be assessed using its main characteristics. These include the completeness of the functions performed, performance, throughput, reliability, security, transparency, scalability and versatility [1]. None of these criteria can definitely be called the most important, but among them there are several of the most significant. One of such criteria is reliability [2–5].

Reliability is the ability of the computer network (CN) to reliably perform certain functions under given conditions for a given period of time with a sufficiently high probability [6-8]. With a low level of reliability of the CN, the functionality of systems responsible for indicators of other quality criteria will also be affected. Therefore, ensuring the reliability of the CN is a priority task when building a computer network [9].

It is impossible to eliminate the possibility of failures, and therefore ensuring reliability is to reduce the number of errors that a user may encounter during the operation of the network. One of the most proven and trusted ways to increase reliability is the introduction of redundancy [10; 11].

In the hardware of the CN, redundancy serves to deal with periodically failing processors and buses. Hardware redundancy is introduced by reserving processor elements and interface buses. The required number of duplicated hardware components varies and depends on the failure rate and recovery time. Calculating the optimal number of these components is the main difficulty of introducing hardware redundancy.

Software redundancy cannot be achieved by duplication as errors that occur in software modules have an internal nature [12], which leads to the appearance of the same errors in identical copies. Therefore, instead of copies, it is necessary to create new versions that differ from each other in the programming language, the programmers who developed them, and the algorithms used. Due to internal differences between different versions, the probability of similar failures is minimized [13; 14].

Software redundancy is not applied to the entire program or software package – it is used to increase the reliability of modules that are critical for the functioning of the entire network as a whole or to which users and other modules most often turn [15]. As in the case of hardware redundancy, the number of introduced versions of software modules must be selected for each individual network, which, combined with the labor costs of developing new versions, indicates a non-trivial task of effectively using software redundancy. To conduct research on this problem, a mathematical model to assess the reliability of the software is used.

Software reliability assessment model

The reliability of the network software is affected by its hierarchical levels – the dependence of software modules on each other can lead to a failure in one module spreading across the architecture of the entire network software [16]. The model describing the reliability of the network software should take into account the influence of the hierarchy of software modules on failures and downtime [17].

Designations used in the model:

• 1)    M – the number of architectural levels in the architecture of the network software;

• 2)    N j is the number of modules at the level j , j ∈ {1, ..., M };

• 3)    D ij is the set of module indexes that depend on module i at the level j , i ∈ {1, ..., N j }, j ∈ {1, ..., M };

• 4)    F ij is a failure event that occurred in module i at level j , i ∈ {1, ..., N j }, j ∈ {1, ..., M };

• 5)    PU ij is the probability of using module i at level j , i ∈ {1, ..., N j }, j ∈ {1, ..., M };

• 6)    PF ij is the probability of a failure in module i at level j , i ∈ {1, ..., N j }, j ∈ {1, ..., M };

• 7)    PL ^ij - conditional probability of a failure in module m at level n when a failure occurs in module i at level j , i ∈ {1, ..., N j }, j ∈ {1, ..., M }, n ∈ {1, ..., N m }, m ∈ {1, ..., M };

• 8)    TA ij is the relative access time to module i at level j , i ∈ {1, ..., N j }, j ∈ {1, ..., M }, defined as the ratio of the average access time to the module i at level j to the number of failed modules at small levels of the architecture at the same time;

• 9)    TC ij is the relative time of the failure analysis module i to level j , i ∈ {1, ..., N j }, j ∈ {1, ..., M }, which is defined as the average time of failure analysis in the module i at the level j , i ∈ {1, ..., N j }, j ∈ {1, ..., M }, to the number of failed modules at all levels of architecture, analyzed at the same time;

• 10)    TE ij is the relative time for Troubleshooting in the module i to level j , i ∈ {1, ..., N j }, j ∈ {1, ..., M }, defined as the ratio of the mean recovery time in the module i at the level j , i ∈ {1, ..., N j }, j ∈ {1, ..., M }, to the number of failed modules at all levels of the architecture, which is a fault at the same time;

• 11)    TU ij – relative time of the module being used i at the level j , i ∈ {1, ..., N j }, j ∈ {1, ..., M }, which is defined as the average usage time of module i at the level j , i ∈ {1, ..., N j }, j ∈ {1, ..., M }, to the number of modules at all levels of the architecture used at the same time;

• 12)    Z ij – the set of versions of module i , at the level j , k = 1, ..., K ;

• 13)    T ij – the labor intensity of developing module i at level j ;

• 14)    T ^k – the labor intensity of developing version k of module i at level j , k ∈ Z ij in person-hours;

• 15)    NVX ij – the labor intensity of developing an acceptance test (for RB ) or a voting algorithm (for NVP );

• 16)    T s – total network labor intensity;

• 17)    B ij is a dichotomous variable that takes the value 1 (then NVP ij = 0, RB ij = 0), if in the software module software redundancy is not used , otherwise it is equal to 0;

• 18)    NVP ij is a dichotomous variable that takes the value 1 (then B ij = 0, RB i = 0) if the software module uses N -version programming software redundancy, otherwise it is equal to 0;

• 19)    RB ij is a dichotomous variable that takes the value 1 (then B ij = 0, NVP ij = 0) if the software module uses software redundancy according to the recovery block method, otherwise it is equal to 0;

• 20)    TR is the average downtime of the CN software, defined as the time during which the system cannot perform its functions;

• 21)    MTTF is the average time of occurrence of a failure in the network software of the CN, defined as the time during which there are no failures in the system;

• 22)    S is the readiness coefficient of the CN software;

• 23)    T s is the total labor intensity of the implementation of the network software.

The average failure time of the network software of the computer network is equal to:

M Nj

MTTF=SS{ PUj «(1 - PFj )x [ TU + j=1 i =1

(                        Лк x TUnm + S ((1 - PL™ )x TUim )

к          l ^ D nm                       ) )

M   Nm ,

+ S S (1 - PLjm )

+

( m = 1 ) & ( m * j ) n = 1 к

+

(

S ^{( 1 -} PL ,

k £ D ij

к

(

x TU. +

к

M   Nm

У  Ш1 - PLkLV( тип + nm       nm

( m = 1 ) & ( m * j ) n = 1

+ S ( ( 1 - ^pL m ) x TU m ) ))))]}.

l ^e D nm

The average downtime of the network software of the computer network is equal to:

M^M j

TR = SS{PUij xPFij x[(TAj + TCij + TE,) + j=1 i=1

M   Nm

+ S S P j x

( m = 1 ) & ( m * j ) n = 1 к

кк

(TAnm + TCnm + TEnm ) + S (P^ x (TAlm + TClm + TElm ))

x

l eDnm) )

x S [ PL x[(TA. + TCtl+ k e Dij

M   N m

+ S S PL - ( m = 1 ) & ( m * j ) n = 1 к

кк

(TAnm + TCnm + TEnm) + S (PLm x (TAm + TClm + TEm )) l£Dnm) )

Both of these formulas take into account the hierarchy of modules and therefore are universal for any network software with architectural levels. According to them, the readiness coefficient of the software part of the CN is also determined:

MTTF

= MTTF + TR

.

By themselves, these indicators consider the reliability of the network software of the computer network only in its initial state. Two main methods of introducing multiversion are described in [18]: NVP ( N- version programming) and RB (recovery block).

NVP implies that all versions of the program are executed in parallel, and the result of their work is determined using the voting algorithm [19]. The reliability of the multiversion module i at the level j , built from K versions by the method of multiversion programming for any k , is equal to

R j = p v ¹ - n ( 1 - p k ) ,

k = 1

where p ^v is the probability of failure-free operation of the voting algorithm; p ^k - the probability of failure-free operation of version k e Z ij .

With the RB approach, multiversion is introduced through the addition of several versions of the computing module, the creation of an acceptance test that verifies the operation of the versions, and a subprogramme that, based on the test results, either accepts the result of the module, or selects another version and restarts the calculation [19]. Reliability of such a module:

Kk

Rij =S pikpAT П((1 - 4) pi+pj (i - pAT)), ke ZijI where pAT is the probability of failure-free operation of the acceptance test for module i, i = 1, ..., N at level j, j = 1, ..., M; pk is the probability of failure of version ke Zij.

For any of the approaches, the probability of failure will be calculated as

PE. = \-R... ijij

When introducing software redundancy, the question always arises: exactly how many versions is needed to introduce? The possibility of using multiversion is limited by many factors. One of the most significant of them is the labor intensity, reflecting the labor costs on building a network, directly dependent on the number of versions of software modules that need to be developed. To reflect this limitation, the model has the formula [20]:

MN i

T s = YL j = 1 i = 1

BT + ( NVP

+ RB ij V

K

NVX„ ■ YT ij                 ij k eZij   )

In the study of CN, this indicator can be used to find the optimal number of versions for each software module. There are different ways to explore the network, but they all have the same points: the labor intensity of T s should strive for a minimum, and the readiness factor S should strive for a maximum.

Investigation of the reliability of the network software

Based on the considered model, a software system has been developed that allows calculating the reliability of the network software and conducting research on the specified input data.

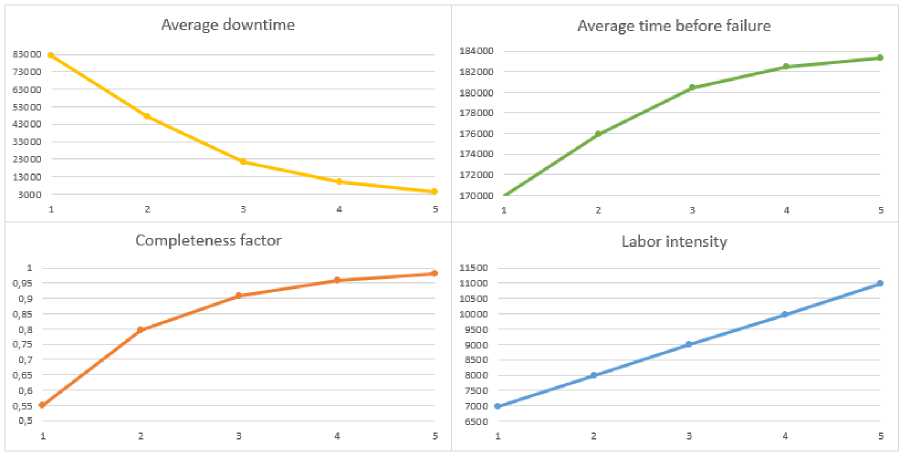
To conduct the study, consider the network software consisting of 10 modules. Assume that all modules, with the exception of one, work without failures (i.e. have reliability equal to 1). The overall reliability of the software will be determined by the reliability of the critical module with a value of 0.55. Software redundancy is introduced into it by the NVP method, the complexity of developing new versions of this module is taken for 1000.

The table shows the results of the dependence of the reliability indicators of the network software on the versions of one of its modules, and the figure clearly shows the dynamics of parameter changes.

Results of the network software study

Number of critical module versions	Average downtime	Average time before the failure	Readiness ratio	Labor intensity
1	82115	169838	0.5500	6981
2	47509	175844	0.7975	7981
3	21373	180379	0.9089	8981
4	9619	182420	0.9590	9981
5	4340	183336	0.9815	10981

Computer network software parameters’ change dynamics Динамика изменения параметров ПО ВС

Conclusion

The obtained graphs allow us to determine the number of new versions of the dedicated module, at which the increase in the cost of developing a new software element begins to exceed the increase in software reliability. At some point, the introduction of new versions ceases to be expedient, since the costs begin to exceed the returns received.

In the situation chosen for the example, the reliability of the entire network software depends on one of its modules. When designing real network software, there will be significantly more such modules, which will greatly complicate the task of research. This underlines the importance of the labor intensity parameter, which is determined by the model along with the reliability of the network software. Comparing the increase in labor costs with the increase in the software reliability of the network, you can see at what point you should stop adding new versions of software modules.

Thus, an approach was considered that allows both evaluating and improving such parameters of the network software as reliability and labor costs. To do this, on the basis of a mathematical model for assessing reliability and labor costs for development, the software was created to study the dependence of the reliability of the software and labor costs for its development on the number of versions for problematic, from the point of view of reliability, software modules. The dynamics of changes in the parameters of reliability of network software and labor costs for its development from the number of versions of one of its software modules is analyzed. From the results obtained, it can be concluded that it is important to take into account the complexity parameter when studying the reliability of a network into which software redundancy is introduced.