Индекс сингулярности и орбитальный угловой момент пучка с гибридной поляризационной сингулярностью

Хорошо известно, что вихревые лазерные пучки (например, Лагерра–Гаусса, Бесселя–Гаусса) имеют винтовой волновой фронт с фазовой сингулярностью (неопределенностью) на оптической оси, имеют топологический заряд (ТЗ) [1] и орбитальный угловой момент (ОУМ) [2]. Векторные пучки с неоднородной поляризацией (например, радиальной, азимутальной) также могут иметь поляризационные сингулярности, которые характеризуются индексами поляризационной сингулярности [3, 4]. Возникает вопрос: могут ли поляризационные вихри (например, цилиндрические векторные пучки [5]) иметь некоторый поляризационный ОУМ (пОУМ)? И какой физический смысл у пОУМ? Обычный орбитальный угловой момент скалярного вихревого поля показывает азимутальную скорость изменения фазы и проявляется в том, что световой пучок с ОУМ может вращать частицу по круговой траектории [6]. Аналогично можно найти величину пОУМ, которая показывает величину азимутальной скорости изменения наклона вектора линейной поляризации в сечении пучка. На практике такой поляризационный вихрь будет осуществлять массоперенос [7] в среде, чувствительной к поляризации [8], и формировать спиральный рельеф поверхности [9]. Например, в работе [9] спиральный массо-перенос в тонкой пленке изополимера (халькогенидное стекло) осуществлен с помощью векторного лазерного пучка, у которого направление вектора линейной поляризации линейно менялось с изменением азимутального угла. То есть пучок света с азимутальным изменением вектора линейной поляризации «заставляет» молекулы изополимера смещаться по окружности. Можно сказать, что такой поляризационный вихрь обладает поляризационным ОУМ. Векторные поля с точками поляризационной сингулярности (c V- и С-точками и линиями) описываются с помощью индексов поляризации [3], аналогичных топологическому заряду (ТЗ) скалярных полей. Логично также рассмотреть для векторных полей и другую характеристику, аналогичную ОУМ для скалярных полей. Заметим, что у ТЗ и ОУМ много общего, но есть и различия. ОУМ определяется амплитудой и фазой скалярного поля, а ТЗ – только фазой.

Известно также, что световые поля с эллиптической и круговой поляризацией обладают спином [10] и спиновым угловым моментом [11], с помощью которого они могут вращать поглощающие частицы вокруг центра масс [12]. Сила рассеяния, с которой действует свет на частицу, может зависеть от ротора вектора спинового углового момента [13, 14]. Трехмерное распределение поляризации лазерного пучка используется для ускорения заряженных частиц [15– 17]. Цилиндрические векторные пучки с неоднородной линейной поляризацией, у которых нет спина, также используются для манипуляции частицами [18–20]. С неоднородной поляризацией света связаны такие оптические эффекты, как спиновый и орбитальный эффект Холла [21, 22], поляризационные ленты Мебиуса [23], оптические колеса [24, 25], спин-орбитальная конверсия [26, 27]. Например, спин-орбитальная конверсия в остром фокусе приводит к тому, что исходный гауссов пучок с круговой поляризацией в фокусе формирует азимутальный поток энергии, который может вращать частицы по окружности [28]. Из-за орбитального эффекта Холла в остром фокусе векторного светового поля с неоднородной линейной поляризацией локально формируются замкнутые потоки энергии, которые также могут вращать частицы по окружности [29]. Наличие обратного потока энергии в фокусе векторных полей связано с ротором спинового углового момента [30].

Поэтому, на наш взгляд, интересным является рассмотрение ОУМ для световых полей с неоднородной поляризацией. В данной работе будут рассмотрены два новых ОУМ: поляризационный ОУМ, который пропорционален азимутальной скорости изменения наклона вектора поляризации, и гибридный ОУМ, который пропорционален азимутальной скорости изменения степени эллиптичности поляризации. Приведено сравнение указанных ОУМ с обычным ОУМ, применяемым для скалярных и векторных вихревых пучков.

• 1.    Топологический заряд скалярного вихревого поля и индекс поляризационной сингулярности векторного поля

Будем рассматривать параксиальные векторные когерентные световые поля (пучки), у которых в сечении имеют место поляризационные сингулярности. Хорошо известны векторные пучки с неоднородной линейной поляризацией, у которых могут быть точки неопределенности направления вектора линейной поляризации. Такие точки называются V-точками. Если имеется векторный пучок с неоднородной эллиптической поляризацией, то точка с круговой поляризацией будет точкой поляризационной сингулярности (C-точкой), так как в этой точке не определено направление большой оси эллипса поляризации. Такие точки поляризационной сингулярности хорошо изучены [3, 4]. Для их ха- рактеристики используются индексы поляризации: индекс Пуанкаре–Хопфа [31] и индекс Стокса [32]. При формальном описании этих индексов будем следовать работе [33], в которой индексы поляризационной сингулярности определены аналогично ТЗ скалярных вихревых пучков. Итак, ТЗ скалярных оптических вихрей будем определять согласно формуле М. Берри [1]:

• 1        2- д

TC = 2 П М a^arg E ( r , " ' d ^ф ,           ⁽¹⁾

где E ( r, φ) – комплексная амплитуда скалярного светового поля, зависящая от поперечных полярных координат, продольная ось z направлена вдоль оптической оси пучка, arg – аргумент комплексного числа (фаза светового поля), lim – предел по радиальной координате r , стремящейся к бесконечности. Выражение (1) подсчитывает все нули комплексной аналитической функции, находящиеся внутри окружности бесконечного радиуса. Теоретически некоторые нули функции могут находиться на бесконечности, тогда они должны учитываться с множителем 1/2. Но на практике при численном расчете ТЗ окружность всегда имеет конечный радиус, поэтому часть «далеких» нулей может быть пропущена.

Если у скалярного светового поля комплексная амплитуда имеет вид:

E ( r , ф ) = A ( r ) exp( in ф ),                            (2)

то, подставляя (2) в (1), получим, что TC = n .

Векторные поля в начальной плоскости описываются только поперечными проекциями вектора напряженности электрического поля (вектором Джонса):

( E_x ( r , ф ) ^

E ( r , Ф ) = L       I .                             (3)

L E y ( r , ф ) )

Если функции E x и E y действительные, то в сечении векторного пучка имеется неоднородная линейная поляризация, которая может менять направление вектора поляризации в каждой точке сечения пучка. Тогда можно формально записать скалярную комплексную амплитуду вида

E c ( r , ф ) = E x ( r , ф ) + iE y ( r , ф ), (4)

к которой можно применить формулу (1). В этом случае индекс поляризационной сингулярности Пуанка-ре–Хопфа [31] для векторного пучка (3) будет равен выражению:

П = T-^mf —arg E c ( r , ф ) ! d ф •              (5)

2n ^r ^” J дф ^{L           J}

Индекс (5) показывает, какое целое число оборотов на угол 2π сделает вектор линейной поляризации в сечении пучка (3) при обходе по окружности большого радиуса с центром на оптической оси. Размер радиуса окружности на практике должен быть таким, чтобы внутри окружности оказались все точки с поляризационной сингулярностью.

Если функции E x и E y в (3) комплексные, то использовать индекс (5) нельзя, так комплексная амплитуда (4) не будет иметь требуемой структуры. В этом случае применяется индекс Стокса [32]. Для поля (3) можно получить действительные компоненты вектора Стокса:

S 1 = Ex Г-I Ey f,

S 2 = 2Re ( E x E y ) ,                                (6)

S 3 = 2Im ( E * E y ) .

Из первых двух действительных компонент вектора Стокса можно получить скалярную комплексную амплитуду Стокса:

S c = S i + iS 2 .                                          (7)

Используя формулу Берри (1) и комплексное поле Стокса (7), можно определить индекс поляризационной сингулярности Стокса для векторного поля (3) в виде:

c = — lim f —Targ Sc (r, ф)! dФ •(8)

2nr>' 0 дф LJ

Можно показать, что индекс Стокса в 2 раза больше индекса Пуанкаре–Хопфа.

2. Орбитальный угловой момент скалярного и векторного полей

Вернемся к скалярным вихревым пучкам, которые характеризуются не только ТЗ (1), но и ОУМ [2]:

® 2п

J z = Im J J E * ( r , 00

“ 2 п             д

J v,z = Im J J E x ( r , ф) —

0 0 L         ^дф

д

⁺ E y ^{( r} , ^ф) _дф E y ^{( r}

E _x ( r , ф ) +

rdrd ф .

Физический смысл векторного ОУМ (11) в усреднении азимутальной скорости изменения фазы каждой их поперечных компонент поля. Например, для начального векторного вихревого поля вида:

„ . . A ( r ) f exp⁽ in ф ) E i ^{( r} , ф ) = -/rl

V 2 V exp( im ф )

ОУМ (11) примет вид:

/ ।    \                 ® 2п

J vz = lI W , W = 2 n J J A ² ( r ) rdr .

v ² /                 0 0

В (13) W – это мощность пучка. Из (13) видно, что ОУМ пропорционален среднему арифметическому топологических зарядов вихрей в каждой проекции векторного поля (12). ОУМ (11) векторного поля с любой неоднородной линейной поляризацией, когда функции E x и E y в (3) действительные, равен нулю. То есть, если мы индексами (5) и (8) можем характеризовать поляризационную сингулярность, ОУМ (11) не позволяет характеризовать поляризационные особенности векторного поля, а позволяет характеризовать только фазовые особенности у поперечных проекций электрического поля. Мы должны искать аналоги ОУМ (11), которые позволят характеризовать поляризационные вихри. Рассмотрено несколько кандидатов на ОУМ для поляризационных вихрей. Запишем векторное поле (3) через реальные и мнимые части проекций E x и E y :

д

ф ) — E ( r , ф ) rdrd ф .

Из сравнения (1) и (9) видно, что ТЗ и ОУМ – разные характеристики вихревых пучков, так как в (1) присутствует только фаза светового поля, а в (9) – и фаза, и амплитуда. Для векторных световых полей, аналогично (9), можно определить вектор ОУМ в виде [34]:

J = Im J J E E p ( r ^xV ) E p ^rd^rd Ф ,            (¹⁰)

0 0 p=x, y, z где r = (x, y, z) – радиус-вектор в точку сечения пучка. Но для параксиальных векторных полей, для которых можно пренебречь продольной проекцией вектора напряженности электрического поля, существенна только продольная компонента вектора (10). Выпишем поэтому продольную компоненту вектора ОУМ (10) для векторного поля (3):

X f E x ( r , ф ) ^ f A x + iB x ^ E ( r , ф ) = l I = l I .

E y ( r , ф )J ^ A y + iB y)

В обозначениях (14) ОАМ (11) примет вид:

“ 2 п      д

J v , z = JJ A x— B x - B x 0 0 L ^дф

д

— Ax + дф ^x

. 3 _ _ д .

+ A y — B y - B y — Ay rdrd ф . дф дф J

Из (15) видно, что обычный ОУМ, примененный к векторному полю с неоднородной линейной поляризацией, когда функции E x и E y в (14) действительные, будет равен нулю.

3. Орбитальный угловой момент неоднородного векторного поля с локальной линейной поляризацией

Поэтому введем в рассмотрение другое определение ОУМ, отличное от (9) и (15), которое бы характеризовало векторные пучки с неоднородной поляриза-

цией. Назовем его поляризационный ОУМ (пОУМ) и определим в виде:

да 2 п                 д

J p , z = Re J J E x ( r , ф)— E y ( r , ф )

0 0 L          дф

д- Ey( r, ф)—Ex (r, ф) rdrd Ф =

^ 2п /^     ^

= [f| A x — Ay - A y — Ax +

J J l дф дфд д ^

+ By — By - By — By \ rdrd ф .

xyyx

дф дф J

Из (16) видно, что мнимые и действительные части под интегралом в (16) разделены, и поэтому ОУМ (16) будет отличен от нуля, когда функции E x и E y в (14) действительные. Проверим это на примере. Рассмотрим в качестве начального поля цилиндрический векторный пучок с вектором Джонса в виде:

( cos( n ф)^

E 2 ( r ,Ф) = A ( r )1;Л . (17) l Sin( n Ф ) J

Подставим (17) в (16), получим, что J p,z = nW , а применение уравнения ОУМ (15) к полю (17) дает ноль: J v,,z = 0. Заметим, что у цилиндрического векторного пучка (17) индекс поляризационной сингулярности (5) равен n , а индекс Стокса (8) равен 2 n . Индекс (5) для поля (17) показывает, что при обходе в сечении пучка по замкнутому контуру вокруг оптической оси векторы линейной поляризации сделают n полных оборотов. Таким образом, пОУМ (16) показывает среднюю азимутальную скорость поворота векторов линейной поляризации в сечении неоднородного векторного пучка. Заметим также, что поляризационный ОУМ (16), примененный к вихревому пучку с круговой поляризацией

E, = A (r )!exp(inф) f1 \ (18) 42 l-iJ даст такой же результат, Jp,z = nW. То есть поляризационный ОУМ показывает среднюю азимутальную скорость изменения и фазы вихревого поля с круговой поляризацией (18) и азимутальную скорость поворота векторов линейной поляризации пучка с неоднородной поляризацией (17). Хотя для оптического вихря с линейной поляризацией пОУМ будет равен нулю.

4. Орбитальный угловой момент гибридного векторного поля с эллиптической поляризацией

Можно модернизировать определение пОУМ (16), взяв вместо реальной части комплексного числа мнимую часть и вместо разности сумму слагаемых, тогда получим новое определение поляризационного ОУМ. Чтобы отличать его от (16), назовем такой ОУМ гибридным поляризационным ОУМ (гОУМ):

“ 2п             Д

Jh.z = Im J J Ex( r, ф) — Ey (r, ф) +0 0 L          дф

д

+ E y ( r , ф ) — E x ( r , ф ) rdrd Ф =

^ 2 п

= C | Ax — By + Ay — By оJ l дф дф

-

-

By — A

дф

-

By — Ay yx

дф

rdrd ф .

Если подставить поле (17) в гОУМ (19), то получим ноль, так как в (19) в каждом слагаемом присутствует мнимая часть числа, а поле (17) действительное и не имеет мнимой части. Рассмотрим гибридное векторное поле, которое проявляет свойства и цилиндрического векторного поля (17), и поля с круговой поляризацией:

(cos( n ф )

E ₄( r , ф) = A ( r ^..^J .                  (20)

1 1 Sin( n Ф ) J

Векторное поле (20) с увеличением азимутального угла меняет поляризацию от линейной до эллиптической и круговой и далее опять меняется от эллиптической до линейной, периодически повторяясь. Подставив (20) в (19), получим J h,z = nW . То есть гибридный ОУМ (19) показывает азимутальную скорость изменения степени эллиптичности у пучков с неоднородной эллиптической поляризацией. Если сравнить обычный ОУМ для векторного поля и гибридный ОУМ (19), то можно увидеть, что ОУМ (19) будет отличным от нуля, если у пучка (14) проекции поля чисто мнимые или чисто действительные, как у пучка (20). А чтобы обычный ОУМ (15) был отличным от нуля, нужно, чтобы у начального поля у обеих проекций поля были и мнимые, и действительные части. Рассмотрим в качестве примера вихревой пучок с топологическим зарядом m и цилиндрической поляризацией порядка n :

,    у f cos( n ф )

E ₅( r , Ф ) = A ( r )exp ( im ф ) |          I .              (21)

l Sin( n Ф ) J

Подставим (21) в (15), получим, что обычный ОУМ пучка (21) равен J v,z = mW , а если (21) подставить в (16), то получим, что поляризационный ОУМ пучка (21) равен J p,z = nW . Гибридный ОУМ у пучка (21) равен нулю. Аналогично рассмотрим вихревой пучок с гибридной поляризацией вида:

E 6 ( r , ф ) = A ( r ) exp ( im ф )

cos( n ф ) i sin( n ф )

.

Для пучка (22) нетрудно показать, что будут выполняться равенства: J v,z = mW , J p,z = 0, J h,z = nW.

5. Вихревой и поляризационный орбитальные угловые моменты пучка Пуанкаре

Рассмотрим вектор Джонса пучка Пуанкаре:

подобраны так, что обычный векторный ОУМ в три раза меньше поляризационного ОУМ, плотность которого повёрнута на три разных угла.

E ? ( r , ф ) = A ( r )

ae ^n Ф+ i ^a

- i

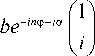
a ² + b ² = 1/2.

Постоянные a, b и α задают точку (состояние поляризации) на поляризационной сфере Пуанкаре. Поэтому обычный вихревой ОУМ (15) будет зависеть от параметра a :

J v , z = 2 n ( a ² - b²)W = n (4 a ² - 1) W . (24)

Из (24) видно, что максимальное значение ОУМ достигает при a = 1/42 и равен J pz = nW, а пучок Пуанкаре при этом является оптическим вихрем с топологическим зарядом n и левой круговой поляризацией. Если a =0, то ОУМ достигает своего минимального отрицательного значения, J v,z = – nW, а пучок Пуанкаре при этом является оптическим вихрем с топологическим зарядом – n и правой круговой поляризацией. При условии, что a = b = 1/2, пучок Пуанкаре (23) становится максимально запутанным и теряет свой вихревой ОУМ, становясь цилиндрическим векторным пучком n -го порядка (17): J v,z = 0. Заметим также, что ОУМ не зависит от постоянной фазы α. Во всех других случаях, 0< a <  1/2 и 1/2< a < 1/ 2 , модуль обычного ОУМ меньше n : 0 < | J v , z / W | <  n .

По-другому ведет себя поляризационный ОУМ (16) пучка Пуанкаре (23) в зависимости от параметров a, b и α . Он от них не зависит и равен:

J p , _z = 2 n ( a ² + b ²)W = nW ,

J _p , z (r , ф ) = 2 n (a ² + b ²) A ²( r ) + (25) + 4 abn cos ( 2 n ф + a ) A ² ( r ).

Можно сказать, что поляризационный ОУМ пучка Пуанкаре является его инвариантом. Второе уравнение в (25) показывает, что распределение плотности пОУМ зависит от азимутального угла φ, если a и b отличны от нуля, и меняет знак за один полный оборот вокруг оптической оси 4 n раз. Полный пОУМ поля (23) равен J p,z = nW. А гибридный поляризационный ОУМ (19) пучка Пуанкаре (23) равен нулю: J h,z = 0 .

6. Моделирование

Пучки Пуанкаре (23) при a ² = 1/2, b ² =0 или, наоборот, a ² =0, b ² = 1/2 сводятся к оптическим вихрям с круговой поляризацией. При a ² = b ² = 1/4 они сводятся к безвихревым пучкам с цилиндрической поляризацией. Поэтому для моделирования таких пучков представляют интерес другие значения a и b . На рис. 1 показаны распределения интенсивности и поляризации трёх пучков, в которых значения a и b

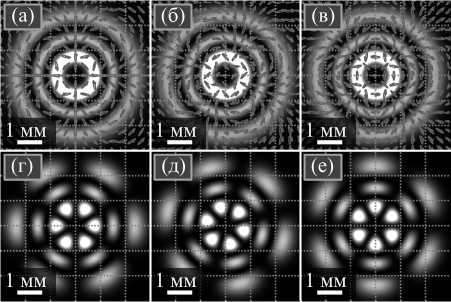
Рис. 1. Распределения интенсивности и поляризации (a – в), а также плотности поляризационного ОУМ (г – е) трёх пучков Пуанкаре с разным значением угла α. Для расчётов использовались следующие значения параметров: радиус перетяжки 1 мм, нижний (радиальный) и верхний (азимутальный) индексы пучка Лагерра–Гаусса p = 2 и m = 3, весовые коэффициенты пучка Пуанкаре a2 = 1/3 и b2 = 1/6. Фазовая задержка между положительным и отрицательным вихрем равна α = 0 (a), – 3π/2 (б), – π (в)

Из рис. 1 видно, что во всех трёх случаях формируется левая эллиптическая поляризация, поскольку весовой коэффициент такого пучка в суперпозиции (23) превышает коэффициент пучка с правой эллиптической поляризацией.

Фазовая задержка между положительным и отрицательным вихрем пучка Пуанкаре подобрана так, что, согласно теории, максимум плотности поляризационного ОУМ должен быть при полярном угле φ =0, φ = π/4, φ = π/2. На рис. 1 видно, что плотности поляризационного ОУМ действительно повёрнуты на эти углы.

Согласно (24), векторный ОУМ такого пучка, нормированный на его мощность, равен n /3 = 1, в то время как нормированный поляризационный ОУМ (25) равен n =3. При расчёте были получены значения J v , z / W = 0,999 и J p , z / W = 2,997 (для всех трёх значений угла α).

7. Эксперимент

В этом эксперименте, схема которого показана на рис. 2, цилиндрический векторный пучок (17) при n =2 был получен с помощью векторной волновой пластинки VWP (Thorlabs WPV10-633) и гауссова лазерного пучка с длиной волны 633 нм. Векторная волновая пластинка преобразует падающий на нее линейно поляризованный свет в векторный пучок, направление поляризации которого приведено на рис. 3 а . На рис. 3 б – д показан снимок получившегося на поляризационную камеру A7500PG400E (разрешение – 2448×2048, размер пикселя – 3,45 мкм) пучка. В данной камере перед каждым пикселем регистрирующего сенсора расположен поляризатор, ориенти-

рованный горизонтально (рис. 3 б ), либо вертикально (рис. 3 в ), либо повернутый под углом 45 (рис. 3 г ) или 135 градусов (рис. 3 д ). Далее цилиндрический векторный пучок последовательно проходил через четвертьволновую пластинку и поляризатор P 2 , ориентированный под углом 45 градусов к четвертьволновой пластинке. После такого последовательного прохождения волновой пластинки и поляризатора векторный пучок преобразовывался в оптический вихрь. Изображение получившегося вихря приведено на рис. 4 а . Для определения топологического заряда вихря получившийся пучок проходил через цилиндрическую линзу CL, распределение интенсивности в фокусе линзы приведено на рис. 4 б . Из рис. 4 б видно, что в фокусе формируется пятно с тремя максимумами и двумя минимумами. Следовательно [35], ТЗ вихря на рис. 4 а равен двум, а значит, и пОУМ пучка тоже равен двум: J p,z /W = n .

Laser

PH

L 1

D

P 1 VWP    λ /4 P 2    CL ^CMOS

Рис. 2. Схема эксперимента: Laser – лазер с длиной волны 633 нм, M 1 , M 2 – зеркала, PH, D – пинхол и диафрагма для фильтрации шума в пучке, L 1 – сферическая линза, P 1 – поляризатор,VWP – q-пластинка (q = 2), λ/4 – четвертьволновая пластинка, P 2 – поляризатор под углом

45 градусов, CL – цилиндрическая линза, CMOS – ПЗС-камера

Рис. 3. Направление поляризации в векторном пучке второго порядка (а) и его снимок на поляризационную камеру (б – д), регистрирующие отдельные состояния линейной поляризации в пучке: горизонтальную (б), вертикальную (в), под углом 45 (г) и 135 (д) градусов

а)

б)

Рис. 4. Изображение фазового вихря (а), распределение интенсивности в фокусе цилиндрической линзы (б)

Заключение

В данной работе по аналогии с известным векторным ОУМ, характеризующим азимутальное изменение фазы поперечных проекций электрического вектора, рассмотрены поляризационный ОУМ, характеризующий азимутальное изменение направления мгновенного вектора линейной поляризации, и гибридный ОУМ, который показывает азимутальное изменение степени эллиптичности эллипса поляризации в сечении гибридного векторного поля. Получены значения этих ОУМ для разных примеров векторных полей. Например, обычный и поляризационный ОУМ равны для оптического вихря с круговой поляризацией. А обычный и гибридный ОУМ отличны от нуля для оптического вихря с гибридной поляризацией. Векторный и гибридный ОУМ являются внешними ОУМ и не присущи отдельным фотонам в пучке, а присущи всему пучку и характеризуют массоперенос молекул вещества, чувствительного к поляризации. Предложены два способа экспериментального определения поляризационного ОУМ векторного пучка. Результаты эксперимента согласуются с теорией.

Работа выполнена при поддержке гранта Российского научного фонда № 23-12-00236 (в части теории)

и в рамках Государственного задания НИЦ «Курчатовский институт» (в части моделирования).