Индексные алгоритмы вычисления простых чисел с использованием метода кольцевой факторизации

кольца, отсеченная сектором, нумеруется так, как показано на рис. 1 [2].

Отметим сектора, которые начинаются: с единицы; с простых чисел, не участвовавших в получении примориала; а также со всевозможных, но меньших примориала, произведений этих простых чисел. Согласно методу кольцевой факторизации, в этих секторах лежат простые и составные числа, а в остальных (выделенных серым цветом на рис. 1) – только составные.

Для 7# = 210 начала секторов будут следующими: 1, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 121 = 11 × 11, 127, 131, 137, 139, 143 = 11 × 13, 149, 151, 157, 163, 167, 169 = 13 × 13, 173, 179, 181, 187 = 11 × 17, 191, 193, 197, 199, 209 = 11 × 19.

Метод кольцевой факторизации позволяет отсеять значительную часть составных чисел [1], а именно: для 3# отсеивается 66,66…% всех составных чисел, для 7# – больше 77%, а для 251# – около 90%.

На следующем этапе для исключения оставшихся составных чисел применяют различные

ВЕСТНИК 2013 № 4

ВЕСТНИК 2013 № 4

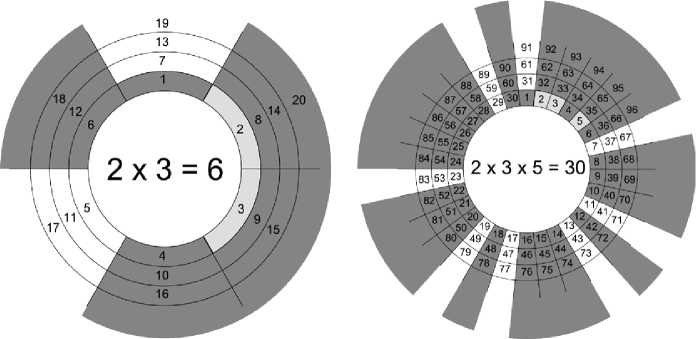
Рис. 1. Графическое изображение кольцевой факторизации для 3# и 5#

алгоритмы. В частности – решето Эратосфена, решето Аткина и другие. Появились и современные алгоритмы [3; 4].

Так, в работе [3] для нахождения полного множества простых чисел на определенном отрезке натурального ряда применяется аддитивное представление составных чисел вида {6 k ± 1}, где k = 1, 2, 3, … через простые числа того же вида.

Индексные алгоритмы с использованием кольцевой факторизации

Развитие положений работы [3] связано с реализацией индексного принципа нахождения составных чисел, заключающегося в вычислении не самих чисел, а массива соответствующих им индексов. Такой подход способен увеличить производительность алгоритмов вычисления простых чисел. В работе [4] реализован и исследован индексный алгоритм , построенный с использованием кольцевой факторизации для 3# = 6.

Целью настоящей работы является обоснование, разработка и исследование индексных алгоритмов, построенных с применением кольцевой факторизации для примориалов, превышающих значение 6.

Для удобства изложения введем такое понятие, как порядок индексного алгоритма, под которым подразумевается количество первых простых чисел, использованных при соответствующей кольцевой факторизации. Например, для 3# = 2 × 3 = 6 порядок индексного алгоритма равен 2, а для 5# = 2 × 3 × 5 = 30 порядок равен 3.

По аналогии можно также определить индексные алгоритмы первого и нулевого порядков. А именно, индексный алгоритм первого порядка есть отсев составных чисел из множества вида {2k + 1}, а нулевого – из чисел вида {1 k + 1}, где k = 0, 1, 2, … . Очевидно, что эти индексные алгоритмы являются решетами Эратосфена для нечетных натуральных чисел в первом случае и для всех натуральных чисел – во втором.

Сформируем индексный алгоритм второго порядка для нахождения простых чисел в заданном отрезке [ N _min; N _max], исходя из результатов работы [4]. Для этого применим кольцевую факторизацию для 3# к отрезку [1; N _max], введем обозначения q 6k = 6 k + 1, q 6 + 5 = 6 к + 5, где к = 0, 1, 2, … k (для максимально возможного k = k должно быть выполнено условие q + _k <  N max )S занесем эти данные в таблицу 1:

Таблица 1

Результаты кольцевой факторизации для 3# в табличном виде

Индекс	q 6 + k	q 6 + k
0	1	5
1	7	11
2	13	17
3	19	23
4	25	29
k max	6 k max + 1	6 k max + 5

В левом столбце таблицы приведена последовательность индексов 0, 1, 2, … k _max, в двух других столбцах – отображения этой последовательности в множества вида {6 k + 1} и {6 k + 5}, содержащие как простые, так и составные числа, а также единицу.

Перейдем к следующему этапу – отсеву оставшихся после кольцевой факторизации составных чисел из множеств {q +k} и {q6+5}, где k = 0, 1, 2, … kmax. Как показано в [4], все составные числа, кратные числам q + или q6+5, где i = 0, 1, 2, … imax (для максимально возможного i = imax должно быть выполнено условие (q+1 )2 < ≤ Nmax) можно исключить из таблицы 1, вычислив массив их индексов с помощью следующих соотношений.

Для фиксированного q6+i последовательность (m• q+1 + i), где m = 1, 2, 3, ... , индексирует все кратные ему составные числа во множестве {q6k}, а последовательность (m• q6+1 - i - 1), где m = 1, 2, 3, ... , индексирует все кратные q6+1 составные числа во множестве {q+5}. Для заданного отрезка [Nmin; Nmax] из вышеупомянутых последовательностей нужно выбирать те их члены, которые индексируют числа, содержащиеся внутри этого отрезка. Пример для q+1 = 7 приведен в показательных частях таблицы 1, сформированных в таблицу 2, в левом столбце которой отмечены индексы m• q+1, где m = 1, 2, 3, ... , а во втором и третьем столбцах отмечены кратные q + чис- ла, индексируемые последовательностями соответственно (m• q+1 + 1) = {8, 22, 29, 36, .„} и

( m • q 6 ⁺ 1 - 2) = {5, 19, 26, 33, _}:

Таблица 2

Пример адресации составных чисел при q 6 ⁺ 1 = 7

k	q + 1	q 6 + k
0	1	5
5	31	35
6	37	41
7	43	47
8	49	53
19	115	119
20	121	125
21	127	131
22	133	137
23	139	143
24	145	149
25	151	155
26	157	161
27	163	167
28	169	173
29	175	179
30	181	185
31	187	191
32	193	197
33	199	203
34	205	209
35	211	215
36	217	221

Для фиксированного q 6 + 5 , в свою очередь, уже другая последовательность ( m • q + 5 - i ), где m = 1, 2, 3, … , индексирует все кратные этому q + 5 составные числа во множестве { q 6 + 1 }, а последовательность ( m • q + 5 + i - 1), где m = 1, 2, +5      _ _

• 3,    ... , индексирует все кратные q₆ i составные числа во множестве { q ₆ ⁺ _k ⁵ }.

Для заданного отрезка [ N_min ; N_max ] из вышеупомянутых последовательностей нужно выбирать те их члены, которые индексируют числа, содержащиеся внутри этого отрезка. Пример для q + 50 = 5 приведен в таблице 3, в левом столбце которой представлены индексы m • q + 50 , где m = 1, 2, 3, .„, а во втором и третьем - кратные q + 5 числа, индексируемые последовательностями соответственно ( m • q + 0 - 1) = {4, 24, 29, 34, ...} и ( m • q +. 0 ) = {5, 25, 30, 35, _}:

Таблица 3

Пример адресации составных чисел при q 6 ^{+ 5} о = 5

k	q 6 + k	q 6 + k
0	1	5
4	25	29
5	31	35
24	145	149
25	151	155
26	157	161
27	163	167
28	169	173
29	175	179
30	181	185
31	187	191
32	193	197
33	199	203
34	205	209
35	211	215

ВЕСТНИК 2013 № 4

Таким образом, если перебрать все подходящие q ⁺ 1 и q ⁺ , то из заданного отрезка [ N min ; N max ] можно отсеять все составные числа и тем самым определить в нем все простые.

Индексный алгоритм произвольного порядка

Сформируем индексный алгоритм произвольного порядка n для нахождения простых чисел в заданном отрезке [ N _min; N _max], обобщив изложенный алгоритм второго порядка.

Применим кольцевую факторизацию для pn# к отрезку [1; Nmax], примем обозначения, аналогичные принятым выше 4+ #.k = pn #• k +1, qpn+k = Pn #•k+Pn+1,

q + k = P n # • ^{k +} P n + s ,

где k = 0, 1, 2, _ k _max (для максимально возможного k = k _max должно быть выполнено условие q ^p1«_t<  N ), и занесем эти данные в таблицу 4:

P n # • k max max

Таблица 4

Индекс	q p„ # • k	+ P n + 1 q P n # • k		z-t + pn + r q Pn # • k		Z-1 + pn + s q Pn # • k
0	1	P n +1		P + + r		Pn + s
1	Pn #-1 + 1	P„ #'1 + P n +1		Pn #•! + P n + r		Pn #•! + Pn + s
k max	P„ # k max + 1	P n #• k max + P n +1		Pn #• k max + P n + r		P n #• k max + P n + s

Результаты кольцевой факторизации для p n # в табличном виде

ВЕСТНИК 2013 № 4

В левом столбце таблицы приведена последовательность индексов 0, 1, 2, ... k _max, в двух других столбцах - отображения этой последовательности в множества вида { p #• k + 1}, { P n #• ^{k +} P n +1 ^} , . { P n #• ^{k +} P n + r ^} , . { P n #• ^{k +} P n + s ^} , содержащие как простые, так и составные числа, а также единицу.

Использованные обозначения: p 1 = 2, p ₂ = = 3, ... p_n - записанные в порядке возрастания простые числа; p n # - примориал (произведение всех простых чисел, меньших либо равных P_n ); p_{n +1}, ... p_{n +} r , ... p_{n +} s - записанные по возрастанию числа из интервала (p_n ; p_n #), являющиеся простыми или всевозможными произведениями простых чисел из этого же интервала; s - количество простых чисел и их произведений на интервале ( p_n ; p_n #); r = 1, 2, 3, . s .

Перейдем к следующему этапу - отсеву оставшихся после кольцевой факторизации составных чисел из множеств {qр’#.k}, {qpp# +k}, ... {q p#+k }, . {q , . +k }, где k = 0, 1 ”2, . kmax. Кратные числу q составные числа можно исключить, вычислив их индексы, для чего обобщим полученные для индексного алгоритма второго порядка соотношения на произвольный порядок. При этом q е {Q} = {Pn#• i + 1} U {Pn#• i + Pn +1} U U ... U {Pn#• i + Pn+r} U ... U {Pn#• i + Pn+s}, где i = = 0, 1, 2, ... imax (для максимально возможного i = imax должно быть выполнено условие (q+V )2 < N ), r = 1, 2, 3, ... s. Чтобы вычис-Pn #• imax          max лить эти индексы, введем для фиксированного q е {Q} числа tj, где j = 1, 2, ... (s + 1). Числа tqj определяются в диапазоне [0; q - 1] и принимают значения из первого столбца таблицы 4 соответственно тому, на какой строке в (j' + + 1)-ом столбце находится кратное q число. Это означает, что для каждого q определяется свой паттерн tj q g{Q}, (1) под которым будем понимать схему размещения кратных q чисел в строках с индексами 0, 1, . (q - 1) таблицы 4.

Покажем, что этот паттерн повторяется в строках с индексами m• q, ... , (m + 1)q - 1, где m = 0, 1, 2, . . Число, стоящее в (/' + 1)-ом столбце таблицы 1 на строке с индексом m • q + tq, (2) при j > 1 равно

P n # ⁽ m • q ^р j ^р P n р j - 1 =

• = P n # • t q ⁺ P n + j - 1 ⁺ P n # • m • q , ⁽³⁾ или (при j = 1)

P n # ⁽ m • q ⁺ j ^{+ 1} = P n # • t q ^{+ 1 +} P n # • m • q , ⁽³ *) а значит, отличается от стоящего в ( j + 1)-ом столбце таблицы 4 на t q -ой строке числа (при j >  ^{1 -} P n # • t q ⁺ P n + j - 1 , ^или при ^j = ^{1 -} P n # • t q ^{+ 1} по определению кратного q ) на p_n # • m • q и, следовательно, делится на q . Очевидно, что для определенного отрезка [ N _min; N _max] из последовательностей (2) нужно выбирать те их члены, которые индексируют числа, содержащиеся внутри этого отрезка в таблице 4.

Рассмотрим в качестве примера отсеивание кратных q = q 3^ = 7 чисел при выполнении индексного алгоритма третьего порядка. Третий порядок индексного алгоритма означает, что нужно взять 3 первых простых числа и перемножить их: 2 х 3 х 5 = 30, после чего составить таблицу кольцевой факторизации, содержащую все простые числа и состоящую из членов прогрессий {30 k + 1}, {30 k + 7}, {30 k + 11}, {30 k + 13},

{30 k + 17}, {30 k + 19}, {30 k + 23}, {30 k + 29}. Для того чтобы отсеять все числа, кратные 7, нужно в диапазоне индексов [0; 6] определить паттерн (1) для числа 7:

t^J_q= {3,0,5,4,2,1,6,3}, для j = 1, ... 8, q = 7. (4)

Далее следует во множестве диапазонов ин- дексов {[7; 13], [14; 20], …} исключить соответственно паттерну (4) кратные 7 числа, которые будут находиться по формуле (2) на тех же местах, что и в диапазоне [0; 6]. Описанный процесс показан в таблице 5, полученной из таблицы 4 при n = 3:

Таблица 5

Пример адресации составных чисел при q = q ₃ ⁺ _м = 7

k	30 k + 1	30 k + 7	30 k + 11	30 k + 13	30 k + 17	30 k + 19	30 k + 23	30 k + 29
0	1	7	11	13	17	19	23	29
1	31	37	41	43	47	49	53	59
2	61	67	71	73	77	79	83	89
3	91	97	101	103	107	109	113	119
4	121	127	131	133	137	139	143	149
5	151	157	161	163	167	169	173	179
6	181	187	191	193	197	199	203	209
7	211	217	221	223	227	229	233	239
8	241	247	251	253	257	259	263	269
9	271	277	281	283	287	289	293	299
10	301	307	311	313	317	319	323	329
11	331	337	341	343	347	349	353	359
12	361	367	371	373	377	379	383	389
13	391	397	401	403	407	409	413	419
14	421	427	431	433	437	439	443	449
15	451	457	461	463	467	469	473	479
16	481	487	491	493	497	499	503	509
17	511	517	521	523	527	529	533	539
18	541	547	551	553	557	559	563	569
19	571	577	581	583	587	589	593	599
20	601	607	611	613	617	619	623	629

ВЕСТНИК 2013 № 4

Если в заданном отрезке [ N _min; N _max] с помощью соответствующих паттернов (1) отсеять составные числа (3) и (3*), кратные всем подходящим q (1), то в нем останутся только простые числа. Отметим, что количество паттернов равно количеству элементов множества { Q }, которое зависит от значения N _max. Следовательно, на отрезках равного размера с различным N _max количество паттернов будет больше у отрезка с большим N _max. Перейдем к исследованию полученного алгоритма.

Результаты

Изложенный алгоритм реализован на языке программирования C++ с использованием библиотеки GMP для работы с большими числами и проверен на совпадение результатов генерации с первыми 50 миллионами простых чисел [5]. Индексные алгоритмы второго, третьего и четвертого порядков исследовались на время работы при различных отрезках и различных нижних грани- цах на компьютере с процессором Intel Core i3 2,93 ГГц. Увеличившееся время работы по сравнению с [4] обусловлено 64-битным представлением чисел в упомянутой статье. Использование представления mpz_t из GMP позволяет судить о поведении алгоритмов за пределом 64-битного представления.

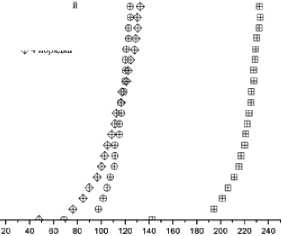
На рис. 2–5 представлены результаты работы алгоритмов для отрезков, указанных в подписях. Из рис. 2 видно, что для миллионного отрезка индексный алгоритм второго порядка работает быстрее остальных, а четвертого – сильно отстает. Однако уже на отрезке 5∙107 (рис. 3) видно, что индексный алгоритм третьего порядка по времени работы практически сравнялся по скорости с алгоритмом второго, а на больших отрезках – стал быстрее. Аналогичная ситуация повторяется на отрезке 109 (рис. 4): индексный алгоритм четвертого порядка по времени работы сравнялся с индексным алгоритмом третьего порядка, а на отрезке 4∙109 (рис. 5) – стал быстрее.

1,806+015-

1,606+015-

| 1,406+015-

|" 1,206*015- я 1,006*015-

I 8,006*014-

* 6,006+014-

I 4,006*014-

2,006*014 -

В ф вф а® в е шф

ЕФ

Ж

®

@

® ф

Индексныйф алгоритм*

В 2 порядка

Ф

Ф

Ф

Ф

Ф

Ф

Ф

Ф

0.006+000

20 М 40   50   60 70 80   90 100 110

Время [секунды]

Время [секунды]

Рис. 2. Сравнение скоростей работы индексных алгоритмов генерации простых чисел на отрезке размером 10 ⁶ (считая от значения ординаты)

Рис. 3. Сравнение скоростей работы индексных алгоритмов генерации простых чисел на отрезке размером 5∙10 ⁷ (считая от значения ординаты)

ВЕСТНИК 2013 № 4

6,006*014-5,406+014-

§ 4.80Е+014-а             '

Cl 4,206+0145 3,606+014-_ 3,006+014-О. 2,406*014-| 1,806+014- = 1,206+014-

6,006*013-

Индексный алгоритм £ 2 порядка ®3 порядка ф4 порядка

Время [секунды]

0,006+000

Рис. 4. Сравнение скоростей работы индексных алгоритмов генерации простых чисел на отрезке размером 10 ⁹ (считая от значения ординаты)

Таким образом, для бóльших отрезков индексные алгоритмы генерации простых чисел большего порядка работают лучше, чем для меньших. Напротив, для меньших отрезков индексные алгоритмы генерации простых чисел меньшего порядка работают лучше, чем для бóльших. Происходит это потому, что для большего отрезка увеличивается время определения соответствующих ему паттернов, согласно которым отсеиваются составные числа. Для меньшего отрезка наблюдается обратная ситуация – паттерны находятся быстрее.

Выводы

Индексный алгоритм в его текущей реализации представляет принципиально новый подход к поиску простых чисел. Однако требуется его оптимизация применительно к объему кэш-памяти используемого процессора. В то же время, индексный алгоритм с использованием кольцевой факторизации нетребователен к вычислительным ресурсам, поскольку он оперирует с булевым массивом. Благодаря своей многозадачной структуре алгоритм легко моди-

1,606+014-]

1,406*014-

| 1.206+014

£ 1,006+014

2 8,006+013

£- 6,006+013-

| 4,006+013

1 2,006+013

0,006+000- -

ф ^       Индексный щ

.                  алгоритм

$2 порядка Ф    *     ФЗпорщка»

ф    ®     ф» порядкаS ф   Фш ф   фщ ф   фS ф   ®ш ф     Фffi ф   @ш ф   Фв ф   ®в ф фш ф ®в ф фв

I ■ I ^ I .........*.....

10О 200   300   400   500   600   700   800   9001000

Время [секунды]

Рис. 5. Сравнение скоростей работы индексных алгоритмов генерации простых чисел на отрезке размером 4∙10 ⁹ (считая от значения ординаты) фицируется как многопоточный с реализацией на GPU.