Индуктивное обобщение данных на основе антиципации

Введение1

Под интеллектуальным2 анализом данных понимается процесс3 поддержки принятия решений, основанный на поиске в данных скрытых закономерностей [1]. Задачи обработки экспериментальных данных всегда зависят от некоторой концептуальной схемы, в рамках которой выдвигаются определенные гипотезы относительно изучаемого объекта и цели эксперимента. В качестве такой концептуальной схемы в настоящей работе используется теория функциональных систем, предложенная П.К. Анохиным [2]. В частности, речь идет об использовании свойства антиципации при анализе данных, которые являются определяющими в поведении людей, социальных групп, популяций и т.д. В основу анализа данных, выступающих в качестве свойств некоторого объекта и являющихся характерными для описания его поведения, положена гипотеза о том, что изменение значений таких свойств является подготовкой к будущим состояниям самого объекта или внешней среды. Подобная особенность поведения называется опережающим отражением, или антиципацией. При формализации задачи анализа данных с подобным свойством важна динамика наблюдаемых значений и фиксация момента, когда значения существенно изменяются либо на основе прогноза результатов собственных действий объекта, либо при изменении цели, диктуемой внешней средой.

В последнее время неуклонно растет интерес к методам обнаружения знаний в базах данных (Knowledge Discovery in Databases) и обработки (раскопки) данных (Data Mining). Объемы современных баз данных, которые весьма внушительны, вызвали устойчивый спрос на новые алгоритмы анализа данных. Одним из популярных методов обнаружения знаний стали алгоритмы поиска ассоциативных правил. Ассоциативные правила позволяют находить закономерности между связанными событиями.

Задачу синтеза ассоциативных правил будем рассматривать в следующей постановке. Пусть дана выборка объектов, причем для каждого объекта из выборки известно – обладает он некоторым свойством или нет. Предъявляются объекты из другой выборки. Требуется получить правдоподобные гипотезы относительно обладания этими объектами ранее зафиксированных свойств. Для упрощения формулировки задачи будем считать, что объект описывается двумя признаками. Для некоторого признака A известна совокупность свойств, которыми он может обладать. Другой признак - B - представлен только значениями (измерениями). Предполагается зависимость свойств признаков, причем объект обладает следующей особенностью: возможно изменение свойства одного признака до изменения свойства другого признака. Объект как бы настраивается на изменение своего состояния. Подобная особенность поведения объекта известна в физиологии и названа принципом антиципации поведения (опережающее отражение). Необходимо, с учетом антиципации поведения объекта, в процессе одновременного наблюдения значений обоих признаков выделить неизвестные свойства признака B, а также влияние свойств признака B на свойства признака A.

Процесс поиска правил включает несколько этапов: накопление сырых данных, обобщение и преобразование данных, поиск закономерностей в данных, оценка, обобщение и структурирование найденных закономерностей. В данной работе рассматривается подход к обобщению данных и преобразование некоторых их совокупностей в форму нечетких множеств. Такой подход позволяет осуществить переход от отдельных числовых значений, характеризующих свойства объекта или системы, к интервалам, каждое значение которого определяется нечеткой степенью его принадлежности некоторому свойству. Необходимость применения методов обобщения информации в интеллектуальных системах обусловлена как построением обобщенных моделей данных, так и обработкой больших массивов экспериментальных данных, полученных в ходе различного рода процессов и явлений. С помощью методов обобщения выделяются признаки, характеризующие группу, к которой принадлежит тот или иной объект, и выявляются новые, нетривиальные и полезные знания.

1.    Интервальный анализ данных

Рассмотрим базу данных с числовыми значениями, относящимися к различным характеристикам (свойствам, атрибутам) объекта. Задача состоит в поиске закономерностей между свойствами объекта и некоторым заключением относительно рассматриваемого объекта, например управляющего решения, изменяющего его состояние, принадлежности объекта к некоторому классу и т.п. Другими словами, задача состоит в построении правил типа «если X есть A, то Y есть B». Неопределенность решения состоит в том, что заранее известны либо вербальные описания атрибутов X, либо их число, характеризующих заключение Y. Например, для задачи классификации рассмотрим объект X с атрибутами {Xр X,}={возраст, уровень дохода}. Тогда лингвистические метки (значения), характерные для X1 и X2, могут быть следующими: A^{молодой, средний, пожилой} и A2={низкий, высокий}, а B = {класс 1, класс 2, класс 3}.

Пусть, E ={ e ₁, e ₂, ..., e N } - база данных с N записями (транзакциями). Запись e i (i е T = 1, N ) -является множест вом значений a ij атрибутов (параметров), j = 1, т , т.е. e i = { а _ц,..., a i _т }, где т - число атрибутов (параметров) признака A . Здесь T определяет последовательные моменты времени синхронно фиксируемых параметров. Будем считать, что a i , ,..., a im _{- 1} являются числовыми данными, а a im - качественное значение, характеризующее свойства признака A . Для определенности, положим, что A m = { p _p..., p q }, т.е. a 1, m ^е{ P 1 >-> P q ^} .

Рассмотрим задачу преобразования числовых данных a i j , j = 1, т - 1 в совокупность интервалов, связанных со свойствами a im . Для простоты изложения будем рассматривать два атрибута. Пусть a , j , a i ₊ 1, j , a , m , a i ₊ 1, m значения атрибутов A j и A m , зафиксированные в последовательные моменты времени i и i + 1, причем a i m = a i _{+ 1 т} . Для признака A m известна совокупность свойств p ₁,..., p q , которыми он может обладать. Другой признак A_j представлен только значениями (измерениями). Предполагается зависимость свойств признаков, причем объект обладает следующей особенностью: возможно изменение свойства одного признака до изменения свойства другого признака. Необходимо, с учетом антиципации поведения объекта, в процессе одновременного наблюдения значений обоих признаков выделить неизвестные свойства признака A_j , а также влияние свойств признака A_j на свойства признака A m .

Примем значения a ij , a i _{+ 1 j} за точки плана эксперимента на интервале int₁ = [ c d 1 ], границы которого неизвестны. Тогда, в соответствии с [3], границы интервала можно вычислить из следующих уравнений:

f a, j = c + ( c - d 1 ) ^

I ai+u = d 1 - (d 1 - c1K (1) F где £ = k-Vp , а Fk = Fk-1 + Fk-2 - числа Фибо-Fk наччи для к > 1, причем к выбирается достаточно большим.

ВЕСТНИК 2013 № 4

ВЕСТНИК 2013 № 4

Пусть a_i,m = a_{i +1, m} = p_k .

Определение 1. Выражение вида p k >  int₁, k = 1, q , где p k наблюдается одновременно с a i _j и a i _{+ 1 j} , назовем эмпирической гипотезой 1-го рода.

Пусть Δ t – прогнозируемый интервал времени (порог антиципации), в течение которого изменяется значение атрибута a i _{+д t} m при условии, что a i +Д t , j ^t int j .

Определение 2. Значение атрибута a i _{+ 2} j t ^t int j при условиях a i,m = a i + j m = a + 2m = P k и a +Д t , m * P k , а также значение атрибута ^a i ₊ 2, m * P k при условиях a i j , a i _{+ 1 j} e int 1 и a i _{+д tj} t int 1 назовем антиципациями.

Определение 3. Если a i _{+ 2} j является антиципацией по отношению к некоторому a_{i +д t m} ^ p_k , то выражение вида a i _{+ 2} j > ₂ a i _{+д t m} назовем эмпирической гипотезой 2-го рода.

Утверждение 1. Если a i _{+ 2j} - антиципация по отношению к a i _{+д t m} = p_{k + 1}, то эмпирическая гипотеза 2-го рода имеет интервальный характер вида [ c ₂, d 2 ] > . p_{k + 1}, причем a_{i + 2} , j e [ c ₂, d ₂].

Доказательство. Если a i _{+ 2} j t int 1 - антиципация, то в течение времени Δ t значение p_k изменилось на значение p_{k + 1}. Тогда, как и раньше, значения a i ₊ 2 j , a i _{+ 3} j являются точками плана эксперимента на интервале int₂ = [ c ₂, d ₂], границы которого определяются при решении системы уравнений:

/ a i + 2, j = c 2 + ( c 2 — d 2 ) ^

_ a + з, j = ^d 2 ^{- ( d} 2 ^{- c} 2 ) 5 .

Утверждение 2. Если p_{k + 1} - антиципация по отношению к a_ij , a i _{+ 1 j} e int₁, то эмпирическая гипотеза 1-го рода имеет интервальный характер вида P k + 1 >  ^{[ c} 3 , ^d 3 ].

Доказательство. Пусть a i _{+ 2 m} = p_{k + 1} - антиципация. Это означает, что в течение времени Д t значения a i _j , a i _{+ 1 j} e int 1 изменились на значение a i _{+д t j} t int 1 . Определим границы интервала int₃ = [ c 3 , d 3 ] относительно точек плана эксперимента a i _{+д t j} , a i _{+д t + 1 j} . Тогда гипотеза примет вид: p k + 1 > 1 ^{[ c} 3 , ^d 3 ]•

Таким образом, при анализе базы данных можно сформировать два вида гипотез: int v ( j ) > 2 P f и P f >  int v ( j ), где v - число интервалов значений j -го атрибута, а f = 1, q .

Утверждение 3. Если на некотором временном интервале д t определен интервал int₁( j ) значений j -го атрибута и антиципации отсутствуют, то интервал int₁ ( j ) может быть расширен до интервала int( j ), причем int 1 ( j ) с int( j ).

Доказательство. Пусть на основе измерений a i _j и a i _{+ 1 j} сформирована гипотеза P_k >  int 1 = = [ c ₁, d 1 ], а значение a i _{+ 2 j} t int 1 и не является

антиципацией. Рассмотрим две точки плана экс-c, + d, / перимента 1 V2 и ai+2 j. Определим границы интервала int = [c, d] на основе решения системы уравнений:

c ^{j + d}vL = c + ( c - d ) ^

1          '2

a_t + 2j = d — ( d — c ) £ .

Возможны следующие варианты значений ^a i + 2, j .

¹ a + 2, j >  d 1 .

В этом случае имеем:

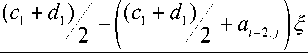
(1 - 2 ^ )

= 2 c ₁ + 2 d ₁ - 2 ^ d ₁ - 1.6 a i _{+ 2 j} = c ₁ + d ₁ - 1.6 a i _{+ 2}

Пусть a i _{+ 2 j} = d ₁ + e . Тогда c = c ₁ + d ₁ - 1.6 d ₁ -- 1.6 e = c ₁ - 0.6 d ₁ - 1.6 e . Очевидно, что lim c = = c ₁ - 0.6 d ₁, т.е. c <  c ₁. ^e > 0

Определим значение правой границы int = [ c , d ]:

⁽ c ^{1 + d 1})/ - c (1 - ^ )

d =------—---------= 2.3 d, - 0.3 c + 2.5 e .

^                              ¹

Очевидно, что lim d ₁ >  d и lim d > да .

c1 > d             e >да e >0

Таким образом, интервалу int = [c, d] при надлежит как [c1, d 1], так и значение ai+2 j.

2. a i + 2, j <  ^c 1 .

Имеем:

a -{a   + (c1+d 1)/V ai+2, j    ai+2, j +         /2 ^

c =-------------------—

(1 - 2 ^ )

= 4.2 a + 2, j

-

- 4.2 a i _{+ 2}, _j ^ - 0.8 c ₁ - 0.8 d ₁ = 2.6 a_+2j - 0.8 c ₁ - 0.8 d ₁ .

Пусть a i _{+ 2 j} = c ₁ - e . Тогда c = 2.6 c ₁ - 2.6 e -- 0.8 c ₁ - 0.8 d ₁ = 1.8 c ₁ - 0.8 d ₁ - 2.6 e и lim c >  c₁ , e > 0

lim c >-да .                             d 1 >  c 1

^e >^v Оценим значение правой границы:

d =

^a i + 2, j

-

c ₁

^

(1 - ^ )

= 2.6 a i + 2, j

- 1.6 c =

= 1.3 c ₁ + 1.3 d ₁ - 1.4 a_{i + 2}

Пусть a i _{+ 2 j} = c ₁ - e . Тогда d = 1.3 c ₁ + 1.3 d ₁ -

- 1.4 c , + 1.4 e = 1.3 d, - 0.1 c , + 1.4 e и lim d >  1.2 d, , ^{1                                   1                 1}                           e > 0                           ¹

€1 > d lim d > да. В обоих случаях d > d 1.

e >да

Следовательно, при a i _{+ 2 j} <  c₁ ^int 1 ^{( j} ) ^{с int( j} ) и a i + 2,j ^{e int( j} ) .

Пусть R – множество всех вещественных чисел, а int₁ = [ c ₁, d ₁] и int₂ = [ c ₂, d ₂] – интервалы.

Определение 4. Интервалы int₁ и int₂ называются подобными, если ρ (int₁, int₂) ≤ α , где ρ (int₁, int₂) = max( c ₁ - c ₂), d ₁ - d ₂) , α – заданное вещественное число.

Определение 5. int₁ <  int₂тогда и только тогда, когда c ₁ < c ₂ и d ₁ < d ₂.

Определение 6. Если интервалы int₁ и int₂ подобны, то их обобщением является интервал int = int 1 U int₂.

Определения 4–6 позволяют, с одной стороны, удалить избыточные интервалы, с другой, – упорядочить интервалы, сформированные после обобщения.

2.    Лингвистическое обобщение интервалов

Пусть в результате анализа базы данных для каждого j-го атрибута сформированы интервалы int1, int2, …, intn, причем int1 < int2 < … < intn. Построим на каждом интервале нечеткие множества вида Ah =< µν /{ah(t)}>,h= 1,n, где ah(t) ∈inth; µν(ah(t))= nn∗ – функции принадлежности, где n – число ah (t), удовлетворяющих предикату ah(t) →2 pk; n* – общее число наблюдений pk . В соответствии с [4] функция µν является точечной детерминацией предиката →2 . Аналогично определим точечные детерминации предикатов типа →1 , обозначив ∑nν их через ϑw = ν ∗ , где ∑nν - количество ah(t), удовлетворяющих предνикату pk→1 ah(t). Построенные описанным выше способом нечеткие множества позволяют перейти к более общим описаниям предикатов →1 и →2 , которые будут иметь вид: x∈Ajpk→1 x, x∈Ajx→2 pk. При переходе от точечной детерминации ϑw к кванторам, в соответствии с методикой их определения в [4], предикаты типа →2 будут иметь вид: Δx∈Ajx→2 pk, где Δ – нечеткий квантор. Величина Aj является интервальным обобщением наблюдений и интерпретируется как нечеткая переменная.

Определение 7. Нечеткие переменные A_h и A_s назовем совпадающими, если A_h ≅ A_s для всех A_h → ₂ p_k и A_s → ₁ p_k . Здесь ≅ – операция нечеткого равенства, определяемая в соответствии с [5].

Операцией совмещения нечетких переменных Ah и As назовем операцию пересечения нечетких подмножеств Ah П As, если нечеткие переменные Ah и As являются совпадающими. Использование операции пересечения нечетких подмножеств позволяет избавиться от избыточной информации в наблюдениях и уменьшить число анализируемых гипотез.

С целью формирования правдоподобных гипотез введем порог детерминации ϑ _w . Если ϑ _w ∈ [0.6, 1], то наблюдение рассматривается в качестве гипотезы с правдоподобием, равным ϑ _w . Если ϑ _W ∈ [0, 0.6] , то будем считать, что данных недостаточно для формирования гипотезы о влиянии свойств одного признака на свойства другого.

Результаты интервальной обработки данных характеризуются следующими особенностями:

• –    интервалы значений атрибутов могут быть пересекающимися;

• –    сформированные гипотезы могут быть противоречивыми;

  – число сформированных интервалов по каждому атрибуту можно интерпретировать как число кластеров, на которые разбиваются множества значений атрибутов.

В силу первой особенности при формировании правил корректно интерпретировать интервалы как лингвистические значения атрибутов, представленные соответствующими нечеткими множествами.

Противоречие гипотез следует из анализа набора бинарных данных. В качестве примера рассмотрим гипотезы, сформированные на основе бинарного анализа:

• 1.    A → C ;

• 2.    A → B ;

• 3.    B → A ;

• 4.    B → D .

Гипотезы 2 и 3 противоречат друг другу. Для разрешения подобного противоречия возможны следующие решения [6]:

– оперативный анализ данных в процессе деятельности с учетом возможных антиципаций;

– при формировании гипотез и правил необходимо учитывать время переходных процессов от одного интервала к другому или, иначе говоря, логику времени, в рамках которой можно было пользоваться такими понятиями, как «в начале деятельности», «вскоре после этого», «по окончании решения задачи» и т.п.;

– при формировании гипотез следует учитывать не бинарные, а многомерные отношения между значениями атрибутов.

Для перехода от гипотез к правилам необходимо перейти от интервальных значений атрибутов к лингвистическим значениям, а затем относительно лингвистических значений атрибутов формировать соответствующие правила.

ВЕСТНИК 2013 № 4

ВЕСТНИК 2013 № 4

Первым шагом для формирования лингвистических значений атрибутов является выделение характерных значений для каждого атрибута. Данная задача решается алгоритмами кластерного анализа. В случае наличия интервалов изменения значений для каждого атрибута такая задача может быть решена более корректно. Во-первых, число интервалов определяет число кластеров. Во-вторых, первоначальные центры кластеров задаются непроизвольно: в качестве центров можно назначить средние величины тех значений каждого интервала, которые присутствуют в базе данных. Такой подход оптимизирует процедуру кластерного анализа за счет уменьшения числа вычислений.

Обобщенная процедура перехода от интервальных гипотез к лингвистическим правилам определяется следующими шагами.

• 1.    При реализации алгоритма поиска закономерностей в соответствии с введенными определениями и операциями интервальной математики вначале выделяется упорядоченная совокупность интервалов для каждого атрибута. Их формирование было необходимо для вычисления числа кластеров j- го атрибута, которое априори неизвестно, и обоснования применения процедуры кластерного анализа для получения центров кластеров с целью перехода от количественных интервалов к лингвистическим значениям.

• 2.    На втором этапе используется процедура кластерного анализа, в результате которой определяются центры кластеров, интерпретируемые как характерные значения нечетких множеств.

• 3.    На третьем этапе формируются пересекающиеся интервалы нечетких множеств каждого атрибута. Нечеткие множества интерпретируются как лингвистические свойства соответствующего атрибута.

• 4.    Далее осуществляется формальное построение нечетких множеств и экспертным путем определяется лингвистическая семантика нечетких множеств.

В процессе построения на первом этапе интервалов одновременно формируются эмпирические гипотезы, определяющие бинарные отношения между атрибутами. Последним этапом является формирование возможных и значимых бинарных правил между лингвистическими значениями атрибутов.

Подобная процедура повторяется для каждой пары атрибутов. Для окончательного формирования набора правил анализируются противоречия в правилах, возникающие из-за бинарного характера анализа на основе предыдущей процедуры, за счет перехода к анализу многомерных отношений.

Заключение

Рассмотренный подход к формированию правдоподобных гипотез и индуктивному обобщению последовательности измерений в форме нечетких множеств (нечетких переменных) позволяет осуществить анализ баз данных объектов, для которых характерно свойство антиципации поведения. Данный подход ориентирован на анализ баз данных с неизвестными закономерностями между значениями количественных и качественных атрибутов и позволяет формировать правдоподобные гипотезы с оценкой их достоверности в процессе наблюдений.