Индуктивный метод определения диэлектрических свойств жидкостей

Представления о диэлектрической проницаемости £ веществ на частотах менее 100 МГц базируются на экспериментальных данных, полученных емкостным методом (C-методом), в котором исследуемый объект помещается в измерительный конденсатор (C-ячейку). Найденные C-методом значения £ C жидкостей в указанном диапазоне частот постоянны и равны статической диэлектрической проницаемости. Попытки выявления низкочастотной дисперсии £ C жидкостей не выдерживают критики [1, 2]. Однако отсутствие дисперсии £ C в воде, спиртах и их растворах является одним из парадоксов диэлькометрии, т. к. противоречит существованию в этих жидкостях кластеров и сольватированных ассоциатов, выявляемых другими методами [3].

Указанное противоречие снимается при исследовании диэлектрических свойств ассоциированных жидкостей индуктивным диэлектрическим методом (L-методом), в котором жидкость вместо конденсатора помещается в катушки индуктивности (L-ячейки) [4, 5]. Суть метода демонстрирует рис. 1 (кривые 1, 2), согласно которому ввод диэлектрического сосуда с жидкостью внутрь L-ячейки, подключенной к колебательному контуру куметра, уменьшает добротность Q и емкость С контура при резонансе. Несмотря на то что это явление давно известно и используется в электрохимии для бесконтактной кондуктометрии (смотри обзоры [6–10]), его природа осталась неясной.

РАЗРАБОТКА ТЕОРИИ МЕТОДА

С целью выяснения причины представленного на рис. 1 явления и его особого значения для ди-элькометрии рассмотрим колебательный контур, в котором измерительная соленоидальная L-ячейка с индуктивностью L и активным сопротивлением R последовательно соединена с калиброванным конденсатором переменной емкости C, с помощью которого контур настраивается на резонанс. Условием резонанса такого контура с добротностью Q = toL / R является:

ю ²

1      R ²            1

---:---:— .

LC 4 L ² LC (1 + 1/4 Q 2 )

Из (1) получаем, что при Q > 20 величина сдвига резонансной емкости за счет снижения добротности контура при введении жидкости в L-ячейку близка к точности ее определения. Тогда, пренебрегая в (1) при Q > 20 вкладом от величины Q, но, учитывая, что L-ячейка имеет межвитковую собственную емкость Co, условие резонанса контура получаем в виде to2 = 1/L (C + C0).                 (2)

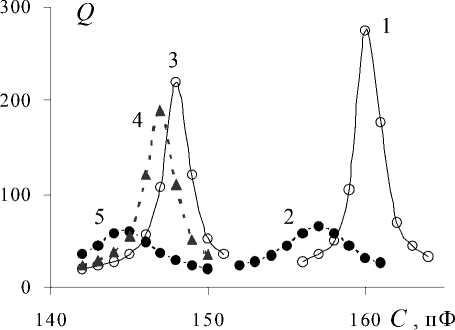
Рис. 1. Резонансные кривые колебательного контура куметра TESLA BM-311 на частоте 2 МГц с ячейкой L₁ (1 — без воды, 2 — с водой); совместном подключении ячеек L₁ и L₂ (3 — обе ячейки без воды, 4 — вода в L₂, 5 — вода в L₁). Во все ячейки вводится одна и та же порция воды в стеклянной пробирке

Из (2) следует, что сдвиг резонансной емкости после внесения жидкости в L-ячейку может происходить либо из-за увеличения C 0 (емкостной принцип работы ячейки), либо L (индуктивный принцип работы ячейки).

Эксперимент

Для выяснения принципа работы L-ячейки, сопоставим чувствительность двух L-ячеек к вводу одной и той же порции воды. В качестве первой ячейки (ячейка L₁) рассмотрим соленоидальную катушку, в качестве второй (ячейка L 2 ) — соленоидальную катушку идентичного размера и тем же числом витков, но с коллинеарной обмоткой. При коллинеарной обмотке индуктивность ячейки многократно снижается, а собственная емкость наоборот увеличивается. Последовательно соединенные обе ячейки подключим к куметру и по очереди внесем в них пробирку с водой. Как видно на рис. 1 (кривые 3–5), изменения добротности и резонансной емкости при вводе воды оказываются существенно больше у ячейки L₁. Этот факт свидетельствует, что внесение воды в исследуемые L-ячейки меняет ее параметры преимущественно по индуктивному механизму. В случае емкостного механизма более заметные изменения параметров должны были бы наблюдаться у ячейки L 2 .

Анализ эксперимента

То, что принцип работы L-ячеек обусловлен индуктивным механизмом, полагается и в [6–10]. Причем изменение индуктивного toА L и активного А R сопротивления L-ячейки объясняется возникновением в жидкости вихревых токов. Для выяснения действительной причины влияния жидкости на индуктивность L-ячейки рассмотрим найденные из уравнений Максвелла выражения для амплитудного значения магнитной индукции и магнитного потока внутри бесконечно длинной цилиндрической L-ячейки, заполненной жидкостью с диэлектрической проницаемостью е , магнитной проницаемостью ц = 1 и удельной электропроводностью χ :

B = В о J о ( ar )/ J о ( ar o );

Ф = 2Ф о J 1(aro) / ar0 J о(ar0), где B0 — напряженность переменного магнитного поля внутри L-ячейки без жидкости; to — его частота; a2 = ^to(Eto -i%); J0(ar) и J 1(ar) — функции Бесселя; r0 — радиус пробы жидкости; Ф0 = B0 nr02. После разложения функций Бесселя в ряд и избавления от комплексных величин оказывается, что изменение магнитного потока внутри ячейки после помещения в нее жидкости преимущественно определяется лишь двумя слагаемыми:

( 1                    51

А Ф = Ф о\- r о Ц^{Eto -} —ro ^^to% | =

I 8            384

= АФ1 -АФ 2.(3)

Первое слагаемое в (3) связано с возникновением в жидкости токов смещения, зависящих от ее диэлектрической проницаемости е второе — вихревых токов, пропорциональных χ ². Т.о. использование L-ячейки для кондуктометрии правомерно тогда, когда А Ф ₂ >>  А Ф 1 , а для диэлькометрии — при А Ф 1 >>  А Ф ₂. Для чистой воды отношение А Ф 1 / А Ф ₂ ~ 10⁹. Поэтому для жидкостей и их растворов с х <  X max более правомерно диэлькомет-рическое применение L-ячеек. Величину X max предлагается оценивать из условия

А Ф ₂/ А Ф 1 = 5 r O ц% ²/48 е <  0.05.         (4)

Для водных растворов с r ₀ = 1.5 см X _max = 10 мСм/см (соответствует примерно 1% раствору NaCl). Полагая, что для жидкостей с X < X _max относительное изменение индуктивности L-ячейки после ввода жидкости равно относительному изменению магнитного потока за счет токов смещения, находим величину Δ C :

А C = E S о IE m _a x /2( UQ 1 ) 2 = е / а,           (5)

где α =2( UQ ₁)² / lE _m ² _ax S ₀ — есть постоянная измерительной ячейки; E _max= to B ₀ r /2 — максимальная напряженность электрического поля внутри L-ячейки радиусом r; U — напряжение, подаваемое на вход контура и не меняющееся во время измерений; l — длина обмотки ячейки; S 0 = п r ₀² — площадь сечения пробы жидкости в L-ячейке [4, 5].

Соотношение (5) подтверждается линейной зависимостью величины Δ C от диэлектрической проницаемости е жидкости (рис. 2), а также независимостью значений Δ C немагнитных жидкостей с X <  X _max от индуктивности L-ячеек одинакового размера.

МЕТОДИКА ИНДУКТИВНОГО (L-) МЕТОДА

Определив по уравнению линии тренда калибровочной зависимости А C сосуда с жидкостью от е жидкости постоянную α ячейки, а также величину

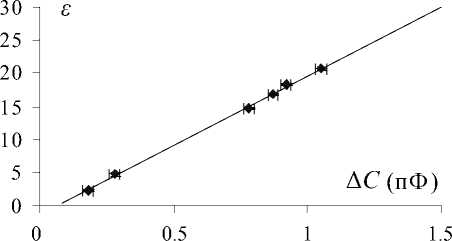
Рис. 2. Пример калибровочной зависимости ε (Δ C ) для L-ячейки, полученной на примере ксилола, хлороформа, изоамилового спирта, циклогексанола, изопропанола и ацетона

Δ C * от ввода пустого сосуда, можно находить значения ε _L жидкостей (индекс "L" указывает на метод определения ε ):

£ l = a (A C — A C *).              (6)

Величина тангенса угла диэлектрических потерь (tg δ ) объектов L-методом определяется по изменению активного Δ R и индуктивного ω Δ L сопротивления L-ячейки после их ввода: tg δ = Δ R / ω Δ L . Значения Δ R и ω Δ L находятся из соотношений:

L0=1/ω2(C1+C0),(7)

L0 +∆L=1/ω2(C2 +C0),(8)

Q1=ωL0/R0=Qf1(1+C0/C1),(9)

Q ₂ = ω ( L ₀ + ∆ L ) /( R ₀ +∆ R ) =

= Qf2 (1 + C0 /C2),(10)

где R ₀ и ω L ₀ — активное и индуктивное сопротивления ячейки без жидкости, С 1 , С 2 , Q 1 , Q 2 — значения емкости калиброванного конденсатора и добротности колебательного контура куметра при резонансе до ( С 1 , Q 1 ) и после ( С 2 , Q 2 ) введения вещества в L-ячейку. Значения Q 1 , Q 2 соотношениями (9, 10) связаны с так называемыми множителями вольтажа Q_{f 1} , Q_{f 2} , отсчитываемыми при резонансе по шкале вольтметра, измеряющего напряжение на калиброванном конденсаторе. Из (7–10) находим, что

СQ_f .(1 + C / C ) 2 - CQ ₂(1 + С / C ₂)²

1 f 1           0      1           2 f 2           0      2

tg δ =                                           . (11)

( C 1 - C 2 ) Q f 1 Q f 2 (1 + C 0 / C 1 )(1 + C 0 / C 2 )

При C 0 =0 значения Q_{f 1,2} = Q _1,2 , и выражение (11) упрощается:

tg § = ( Q i C i - Q 2 C 2 )/ Q i Q 2 ( C 1 - C 2 ).      (12)

При расчете по (11) и (12) значений tg δ различных жидких растворов даже для ячеек с максимальной C ₀ = 10 пФ обнаружено совпадение полученных данных с точностью выше ошибки эксперимента. Этот факт подтверждает пренебрежимо малую роль емкостного механизма в принципе действия L-ячеек и обосновывает применимость для расчета tg δ соотношения (12), использованного ранее в [11, 12].

Поскольку с каждой измерительной ячейкой условие резонанса (2) фиксируется лишь в узком диапазоне частот, то для измерения частотных зависимостей tg δ и ε L объектов необходим комплект измерительных L-ячеек одинакового геометрического размера. Во избежание артефактов при таких исследованиях L-ячейки должны изготавливаться с перекрывающимися частотными диапазонами, причем различие найденных на двух ячейках значений tg S * и A C немагнитных объектов с χ <  χ _max не должно превышать ~3 % экспериментальную погрешность. Оказалось, что для этого необходимо, чтобы напряженность Е max внутри ячеек удовлетворяла условию

5 мкВ/см <  Е < 200 мкВ/см.        (13)

max

ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ

Достоинства и возможности индуктивного метода для исследования полярных жидкостей продемонстрируем на примере растворов CH 3 COONa в изопропаноле. Найденное по разработанной методике значение ε L абсолютизированного 99.95 % образца изопропанола, полученного по методике [13], в диапазоне частот 200 кГц–5 МГц с 3 % экспериментальной погрешностью совпало с табличным значением статической диэлектрической проницаемости ε C изопропанола (рис. 3). Слабая (менее 30 %) дисперсия ε L изопропанола на частотах менее 200 кГц не сопровождается появлением максимума tg δ , и, возможно, обусловлена малой примесью воды.

Резкое увеличение дисперсии ε _L и появление низкочастотного максимума tg d в изопропаноле обнаружены после растворения в нем солей, например предварительно осушенного CH 3 COONa. Предельно возможное повышение ε L = ε _max на частотах 15–20 кГц в растворе CH 3 COONa наблюдалось при концентрации ∼ 5 ⋅ 10^–3моль/л. При этом значение ε L = ε _min растворов на частотах, выше 1 МГц, оставалось близко к ε L чистого спирта.

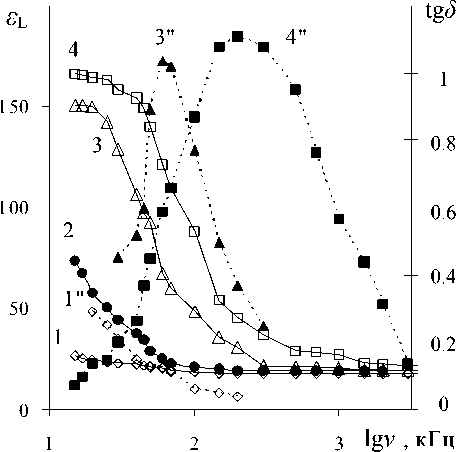
Рис. 3. Частотные зависимости ε _L (1–4) и tg δ (1", 3", 4") для растворов CH₃COONa в изопропаноле с концентрацией: 1, 1" — 0 %; 2 — 10^–4моль/л; 3, 3" — 10^–3моль/л; 4, 4" — 5 ⋅ 10^–3моль/л

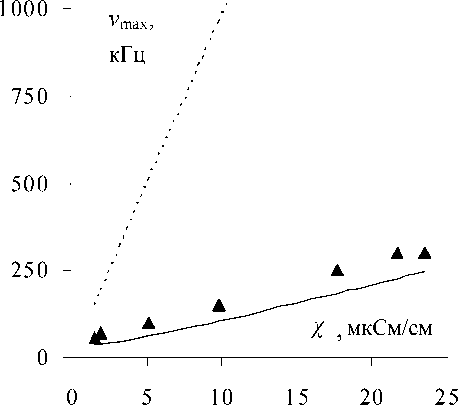
Рис. 4. Зависимость частоты ν _max от χ растворов CH 3 COONa в изопропаноле: ▲ — эксперимент, линии — расчет по (14) при ε = ε _с (пунктир) и ε = ε _max (сплошная линия)

Представленные на рис. 3 данные впервые экспериментально подтверждают теорию Дебая [14]. В [14] было теоретически предсказано, что на частоте ν _i = 1/2 πτ _i , где τ _i — время восстановления атмосферы иона после его перемещения, в растворах электролитов должна наблюдаться низкочастотная дисперсия диэлектрической проницаемости. Полученное Дебаем выражение для τ _i можно представить в виде τ i = ε ₀ ε / χ , где χ — удельная электропроводность раствора, ε — диэлектрическая проницаемость растворителя, ε ₀ — электрическая постоянная. Тогда

ν _i = 1/2 πτ _i = χ /2 πε ₀ ε .        (14)

Как видно на рис. 4, отличие ν _max от ν _i для исследованных спиртовых растворов становится особенно мало, если полагать, что в соотношении (14) ε равно ε _max данного раствора, а не ε с . Достаточно хорошее совпадение ν _max и ν _i при ε = ε _max фактически подтверждает и правильность найденных значений ε . max

Однако при хорошем совпадении ν _max и ν _i величина экспериментально найденной низкочастотной дисперсии ∆ ε _L = ε _max – ε _min оказывается на два порядка больше, чем предсказывается теорией

Дебая ( ∆ ε _D ). Полагается, что существенное различие ∆ ε _D и ∆ ε _L обусловлено тем, что величина ∆ ε _D Дебаем рассчитывалась для ионных облаков, состоящих из ионов противоположного знака. Для рассмотренных в данной работе растворов малой концентрации ближайшее окружение иона состоит из полярных молекул растворителя, ориентированных электростатическим полем этого иона. Релаксация такой ионной атмосферы должна сопровождаться более сильной дисперсией ε .

СРАВНЕНИЕ С- И L-СПОСОБОВ

Для выяснения причины отсутствия низкочастотной дисперсии ε в спиртовых растворах при исследовании их более известным м рассмотрим известное соотношение для величины tgδ проводящей жидкости: tgδ= tgδ0 + 2χ / νε. Первое слагаемое в этом соотношении обусловлено ориентационными потерями, второе — токами проводимости. На частотах, менее 1МГц, в C-способе, как известно, преобладает вклад от второго слагаемого. В результате понижение частоты измерения ν сопровождается увеличением tgδ и снижением добротности контура с находящимся в измерительном конденсаторе раствором. Для исследуемых спиртовых растворов нижним пределом применимости C-способа является частота ~1 МГц, на которой, как видно на рис. 3, различия между значениями ε спирта и его растворов почти исчезают. В результате C-способом низкочастотная дисперсия ε не фиксируется.

Не исключено, что возникающие внутри жидкости токи проводимости при измерении ее диэлектрических свойств C-методом не только затрудняют регистрацию низкочастотной дисперсии, но и настолько искажают сольватные оболочки ионов, что приводят к исчезновению дисперсии ε , связанной с их релаксацией. В то же время значения ε L находятся в столь слабых электрических полях (см. условие (13)), что сила, с которой поле действует на заряд, оказывается меньше силы вязкого трения. В результате токи проводимости в жидкости не возбуждаются, сольватные оболочки ионов не искажаются, появляется возможность их исследования. Таким образом, достоинством индуктивного метода является то, что он фактически является методом неразрушающего контроля состояния растворов.