Influence of magnetic field on the dielectric characteristics in manganese sulfide substituted with thulium

In spacecraft, electronics operate in extreme conditions, where temperature changes occur in the range of hundreds of degrees. It is necessary to find materials, for example, based on multiferroics, which can show stability in these circumstances.

Materials in which the relationship between magnetic and electrical properties [1–4], magnetoelectrics and multiferroics [5–8] is manifested, are of interest from both fundamental and applied points of view. Particular attention is drawn to materials that exhibit magnetoelectric properties at room and higher temperatures in connection with their practical application in microelectronics for recording and storing information. Bismuth ferrite BiFeO 3 [9–11] belongs to such studied materials. The effect of giant magnetocapacitance was observed in LuFe 2 O 4 [12] at room temperature and is explained by charge fluctuations with different spins in Fe²⁺ and Fe³⁺ ions as a result of removal of degeneracy between two types of charge order by an external magnetic field.

The magnetocapacitance in an electrically inhomogeneous medium can be due to the Maxwell – Wagner effect [13] as a result of the tensor nature of the interaction of current carriers with magnetic and electric fields and mixing of the longitudinal and transverse components of conductivity. In the model, the magnetocapacitance is positive provided that the size of the electrical inhomogeneity is an order of magnitude greater than the mean free path of an electron, the measurement time 1/ω exceeds the scattering time, and the matrix is dielectric [14].

How the magnetocapacitance changes in electrically inhomogeneous semiconductors with compensation for the charge of regions with chemical phase separation remains unclear. In this case, it is necessary to take into account the mobility of electrons and holes, the Coulomb interaction, and the recombination of charges. In Tm х Mn 1-x S solid solutions above room temperature, a magnetoimpedance was found, in particular, an increase in reactance in a magnetic field. This effect may be due to a change in the capacitance and inductance of the sample under the action of a magnetic field [15; 16].

The purpose of the study is to establish the type of electric polarization, the mechanism of relaxation, the effect of the magnetic field on the dielectric characteristics and dielectric losses during elec- tronic doping of semiconductors depending on the size of the electrical inhomogeneity, which is determined by the substitution concentration of aliovalent ions.

Results and discussion

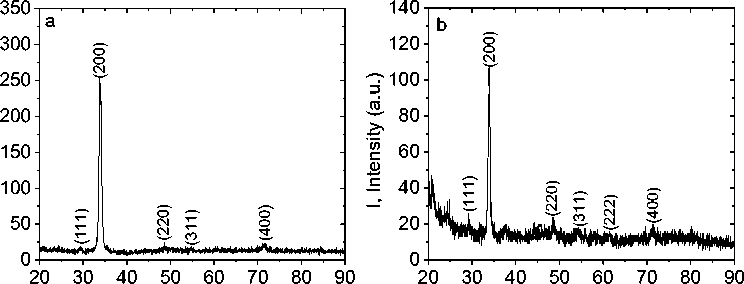
Solid solutions Tm х Mn 1-x S (0 < x < 0.15) were prepared by melting the initial polycrystalline manganese sulfides and thulium sulfides [16]. X-ray diffraction analysis performed on DRON-3 established a cubic lattice of the NaCl type. Fig. 1 shows the diffraction pattern of the Tm х Mn 1-x S solid solution. As the concentration of substitution of manganese by thulium ions increases, the intensity of the peaks decreases, which is associated with incoherent scattering.

2 Θ, degree                                   2 Θ, degree

Fig. 1. X-ray diffraction patterns of the Tm x Mn 1-x S solid solutions for concentrations x = 0.05 ( a ), x = 0.1 ( b ).

Рис. 1. Рентгенограммы твердых растворов Tm x Mn 1-x S для концентраций x = 0,05 ( a ), x = 0,1 ( b )

Dielectric permittivity and dielectric losses were determined from measurements of capacitance and loss tangent measured on an AM-3028 device, a component analyzer in the frequency range of 102–106 Hz at temperatures of 300–500 K. The magnetocapacitance of the sample was determined as

C ( H ) - C (0) Δε =              ,

C (0)

where С ( Н ) – is the capacitance of the sample measured in a magnetic field H = 12 kOe applied parallel to the capacitor plates; С (0) – is capacitance without magnetic field. To exclude leakage currents, mica, several micrometers thick, was placed between the sample and the capacitor plates.

From the frequency dependence of the permittivity, one can estimate the relaxation time and relaxation mechanism of dipole moments [17–19]. Exclusion of the leakage current will make it possible to estimate the contribution of the migratory polarization due to charges in the region with chemical phase separation and the size of this region when approaching the point of thulium ion flow through the lattice.

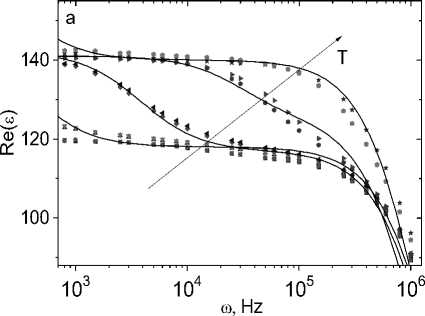
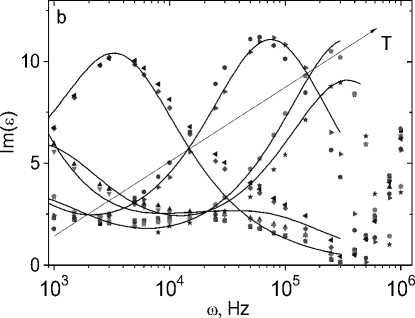
Figure 2 shows the frequency dependences of the real and imaginary parts of the permittivity on temperature. The frequency dependence ε(ω) can be divided into two frequency ranges: low-frequency ω < ω c and high-frequency ω > ω c . In the low-frequency region, ε(ω) is described by the Debye relation with a maximum dielectric loss:

Re( ε ) = ε ₀ +

χ ₀ 1 + ( ωτ _c )²

Im( ε ) =

χ ₀ ωτ _c 1 + ( ωτ _c )²

where ε0 is the high-frequency contribution to the permeability; χ 0 is the static susceptibility of the dipoles. The maximum Im(ε(ω)) shifts towards higher frequencies upon heating, and the relaxation time found from the relation ωτ c = 1 is described by the Arrhenius function τ = τ0exp(ΔE/kT), where ΔE is the activation energy, ΔE = 0.55 eV. At high frequencies ω > ω c , the complex permittivity depends linearly on frequency.

• ■1

• •2

• •3

• •4

• •5

• -6

►7

• •8

*9

• •10

Fig. 2. The real Re( ε ) ( a ) and imaginary Im( ε ) ( b ) parts of the permittivity of the sample Tm 0.05 Mn 0.95 S without field H = 0 kOe at temperatures T = 300 (1), 350 (3), 400 (5), 450 (7), 500 (9) K and in magnetic field H = 8 kOe at temperatures T = 300 (2), 350 (4), 400 (6), 450 (8), 500 (10) K on the frequency ω. The permittivity in the Debye model (solid line) ( a , b )

Рис. 2. Действительная Re( ε ) ( a ) и мнимая Im( ε ) ( b ) компоненты диэлектрической проницаемости образца Tm 0.05 Mn 0.95 S без поля H = 0 кЭ при температурах T = 300 (1), 350 (3), 400 (5), 450 (7), 500 (9) К и в магнитном поле H = 8 кЭ при температурах T = 300 (2), 350 (4), 400 (6), 450 (8), 500 (10) К на частоте ω. Диэлектрическая проницаемость в модели Дебая (сплошная линия) ( a , b )

Dielectric losses are caused by electron-phonon interaction. The imaginary part of the permittivity is related to the real part of the optical conductivity σ by the relation Im(ε) = σ/ω. In disordered semiconductors with a hopping type of conduction, a resonant and relaxation mechanism of conduction can be realized. If the energy of the Coulomb repulsion of electrons located at a distance R is less than the thermal energy e ²/ε R << kT, then the relaxation optical conductivity prevails [20]:

σ ( ω ) = ¹ π ² e ² ag ² h ω ² R ⁴ ,                                 (4)

where а is the electron localization radius; g is the electron density of states at the Fermi level. In this case, Im(ε) = Аω. The crossover frequency ω с from Debye relaxation to relaxation conduction associated with the absorption and emission of phonons is determined by the electron localization radius and the electron density of states g . If we assume that the electron is localized in the region of chemical phase separation created by thulium ions, and the localization radius does not depend on temperature, then an increase in ω с above 400 K is associated with an increase in the electron density of states at the chemical potential level g ~ T².

In a magnetic field, the Debye relaxation time increases, the inflection point Re (ε) and the maximum Im(ε) shift towards low frequencies. As a result, the permittivity decreases in a magnetic field at ωτ = 1 by 0.5, 2.4, and 3.3% at T = 400, 450, and 500 K. More significant changes were found in the dielectric loss tangent, which depends on active losses, as a result of an increase in the scattering of electrons by local deformations and phonons in the region where thulium ions are located. Dielectric losses increase by 14 and 36% at T = 450 and 500 K and decrease to 15% at low frequencies at T = 350 and 400 K.

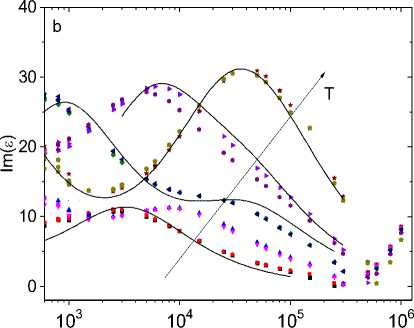
As the concentration increases, the radius of localization of electrons associated with thulium ions increases. Figure 3 shows the components of the permittivity of the Tm x Mn 1–x S sample versus frequency for a concentration x = 0.1. In these samples, the Debye and electron-phonon mechanism of relaxation of the induced electric polarization is also implemented [21]. Upon heating, the maximum of Im( ε ) shifts to the region of high frequencies. Activation energy ΔE = 0.2 eV (1550 cm^–1) is two times less than for x = 0.05. The crossover frequency found from the Im(ε(ω)) minimum increases as the sample is heated according to the power law ω с ~ Т^3/2.

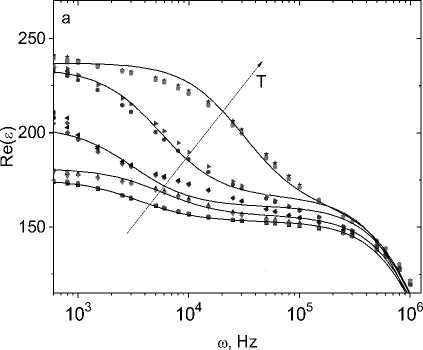
Fig. 3. The real Re( ε ) ( a ) and imaginary Im( ε ) ( b ) parts of the permittivity of the sample Tm 0.1 Mn 0.9 S without field H = 0 kOe at temperatures T = 300 (1), 350 (3), 400 (5), 450 (7), 500 (9) K and in a magnetic field H = 8 kOe at temperatures T = 300 (2), 350 (4), 400 (6), 450 (8), 500 (10) K on the frequency ω.

The permittivity in the Debye model (solid line) ( a , b )

ω , Hz

Рис. 3. Действительная Re( ε ) ( a ) и мнимая Im( ε ) ( b ) компоненты диэлектрической проницаемости образца Tm 0.1 Mn 0.9 S без поля H = 0 кЭ при температурах T = 300 (1), 350 (3), 400 (5), 450 (7), 500 (9) К и в магнитном поле Н = 8 кЭ при температурах Т = 300 (2), 350 (4), 400 (6), 450 (8), 500 (10) К на частоте ω . Диэлектрическая проницаемость в модели Дебая (сплошная линия) ( a , b )

Perhaps this is due to a shift in the chemical potential with respect to temperature and an increase in electron density g ~ T^3/4. In a magnetic field, the permittivity decreases and the maximum change Δε = 2.5% is reached at T = 450 K. At other temperatures, the magnetocapacitance does not exceed 0.5%. The shift of the maximum of the imaginary component of the permittivity to low frequencies in a magnetic field leads to a change in the sign of dielectric losses from positive to negative from δ(Im(ε)) = 0.024 to –0.08 at T = 450 K.

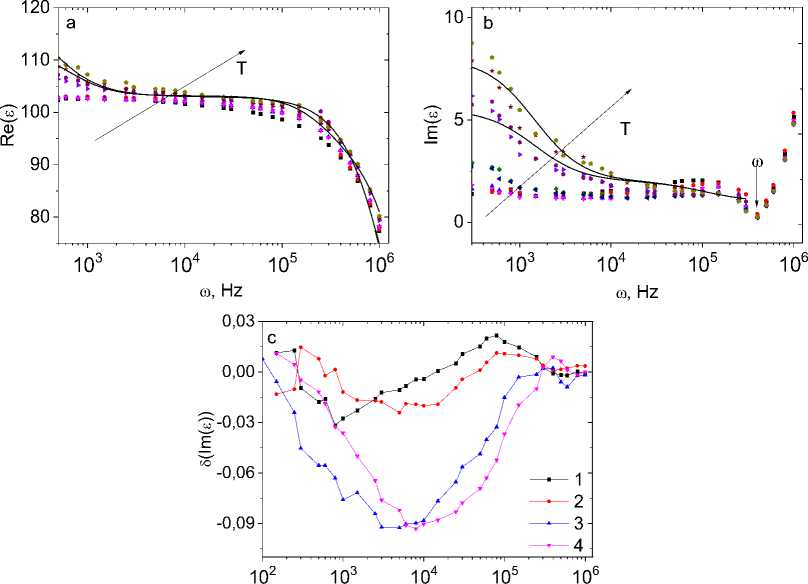
As the concentration of thulium ion percolation on the FCC lattice x c = 0.17 [22] approaches, the frequency dependence ε(ω) changes qualitatively (Fig. 4). In the frequency range 10²–10⁶ Hz, the permittivity is not described in the Debye model. The flow of Tm-Tm exchange bonds through the lattice leads to shunting of the capacitor plates and the absence of migratory polarization at the Mn-Tm ion interface. An increase in ε(ω) below 100 Hz is caused by the accumulation of charges near the capacitor plates. The imaginary component of the permittivity decreases in a magnetic field to 9% at Т = 450 and 500 K as a result of a decrease in conductivity σ(Н, ω) < σ(0, ω) (Fig. 4, c ).

The frequency at which the permittivity is due to relaxation conduction from phonons does not depend on temperature. This is due to the preservation of the electron density of states at the level of the chemical potential upon heating. For the concentration x = 0.15, there is no magnetic capacitance (∆ε < 0.005). The decrease in dielectric losses in a magnetic field is caused by a decrease in conductivity.

ω , Hz

Fig. 4. The real Re( ε ) ( a ) and imaginary Im( ε ) ( b ) parts of the permittivity of the sample Tm 0.15 Mn 0.85 S without field H = 0 kOe at temperatures T = 300 K(1), 350 K(3), 400 K(5), 450 K(7), 500 K(9) and in magnetic field H = 8 kOe at temperatures T = 300 K(2), 350 K(4), 400 K(6), 450 K(8), 500 K(10) on the frequency ω.

The permittivity in the Debye model (solid line) ( a , b ). The relative change of the imaginary part of the permittivity δ(Im(ε)) in magnetic field H = 8 kOe at temperatures T=350K(1), 400K(2), 450K(3), 500K (4) versus frequency ω ( с )

Рис. 4. Действительная Re( ε ) ( a ) и мнимая Im( ε ) ( b ) компоненты диэлектрической проницаемости образца Tm 0.15 Mn 0.85 S без поля H = 0 кЭ при температурах T = 300 (1) , 350 (3), 400 (5), 450 (7), 500 (9) К и в магнитном поле Н = 8 кЭ при температурах Т = 300 (2), 350 (4), 400 (6), 450 (8), 500 (10) К на частоте ω. Диэлектрическая проницаемость в модели Дебая (сплошная линия) ( a , b ). Относительное изменение мнимой части диэлектрической проницаемости δ (Im( ε )) в магнитном поле H = 8 кЭ при температурах T = 350 (1), 400 (2), 450 (3), 500 (4) K в зависимости от частоты ω ( с )

Conclusion

The permittivity in the frequency range up to one megahertz with electron doping in Tm x Mn 1–x S is due to the migratory polarization of localized electrons and relaxation conductivity. In the Debye model, the relaxation time of the electric polarization is found, which has an activation character and is described by the Arrhenius law. In the vicinity of the concentration of the flow of thulium ions through the lattice, the contribution of the migratory polarization disappears, and the dielectric characteristics are due to relaxation conduction in the high-frequency range, the interval of which does not depend on temperature. In a magnetic field, the dielectric permittivity decreases by several percent and practically does not change in a sample with a concentration close to the percolation concentration. An increase in the relaxation time in a magnetic field leads to a shift in the maximum of dielectric losses to the low-frequency region and a change in the sign of dielectric losses in a magnetic field in frequency. A high inductance of the sample in a magnetic field is found.