Информационная модель поддержки процессов управления производственными потоками автоматизированного производства

Производственные структуры древовидного типа, к которым относятся автоматизированные системы управления производством, требуют иерархического управления, так как оно в наибольшей мере соответствует организационной структуре объекта и демонстрирует как трансформируется система управления применительно к рассматриваемым объектам. Тогда на выходе такого производства формируется конечный продукт как состав потока полных комплектов (ПК). Информационная поддержка данных процессов управления включает операции комплектования изделия, узлов, подузлов и так далее, вплоть до подузлов заданного уровня, при заданных нормативных уровнях числа комплектов с учетом длительности сборочных циклов и уровней комплектных запасов.

Описанная схема реализует многоуровневое (многоуровневое, согласно [1]) управление с оператором высшего уровня иерархии. Необходимо также учесть, что производственных мощностей для целей управления должно быть тем больше, чем выше порядковый номер органа управления, т. е. чем далее от конечной операции находится наш объект в древовидной производственной структуре.

Отметим, что действующие методики и нормативы [2, 3] не предусматривают резервирования производственных мощностей на цели управления, что противоречит задачам системы и обуславливает актуальность данной статьи.

Анализ исследуемой системы

Настоящая работа посвящена процессам управления в классе производств, функционирование которых характеризуется свойствами потока комплектов (ПК). Таковы сборочные, а также многие другие типы производств, в которых поток готовой продукции образуется путем «смешения» в определенной пропорции продуктов, поступающих по многим питающим потокам [4, 5].

Каждый из потоков % i (t) выдается производственным объектом 0 j , управляемым «собственной» системой регулирования Vi , на вход которой поступает сигнал рассогласования:

q_t(t) = X ? (t) - Q i - X i (t),                                                                    (1)

где X p (t) - программа выпуска продукции, задаваемая объекту 6 i ;

X i (t) - суммарный (накопленным итогом) выпуск продукции объектом 6 i , полученный интегрированием в блоке Z потока X i (t);

Q i - параметр, связанный с нормативным запасов, i -го продукта.

При надлежащем выборе единиц измерения продуктов, поступающих по питающим потокам, без нарушения общности можно положить, что в комплект входит по единице каждого из п продуктов.

Тогда ПК в каждый момент времени будет определяться самым «отсталым» из потоков:

%(t) = ^X(t),                                                                          (2)

X(t) = min1

Одной из основных задач настоящей работы является обоснование эффективности двух- и многоуровневого управления в исследуемых производственных системах, в то время как существующая практика ориентирована на использование лишь одноуровневого независимого управления каждым потоком [6, 7].

Двухуровневое управление (рис. 1) обеспечивается сочетанием операторов V i нижнего с оператором V верхнего уровня.

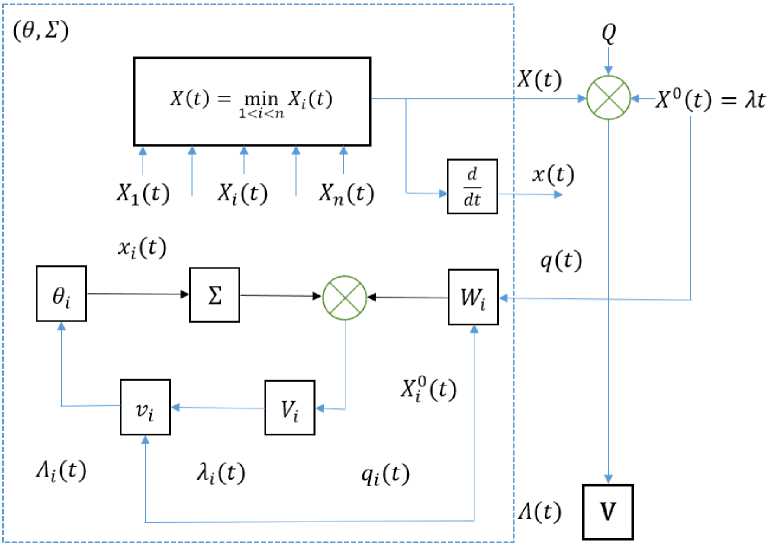
Рис. 1. Модель двухуровневого управления процессом формирования потока комплектов из заданных питающих потоков

Fig. 1. Model of two-level process control of forming of a flow of sets from the set feeding flows

Двухуровневая модель управления питающими потоками ПК

Вмешательство оператора V в работу объектов 0 ; осуществляется с помощью вспомогательных операторов V ; и W ; , влияя на формирование программ X⁰ (t) и корректируя в интересах системы решения A ; (t) операторов V ; , исходящих в своей работе из «эгоистических» интересов подведомственных им производств [8].

Оператор V вырабатывает координирующие решения путем преобразования сигнала рассо- гласования:

Q;(t)= Xf(t) + Q — X;(t),                                                              (3)

где X0 (t) = At - заданная системе программа выпуска комплектов, принимаемая далее линейной функцией времени;

Q - параметр, задающий нормативный уровень комплектных запасов в системе.

В современной практике управления [9] рассматриваемые производственные системы соот- ветствуют одноуровневому независимому управлению каждым из потоков:

Г Л^ (t) = A;(t) (x0(t) = x0(t),

которые отражают невмешательство оператора V в функционирование системы.

X ; (t) соответствуют операторы V ; и W ; , обеспечивающие соотношения.

Согласно работе [6, 10], в такого рода системах процесс (поток) %(t) относится к классу управляемых, т. е. дисперсия сигнала рассогласования q(t) будет ограниченной даже при liny,,„ D(n) < да,                                                                               (5)

что вытекает из сформулированных выше утверждений Е и F.

Таким образом, начиная с некоторой сложности системы, определяемой величиной п^, числа питающих потоков в ней, двухуровневая система управления (оператор V на верхнем уровне и операторы V ; - на нижнем) способна обеспечить более высокую упорядоченность ПК, нежели одноуровневое независимое управление каждым питающим потоком (рис. 2).

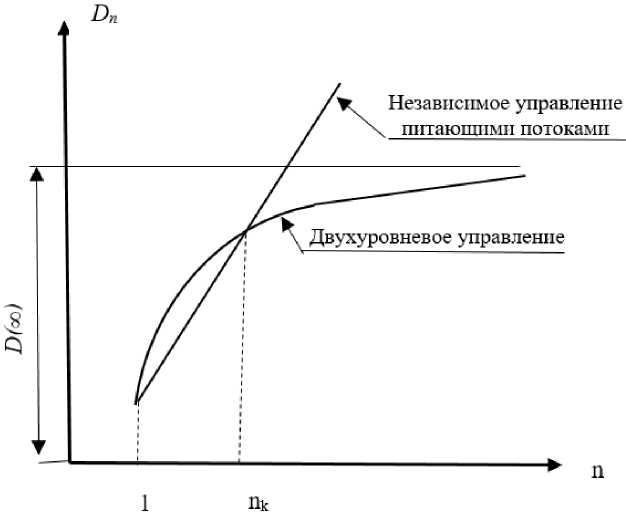
Рис. 2. Сравнительные графики оценки упорядоченности одноуровневого и двухуровневого управления питающими потоками Fig. 2. Comparative diagrams of assessment of orderliness of single-level and two-level management of the feeding flows

Многие реальные производственные системы, моделируемые рис. 1, состоят из сотен и даже многих тысяч питающих потоков [7, 11].

Существующая практика управления такого рода системами основана на принципе незави- симого управления каждым потоком, т. е. на выполнении условий (4). Девиз такого управления: «Система будет работать ритмично, если все питающие потоки ритмичны».

Будучи в принципе правильным, этот девиз толкает на максимальное «выжимание» ритмичной работы каждого питающего потока [8, 12].

Однако если таких потоков много, то даже небольшая неупорядоченность каждого из них приводит к хаотическому поведению ПК, вынуждая поддерживать высокие уровни управления, и работа должна быть построена таким образом, чтобы обеспечить ритмичный выпуск продукции при неритмичных шатающих потоках.

Эффективность такого подхода иллюстрирует один из возможных подходов к координации деятельности объектов 0;, состоит в выработке оператором V сигнала A;, задающего интенсив ность ПК; операторы V; и W; соответствуют равенствам:

f

A ; (t) = ^(t);

_ A(t)

dx°(t) _ A(t) dx°(t) dt Л dt комплектных запасов в качестве средства, сглаживающего выпуск готовой продукции.

Предложенный выше переход к двухуровневому управлению системой потоков реализует подход, свидетельствующий о пренебрежении индивидуальными особенностями объектов 0; и регуляторов V;. Учет таких особенностей потребовал провести сбор больших объемов статистической информации, соответствующей ее обработке и воплощению полученных результатов в алгоритмах V; и W;.

Если все объекты 0 ; характеризуются тем, что величина A ; (t) пропорциональна интенсивности всех внутренних процессов объекта, формирующих поток % ; (t), а операторы V ; безынерционны, то вмешательство в функционирование i -го замкнутого контура может быть интерпретировано как управление «ходом времени» в нем [2, 6, 13].

Действительно, при сделанных выше допущениях относительно свойств 0;, V;, V; и W; мы можем представить, что все контуры в замкнутых системах функционируют взаимозависимо, руководствуясь часами, отсчитывающими время τ, а оператор Λ вмешивается в скорость хода этих часов таким образом, что dT(t) _ A(t) dt = "Т".

За интервал натурного времени длительностью t процессы в объектах 0 ; и в целом в замкнутых системах, генерирующих питающие потоки, «проживут» T(t) часов. Указанным способом можно интерпретировать, например, управление продолжительностью рабочего дня (введение сверхурочных работ), либо управление скоростью движения сборочного конвейера [12, 14].

Совершенно естественным будет допущение, что процесс T(t) удовлетворяет условиям:

г        1 г? dT(t)                  t(7)-t(-7)

lim r^ да 57 " L_r — • ^{dt _} lim⁷ ^ “ —57— ^{_ 1}

0 < A(t) _ A • ^ < A* > A, первое из которых свидетельствует о том, что ресурсы, находящиеся в распоряжении оператора V, используются только для корректировки поведения ПК, а не для компенсации недостатка ресурсов, подведомственных операторам V;; второе условие (9) свидетельствует об ограниченности ресурсов, находящихся в централизованном подчинении оператора V.

Очевидно, что для выполнения условий (8) и (9) необходимо, чтобы

0< A ; (t)< A * _ A^ A > A, (10) т. е. операторы V ; должны располагать собственными резервами производственной мощности, обеспечивающими возможность выполнения программы X⁰(t) .

Отметим также, что условиям (4) независимого функционирования питающих потоков соот- ветствует равенство

T(t) _ t, — да

В связи с этим далее исследуется общий случай двухуровневой координации, из которого найдем частный случай независимого управления каждым из и питающих потоков, полагая справедливым условие (11). В рассматриваемом общем случае вместо условий (1) и (2) запишем (с учетом (10)):

Г^(т(О) = X0(r(t) + Qt - X^t));

I q(t) = X0(t) + Q- X(T(t)).

Введем также специальное обозначение для рассогласования q(t) при отсутствии координа- ции, т. е. при условии

q(t) = q(t)T(t)=t = X0(t) + Q - X(t)(13)

с учетом формул (13) и (3) получим

q(t) = q(T(t)) +A- [t-T(t) ].(14)

Показав эффективность двухуровневого управления, мы должны установить: не потребует ли такое управление дополнительных ресурсов – запасов и производственных мощностей в качестве «платы» за упорядоченность ПК.

Проанализируем это на примере координации, использующей управление «ходом времени» в автономных контурах управления [9, 10].

Использование ресурсов

Исследуем уровень некомплектного запаса t-гo продукта, определяемый соотношением

Zi,n(T(t)) = X^Tp)) - X(T⁽t)) = c?(x⁽t⁾) - q_z (T⁽t)) + Qi - Q.                         (15)

Характеристики системы определяются средними по времени уровнями запасов. Рассмотрим результаты усреднения по времени отдельных слагаемых выражения (15).

Введем для операции усреднения по времени некоторой функции ф(t) обозначение

Jr*$(t)dt = limT ,да ;^^ J’[T^(t)dt, с учетом которого, а также равенства (16) имеем

A² • J* ^[T(t) - t^] • d^[T(t) - t^] = limT >да:^t • | • [c?(x(t)) - q(t)]² |

t = T 0 t = -T

.

Последний предел равен нулю по вероятности в силу ограниченности дисперсий сигналов ц(М)) и q(t).

Теперь рассмотрим результат усреднения процесса q (^(t)) с учетом соотношений (15), (17) и (10):

J* q(t(C)) d⁽t) = J* q(T⁽t)) Mt) - J* q⁽t) • [^ - 1] • dt=

= q⁽«) - J* q⁽t) • [^ - 1 dt].

Второе слагаемое в этом выражении есть коэффициент корреляции процессов q(t) и A(t), детерминистская связь между которыми определяется оператором V.

Для последнего естественно предположить выполнение условий:

A(t) Л

-

1=I1

> 0, q(t) > q 0,q(t) = q*

< 0, q(t) < q"

*

,

*

где <, =, > – параметр системы управления.

Условия, подобные (19), всегда выполняются алгоритмами регулирования, используемыми в практике управления производством [10, 15].

Из условий (18) и равенства (19) следует

J* q(T⁽t)) d⁽t)< q⁽n) = J* q⁽t) dt,

причем равенство имеет место при условии (13), когда согласно равенству (9) A(t) = A, — да < t < + да.

Отметим, что левая и правая части неравенства (21) отличаются друг от друга на конечную величину

J*q(tMA^;)-ipdt

коэффициента корреляции, в то время как правая часть неограниченно возрастает с ростом числа n питающих потоков.

Перейдем теперь к усреднению второго слагаемого в формуле (16):

J* q⁽T(t))dt = J* q_t⁽T(t)) • A^ • di(t).

Примем при этом во внимание статистическую независимость процессов q(x) и q(x) при и ^ да, откуда вытекает асимптотическая взаимозависимость обоих сомножителей под знаком интеграла в равенстве (23), так что при достаточно большом числе и питающих потоков

J* qt⁽T(t)) dt = J* q;⁽t)dt = q_t                                                              (24)

из питающих потоков. При этом разность правой и левой частей неравенства есть величина конечная и относительно малая.

Рассмотрим поведение уровня комплектного запаса, который в соответствии с формулами (16) и (17) равен

z(t) = X(x(t)) - X⁰ (t) = Q - q(t) = Q - q(T(t)) - A • [t - T(t)],                      (25)

и отметим, что поддержание комплектного запаса обеспечивает ритмичность выдачи продукции сборочными производствами, для которых величина

P(z(t)< 0) < p                                                                    (26)

есть вероятность «срыва» производственной программы, характеризующая качество функционирования системы, ограниченное заданным значением p.

Очевидно, что организация двухуровневой координации может рассматриваться в качестве одного из способов выполнения условия (26) путем стабилизации комплектного запаса на среднем уровне

z(p,n) = J* z(t) • dt = Q - J* q(t)dt < да,                                             (27)

определяемом путем надлежащего выбора параметра

Q = Q(p,и).

Сопоставление полученных выше соотношений (22) и (24) с выражением (17) приводит к справедливому при большом и соотношению

J* ^zqn (^T(t)) • ^dt< J* ^zqn^(t) = ^                                                    ⁽²⁸⁾

утверждающему, что в условиях двухуровневой координации средний уровень некомплектных запасов не превысит уровня, образующегося в условиях независимого управления каждым limy >да г(р,и) = z^ = да в силу ограниченности дисперсии сигнала q(t) согласно условию (9).

Переходя к условию (15), определяющему одноуровневое независимое управление каждым питающим потоком, имеем из формул (26), (17)

г(р,и) = Q - J* q(t)dt = Q - q(n), откуда с учетом равенств (7) и (8) следует lim^ ,да г(р,и)=да.                                                                           (29)

Отсюда, сравнивая выражения (28) и (29) и учитывая при этом равенство (25), сделаем вывод: основной эффект при переходе к двухуровневому управлению достигается за счет сокращения уровня комплектных запасов в системе, что иллюстрируется рис. 1.

Очевидно, что при n > n_k,i суммарный запас в условиях двухуровневой координации будет ниже запаса при одноуровневом независимом управлении каждым из питающих потоков [2, 11, 14]. Однако это потребовало введения в эксплуатацию дополнительной производственной мощности, подведомственной оператору У верхнего уровня.

Величина введенных дополнительно ресурсов мощности для объекта составит согласно равенствам (5) и (13)

[^Лг ^-11 •^л*.

Снижения суммарного запаса в системе можно достичь, также и не привлекая извне дополнительных ресурсов, но централизуя распоряжение частью мощности, имеющейся у объектов Qj.

Снижение производственной мощности, подведомственной операторам У;, приведет к тому, что поведение запасов будет соответствовать пунктирным кривым на рис. 1, так что двухуровневое управление будет эффективным при n > nk,i* > nk,i.

Таким образом, с ростом сложности производственной системы (см. рис. 1) переход к двухуровневому, а затем и к многоуровневому управлению обеспечивает более эффективное использование ресурсов (мощностей и запасов) в целях упорядочения процесса выпуска готовой продукции.

Заключение

Рассматривая построение многоуровневой системы, можно обратить внимание на то, что, стремясь к достижению целей системы (см. рис. 1), мы не учитывали цели отдельных ее элементов, т. е. в нашем случае - операторов Vj..

Судить о том, насколько гармонируют решения, принимаемые оператором V, реализующим цели системы, и решения, принимаемые операторами Vj, стремящимися к достижению собственных целей, можно, воспользовавшись в качестве меры этой гармонии какой-либо статистической характеристикой связи между процессами. Например, в роли такой меры может выступить коэффициент корреляции этих процессов.

Система кривых, обозначенных жирными линиями, иллюстрирует поведение запаса i-ro продукта с ростом числа питающих потоков. Очевидно, что при n > n_k,i суммарный запас в условиях двухуровневой координации будет ниже запаса при одноуровневом независимом управлении каждым из питающих потоков.

Однако это потребовало введения в эксплуатацию дополнительной производственной мощности, подведомственной оператору V верхнего уровня. Величина введенных дополнительно ресурсов мощности для объекта составит согласно равенствам (5) и (13)

• [Т-1Р ЛГ

Снижения суммарного запаса в системе можно достичь, также и не привлекая извне дополнительных ресурсов, но централизуя распоряжение частью мощности, имеющейся у объектов Qj.

Снижение производственной мощности, подведомственной операторам Vj, приведет к тому, что поведение запасов будет соответствовать пунктирным кривым на рис. 1, так что двухуровневое управление будет эффективным. Очевидно, что максимум достигается при п = 1, когда Л(£) и Aj(t) связаны между собой детерминированной зависимостью.

Изложенное может трактоваться следующим образом:

• во-первых, полная гармония интересов V и Vj достижима только при п = 1;

• во-вторых, можно говорить о полной дисгармонии интересов, но, несмотря на это, цели системы достигаются;

в-третьих, если при построении системы (см. рис. 1) мы, повышая эффективность использования ресурсов, хотим сохранить некоторый допустимый уровень гармонии интересов операторов верхнего и нижнего уровня, в результате естественно приходим к необходимости строить не двухуровневую, а многоуровневую систему управления, в которой число «нижестоящих» операторов, подчиняющихся одному «вышестоящему» оператору, достаточно мало, чтобы обеспечить требуемый уровень гармонии их интересов.

Многоуровневое управление наряду с другими задачами решает важнейшую проблему обеспечения определенного уровня гармонии целей системы как целого и ее элементов.