Информационная технология анализа качества системы обнаружения объектов на изображениях

Как правило, качество системы обнаружения объектов на изображениях определяется по критериям, имеющим смысл вероятностей: ошибок обнаружения объектов, неправильной классификации изображения, недостижения системой цели своего функционирования и т.п. [1,2]. В интересных для практики ситуациях значения подобных показателей качества довольно малы, в связи с чем их экспериментальное измерение весьма затруднительно. Дополнительные сложности вызывает и высокая размерность воздействия на входе системы обнаружения, имеющей дело с изображениями. Ниже излагается метод проведения статистических экспериментов с системой обнаружения объектов на изображениях, позволяющий существенно сократить число экспериментов, необходимое для получения требуемой точности оценивания се характеристик качества по сравнению с традиционно используемыми методами |3,4]. Отметим, что все изложенные результаты можно использовать и при оценке вероятностей редких событий, имеющих достаточно произвольный смысл.

• 2.    ОЦЕНИВАНИЕ ХАРАКТЕРИСТИК КАЧЕСТВА СИСТЕМЫ ОБНАРУЖЕНИЯ ОБЪЕКТОВ С ПОМОЩЬЮ СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Примем описание системы обнаружения в виде бинарной функции G(X) с аргументом X = (х(),х] .....Xj _J - L-компонентным вектором случайного воздействия на се входе. Эта функция принимает значение 0 или 1 при решении, соответственно, об отсутствии объекта во входном воздействии (гипотеза Н(|) или о его наличии (гипотеза Hf). Качество системы характеризуется вероятностями ложного обнаружения - а и пропуска объекта - р [2,4]:

а= jG(X)w(x/HjdX, R1

р= f(l-G(X))w(x/H,)dX,                                           (2)

R1

где W(X/HO) и W(X/HJ -плотности распределения вероятностей входного вектора в случае справедливости гипотез Н() и Hj соответственно. Вероятности (1) и (2) по сути отличаются друг от друга лишь ситуацией на входе системы G и трактовкой ее отклика, поэтому ниже для краткости ограничимся рассмотрением только одной из них, а именно, а.

Стандартным методом оценивания неизвестной вероятности а по результатам N независимых наблюдений над системой обнаружения объектов является метод прямого статистического моделирования [3,4,5,6], который заключается в вычислении оценки вида б-^°(х""), 1 п=0

где Х'^П1 - реализация вектора X с плотностью вероятностей w(x/H_(l) в п-ом эксперименте.

Оценка (3) является несмещенной, ее точность характеризуется шириной интервала [a-d,a + d], в который она попадает с заданной доверительной вероятностью у. Выражение для величины d имеет вид [3,4,5]:

ч = с,Ж                               №

где D_g - дисперсия отклика системы G, равная здесь

D_g = a(l - a);

С? - коэффициент, определяемый по заданной у с помощью функции Лапласа (обычно полагают С, =2 или Су =3, что при N » 1 соответствует доверительной вероятности у = 0.95 и у » 0.997). Из формул (4) и (5) следует выражение для относительной ошибки оценивания:

d 1 - а

8 = - = С a ? V aN

Из формулы (6) видно, что при оценивании малых значений вероятности а для получения высокой точности оценочная процедура (3) может потребовать очень большого числа экспериментов N с системой G. Улучшить точность оценки а при заданном N или, что эквивалентно, уменьшить число экспериментов при заданной точности позволяет применение методов понижения дисперсии при оценивании математического ожидания случайной величины. Одним из них является метод значимой выборки (МЗВ), который наиболее удобен в рассматриваемом случае [3,4,5,6].

Пусть все возможные входные векторы имеют плотности распределения вероятностей, различающиеся только значениями некоторого параметра ст (для случая оценивания вероятности а это позволяет сделать переобозначение. w(X/H₀) = W(X,ct)). Тогда суть МЗВ состоит в том, что входное воздействие с заданной плотностью W(X;ct) заменяется модифицированным, имеющим плотность w(X;CT_m), а затем отклик системы

G корректируется соответствующим весовым коэффициентом. Соотношение (1) можно переписать в другой форме:

a = Jg(X) W(X;a)dX = J G(X)

rl

rl

W(X;a)

W(X^,n \   ’ m

-W|X;am

) dX,

из которой следует, что при обработке N независимых наблюдений над системой наряду с оценкой (3) можно применять и оценку вида а =

1 N'* i^M п-0

w(x,n);o) wlxlnl;%)

где Х’п| - реализация вектора X с модифицированной плотностью в n-ом эксперименте. Точность оценки (7) характеризуется показателем, аналогичным показателю (4):

d -С

m С7у N ’ где Dz - дисперсия случайной величины

Z = G(X)

W(X;o)

W(X:«J

Сопоставляя (4) и (8), видим, что при заданном N для повышения точности оценки (7) по сравнению с оценкой (3) необходимо выполнение неравенства

D_zg-                                                          (9)

Это условие будет выполнено, если выбрать <тт так, чтобы весовые коэффициенты W(X;o)/w(X;om), используемые в оценке (7), были меньше единицы для тех X, при которых G(X)=1.

Если оценивать единственное значение а для конкретного распределения вектора X. то можно найти оптимальное с , минимизирующее дисперсию Dz, и, соответственно, показатель (8) [7]. Однако МЗВ открывает и более широкую возможность снижения вычислительной сложности моделирования, позволяя оценивать сразу несколько значений и даже целую зависимость а от варьируемого параметра распределения входного вектора на основе одних и тех же откликов системы G [8,9]. Действительно, если зафиксировать величину а , при которой проводится моделирование, то после введения обозначений к = —,                                                                (10)

С(Х.к) =

^W(X;ka„) ^w(x;°J

из (7) получим оценку сразу всей функции <х(к):

А(к) = ^^с(х1п|)с(х1п,,к).

п-0

Ценность МЗВ состоит также и в том, что при выборе модифицированной плотности распределения входного вектора не нужна информация о процессах преобразования, осуществляемых системой. Поэтому к системе G можно отнести все неизвестные и трудноформализусмыс факторы, в том числе и формирование сложной модели наблюдения сигнала, действие шума и нелинейных искажений, процедуру принятия решения человеком-оператором. Единственным условием применимости МЗВ является наличие доступа к реализациям вектора X для их использования при расчете весовых коэффициентов в формулах (7) и (12). При проведении моделирования с применением синтезированных тестовых входных сигналов это условие всегда может быть выполнено.

Далее будем полагать, что входное воздействие X соответствует случайному шуму наблюдения изображения, на котором может находиться подлежащий обнаружению объект, а параметр а имеет смысл СКО (среднеквадратическое отклонение) шума. В таком случае использование МЗВ при проведении экспериментов по обнаружению заключается в увеличении а до некоторого значения а_т, т.е. в переходе к "плохим" условиям наблюдения. Затем по формулам (11), (12) производится пересчет получаемых решений для "лучших" условий (для с< ст_т или, по (10), для к<1). В результате получается оценка зависимости искомой вероятности от уровня шума. "Базовое" значение СКО а , являющееся максимальным из рассматриваемых, следует здесь выбирать так, чтобы ему соответствовала настолько большая вероятность а(1), что ее можно было бы достаточно точно оценивать с помощью прямого статистического моделирования при малом N.

• 3.    МОДИФИКАЦИЯ МЕТОДА ЗНАЧИМОЙ ВЫБОРКИ ДЛЯ МНОГОМЕРНОГО ВХОДНОГО ВОЗДЕЙСТВИЯ

В реальных задачах обнаружения объектов на изображениях входное воздействие является существенно многомерным. При этом на решение, принимаемое системой обнаружения, могут не влиять (или слабо влиять) многие компоненты вектора X (назовем такие компоненты "фиктивными"). Рост размерности X и появление в нем фиктивных компонент быстро снижает эффективность описанной выше схемы МЗВ. Причина этого ухудшения заключается в появлении рассогласования между весовыми коэффициентами в формулах (7), (12) и откликами системы: из-за дополнительных фиктивных компонент при G(X)=1 весовые коэффициенты принимают значения как меньше, так и больше единицы, что в итоге приводит к нарушению условия (9).

Можно избежать негативных последствий такой ситуации, если произвести дополнительную рандомизацию входного воздействия путем его домножения на независимую неотрицательную случайную величину ^ с плотностью распределения вероятностей W.(^). Эта рандомизация позволяет свести многомерный случай к одномерному и использовать МЗВ в скалярном варианте, модифицируя плотность не вектора X , а величины § [8,9].

При поступлении произведения Х£ на вход системы вместо вероятности ложного обнаружения (1) имеем:

g= jjG(X§)w(x/H0)w^)dXd^. (13)

rl о

Положим, что CKO компонент вектора Х^ близко к от, т.е. реализуются плохие условия наблюдения, при которых вероятность (13) достаточно велика и удовлетворительно оценивается с помощью прямого статистического моделирования. Следуя схеме МЗВ, воспользуемся результатами этого же моделирования для оценивания меньших значений g, соответствующих лучшим условиям наблюдения. Для этого произведем модификацию входного воздействия, состоящую в умножении его СКО на положительный коэффициент к<1. Такая модификация эквивалентна умножению на к только величины ^ . При этом вероятность (13), зависящая от параметра к, будет равна

g(k)= j jG(Xk^)w(x/H0)w^)dXd^ = J jG(Xy)w(x/H0)|w^jdXdy, (14)

RL 0                                      RL О где у = Ц - новая переменная интегрирования. Из последнего выражения имеем два следствия. Во-первых, ему тождественна запись оо      — W —

G(Xy)-^TW(X/HoMy) dXdy’

rl о из которой следует, что в качестве оценки вероятности (14) можно использовать величину eW = KLG(x'"<)cM.                               (15)

п=0

где Х|п|, ^п - реализации случайного вектора X и случайной величины Е, в п-ом эксперименте, а

I w«(k)

Cfek)- w,({)

• -    весовой коэффициент при усреднении откликов системы G. Во-вторых, выражение (14) может быть переписано в виде

g(k) = |а(у)^/р^у,(17)

о где

а(у)= jG(Xy)w(x/H₀)dX r^l

• -    вероятность ложного обнаружения при модификации входного вектора X умножением на коэффициент у. Согласно п.2, значения функции а(у) при 0<у<1 являются искомыми величинами, которые требуется определить по наблюдениям за системой G. Для оценивания этой зависимости нужно решить интегральное уравнение (17), заменив его точную левую часть на оценку (15). В общем случае для приближенного решения интегрального уравнения можно использовать итерационные методы |10] с естественными для а(у) ограничениями на положительность и монотонное возрастание.

Однако, как будет показано ниже, существуют ситуации, когда можно обойтись без применения трудоемких итерационных процедур.

Для осуществления предлагаемой рандомизации входного воздействия и решения интегрального уравнения (17) необходимо выбрать конкретный вид плотности распределения вероятностей W^). При выборе этой плотности следует в первую очередь учитывать ее влияние на качество оценки (15): при единичных откликах системы G весовые коэффициенты (16) должны быть по возможности минимальными. Кроме того, желательно, чтобы выбранная плотность упрощала решение уравнения (17). Исходя из этих соображений, предлагается использовать для рандомизации случайную величину ^ с плотностью вида где а>0, Ь<0 - параметры распределения;

А- аЬ (Ь-а) - нормировочная константа.

Подставив (18) в уравнение (17), имеем:

g(k) = I,(k) + I2(k),< где

I,(k) = Ak'aJa(y)ya"'dy, I2(k) = Ak'bJa(y)yb'’dy. 0k

Для первых двух производных функции (19) имеем выражения:

g'(k) = -|l1(k)-|l2(k),(20)

, , а(а + 1) , . b(b + l) , , ab . .

8^к = —к5—11 к  —к5—^ к + к7"^

Формулы (19)-(21) могут рассматриваться как система трех линейных уравнений относительно I,(k), l2(k) и a(k). Из этой системы, в частности, находим:

a(k) = L(g(k)) = g(k) + ^-^^kg'(k) + ^k2g'(k).(22)

Выражение (22) представляет собой решение интегрального уравнения (17), записанное в явной форме.

После проведения статистического моделирования для получения оценки a(k) следует подставить в (22) значения оценок g(k), g'(k) и g'(k). Оценка g(k) здесь вычисляется по формуле (15) с весовыми коэффициентами, определяемыми из (16), (18):

к s k"b

п ри 0 < ^ < к, п ри к <£< 1, п ри £> 1.

Хорошие же оценки производных найти существенно труднее, поскольку весовые коэффициенты (23) и, следовательно, оценка g(k) не являются дифференцируемыми по к функциями (хотя истинная функция g(k) - гладкая). В связи с этим перед численным дифференцированием следует аппроксимировать оценку g(k) какой-либо достаточно гладкой функцией. Можно осуществить такое сглаживание с помощью кубических сплайнов, являющихся дважды непрерывно дифференцируемыми функциями в области своего определения [11]. Пусть gs(k) - результат сплайн-аппроксимации функции g(k), а g'(k) - оценка производной g'(k), полученная численным дифференцированием функции gs(k). Для получения более гладкой зависимости функции g'(k) от к ее также можно сгладить кубическим сплайном. Результат этого сглаживания обозначим g's(k). Действуя аналогичным образом, определяем оценку второй производной - g"(k) (дифференцированием g's(k)) и ее сглаженный вариант - g”(k). После этого получаем возможность вычислить и искомую оценку вероятности ложного обнаружения:

a(k) = L(gs(k)) = gs(k) + ^^^kg's(k) + ^k2g;(k). (24)

Указанные два метода нахождения оценки вероятности ложного обнаружения а(к) (из интегрального уравнения (17) и из уравнения (24)) являются весьма трудоемкими при реализации и требуют оптимизации большого количества параметров. Предпочтительнее в этом смысле подход, состоящий в следующем.

Если система обнаружения G является пороговой, а входные воздействия стандартными гауссовскими, то вероятность ложного обнаружения вычисляется аналитически:

ас(к) = 1-ф(с/к), где Ф(х) - функция Лапласа, с - порог. В этом случае в соответствии с (17) легко рассчитывается и зависимость gc(k). Считая данные зависимости типичными, для каждой реализации оценки g(k) и начального порогового значения cQ можно найти такое значение порога с, при котором gc(k) будет наиболее близка к g(k). В случае среднеквадратического приближения для этого необходимо:

• -    для некоторого множества k₁,...,k_r значений аргумента к определить величины Дк₁,...,Дк_г таким образом, чтобы

gc0(k + Aki) = g(ki)- * = 1.-.г;

- вычислить масштабирующий коэффициент s по формуле:

• -    положить значение порога с = c_Q/s.

• 4. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Обозначим Ag(k) = g(k) - gc(k) - погрешность приближения. Тогда из уравнения (22) будем иметь:

а(к) = L(g(k)) = L (gc(k)) + L(Ag(k)). (26)

Поскольку L(gc(k)) = ас(к), L(Ag(k)) = а(к) - ас(к) = Да(к), то можно считать, что первое слагаемое в (26) представляет собой "опорное" решение, а второе - поправку к нему. В этом и состоит смысл предлагаемого метода оценивания зависимости а (к).

Для того, чтобы найти L(Ag(k)), необходимо произвести сглаживание функции Ag(k) (Ag(k), как и g(k) дифференцируемой не является). Однако для этого можно не прибегать к кубической сплайн-аппроксимации. В силу малости значений Ag(k) достаточную точность оценивания обеспечивает просто линейное сглаживание.

Нетрудно видеть, что изложенный подход к оцениванию а(к) практически означает аппроксимацию системы обнаружения G неизвестной структуры пороговой системой с гауссовским воздействием на входе. Он не является таким общим, как два рассмотренных ранее, но для большинства систем обнаружения его использование вполне оправдано высокой вычислительной эффективностью и достигаемой точностью получаемых оценок.

Сначала продемонстрируем эффективность МЗВ на примере оценивания вероятности ложного обнаружения в случае скалярной аддитивной модели наблюдения "объект плюс шум". Предположим, что при отсутствии объекта все возможные воздействия X на входе системы G являются гауссовскими случайными величинами с нулевыми математическими ожиданиями и могут отличаться лишь значениями СКО ст. Подставив выражение для гауссовской плотности вероятностей в формулу (11), получим конкретизацию выражения для весовых коэффициентов:

С(Х,к) = ^ехр

к2 m

"Базовое" значение СКО ст , соответствующее синтезируемым входным воздействиям и используемое в формуле (27), для определенности положим равным единице. В экспериментах по оцениванию зависимости а (к) рассмотрим простейшую систему G, представляющую собой пороговое устройство:

G(X)-^

п ри п ри

Хйс, Хсс,

где значение порога с установим так, чтобы при тестовом входном воздействии вероятность ложного обнаружения была равна 0.2:

ст =1, с « 0.842, а(1) = 0.2.

Для сформулированных условий статистическое моделирование заключалось в следующем. По N=100 откликам системы осуществлялось вычисление оценок а (к) по формуле (12). Параллельно, с учетом (27) и (28), рассчитывались истинные вероятности а (к) для 0< к < 1. Для получения статистически устойчивых выводов было выполнено

М=50 серий экспериментов и вычислены:

• -    выборочная дисперсия оценки а(к):

М-1

Djk) = —     (к) " а2(к),                                                   (29)

м j-o где а.(к) - оценка а(к) в j-ой серии;

• -    размах ошибки оценивания, определенный с доверительной вероятностью у » 0.95 (экспериментальный аналог показателя (8) при С^ = 2):

dM(k) = 2VD^kh

• -    относительная погрешность оценивания:

dM(k)

МЮ-Дг                                 <31>

Чтобы сравнить МЗВ с методом прямого статистического моделирования, для последнего по формуле (6) при С^ = 2 вычислялись теоретические относительные погрешности оценки вероятностей а (к).

Результаты экспериментов и расчетов представлены на рис.1, 2. На рис.1 изображены также графики двух конкретных оценок d^k) и d2(k), полученных по 100 экспериментам. Анализ результатов позволяет сделать вывод о том, что оценка d(k), вычисленная по формулам (12), (25), при всех расчетных значениях к оказывается точнее

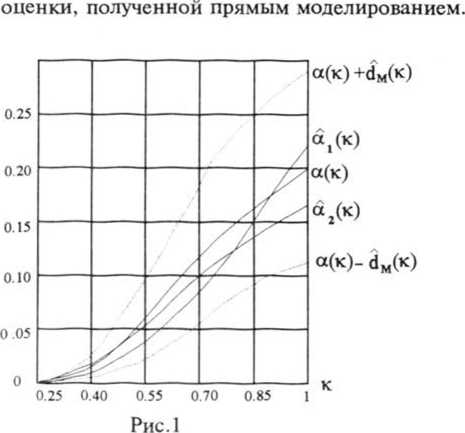
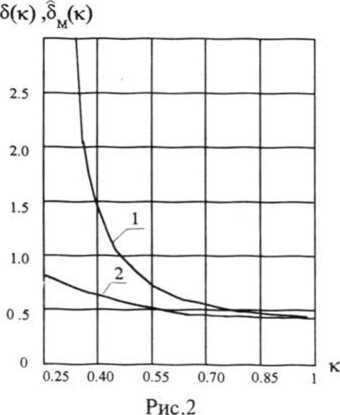
Результаты оценивания веро-                      Относительная погрешность ятности а (к) в скалярном                         оценки d(k) в скалярном случае при N=100.                                случае при N=100:

1 - прямое статистическое моделирование; 2 - МЗВ.

Этот выигрыш особенно велик при малых значениях оцениваемой вероятности. Заметим, что по результатам N=100 экспериментов над системой G оценивание вероятностей, меньших 0.01, с помощью прямого моделирования практически невозможно, в то время как МЗВ дает вполне удовлетворительный ответ.

Вместе с тем с увеличением размерности входного вектора точность МЗВ быстро снижается и становится значительно хуже, чем при прямом моделировании. Данное обстоятельство и стимулировало разработку модификаций МЗВ, эффективных в случаях многомерных входных воздействий.

Покажем, какие результаты оценивания вероятности а(к) дает описанный в п.З подход, основанный на аппроксимации системы обнаружения пороговой системой. Для использования этого подхода нужно решить следующие вспомогательные задачи: - выбрать значения параметров а и b плотности вероятностей (18) рандомизирующей случайной величины £ ;

• -    определить начальное значение порога c_Q;

• -    определить число и расположение значений аргумента к в интервале |0,1], используемых для расчета "опорного" решения ajk) с учетом значений оценки g(k).

Поиск наилучшего (по критерию точности оценки) решения этих задач требует проведения большого объема экспериментальных исследований. Ниже мы ограничимся подбором требуемых величин, обеспечивающих удовлетворительные результаты оценивания для рассматриваемого демонстрационного примера.

Пусть для обнаружения объекта на изображении применяется корреляционный алгоритм [1,2), действие которого заключается во взвешенном суммировании отсчетов функции яркости (компонент многомерного входного сигнала) и в сравнении суммы с порогом. Очевидно, рандомизация многомерного входного воздействия случайной величиной ^ эквивалентна рандомизации суммарного сигнала. Следовательно, в данном случае можно упростить вычислительные эксперименты с системой обнаружения, рассматривая ее в простейшей форме (28) со скалярным сигналом X на входе.

Для входного воздействия X, имеющего гауссовское распределение, моделирование процедуры оценивания зависимости a(k) по модифицированной схеме МЗВ с дополнительной рандомизацией состояло в следующем. Сигнал X умножался на случайную величину £ с распределением (18), параметры а и b которого предполагались связанными соотношением:

а+Ь+1 = 0.                                                           (32)

Условие (32) равносильно тому, что М^=1, и оно гарантирует равенство средних значений входного вектора до рандомизации и после нее: МХ^ = МХМ^ = MX. Подобное предположение является вполне оправданным. Кроме того, оно существенно упрощает нахождение оптимальных значений параметров а и b и, в частности, приводит к отсутствию в уравнении (22) второго слагаемого.

Далее произведение Х^ подавалось на вход системы (28), имеющей тот же порог обнаружения, что и выше. По результатам N=500 экспериментов с помощью формул (15) и (23) строилась зависимость g(k). Начальное значение порога cQ при построении "опорного" решения выбиралось из условия:

gc (О *g(0-

Затем производилась коррекция g (k), основанная на значениях оценки g(k) в трех со точках: к( = 0.25, к2 = 0.65, к3 = 1 (см. формулу (25)). Строилось "опорное" решение «с(к), а поправка к нему с учетом условия (32) и в предположении линейного сглаживания погрешности Ag(k) полагалась равной

Да(к) = L(Ag(k)) = Ag(k).

Окончательно искомая оценка а (к) вычислялась по формуле:

а(к) = а.(к) + Ag(k).

Всего было выполнено М=50 серий экспериментов. После этого были вычислены характеристики точности оценивания (29)-(31) и установлено, что наилучшие показатели этих характеристик соответствуют значениям парамегров а=0.875, Ь=-1.875. На рис. 3, 4 представлены полученные при этом результаты оценивания. 5(к),8м(к)
						а(к) +dM(K)	1
0.20						а(к)                   2.0 а(к)- dM(K)          L5
0.15 0.10									2
						1.0	1
0 .05 0						0.5						■ -^
0.25 0.40    0.55    0.70   0.85 Рис.З Диапазон оценок зависимости а (к) для модифицированного МЗВ (N=500).						0.25 0.40    0.55    0.70    0.85 Рис.4 Относительная погрешность оценки а(к): 1    - прямое статистическое моделирование (N=250); 2    - модифицированный МЗВ (N=500).							к

Анализ зависимостей на рис.4 показывает, что относительная погрешность оценивания здесь близка к той, которая получается для прямого статистического моделирования при N=250, т.е. модифицированный МЗВ проигрывает при оценке конкретного значения а. Однако этот проигрыш, обусловленный дополнительной рандомизацией, не зависит от размерности входного воздействия и может полностью компенсироваться возможностью оценивания всей функции а (к) на основе одного цикла моделирования системы обнаружения. Данное обстоятельство свидетельствует о целесообразности применения предложенной процедуры оценивания, базирующейся на модифицированном МЗВ, для проведения статистических экспериментов с системой обнаружения объектов на изображениях.

• 5.    ЗАКЛЮЧЕНИЕ

Для проведения статистических экспериментов по оцениванию малых вероятностей ошибок перспективен метод значимой выборки, позволяющий сократить необходимое число экспериментов с системой обнаружения. Однако стандартная схема МЗВ неработоспособна при многомерном сигнале на входе системы. Предложена и экспериментально исследована информационная технология проведения статистических экспериментов, основанная на схеме МЗВ, модифицированной для многомерного входного воздействия. Эффективность технологии обусловлена возможностью получения всей зависимости оцениваемой вероятности от варьируемого параметра распределения сигнала за один цикл моделирования.