Информационно-вычислительная система для работы доставки корреспонденции по всему миру

В ходе статьи будет рассмотрено математическое обеспечение для выбора логистических перевозчиков (ЛП) для доставки готовой продукции (ГП), построен алгоритм, который лег в основу информационновычислительной системы «Система поддержки принятия решений при управлении транспортировкой готовой продукции предприятия».

Приведем математическую модель рассматриваемой задачи выбора ЛП.

Введем следующие обозначения:

— р - количество логистических перевозок ГП;

— K - количество критериев оценки перевозчиков,

—  Zp — количественные или качественные значения по каждому критерию.

Для критериев, входящих в потребительскую оценку i -ого ЛП CEi(Zp,^, Zp0), где i = 1,...,P, введем обозначения для следующих множества:

—   Zp = (Z p ,^, Z p } - стоимость услуги - перевозки;

—   Zp = (Z2,..., Zp} - надежность соблюдения графика доставки груза;

• —   Zp = (Z 3 ,_, Z p } - врем оформления перевозки;

• —   Zp = (Z 4 ,_, Z p } - скорость доставки;

• —   Zp = (Z 5 ,_, Z p } - степень ответственности за груз;

• —   Zp = (Z 6 ,_, Z p } - отслеживание отправок;

• —   Zp = (Z 7 ,_, Z p } - частота отправок;

• —   Zp = (Z 8 ,_, Z p } - “рейтинг” предприятия;

• —   Zp = (Z 9 ,_, Z p } - готовность схем маршрутизации перевозок;

—   Zp⁰ = (Z p⁰ ,^, Z p⁰ } - “коммуникабельность” предприятия.

Требуется выбрать перевозчика с наибольшей потребительской оценкой (1):

CEi(Zl ,„,Zp° ^ max).

Для получения сформированного решения в задаче планирования ТП необходимо решить три подзадачи, применяя следующие алгоритмы: Ch_transport, OPT_Route, Ch_carrier.

Алгоритм Ch transport используется для подзадачи Выбора TP, а именно выбор способа транспортировки и вида транспорта в системе планирования ТП при перевозках реагентов.

Входными данными для алгоритма Chjransport являются N s = {N 1 ,…, N s } - способы транспортировки; V ^ = {V ^ ,..., V^_T } - значение показателей для сравнения видов транспорта, где t = 1,…,T, l = 1,.., L.

Выходными данными является вид ТР, удовлетворяющий требуемым критериям: количество видов транспорта; единый оператор перевозки; оплата перевозки; схема взаимодействия участников ТП; количество договоров; ответственность за груз (обеспечение безопасности груза); количество ответственных лиц; время доставки; стоимость перевозки; надежность соблюдения графика доставки груза; частота отправлений; способность доставить груз в любую точку; возможность выбора логистического партнера; время оформления заявки на транспортировку.

Алгоритм OPT_Route используется для подзадачи формирования рациональных маршрутов, который базируется на процедурах локального поиска с чередующимися окрестностями [1].

Входные данные: интерактивная карта автомобильных дорог ; БД: внутренние данные (списочный парк TC V` = {1,…,k} с различной грузподъемностью Qv = {Q1,…,Qk}в каждом депо; матрица фиксируемой стоимости использования ТС cfv; набор (пунктов) клиентов E = {ei,...,^ } (спрос на ГП 1клиента qil, предпочтительное время обслуживания [ai,bi], сервисное время обслуживания клиентов s’);

информация о депо D ={d 1 ,...,d_Nprod} (вместимость депо R d , предпочительное время возвращения в депо maxTV^v, время отправления Т^ TC v из депо); допустимый уровень риска ДТП на маршрутах R max , возможный уровень качества дорог W ij («возможный класс дорог на участках маршрута»); допустимая оплата за платные дороги на маршруте Сp^max; штрафная стоимость при нарушении времени обслуживания клиентов p i ; штрафная стоимость при нарушении времени обслуживания клиентов p_i;штрафная стоимость p^v для нарушения возвращения времени в депо); C^6lst - стоимость пройденной единицы расстояния для любого TC_v; стоимость С ^ пройденной единицы расстояния для любого TC^v; стоимость C t пройденной единицы времени для ТС v; внешние данные (координаты клиентов на карте; координаты депо на карте; матрицы расстояний между пунктами; время в пути между пунктами f t ; матрица платы на участках дорог сp ij , матрица типов дорог на участках w ij , матрица КА ДТП на участках дорог p_i j , ущерб d^v от ДТП на участках дорог).

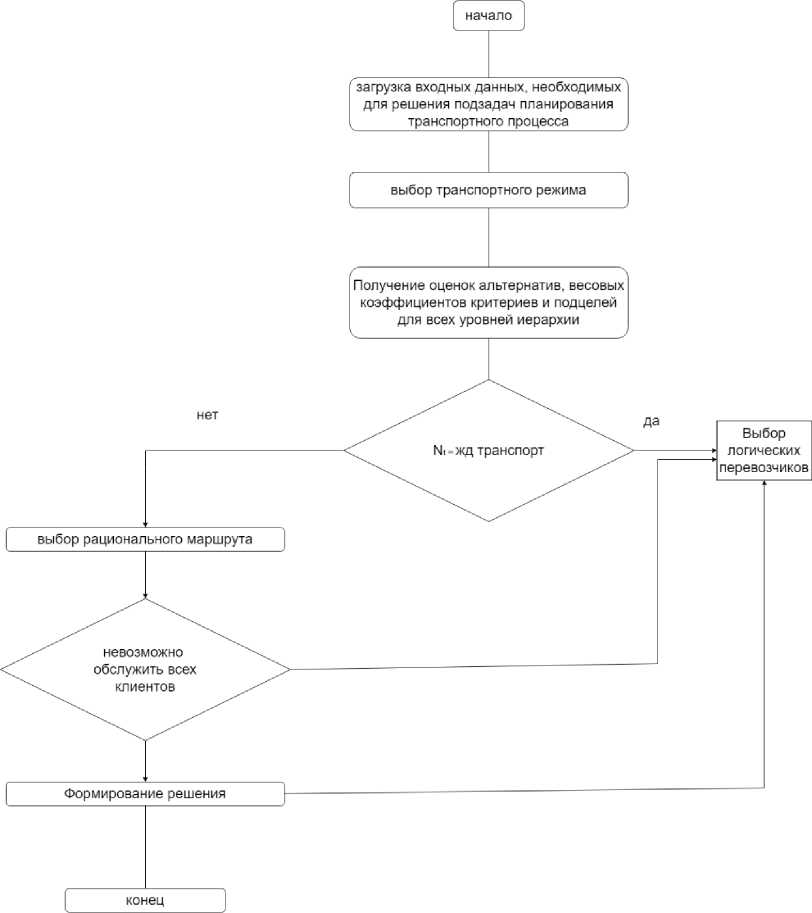
Рисунок 1 – Общая схема планирования транспортного процесса перевозки ГП

Выходными данными является набор r^cost = {r 1 ,…,r i ,…,r l } рациональных маршрутов транспортировки готовой продукции автомобильным транспортом

Метод Chcarrier используется для подзадачи Выбора ЛП, который базируется на методе замещений и предпочтений Кини - Райфа [30,43].

Входные данные: Р - количество перевозчиков; К — количество критериев оценки перевозчиков; Zp - значения по каждому критерию к для каждого ЛП р, где к = 1,...,К, р = 1,...,Р.

Выходные данные: ЛП, удовлетворяющий требуемым критериям. В основу метода выбора транспортного режима (Ch_transport) положен метод Саати (рисунок 2). Метод обеспечивает выбор способа транспортировки и вида транспорта. При этом выбор должен удовлетворять критерию наилучшей интегральной оценки.

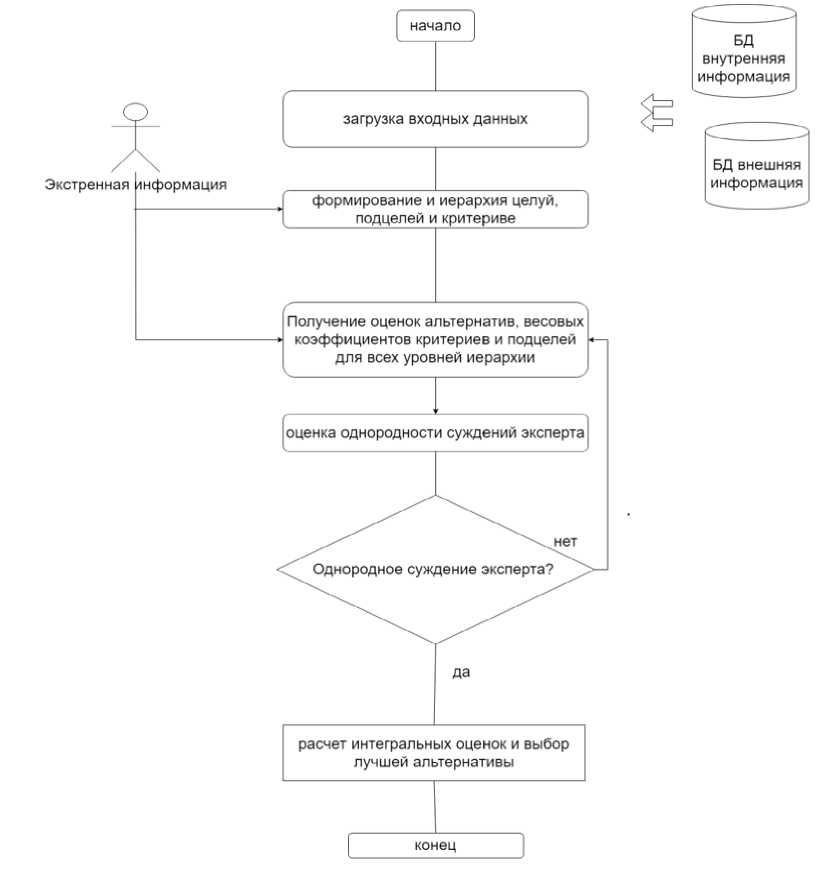
Рисунок 2 – Общая схема метода иерархии Саати

Вход :N s ={N t ….N s }; V s ^f = [V^….VQ, где 5 = 1….5, / = 1,..,F;

Nt = [Nx NT};Vtl = [Vl VkT], где t = 1 TJ = 1,..,1

Выход: вид транспортного режима.

Шаг 1. Формирование иерархии целей, подцелей и критериев.

Построим иерархию выбора ТР (рисунок 3).

Цепь. Выбор транспортного режима

Подцель!: Выбор способа транспортировки

Критерий 1.1: Количество видов транспорта 1)

Критерий 1J: Количество операторов перевозки (Чу )

Критерий 13: Оплата перевозки Л/f)

Критерий 1.4: Схема взаимодействия участников ТП |VS4)

Критерий 15 Количество договоров (V,5)

Критерий 1.6: Ответственность за груз 1VS6)

Подпеть 2: Выбор вида транспорта

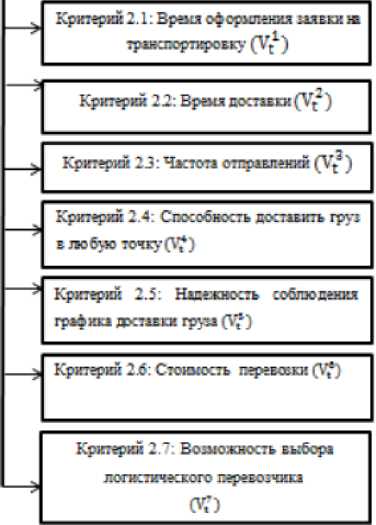
Критерий 1.7: Количество ответственных ™i(V,7)

Рисунок 3 - Иерархия выбора транспортного режима

Шаг 2. Получение оценок альтернатив (ТР), весовых коэффициентов критериев и подцелей для всех уровней иерархии.

Для формализации знаний эксперта по поводу сравнительной важности расположенных на одном уровне элементов иерархии относительно вышележащего элемента иерархии используется 5 - балльная шкала (таблица 1), в отличие от 9-балльной шкалы Саати [2] в предложенной шкале нет промежуточных оценочных значений [2, 3].

Таблица 1 – Шкала для парного сравнения подцелей, критериев и альтернатив ТР

Степень значимос	Определение	Объяснение
1	Одинаковая значимость	Две подцели, два критерия или две альтернативы вносят одинаковый вклад в достижение цели
3	Некоторое преобладание значимости одного действия над другим (слабая значимость)	Существуют соображения в пользу предпочтения одной из подцели, одного критерия, одной альтернативы однако эти соображения недостаточно убедительны
5	Существенная или сильная значимость	Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность одной из подцели, одного критерия, одной альтернативы
7	Очевидная    или    очень сильная значимость	Убедительное свидетельство в пользу одной из подцели, одного критерия, одной альтернативы перед другой подцелью, критерием, альтернативы
9	Абсолютная значимость	Свидетельства в пользу предпочтения одной подцели, критерия, альтернативы другой подцели, другому критерию, другой альтернативы в высшей степени убедительны

На основе этой шкалы ЛПР попарно сравнивают альтернативы по критериям. Результат заносятся в матрицу парных сравнений [2, 3]. Рассмотрим подробнее процедуру попарного сравнения альтернатив на примере критерия Количество видов транспорта (таблица 2).

Таблица 2 – Сравнение экспертом альтернатив по критерию 1.1

№ альтернативы	А1	A2	A3	A4	A5	A6
А1	1	k 1 /k 2	k 1 /k 3	k 1 /k 4	k 1 /k 5	k 1 /k 6
А2	k 2 /k 1	1	k2/k3	k 2 /k 4	k2/k5	k 2 /k 6
A3	k 3 /k 1	k3/k2	1	k 3 /k 4	k 3 /k 5	k 3 /k 6
А4	k 4 /k 1	k 4 /k 2	k 4 /k 3	1	k 4 /k 5	k 4 /k 6
А5	k 5 /k 1	k 5 /k 1	k 5 /k 3	k 5 /k 4	1	k 5 /k 6
А6	k 6 /k 1	k 6 /k 1	k 6 /k 3	k 6 /k 4	k 6 /k 5	1

Где отношение k i /k j - выражает мнение эксперта о том, во сколько раз альтернатива / лучше (хуже) альтернативы j.

Аналогичным способом необходимо сравнить альтернативы по всем критериям (критерии 1.2-1.7 и критерии 2.1-2.7). После получения всех сравнительных таблиц, необходимо рассчитать конкретные оценки альтернатив по каждому критерию, применяя для этого подсчет строчных сумм матрицы парных сравнений и нормирование полученных значений (таблица 3). Сумма весовых коэффициентов одного уровня иерархии равна 1.

Таблица 3  – Вычисления весовых коэффициентов для каждой альтернативы по критерию 1.1

№ П ТТТ ГТ.ГЬ^ТТП^ТГК.Т Т---	А1	А2	A3	А4	А5	А6	трочная сумма	Нормированное значение критерия
А1	1	k 1 /k 2	k 1 /k 3	k 1 /k 4	k 1 /k 5	k 1 /k 6	6 в1^ Ki j = 1   j	В 1 /В sum
At							B q ^EK j=1    j	В t /В sum
А6	k 6 /k 1	k 6 /k 2	k 6 /k 3	k 6 /k 4	k 6 /k 5	1	B 6 ]EK 6 j=1    j	В 6 /В sum
Сумма1							Bsum = E n =1 B n

Для получения весовых коэффициентов альтернатив по критерию 1.1 при оценивании несколькими экспертами в качестве весового коэффициента для элемента иерархии рассматривается среднее геометрическое весовых коэффициентов Bi, полученных по матрицам парных сравнений каждого из

^11    О    О экспертов В[ =  В1 „В. „.В^, где Q - количество экспертов.

Получение сравнительных оценок, весовых коэффициентов критериев и подцелей происходит аналогично получению оценок альтернатив ТР (таблицы 3.2, 3.3).

Шаг 3 . Оценка однородности суждений эксперта.

Для оценки однородности суждений эксперта необходимо использовать отклонение величины максимального собственного значения Л_тах от порядка матрицы п.

Однородность суждений оценивается индексом однородности ИО [или отношением однородности ОО: ИО = (X max — п)/(п — 1), ОО = ИО/М(ИО), где М(ИО) - среднее значение (математическое ожидание) индекса однородности случайным образом составленной матрицы парных сравнений, которое основано на экспериментальных данных.

В качестве допустимого значения используется значение ОО не более 0,1. Если для матрицы парных сравнений отношение однородности ОО больше 0,1, то это свидетельствует о существенном нарушении логичности суждений эксперта. Поэтому эксперту предлагается пересмотреть данные, использованные для построения матрицы. Оценка однородности производится для всех матриц парных сравнений.

Шаг 4 . Расчет интегральных оценок для альтернатив.

Основная идея данного метода заключается в следующем: вначале в процессе кластеризации все клиенты с учетом дистанции между депо и клиентами относятся к определенному кластеру; в каждом кластере с использованием процедур локального поиска с чередующимися окрестностями находится набор рациональных маршрутов, учитывающий условия и ограничения; последним этапом методики является нахождение показателей (расход бензина, пробег ТС) для найденных маршрутов (рисунок 4).

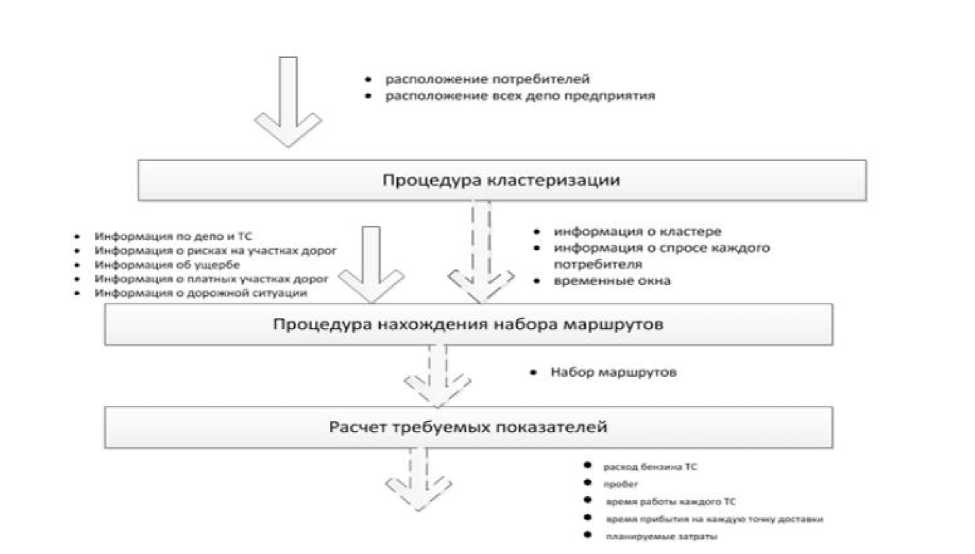
Рисунок 4 – Схема решения задачи формирования рациональных маршрутов в системе планирования транспортного режима при перевозках готовой продукции

Формирование рациональных маршрутов базируется на классических алгоритмах: алгоритм Кларка и Райта (Clarke and Wright Algorithm) и алгоритм локального поиска с чередующимися окрестностями (Variable Neighborhood Search). Классические схемы алгоритма Кларка и Райта и алгоритма локального поиска с чередующимися окрестностями для решения задач маршрутизации транспорта представлены в приложении Е и Ж соответственно. В связи с особенностями содержательной поставки задачи формирования рациональных маршрутов в работе данные алгоритмы были модифицированы.

Рассмотрим алгоритм ОРТ Route для выбора рациональных маршрутов в системе управления транспортным процессом при перевозке ГП.

Схема алгоритма ОРТ Route

Входные данные: Е = {e i ...,e_Ncust }, D = {d i ,..,% _rod }, A = {A_b..., ^AN _as ^},

V = {1,.., k], Q v = {Q t ,^,Q k }, q il , [a i , b i ],  S_t ^v , R d , maxTV v , R^max, W_y,

Cp^max, p i , p^v, c ^ , t . , cp ij W ijt P ij , d^v,cf v c dist , c^. , T^,

Выходные данные: rcost = {r1,…, ri,.., r1}.

Процедуры Кластеризации выглядит следующим образом:

Шаг 1 . Формирование списка всех клиентов CL и списка всех депо Dep.

Шаг 2 . Разделение списка Dep на N prod кластеров, где N prod -количество депо.

Шаг 3 . Формирование кластера К i выбираем клиента і из списка всех клиентов CL.

Шаг 4 . Ранжирование списка депо d по расстоянию от выбранного клиента і.

Шаг 5 . Выбор депо d, минимально отдаленного от клиента і.

Шаг 6 . Добавление клиента і в кластер K t .

Шаг 7 . Переход к следующему клиенту.

Шаг 8 . Выполнение шагов 3-7, пока список клиентов CL не будет равен «0».

Пошаговое описание Процедуры Rat Route представлено ниже.

Шаг 1 . Формирование ограничений для проверки допустимых найденных маршрутов из возможных ограничений, указанных в разделе 3.1, главы 3.

Шаг 2 . Формирование первоначального допустимого набора маршрутов для каждого кластера, с использованием модифицированного алгоритма Кларка и Райта.

Шаг 2.1. Построение матрицы выигрышей для всех клиентов, аналогично шагу 1 стандартного алгоритма Кларка и Райта.

Шаг 2.2. Нахождение максимального выигрыша в матрице выигрышей.

На матрице выигрышей находим ячейку (i*, j*) с максимальным выигрышем Smax (2):

^ тах = maxfj s(i,j) = s(i * ,j * ),

При этом должны соблюдаться следующие три условия:

• —   пункты i* j* не входят в состав одного и того же маршрута;

• —  пункты i* и j* являются начальным и/или конечным пунктом

тех маршрутов, в состав которых они входят;

• —   6ij - логическая переменная - статус ячейки (i * ,j*), которая может

принимать следующие значения: 5 ф = 1, если ячейка (i * j*) посещена на предыдущих шагах, и 6 ij = О, если ячейка не была посещена ни разу. При этом считается, что ячейка (i*,j*) не заблокирована. Ячейка (i*,j*) является заблокированной, если спрос клиента і полностью удовлетворен q_i j ' = 0, который вычисляется следующим образом q il ' = q il - i V ,

Где q ii - спрос на ГП I клиента i;

• y iv - спрос i - ого клиента, удовлетворенного ТС v;

• q il ' -обновленный спрос на ГП l клиента i.

Если удалось найти такую ячейку, которая удовлетворяет указанным условиям, то переход к шагу 2.3, иначе переход к шагу 2.16.

Шаг 2.3. Проверка грузоподъемности ТС (3.19)

^_eeEq_eiY = - R d X deo Х Ц < 0, где I = 1,™, L.                        (3.19)

Шаг 2.4. Сумма спроса q el клиентов на ГП I не может превышать вместимость R d обслуживающего депо d для ГП I (3.20):

Х И=1 Х_Е е _ЕЧ_Е 1 У_е^т - R d S den X S < о, где I = 1,-, L.                  (3.20)

Шаг 2.5. Вычисление времени прибытия в пункты потребления и отбытия из пунктов потребления.

Шаг 2.6. Назначение штрафной величины р., если временное окно [а е ,Ь е ] обслуживания клиента є было нарушено (3 – 4):

Да" > (a, - T") x У"

ДЬ" > (T"" - Ь,) x У"(4)

Шаг 2.7. Назначение штрафной величины pv,  если время возвращения ТСv в депо d было нарушено (5)

ДТ^Г - maxTVv) x X^TVV > TVV - maxTVv) x Xva.(5)

Шаг 2.8. Выбранные маршруты могут включать в себя дороги типов

• А, Р, М: w_t j * Xj-j <  w_t j для всех v = 1,..,k; i,j е V, w_t j e{N,K,A,P,M} ^ w_t j ^{е (1,}2^,3,4,⁵⁾, W jj = 3.

Шаг 2.9. Плата за используемые дороги на выбранном маршруте не должна быть выше, чем максимально допустимая оплата за платные дороги (6)

Z iey Z iey ср^х % <  Cp max , rgev= 1,_,k.                                   (6)

Шаг 2.10. Риск ДТП маршруте должен быть не больше допустимого уровня риска (7)

R v = Z iev Z iev P iy * X^V = 1,..,k; ZievZievPij * X ^ <  R^max .         (7)

Шаг 2.11. Объединение маршрутов.

Производим объединение маршрутов 1 и 2 в один общий маршрут. Будем считать, что пункт і * является конечным пунктом маршрута 1, а пункт j* - начальным пунктом маршрута 2. При объединении маршрутов 1 и 2 соблюдаем следующие условия:

• —    последовательность расположения пунктов на маршруте 1 от начала и до пункта і* не меняется;

• —    пункт і* связывается с пунктом j*;

• —    последовательность расположения пунктов на маршруте 2 от пункта j* и до конца не меняется;

• —    общий маршрут удовлетворяет ограничению на вместимость.

Если вышеуказанные условия выполняются, то переход к шагу 2.12, если нет-к шагу 2.13.

Шаг 2.12. Повторение шагов 2.1-2.11.

Повторяем шаги 2.1 - 2.11 до тех пор, пока при очередном повторении не удастся найти S_max который удовлетворяет условиям из шага 2.2.

Шаг 2.13. Вычисление ущерба компании от ДТП на выбранном маршруте определяется следующим образом D^v = d^vR^v.

Шаг 2.14. Вычисление пройденного расстояния вычисляется согласно формулам (2.6) - (2.9)

Шаг 2.17. Расчёт целевой функции.

Шаг 3 . Поиск рационального маршрута с помощью процедур локального поиска с чередующимися окрестностями.

Введем дополнительные параметры: количество итераций k в кластере, время итерации t max , окрестности N_k,k = к 1 , .^,к_тах различных структур с : = i, i = 1,2,3,4,5.

Выходным параметром будет набор маршрутов   r^cost  =

• {7 1 , ^ ,7 ^ , ^ ,7 1 } со значением целевой функции L.

Шаг 3.1. Использование полученного решения на предыдущем шаге - набора маршрутов r^cost = {7 1 , ..., r_it ..., 7 1 } со значением целевой функции L.

Шаг 3.2 . Выбор случайным образом тип структуры окрестностей с : = і, і = 1, 2, 3,4, 5 для построения окрестности решений:

• с:    = 1 (Demand move);

• с :    = 2 (Swap Move);

• с :    = 3 (Shift Move);

• с :    = 4 (Swap);

• с :    = 5 (opt2).

• 3.2.1    положить k :=1;

• 3.3.2    повторять до момента, пока k < k max .

Стратегии построения представленных типов окрестностей решения для нахождения маршрута минимальной стоимости отражены в приложении И.

Шаг 3.3. Применение процедур локального поиска для поиска допустимых маршрутов r^cost = {7 1 , .„, 7_t, .„, 7 1 }.

Выбрать случайным образом из окрестности Nk решение r' Е Nk(r). Применить методы локального поиска от начального решения r`, найти решение r``, полученный локальный оптимум обозначить r``. Если L(r``) < L(r`) , то полагается r:= r``, при k:= 1, иначе k := k + 1.

Шаг 3.4. Проверка «новых», улучшающих первоначальное решение, маршрутов r^cost = {7 1 , ^ ,7 [ , ^ ,7 1 } из окрестностей, на нарушение выбранный ограничений в 3.1.

Шаг 3.5. Выбор лучшего решения, используя критерий – Best Improvement.

После нахождения набора маршрутов необходимо рассчитать следующие показатели с помощью Процедуры Activities Route:

• —   расходная стоимость потраченного топлива;

• —   амортизационные затраты;

• —   расходы на резину;

• —   расходы на материалы, запасные части и техобслуживание;

• —   дополнительная плата за маршрут водителей;

• —   накладные расходы;

• —   пробег ТС;

• —   время отправления и время прибытия.

Пошаговое описание Процедуры Activities Route представлено ниже. Шаг 1. Вычисление расходной стоимости потраченного топлива (8):

Cost Fue i r = Fuelr. x Cost Fuel ,                                                 (8)

где Cost_Fuel - цена 1 литра дизельного топлива

Fuel ri . - расход топлива в литрах

Шаг 2. Вычисление фиксированной стоимости использования ТС cf^v , которая включает в себя амортизационные затраты, расходы на резину, расходы на материалы, запасные части и техобслуживание.

Шаг 3. Дополнительная плата водителей Cost_add вычисляется по формуле 9: