Информационное моделирование системной динамики поршневых двигателей внутреннего сгорания

Введение. Поршневой двигатель внутреннего сгорания (ДВС) является основным агрегатом современных автотранспортных средств, поэтому топливная экономичность и токсичность отработавших газов (ОГ) имеют первостепенное значение. Отсюда растущий интерес к информационным моделям рабочего процесса ДВС как инструменту интерпретации данных, оптимизации конструкции, средству поиска альтернативного моторного топлива [1, 2].

При моделировании внутрицилиндровых процессов приходится преодолевать «проклятие размерности», проблему разнородности и разномасштабности процессов, аккуратно описывать «обостренные» режимы и формирование структур. Важно отработать методики агрегирования фрагментных моделей таким образом, чтобы результат «склеивания» наследовал регуляризующие свойства ключевых элементов [3].

Попытки рассчитать токсичность поршневого ДВС при помощи компьютерных моделей [4–5] лишь отчасти оправдали ожидания авторов: хорошо воспроизводя выбросы СО, углеводородов C x H y , сажи и сернистых соединений, они давали на два порядка заниженные концентрации NO в ОГ. Поскольку в первых моделях внутрицилиндрового горения в двигателе азотная кинетика не учитывалась, проблема рассчитать содержание NO в выхлопе связывалась с химической не-равновесностью рабочего тела, которое полагалось параметрически однородным. Впоследствии кинетическая схема [5] была дополнена реакциями с участием азота, но для расчета концентрации NO в ОГ этого оказалось недостаточно.

Ключевые идеи, допущения, математическая формулировка задачи.

Отработана следующая гипотеза. Если макроскопически трехзонные кинетические модели не позволяют адекватно воспроизвести токсичность ДВС по NO, причиной может служить только пространственное переосреднение, т.е. замена истинного поля параметров Х ( r, t ) средними по пространству величинами, например, < Х ( t )> или X (< r>, t ). Это приводит к тому, что важные для целей моделирования связи не отражаются моделью. В математической формулировке задачи использованы обозначения: Х = { c 1 , c ₂, .., 7 } - псевдовектор, объединяющий концентрации компонентов c i , см -3 , и температуру T, К; r = { r 1 , r ₂, r 3 } - пространственная вектор-переменная, {м, м, м}; t – время, с.

Информационная модель (ИМ) упрощается, если в системе имеются и выявлены малые или, наоборот, большие параметры [3].

Схематизация горения в двигателе: модель «реакции-перенос». Основополагающие предположения усовершенствованной модели унаследованы от прототипов [4, 5] и формулируются следующим образом:

• –    топливно-воздушный заряд химически и термодинамически однороден;

• –    впрыскиваемое топливо монофракционно, а его условная химическая формула C 14 H 30 (дизельное) или C 8 H 18 (бензин);

• –    химические аспекты горения хорошо укладываются в кинетическую схему, ограниченную элементарными реакциями между C-H-O-содержащими веществами с тремя и менее атомами углерода, а также несколькими брутто-реакциями крекинга исходных углеводородов;

  – турбулентные эффекты сводятся к ограничению скорости элементарных химических

процессов темпом переноса реагентов в зону тепла из зоны пламени;

• –    испаряется жидкое диспергированное топливо диффузионно;

• –    теплообмен излучением незначителен.

Поскольку диффузия, теплопроводность и реакции – равнозначные «игроки» в процессе формирования пламенных структур, кинетические члены в уравнениях непрерывности и энергетического баланса подверглись «мелкомасштабному» осреднению. Для учета макроскопической параметрической неоднородности топливно-воздушной смеси осуществлено разбиение заряда на три взаимодействующих зоны, внутри каждой из них рабочее тело полагается однородным. Скорость межзонного обмена термохимическими характеристиками определяется как «качество смесеобразования» с помощью полуэмпирической зависимости.

Энергетическая открытость модели обеспечивается заданием реалистичных условий теплоотдачи со стороны заряда (горящей топливно-воздушной смеси) в стенки камеры сгорания и внешнего силового (или, точнее, моментного) нагружения ДВС. Теплообмен задается уравнением Ньютона–Рихмана, а нагрузка – известными уравнениями кинематики кривошипно-шатунного механизма [6] под действием внешних сил, препятствующих свободному вращению коленвала. В модели эти силы имитирует линейная комбинация сухого трения и гидродинамического сопротивления движению, которое выбрано пропорциональным частоте вращения коленвала.

В разработанной авторами информационной модели (ИМ) рабочего процесса ДВС химизм горения углеводородного топлива описывается совокупностью более чем 400 микроскопически обратимых элементарных реакций, кинетические характеристики которых взаимно согласованы в рамках общего термохимического потенциала реагирующей газофазной среды [7, 8]. Эта важная особенность представленной ИМ качественно отличает ее от известных аналогов и прототипов, в динамике которых не исключены артефакты.

Собственно внутрицилиндровый химизм, его связь с динамикой и теплообменом описывается системой дифференциальных уравнений dX

— = f ( x ) + s ( x , t) , dt где f - скорость изменения термохимических параметров заряда X, {см-3- c-1, см-3 ■ c-1, ..., К ■ c-1}; S- темп обмена термохимическими параметрами между зарядом и «резервуаром», {см-3- c-1, см-3 ■ c-1, ..., К ■ c-1}.

Система (1) подразумевает пространственное осреднение динамических переменных, причем в самом общем виде. Уравнения внутрицилиндровой динамики ДВС и сопряженных процессов, осреднением которых получены (1), подробно описаны в работах [7, 8], а основная идея метода их осреднения описана ниже. Ключевой особенностью описанной модели является двухмасштабное осреднение динамических переменных, объединяющее параметрическое осреднение кинетических уравнений на уровне пламенных диффузионно-реакционных структур (с учетом турбулентного разлохмачивания последних) и осреднение на уровне квазиооднородных макрообъемов горящей топливно-воздушной смеси (ТВС) заряда.

Микромасштабное осреднение эволюционных уравнений основано на следующих научных результатах. Распространяющееся по однородной горючей смеси пламя служит классическим примером автосолитонов [8]. Выделяющаяся в процессе горения среды внутренняя энергия «собирается» вследствие конкуренции нелинейности и диффузионного переноса в бегущую локализованную структуру (волну). Скорость распространения волны горения – среднегеометрическая величина между обратным временем химической реакции и эффективным коэффициентом диффузии вещества и/или тепла в горючей среде. Поэтому явной формой эволюционных уравнений динамики поршневого (одноцилиндрового) ДВС, осредненных по структуре/масштабу пламенной зоны, являются:

^ = f *( n, p , T ) + F_t(t ) ; dt

dT ;L ft*(n,p,T){HJCv -T} + dt         ^ n где

dA dt

dQ         dA dQ w   dQ ph

• — q ⁽ t )                             ^;

dt            dt dt dt sin Qt + у /2sin 2Q t

• 2 -^j- + 0,5(1 - cos Q t + у /2sin² Q t

Q = a S , ( T - T , ) ;

dt

Q ph

"d T - LF ⁽ t ) , dn     dn _i

"dt "^ "dt '

dm

17 = ^G ( t )

dt

—

3 D f

Q nRT ;

F . ( t ) = 5 , , j

Л ²

3 D f m

m f ;

Л ц f

f

;

I d ² ф / dt ² + ( k 1 + k ₂| d ф / dt |) d ф / dt + P ( ф ) S_p r ( ф ) = 0 ; Р ( ф ) = k б RT ( ф ) /V ( ф ) ;

[ j * ( n , p , t )] - * = [ fchem ( n , p , t )] - * + [ jf f ( n , p , t )] ^{- 1},

• j df ( n , p , T ) = ^2s i ^{gn{ j (} n , ^P , T ^{+ T} a ^{d /2)}} 1 V D Re^1,5 n ; If ( n , P , T + T ad /2) I;

n = {ni}, ni = ci /p[молекул/г] - концентрация компонентов (p - плотность газа, г/см3); Re - число Рейнольдса; Fi - внешние источники газообразного вещества (при впрыске); q - доля теплового потока, не связанная с химическими реакциями; mfи Lf- соответственно масса жидкой фазы и теплота испарения; цj - молекулярный вес j-го газового компонента; Sw и l - мгновенное значение площади поверхности теплообмена и характерного линейного размера камеры сгорания (КС); у. и е - отношение радиуса кривошипа к длине шатуна и геометрическая степень сжатия; a, T, - усредненные коэффициент теплоотдачи, температура поверхности КС; Df, Л = Л(G) и G(t) - коэффициент диффузии паров топлива в вакуум, средний диаметр капель при распылении форсункой и массовая скорость впрыска топлива; 5ij - символ Кронекера; R - универсальная газовая постоянная; I - приведенный момент инерции нагруженного ДВС; P(ф), Sp и r(ф) - соответственно мгновенное давление в камере сгорания, площадь поршня и имеющая размерность длины функция передачи поступательного усилия во вращение (это слагаемое в уравнении (11) соответствует одноцилиндровому ДВС); ф - угол поворота, град. ПКВ и Q = dф/dt - частота вращения коленвала; k 1 и k2 - коэффициенты сопротивления вращению; kБ - постоянная Больцмана; прочие обо- значения соответствуют принятым в теплотехнике.

Фигурирующий в уравнениях (2)–(12) комплекс f * агрегирует два параллельных канала химических превращений: f chem – медленные реакции, протекающие синхронно во всех точках камеры сгорания как в реакторе идеального смешения, и f diff – быстрые процессы во фронте пламени, темп которых ограничивается турбулентной диффузией. Раскрывающие смысл (2)–(12) алгебраические соотношения уравнивают роли реакционного и транспортного каналов в совокупном процессе образования/гибели i-го вещества. В соответствии с (2)-(12) при идеальном перемешивании все вещества образуются равномерно в объеме камеры сгорания, а при сильно затрудненном – во фронте горения. Мерой перехода того или другого канала образования вещества в ранг доминантного служит степень турбулизации заряда. Предложенная техника позволяет достаточно аккуратно учитывать роль диффузионных процессов при горении в ДВС, используя обыкновенные дифференциальные уравнения в качестве базового математического инструмента. Ес- тественно, в пламени реакции протекают при повышенной температуре: ее скачок ограничен адиабатической температурой сгорания ТВС в локальных условиях Tad и в нашей модели полагается равным Tad/2.

Кроме того, поскольку нет универсальной связи между коэффициентом турбулентной диффузии D turb и числом Re, в нашей модели использована зависимость D turb ~ Re ^3/2 , промежуточная между известными предельными приближениями, мелко- и крупномасштабных пульсаций D turb ~ Re и D turb ~ Re ² .

Определенным недостатком предложенных здесь уравнений горения является отказ на данном этапе от осреднения скоростей реагирования по Фавру на масштабах пламенной зоны [9]. Оправданием такого упрощения нашей модели служит достаточно интенсивная турбулизация, следовательно, заметное размытие реакционной зоны в пространстве. Согласно специально выполненным оценкам, в условиях ДВС чувствительность констант скоростей реакций к изменениям температуры заметно превышает их чувствительность к плотности реагирующего газа.

Если ограничить осреднение уравнений химизма только мезотранспортными процессами в пламени, концентрация ряда токсичных продуктов сгорания оказывается заниженной. Это касается как продуктов неполного сгорания СО и С х Н у , так и побочных продуктов окисления NО x . Причина кроется в том, что выход этих продуктов определяется крупномасштабной параметрической неоднородностью ТВС, а не кинетикой гомогенных реакций.

Для приведения модели в соответствие реальному положению вещей в ней использовано предположение о существовании в пределах заряда ТВС трех параметрически однородных зон:

• -    с номинальным коэффициентом избытка воздуха а 1 = а , в которой сгорает x -я часть топлива (0 <  x < 1);

• -    коэффициентом избытка воздуха а ₂ = 0,7, где сгорает 1/2(1 - х) доля топлива;

• -    коэффициентом избытка воздуха а ₃ = 2 а - 0,7, где сгорает остаток топлива.

Итоговую концентрацию i -го компонента находим при помощи соотношения

< С> = ^ (1 - х ) C i ^0,7 + x C i^а + ^ (1 - х ) C i ^{2 а - 07} ,                           (13)

где верхний индекс при c i соответствует локальному коэффициенту избытка воздуха.

Для расчета качества смесеобразования х нами предложена формула

X = th ( т chem / т gd ) = th [ D turb Е H i / ( 1 2 Е | dHi / d 1 1)] ,                              (14)

где τ chем и τ gd – характерное время химического окисления и механического перемешивания заряда.

Внесение коррективы в исходную модель значительно улучшило согласие рассчитываемых величин c i с известными из эксперимента тестовыми данными.

Параметры модели S _w, 1 и Re (соответственно D turb ), безусловно, являются конструктивно определенными функциями времени t .

Развиваемая в соответствии со схемой (рис.1), модель позволяет не только надежно определять энергетические (интегральные и мгновенные) характеристики рабочего цикла различных типов ДВС, но также содержание в ОГ СО, С х Н у , NO, RCOH, воспроизводить тонкости образования токсичных веществ на переходных режимах.

+

Энергетические показатели

Классическая термодинамическая модель рабочего процесса

+ нестационарность

+ агрегация диссипативных структур (сингулярные возмущения)

Модель с ассоциированным описанием фронта пламени

+

+

Переходные режимы Токсичность по СО

Токсичность по C n H m , C, RCOH

Токсичность по NO

Токсичность по ПАУ – C 20 H 12

Энергетика + динамика + суммарная токсичность отработавших газов

Рис.1. Эволюция модели рабочего процесса поршневого ДВС [4–8]

Авторами также ведутся работы по расширению номенклатуры токсичных компонентов в выхлопных газах за счет сажи и бенз(а)пирена C 20 H 12 .

Результаты вычислительного эксперимента и их интерпретация. Адекватность созданной модели оценим, сопоставляя рассчитанные с ее помощью характеристики рабочего процесса ДВС и данные технического эксперимента. Соответствующие результаты для распространенного тепловозного дизеля 1Д49 приведены в табл.1.

Таблица 1

Некоторые интегральные, экстремальные и мгновенные характеристики рабочего процесса в дизеле 1Д49 в режиме номинальной мощности

Параметры	Расчет	Эксперимент
Среднеиндикаторное давление, атм	19,4	20,1
Индикаторная мощность двигателя, кВт	4620,0	4740,0
Индикаторный КПД, %	44,2	45,1
Удельный расход топлива (инд.), г/кВт ⋅ ч	195,0	186,0
Максимальное давление, атм	136,0	130,0
Максимальный темп нарастания давления, атм/град ПКВ	3,9	–
Максимальная температура, К	1630,0	–
Максимальная скорость роста температуры, К/град ПКВ	61,0	–
Доля выделившегося тепла заряда до P max , %	49,0	–
Максимальное содержание СО в заряде, %	1,7	–

Эти данные свидетельствуют, что доступные для экспериментальных измерений параметры рабочего цикла надежно рассчитываются на основании предложенного авторами кинетического подхода. Кроме того, разработанная схема вычислений позволяет определять ряд не измеряемых, но важных для практики эксплуатации ДВС мгновенных и интегральных параметров рабочего процесса (выделены в табл.1 жирным шрифтом).

Для целей оптимизации впрыска и газообмена в поршневом ДВС важны интегральные и мгновенные энергосиловые показатели рабочего процесса (давление и температура в камере сгорания), а также токсические характеристики заряда и ОГ. Разработанная для управления электромагнитной системой клапана математическая модель внутрицилиндровых процессов позволяет рассчитывать определяющие параметры рабочего тела в динамике с большей (механические) или меньшей (токсические по оксиду азота) степенью достоверности. В табл.2–4 приведены результаты энергосиловых расчетов для трех представительных режимов двигателя ВАЗ–2108: скорость вращения коленвала составляет на этих режимах 1000, 2000 и 4000 мин^–1, коэффициент избытка воздуха α = 1.

Таблица 2

Параметры рабочего процесса двигателя ВАЗ–2108

Коэффициент избытка воздуха, доля объема	1 0,8	0,7 0,2	1,3 0,2	Среднее значение
1	2	3	4	5
	5,93	5,91	1,34	5,47
Среднеиндикаторное давление, атм	6,47	5.82	1,31	5,89
	5,86	5.67	1.59	5,41
	16	15,9	3,6	14,8
Индикаторная мощность, кВт	34	31,4	7,1	31
	63	61	17	58,2
	19	10	5	16,7
Угол поворота коленвала при максимальном давлении в КС,	12	5	4	10,5
град ПКВ после ВМТ	15	2	5	12,7
	59	73	29	57,4
Максимальное давление, атм	69	77	31	66
	68,7	78,4	32,7	66,1
	16	9	-13	12,4
Угол поворота коленвала при максимальной скорости нарастания	-13	2	-11	-11,3
давления в КС, град ПКВ после ВМТ	10	-9	-12	6

Окончание табл.2

1	2	3	4	5
	6,95	9,44	0,67	6,57
Максимальная скорость нарастания давления в КС, атм/град ПКВ	11,8	9,8	8,5	11,3
	5,75	8,09	8,98	8,71
Угол поворота коленвала при максимальной средней температуре	25 23	10 6	23 18	23,3 20,8
заряда, град ПКВ после ВМТ	15	2	22	14,4
	2240	2193	925	2103
Максимальная средняя температура рабочего тела, К	2306	2175	942	2157
	2265	2135	1009	2126
Максимальная скорость нарастания температуры заряда, К/град ПКВ	290	299	9	263
	373	276	13	327,3
	204	225	14	187
	0,05	0,03	0,23	0,09
Доля теплоты цикла, выделившаяся до ВМТ	0,09	0,22	0,36	0,13
	0,12	0,59	0,36	0,19
Доля теплоты цикла, выделившаяся до момента,	0,88	0,98	0,33	0,84
	0,82	0,97	0,44	0,80
когда давление в КС максимально	0,98	0,97	0,45	0,93
Доля теплоты цикла, выделившаяся до момента,	0,99	0,99	0,80	0,97
	0,99	0,98	0,76	0,98
когда температура заряда максимальна	0,99	0,98	0,85	0,98

Примечание: тактность двигателя – 4; число цилиндров – 4; рабочий объем камеры сгорания – 400 см³; частота вращения – 1000 / 2000 / 4000 мин^–1; степень сжатия – 10; отношение радиуса кривошипа к длине шатуна – 0,25; давление в начале такта сжатия – 1,0 атм; температура в начале такта сжатия – 300 К; начало впрыска топлива – 20 / 30 / 35 гpад до ВМТ; длительность впрыска – 35 / 30 / 40 гpад; момент поджига заряда – 7 / 13 / 9 град до ВМТ; средний диаметр капель диз. топлива – 0,02 см; коэффициент диффузии паров диз. топлива – 0,1 см²/с; диаметр цилиндра – 8 см; ход поршня – 8 см; температура стенок камеры сгорания – 600 / 650 / 700 К; средний коэффициент теплопередачи – 0,01 Вт/см^2.К; обратное время диффузии кислорода в факел – 1000 / 1700 / 2500 1/с.

Приведенные в табл.2 данные согласуются с известными теоретическими положениями и экс- периментально установленными фактами. Развиваемая мощность монотонно возрастает с частотой вращения коленвала в интервале 1000– 4000 мин–1, в то время как крутящий момент (он пропорционален среднеиндикаторному давлению) максимален в интервале 2000–4000 мин–1. Увеличение темпа вращения коленвала сопровождается возрастанием доли тепла, выделившегося до ВМТ с 9 до 19 %, что также отвечает современному пониманию динамики внутрицилиндровых процессов.

Вклад трех макроскопических однородных зон заряда в силовую брутто-характеристику ДВС проиллюстрирован на индикаторной диаграмме (рис.2) для условий в средних строчках табл.2 (номинальный режим двигателя).

Усовершенствованная модель удовлетворительно воспроизводит кинетику СО-токсичности ДВС при изменении нагрузки, объема и закона подачи топлива. Кинетическая кривая [CO]( ϕ ) для одноцилиндровой версии двигателя 10Д100 при увеличении мощности от соответствующей холостому ходу до номинальной показаны на рис.3. Раз-

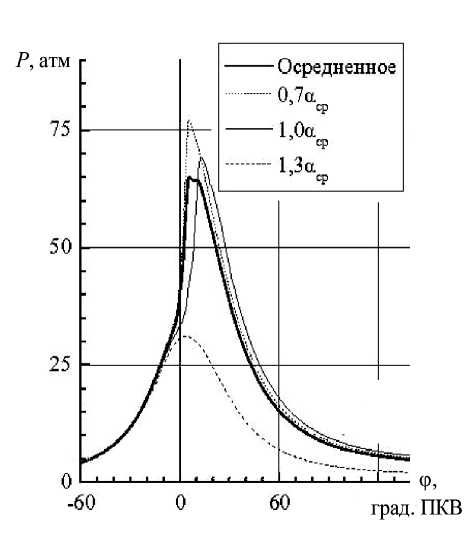
Рис.2. Парциальные индикаторные диаграммы для различных зон ТВС двигателя ВАЗ-2108 при частоте вращения коленвала 2000 мин–1 (при искусственно отключенном межзонном взаимодействии)

гон ДВС в вычислительном эксперименте осуществлялся увеличением цикловой подачи топлива в 4 раза; зависимость интенсивности впрыска топлива от угла поворота коленвала (ПКВ) не менялась.

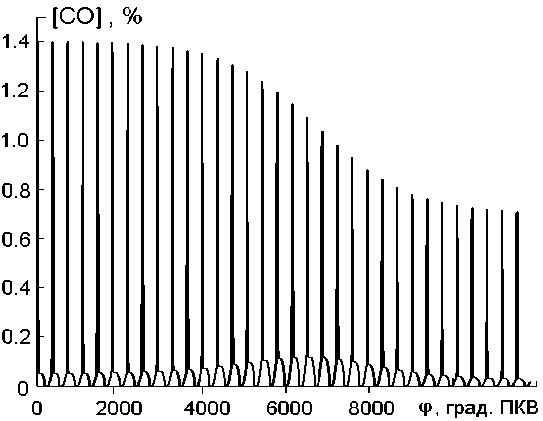
Рис.3. Переходный процесс в одноцилиндровом двухтактном дизеле: кинетическая кривая [СО](ϕ)

Отображенный на рис.3 переходный процесс сопровождается увеличением удельного выброса СО примерно в 3 раза по сравнению с исходным и конечным установившимися режимами. Его продолжительность зависит от инерционности транспортного средства и динамических свойств трансмиссии. Разгон двигателя осуществляется за 20–30 оборотов коленвала, что соответствует примерно двум секундам ускоренного движения городского автобуса. Важно отметить, что в городском ездовом цикле переходные режимы ДВС часто доминируют [1, 2].

Кроме того, реалистичные модели должны учитывать число цилиндров и тактность двигателя, весь спектр выбрасываемых токсичных веществ (ТВ) и различия их индивидуальной ядовитости. В результате усложняются кинетические кривые как отдельных ТВ, так и суммарной токсичности заряда [1, 2]. Отметим, что динамика интегральной токсичности ТВС и ОГ немонотонна.

Рассчитанная согласно описанной модели, внутрицилиндровая кинетика углеводородов, альдегидов и NO, в т.ч. их содержание в ОГ тепловозного дизеля 10Д100 показаны на рис.4.

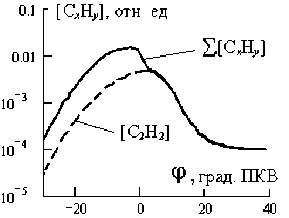
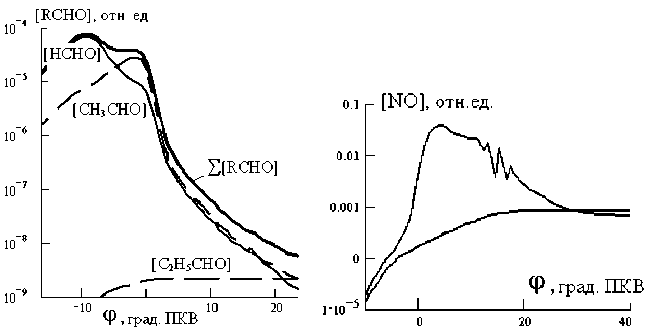
а)                                             б)                                                в)

Рис.4. Кинетика в среднеоборотных дизелях на примере тепловозного дизеля 10Д100: а – углеводородов; б – альдегидов; в – оксида азота

Условия расчетов соответствуют номинальной мощности для углеводородов и альдегидов, а для NO – номинальной (экстремальная кривая) и половинной (монотонная кривая) мощности. Содержание токсичных компонентов в ТВС дается в мольных долях.

По завершении фазы активного горения основным углеводородом в ОГ является ацетилен (рис.4,а). Это объясняется наибольшей прочностью С ≡ С связи ацетилена среди углеродуглеродных связей в моторных топливах. На этапе активного горения, однако, основным углеводородом в заряде является этилен: его доминирование объясняется тем, что С 1 -углеводороды окисляются существенно быстрее, чем С 2 -улеводороды, а С 3 -углеводороды, наоборот, заметно медленней. В результате С 1 -углеводороды сгорают практически мгновенно, а С 3 -углеводороды в течение характерного времени окисления С 2 -углеводородов успевают разложиться термически на С 1 - и С 2 -фрагменты.

Отметим, что рассмотренная ситуация отвечает условиям достаточно хорошего смесеобразования, при котором в выхлопе практически отсутствуют высшие углеводороды. Высокое качество смесеобразования в рассмотренном примере выражается также в незначительном содержании альдегидов в выхлопе (рис.4,б), что хорошо согласуется с современной теорией физикохимических процессов в ДВС [1, 2].

Экстремальный характер кинетической кривой NO на рис.4,в, которая соответствует номинальной мощности, означает, что при высокой теплонапряженности рабочего цикла ДВС кинетика внутрицилиндрового оксида азота двухстадийна. На первой или горячей стадии концентрация NO успевает отслеживать среднюю температуру заряда. Вторая стадия реализуется, когда средняя температура становится слишком низкой для протекания реакций гибели NO, и его содержание в ТВС «замораживается».

При частичных нагрузках средняя температура рабочего тела в течение всего цикла не достаточна для «запуска» реакций гибели NO, поэтому средняя концентрация окислов азота в рабочем теле монотонно увеличивается. В обоих случаях содержание NO в выхлопе близко к фактическому [1, 2]. Кроме того, рассчитанное соотношение NO-токсичности выхлопа при номинальной и половинной мощности получается вполне реалистичным.

Еще один практически важный результат компьютерных экспериментов с моделями состоит в выявлении сравнительно компактного и универсального химического механизма горения нефтяного моторного топлива в современных поршневых ДВС, что исключительно важно для технических приложений.

Авторы, воспользовавшись разработанными ранее технологиями и средствами [10], выявили элементарные реакции, определяющие химизм рабочего процесса поршневых ДВС. Полученная в результате оптимизированная схема превращений включает 70 реакций между 35 компонентами и пригодна как химический модуль перспективных моделей внутрицилиндровой динамики ДВС.

Относительное отличие индикаторных (силовых, энергетических) характеристик, рассчитываемых по оптимизированной и полной схеме, не превышает 5 %. Отметим, что оптимизированная схема была получена путем объединения двух частично оптимизированных схем – для режима холостого хода и номинальной нагрузки. Существенно, что выделенные авторами ключевые реакции в большинстве своем признаны также определяющими горение нефтяного топлива в условиях жидкостных ракетных двигателей [11].

Выводы. Разработана динамическая модель внутрицилиндровых процессов поршневого ДВС, позволяющая рассчитывать как интегральные и мгновенные энергетические показатели, так и токсичность отработавших газов. Модель позволяет сконструировать минимальную кинетическую схему, адекватно отражающую динамические свойства современных поршневых двигателей. Указаны перспективные направления совершенствования разработки и возможности ее применения для техники и технологий, сопряженных с использованием химических энергоносителей на транспорте.