Информационное обеспечение вычислительного эксперимента по расчету градиента давления в стволе скважины

Сравнительный анализ методик расчета градиента давления, используемых для проектирования обработки месторождений, показывает, что в настоящее время для них нет универсального критерия классификации и оптимального выбора.

Стоит отметить и то, что существующие в настоящее время общепризнанные методы расчета характеристик многофазного потока в стволе скважины, используемые в России и в мире, разработаны зарубежными учеными. Некоторые из них эмпирические, в других, напротив, делаются попытки моделировать явления, лежащие в основе тех или иных процессов.

Все эти модели можно разделить на 3 класса:

Эмпирические корреляции (Данс и Росс (1963), Оркижевский (1967), Мукерджи и Брилл (1985));

Модели дрейфа (Хасан и Кабир (1988));

Механистические модели (Ансари и др. (1994), Занг (2001)). [2]

Стоит отметить также, что термин «механистические модели» не является строго обоснованным, он употребляется в специальной литературе для обозначения класса методов расчета, в основе которых лежат законы гидравлики и гидродинамики, выраженные системами дифференциальных уравнений.[1] В математическом моделировании для этого класса методов используют термин «рациональные модели». Далее автор все же придерживается терминологии принятой в статье.

Механистические модели характеризуются наилучшей сходимостью с экспериментальными и промысловыми данными, но их использование в практических приложениях зачастую бывает затруднительным в связи с требуемыми вычислительными затратами. Модели, основанные на подходе дрейфа, позволяют производить вычисления на порядок быстрее, но характеризуются большей ошибкой расчётов. В частности, для снарядного режима многофазного потока – расхождение расчетов с экспериментальными данными достигает 30%. [2]

Категория «А». Рассматривает многофазный поток без учета режимов потока и эффекта проскальзывания. Плотность смеси рассчитывается на основе газового фактора. То есть, делается допущение, что газ и жидкость движутся с одинаковой скоростью. Используется одна единственная корреляция для двухфазного коэффициента трения. Не выделяются различные режимы потока.

Категория «В». Учитывает эффект проскальзывания, не учитывает режимы потока. Требуется корреляция и для объемного содержания жидкости и для коэффициента трения. Поскольку газ и жидкость движутся с различной скоростью, необходимо предусмотреть метод прогнозирования того, какой объем трубы занят жидкой фазой на любом участке трубы. Для всех режимов потока используются одни и те же корреляции объемного содержания жидкости и коэффициента трения.

Категория «С». Учитывает эффект проскальзывания и режимы потока. Для прогнозирования объемного содержания жидкости и коэффициента трения необходимы не только корреляции, но и методы определения режима потока. Определив режим потока, можно подобрать корреляцию для прогнозирования объемного содержания.

Жизненно важно, чтобы специалист, занимающийся расчетами, связанными с многофазным потоком, знал об ограничениях и области применения того или иного метода. Широкий разброс параметров, встречающийся в добывающих скважинах, осложняет разработку методов для прогнозирования поведения многофазного потока. Так методы, которые работают для газоконденсатных скважин, не работают для нефтяных, а допущения верные для одних скважин совершенно не допустимы для других. Целью настоящей работы является сравнительный анализ существующих общепринятых методов расчета градиента давления в скважинах с помощью информационных технологий. [3]

Для анализа были взяты рациональная модель Ансари и эмпирическая корреляция Бегса и Брилла. Был проведен полный факторный эксперимент. Фрагмент данных изображен в табл. 1.

Фрагмент данных для полного факторного эксперимента.

Нас интересует влияние на перепад давления нескольких факторов: температура на устье и на забое скважины, дебит скважины, плотность нефти, плотность газа и газовый фактор. Фиксировались значения давления в стволе скважины на высотах 540, 1080, 1890 и на забое – 2700м. Нулевой уровень выделен цветом – это данные реальной скважины месторождения в Западной Сибири.

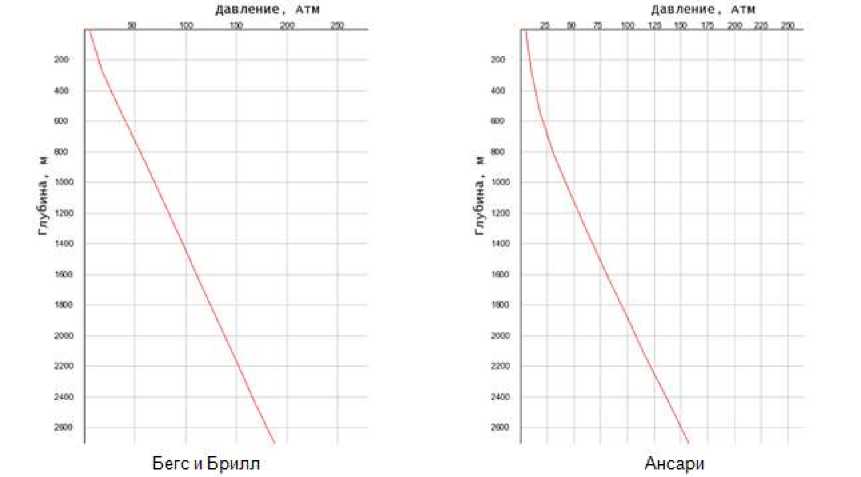
Рис. 1. Исходные данные по скважине.

Далее мы варьируем факторы в пределах допустимых значений, дабы проследить влияние каждого фактора в отдельности, а также в совокупности с другими факторами на градиент давления. Первичная обработка результатов вычислительного эксперимента представлена графически. Рис. 2 представляет собой зависимости давления от глубины скважины при варьировании дебита скважины и газового фактора для метода Бегса и Брилла (слева) и Ансари (справа).

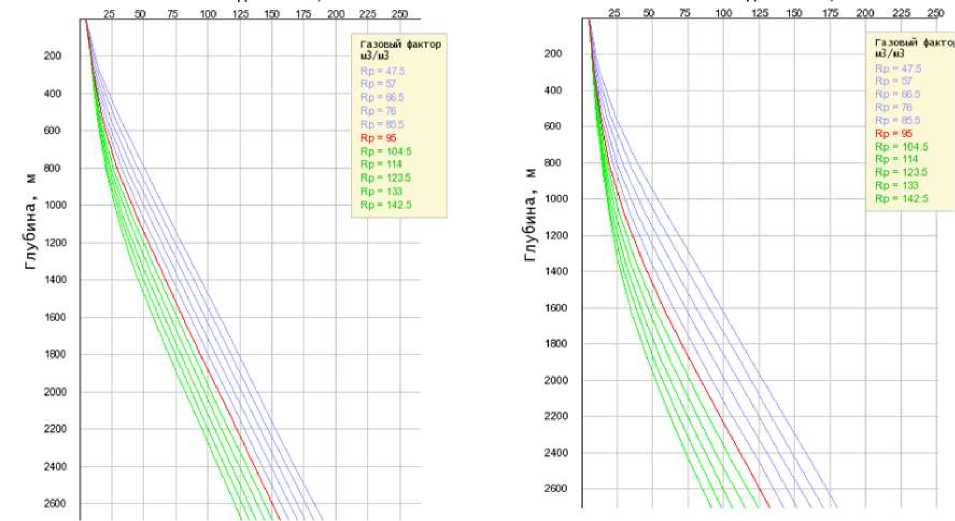
Рис. 2. Вариации газового фактора.

Проанализировав данные табл. 1 и графиков на рис. 1 и 2, а также на основе описательной статистики, было установлено, что наиболее значимыми функциями являются дебит скважины, температура на забое, плотность газа и газовый фактор, наименее значимыми – температура на устье и плотность нефти.

Все вычисления проводились с помощью онлайн вычислений сайта Центра технологий моделирования [4]. Представленная программа рассчитывает градиент давления в стволе скважины по корреляции Бегса и Брилла, и рациональной модели Ансари.