Информационный подход к описанию звукового сигнала

Следуя теории активного восприятия [1], введём понятие звукового сигнала. Звуковым сигналом называется множество М, каждый элемент которого в фиксированный момент времени t есть неотрицательная действительная функция действительного аргумента:

_М = Г /(t), ecnnt G Т С R,

[ 0 — в противном случае, определённая на конечном множестве точек замкнутого одномерного интервала Т, суммируемая: J^p / (t) dt < той квадратично интегрируемая: JtGp / (t)2 dt < то.

Разработка, оптимальных методов цифровой обработки звуковых сигналов невозможна, без создания подхода к описанию сигнала. Звуковой сигнал представляет собой физический процесс, принадлежащий окружающему миру, вследствие этого он обладает свойствами и законами окружающего мира. К таким свойствам относятся упорядоченность и структурированность. Условие упорядоченности обеспечивает существование бинарного отношения частичного порядка, типа.

(а 6 b) = {

а <  b — строгий порядок, а = b — тождество.

Условие структурированности, с учётом упорядоченности, указывает на наличие для любых пар элементов (а, b) существование границ - максимальной и минимальной. Учитывая, что о наблюдаемом звуковом сигнале в заданном интервале отсутствуют какие-либо априорные данные, последующая обработка, такого сигнала, выполняется в условиях априорной неопределённости. Рассматривая звуковой сигнал как системное образование, задача раскрытия априорной неопределённости сигнала заключается в выделении структурных элементов сигнала, и определении связей между ними.

1.    Предварительная обработка сигнала

Система, обработки данных (СОД) с точки зрения системного анализа, выполняет три этапа обработки данных (см. рис. 1): подготовку и анализ данных, принятие решения. Система, распознавания образов является одним из примеров СОД.

На этапе создания исходного описания в классических системах распознавания решается задача предварительной обработки анализируемого сигнала, которая заключается в фильтрации сигнала. Данную операцию можно описать уравнением Фредгольма первого рода:

9 (ж) = У ter

К (ж, t) J (t) dt,

где 9 (ж) - наблюдаемая функция, J (t) - неизвестная функция (априори неизвестное изменение во времени амплитуды регистрируемого сигнала на входе устройства), К (x,t) - ядро преобразования.

Фильтрация сигнала выполняется с целью компенсации помех, которые искажают сигнал в процессе его передачи от источника к приёмнику.

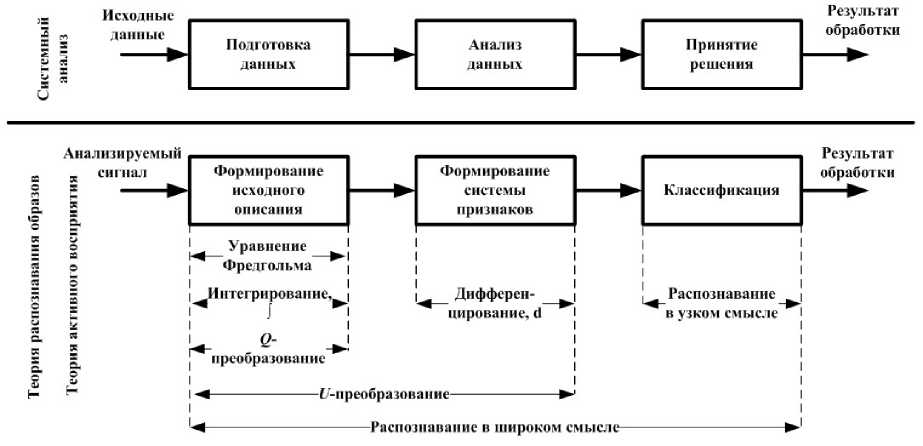
Рис. 1. Этапы обработки информации

Учитывая, что незначительные изменения в наблюдаемом сигнале J (t) могут привести к недопустимо большим изменениям в решении, результат, получаемый после выполнения фильтрации, в рамках использования уравнения Фредгольма является некорректным. Таким образом, сама задача предварительной обработки, описываемая с помощью уравнения Фредгольма, также некорректна [2]. Следовательно, основной задачей на шаге предварительной обработки является избавление от некорректности, возникающей в результате вычисления преобразования Фредгольма.

2.    [/-преобразование

Методам решения некорректных задач посвящено большое количество работ. К численным методам решения некорректных задач относятся методы подбора и методы регуляризации, к формализованным - метод Галёркина и проекционные методы [2]. Один из способов приведения некорректной задачи к корректной описан в Теории активного восприятия (ТАВ) [1].

В данной теории этап формирования исходного описания сигнала соответствует Q- преобразованию. Q-преобразование выполняется в соответствии с уравнением Фредгольма и в качестве ядра преобразования К (t, ж) использует единичную весовую матрицу. В результате уравнение Фредгольма приводится к следующему виду:

9 (ж) = j ter

J (t) dt.

Уравнение данного вида является корректным, вследствие того, что из него исключена операция дифференцирования, а операция интегрирования является корректной [3].

Применение операции интегрирования к сигналу f (t):

т (Т) = У tET

f (t) dt

позволяет получить представление о сигнале в целом:

• 1)    если результат интегрирования (т (Т)) отличен от нуля, то рассматриваемый сигнал содержит информацию и можно продолжить исследование структуры сигнала;

• 2)    если результат интегрирования равен нулю, дальнейший анализ сигнала не имеет смысла.

3.    Формирование описания сигнала

С позиций физики Q-преобразование выявляет массу в области определения, для которой f (t) - это плотность вещества. Таким образом, Q-преобразование за одно измерение позволяет получить об анализируемом сигнале один бит информации и выявить структурный элемент сигнала.

Поскольку все отсчёты сигнала находятся в отношении эквивалентности, то множество отсчётов можно разбить на любое число подобластей без пересечения этих областей между собой. Последовательное применение операции дихотомии и Q-преобразования к сигналу позволяет сгенерировать пирамидальную структуру (см. рис. 2).

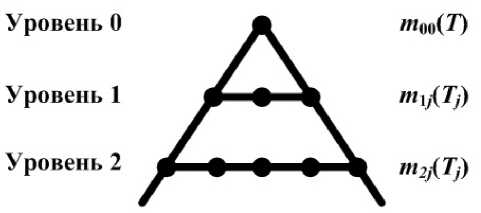
Рис. 2. Пирамида, описания сигнала.

Результатом формирования пирамидального описания сигнала является множество структурных точек {т^ }, г де г - уровень анализа, j - номер подобласти сигнала. Для выявления бинарных отношений (связей) на. множестве структурных элементов необходима, и достаточна, операция вычитания. Таким образом, в рамках теории активного восприятия звуковой сигнал рассматривается как системное образование. Для обнаружения системных элементов используется интегральное преобразование, а для выявления связей между элементами - пространственное дифференцирование. Результатом выявления дифференциальной структуры является спектральное описание сигнала. Преобразования интегрирования и дифференцирования образуют композицию, которая называется ^-преобразованием: U = d • R.

Рассмотрим задачу определения необходимого и достаточного числа, дихотомий наблюдаемого звукового сигнала, с учётом построенной пирамиды исходных описаний, начиная с её вершины (см. рис. 2):

• 1)    при нуле дихотомий вычисляется масса по всей области определения тоо (Т ), если она не равна нулю (тоо (Т ) = 0), то имеем достоверное событие наличия сигнала на интервале наблюдения;

• 2)    дихотомия интервала, пополам позволяет выполнить локализацию положения экстремума. на. анализируемом интервале относительно центра: слева, либо справа. Каждой половине интервала соответствует масса тц, ті2(см. рис. За) [4]. Отношение между этими массами имеет следующий вид: ц = тц — ті2- Рассмотрим возможные варианты значения ц:

• а)    ф = 0: сигнал симметричен относительно центра, следовательно, на данном уровне локализовать положение экстремума нельзя и следует перейти на следующий (более точный) уровень;

• б)    ф < 0: экстремум расположен слева от центра интервала;

• в)    ф > 0: экстремум расположен справа от центра интервала;

таким образом, дихотомия интервала пополам позволяет проверить гипотезу об однородности (симметрии) сигнала;

• 3)    дихотомия отрезка на четыре равных интервала (уточнение положения экстремума, см. рис. 36), поставим в соответствие каждому из интервалов массу: т₂₁, т₂₂, т₂з, т₂₄. Отношение между массами имеет следующий вид: ф1 = (т₂₂ + т₂з) — (т₂₁ + т₂₄) и Ф2 = (т₂₁ + т₂₃) — (т₂₂ + т₂₄). Анализ значений ф1 и ф₂ позволяет определить положение экстремума: в трёх случаях получаем, что на сигнале находилось два экстремума (т. е. один экстремум на нулевом уровне разделился на два экстремума на втором уровне), в одном случае (два шарика по центру) получаем, что для локализации экстремума требуется переместиться на уровень ниже (выполнить более тонкий анализ).

4.    Алгебра групп

Рис. 3. Дихотомия отрезка: а) пополам; б) па. четыре части

Таким образом, получаем четыре базисных одномерных фильтра-покрытия ( Fq, Fy Ғ₂, Ғ₃), которые позволяют выделить отношения между парой масс (см. рис. 4).

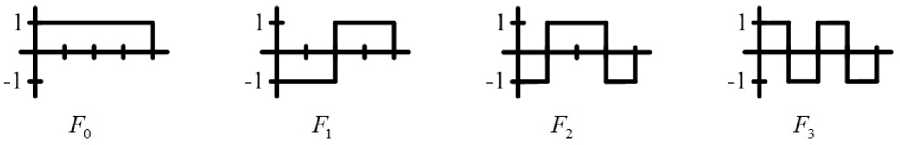
Рис. 4. Базисные функции

Исследования показали, что для целей анализа звукового сигнала необходимо использование 16 фильтров, которые можно построить по аналогии с четырьмя фильтрами. Результатом имеем систему базисных одномерных булевых функций, которая внешне похожа. на. систему базисных функций Уолша, системы Хармута. Специфика, использования данной системы заключается в том, что она. применяется после реализации (^-преобразования и сразу по всей области определения.

Теория активного восприятия не ограничивается только формированием спектрального представления сигнала. [1]. В ТАВ входит раздел «Алгебра, групп», посвящённый анализу зависимостей между спектральными коэффициентами разложения. Обнаруженные зависимости допускают своё использование на этапах принятия решения и понимания анализируемого звукового сигнала.

Примем для множества фильтров {ҒД, что (+1 ^ 1) и (—1 ^ 0). Получим множество бинарных операторов {РД. Для этих операторов допустимы теоретико-множественные операции объединения (сложения) и пересечения (умножения). Результатом имеем алгебру - А у = ({РД : +, х) [1]. В алгебре А у существуют алгебраические группы:

• 1)    Pm - группы на трёх элементах (названы полными), образованы на тройках операторов (V), Vj, V_k), для которых справедливы соотношения: V) + Vj + V_k = е1 - единица; VVjV_k - образ, формируемый с помощью операции умножения и описание группы Pm,

• 2)    P_s) - группы на четырёх элементах (названы замкнутыми), образованы на четвёрке операторов (V), Vj, V_n, Vn), где (V), Vj, V_k) G P^, (V_n, Vm, V_k) G P_nj, с описанием VVj + V_nV_m и единицей - V) + Vj + V_n + V_m = e1.

5.    Идентификация звукового сигнала 5.1.    Формирование отпечатка сигнала

Алгебра групп используется для формирования описания звукового сигнала. С помощью замкнутых и полных групп выполняется спектрально-корреляционный анализ. Полные группы позволяют выявить корреляционные связи между операторами. Замкнутые - корреляционные связи между полными группами.

Количество музыкальных композиций, хранящихся в настоящее время в сети Интернет, велико (например, сервис Яндекс.Музыка хранит около пяти миллионов записей, сервис Shazam - пять миллиардов). Очевидно, что в такой ситуации актуальна задача быстрого и точного поиска по имеющимся музыкальным записям. Рассмотрим алгоритмы, предлагаемые для формирования цифрового отпечатка звукового сигнала и для поиска сигнала в базе данных.

Пусть f (t) - звуковой сигнал, наблюдаемый на конечном отрезке времени. Результат применения ^-преобразования к сигналу f - многоуровневое спектральное представление D = {d ij }, г = 1,K, j G 1,М), где К - число уровней разложения, М ) - количество сегментов сигнала на i-м уровне разложения, d )j - спектр, включающий L спектральных коэффициентов (число используемых фильтров), d )j {к} - к-й спектральный коэффициент (к = 1,L), f )j - сегмент сигнала f, по которому вычислен спектр d )j.

Рассмотрим алгоритм формирования отпечатка звукового сигнала:

• 1)    построение на основе ^-преобразования спектрального представления D сигнала f (при построении разложения сегменты f )j не перекрываются); в предлагаемом алгоритме вычисляется только один уровень ^-преобразования, в связи с этим значение индекса i для краткости записи не приводится;

• 2)    формирование огрубленного представления С = {c j } спектрального представления D = {d j } (степень огрубления - параметр к) [5]:

• 3)    выбор ключевых сегментов сигнала f:

V j G VM^

V t G 1, L, если |cj (t) | 6 к inii |cj (t)| > l (к < I), to

К j .data [j] = f j ;

Ключевой сегмент соответствует участку сигнала, на котором максимален отклик небольшого количества операторов (одного-двух). Это означает, что сегмент сигнала подходит под образ операторов, давших максимальные отклики;

• 4)    вычисление по каждому ключевому сегменту замкнутых групп и отбор из полученного набора первых N по массе групп:

Vj G ГКі ,

Wj.shift [j] = Kj [j] .shift, где \К j| - мощность множества К j, GRP [•] - оператор, который вычисляет замкнутые группы по сегменту сигнала, max [•] (min[*]) - оператор для поиска среди групп набора, Wj.groups [j] - группы с максимальной (минимальной) массой, j - номер ключевого сегмента, Wj - предварительное описание сигнала f, Wj.diff [j] - разница между максимальным и минимальным значением масс групп в Wj.groups [j], Wj.shift [j] - смещение j-го ключевого сегмента относительно начала сигнала;

• 5)    отбор устойчивых сегментов сигнала (эксперименты показали, что устойчивость сегмента сигнала к искажениям тем лучше, чем больше разница между максимальной и минимальной массами групп, входящих в описание сигнала):

5.2.    Поиск отрывка звукового сигнала в базе данных

V j G 17|Mji, если Mj .diff [j] > T,

M j .groups [fc] = W j .groups [j ] ;

fc = fc + 1, где Mj - описание сигнала, f. содержащее только устойчивые сегменты сигнала. T - значение порога.

Допустим, с помощью алгоритма, приведённого в пункте 5.1, сформирована база данных описаний звуковых сигналов. Рассмотрим алгоритм поиска, звукового сигнала, в базе данных:

• 1)    формирование отпечатка M _s искомого сигнала s (в отличие от алгоритма, описанного в пункте 5.1, шаг отбора, устойчивых сегментов сигнала, пропускается, сегменты, на. которые разбивается сигнал, перекрываются);

• 2)    поиск отпечатка M _s в базе данных заключается в сравнении пар элементов в описании i-ro сигнала базы данных и сигнала s, которые находятся на одинаковых расстояниях: в случае, если такие пары найдены, вычисляется расстояние между их описаниями:

• 3)    если di > T и T - порог, то в массив R сохраняется абсолютное значение расстояния между элементами M j,i .groups [fc] и M _s .groups [m]:

R [p] = \M f,i .shift [fc] - l\ .

После окончания сравнения описаний i-го из базы данных и искомого сигнала s по массиву R формируется гистограмма. Гистограмма сигнала, который включает искомый сигнал s, будет иметь ярко выраженный максимум [6].

Заключение

В работе рассматривается информационный подход к описанию звукового сигнала, вводится понятие звукового сигнала, как системного образования, описывается метод обработки сигнала, в условиях априорной неопределённости. Данный метод заключается в последовательном применении к анализируемому сигналу операций интегрирования и дифференцирования, что позволяет выделить структурные элементы сигнала, и определить связи между ними. Достоинствами рассматриваемого метода, формирования описания сигнала.

является низкая вычислительная сложность и простота реализации. В качестве примера описанного подхода к обработке звуковых сигналов рассматривается решение задачи идентификации звуковых записей.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках договора № 02.G25.31.0061 от 12 февраля 2013 года (в соответствии с Постановлением Правительства Российской Федерации от 9 апреля 2010 г. № 218).

Работа, отраженная в данной статье, признана лучшей на Всероссийском конкурсе научных и инновационных проектов студентов, аспирантов и молодых ученых (МФТИ-2012).