Information Technologies for Decision Support in Industry-Specific Geographic Information Systems based on Swarm Intelligence

Nowadays, universal geographic information technologies (for example, ArcGIS and Quantum GIS) are used for the ever-increasing volumes of spatially distributed input data of various nature, which are often characterized by uncertainty and incompleteness. They require complex refinement to support decision making when solving numerous industry-specific tasks, which are described by their own criteria and constraints. Reasonable choice of decision-making methods in industry-specific geographic information systems (GIS) has a significant impact on their speed, effectiveness, and the ability to meet the requirements of practice. The basic methods and technologies for decisionmaking are segmentation, identification, clustering, classification of spatial data, as well as the selection of suboptimal spatial trajectories and routing [1]. At the same time, one of the main factors affecting the quality of these methods is optimization methods used in these basic procedures. This is because objective functions, as a rule, are multidimensional, multimodal, and have a random component, since decision support systems (DSS) in industryspecific GIS work under conditions of uncertainty when processing large input data that have a variable nature, distributed sources, and heterogeneous semantic component. Under such conditions, the best result is obtained using metaheuristic methods of swarm intelligence.

Swarm intelligence methods (SIM), compared to classical methods under conditions of uncertainty, can find a suboptimal solution more effectively when solving high-dimensional, multimodal, and weakly formalized problems, and ensure a high probability of localization of the global extremum of the objective function [2]. However, lack of a formalized approach to determining the necessary SIM and lack of tools for setting a large number of their free parameters inhibits the use of SIM for the creation of integrated geoinformation technologies to support decisionmaking for a number of industry-specific tasks with their own criteria and constraints considering the set of input geospatial data and their visualization method [3, 4].

Thus, when creating industry-specific GIS on the basis of existing geoinformation technologies, a significant problem arises, which is due to modern requirements for supporting informed decision-making in solving industryspecific problems that are associated with obtaining, analyzing, modeling and visualizing spatial and attributive digital data about the location and features of territorially distributed objects as well as the limitation or lack of existing implementation support for the creation of appropriate integrated information technologies using SIM [5, 6].

To solve this problem, we propose using metaheuristic optimization algorithms, namely swarm algorithms, since they allow solving high-dimensional problems with weakly formalized data and multimodal objective functions; developing a method of choosing swarm methods for solving specific applied tasks; on the basis of the chosen optimization methods, developing methods, algorithms, and basic information technologies for data processing in DSS of industry-specific GIS.

2.    Related Works

Article [7] proposes a method of forming territorial communities using bat and gray wolf algorithms. A mathematical model of the community formation method is developed. The effectiveness of the method is investigated the effectiveness of the method on the example of the formation of territorial communities in the Chernivtsi region (Ukraine). The proposed method is tested on the basis of GIS technologies and statistical data.

Article [8] proposes an approach to the formation of territorial communities using algorithms of collective intelligence. The approved methodology for the formation of communities is investigated, and a mathematical model. The stochastic algorithms of an ant colony and a flock of birds are adapted to to solve a multi-criteria optimization problem. A study of the proposed approach was studied.

The studied materials made it possible to substantiate the need to develop a method for selecting swarm optimization algorithms and using swarm intelligence methods to solve a certain class of optimization problems in sectoral geographic information systems, taking into account the stationarity of such systems, and to study the classes of swarm algorithms.

Summarizing the above, the urgent problem is to improve the quality and/or efficiency of decision support based on swarm intelligence for industry geographic information systems by creating appropriate models, methods, and information technologies.

The aim and tasks of the research. The aim of this paper is to develop and research information technologies for decision support for industry-specific geographic information systems based on swarm intelligence to improve the quality and/or efficiency of processing.

To achieve this aim, the following tasks need to be completed:

Development of a conceptual decision support model for geographic information systems and a decision support method based on it;

Development of a method for choosing swarm optimization methods to work as part of the DSS of industryspecific GIS.

3.    Material and Methods

Since it is appropriate to use SIM for industry-specific GIS, we have developed a conceptual model of SI, which is set by the expression:

MSI =< S, M, A, P, 1,0 >

where S - a set of agents (individuals), i.e. a swarm (population); M - an object for exchanging experience between agents, most often a matrix (can be a vector), to which all agents Ag of the swarm (population) have access according to certain rules A (P); A (Р) - rules of creation, behaviour, and modification of agents; P - parameters (heuristic coefficients) that are used in the rules A. P parameters can be static and dynamic; 1 1 - system input, to which the objective function is fed, f t - the preference function (fitness function) is used to describe and compare the quality of decisions, constraints, I _oc - input for feedback; 0 = {0 1 ,0_ос }, 0 1 - output (best problem solution found), 0_ос - output for feedback.

Each agent can be presented in the following form:

Ag = ⁽TAg, OAg)

where TAg - type of agent. The place of the agent is defined by its quality or type (some weight function), OAg -neighbourhood of the individual. During algorithm functioning, the neighbourhood of the individual may change (be dynamic) or remain unchanged (be static).

Each swarm S is set by the following characteristics:

S = (TS, R, SA)

where TS – swarm type (static, dynamic). If during the merging of swarms new individuals appear, the swarm is considered variable, if previous individuals remain, the swarm is static. R - swarm size, SA - population merging metrics (distance, weight, speed, cognitive behavior, social behavior, etc.) (PMM), may be variable or constant.

It should be noted that rules for organizing the merging of a swarm are determined by a specific type of algorithm and are set as multiple actions:

A = (multiple actions, СА)

where СА - complexity of algorithm. In terms of complexity, algorithms can be simple (the iteration contains one process) and complex (the iteration contains several processes).

Table 1 gives a generalized description of parameters of existing SIM [8-14].

These parameters’ values enable us to choose the method of swarm intelligence depending on the problem class.

Table 1. Generalized description of parameters of existing SIM

	Features	Parameters P (static, dynamic)	Population merging metrics PMM (constant, variable)	Agent Ag (quality, type)	Swarm S (static, dynamic)	Agent neighbourhood O Ag (static, dynamic)	Algorithm complexity (simple, complex) СА
	Algorithm
1	Ant	Static	Variable	Quality	Static	Dynamic	Simple
2	Bee	Static	Constant	Type	Static	Dynamic	Simple
3	Bat	Static	Constant	Type	Static	Dynamic	Simple
4	Shoal of fish	Dynamic	Constant	Quality	Static	Dynamic	Simple
5	Genetic algorithm	Dynamic	Variable	Quality	Dynamic	Dynamic	Complex
6	Swarm of particles	Static	Constant	Quality	Dynamic	Dynamic	Simple
7	Harmony search	Static	Constant	Quality	Static	Static	Complex
8	Fireflies	Static	Constant	Quality	Dynamic	Dynamic	Simple
9	Grey woolves	Dynamic	Constant	Type	Static	Dynamic	Simple
10	Stochastic Diffusion Search	Static	Variable	Quality	Dynamic	Static	Simple
11	Variable Mesh Optimization	Dynamic	Constant	Quality	Static	Static	Complex
12	Shuffled Frog Leaping	Dynamic	Constant	Quality	Dynamic	Dynamic	Simple
13	Migrating Birds Optimization	Static	Constant	Quality	Dynamic	Dynamic	Simple
14	Differential Evolution	Static	Constant	Quality	Static	Static	Simple
15	Bacterial Search	Dynamic	Variable	Quality	Dynamic	Static	Simple
16	Artificial Immune System	Static	Constant	Quality	Static	Static	Simple

Let us consider the method of choosing swarm optimization algorithms and the use of swarm intelligence methods to solve a certain class of optimization tasks for an industry-specific GIS taking into account the stationarity characteristic of the GIS.

4.    Method of Choosing Swarm Algorithms

The method of choosing swarm optimization algorithms consists of the following stages:

Stage 1. Classification of industry-specific GIS by stationarity characteristic.

Stage 2. Conceptual information modeling and analysis of the chosen industry-specific GIS, the purpose of which is to determine the type of objective functions.

Stage 3. Development of a decision support method for the construction of an industry-specific GIS.

Stage 4. Choice of a set of swarm optimization methods based on ontological analysis of existing analogues when solving similar problems.

Stage 5. Preliminary analysis of optimization methods using test objective functions. The result of the analysis is one or more optimization methods suitable for solving the given problem.

Stage 6. If none of the considered swarm intelligence methods meets the requirements of practice, a method of combined application of two swarm optimization algorithms is developed.

Stage 7. Adjustment of free parameters of swarm intelligence methods to the requirements of a specific applied problem.

Stage 8. The final choice of a set of optimization methods in a GIS as a whole and its individual procedures and its testing in specific applied problems.

Let us consider the aforesaid stages in detail.

Stage 1.

Let us analyse the existing classification systems (Fig. 1.). It is shown that it is important to take into account the stationarity characteristic of the industry-specific GIS input data when developing new decision support information technologies for the GIS. A classification of tasks solved in an industry-specific GIS (stationary, quasi-stationary and dynamic) is proposed, taking into account the stationarity characteristic, which has made it possible to develop a method of justified choice of the method for solving optimization problems in these systems.

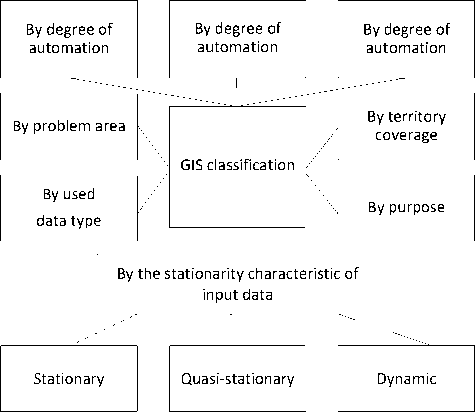
Fig. 1. Industry-specific GIS classification method.

It is proposed to regard the industry-specific GIS in which parameters of the objective functions and constraints do not change as stationary industry-specific GIS. Quasi-stationary industry-specific GIS are aimed at solving tasks in which the parameters of the objective functions and constraints (including time) practically do not change during the execution of the task. Dynamic industry-specific GIS solve tasks in which it is necessary to take into account the changing situation (including during the operation of the industry-specific GIS). In contrast to quasi-stationary industryspecific GIS with a time limit, in a dynamic industry-specific GIS with a time limit, the conditions of the problem can change during its solution. The introduction of this classification feature allows choosing the optimization criterion reasonably for both the industry-specific GIS as a whole and its individual procedures.

In the vast majority of cases, the central component of an industry-specific GIS is DSS. We have analysed the models and methods of data processing, on which decision-making in existing industry-specific GIS is based. One of the basic tasks that define the quality and efficiency of decision-making is the clustering and classification of objects and the determination of suboptimal trajectories of object movement.

It is shown that solving these problems requires a global optimization procedure. It is proved that since data in industry-specific GIS are a priori characterized by uncertainty and incompleteness, the objective functions are usually characterized by multimodality, high dimensionality, complex topology of the range of permissible values, etc. It was established that the gradient and subgradient optimization methods used in existing industry-specific GIS do not have the required accuracy and speed under the specified conditions. It is optimization methods based on swarm intelligence (SI) that meet the necessary requirements.

Stage 2.

In order to unify the presentation of data in industry geoinformation systems (geodata), ensure the necessary accuracy of obtaining spatially distributed data, and ensure the completeness of attributive data about industry-specific GIS objects, an information model of geoscience was developed:

MGD =< MGD_S, MGD_a, MD >

where MGD_S - a model of spatial (coordinate) data containing information about the spatial position of industryspecific GIS objects and describing their geometry, MGD_a - an attributive data model that describes the qualitative and quantitative properties of spatial objects of industry-specific GIS, MD - metadata containing information about the source data, the methods, and the time of obtaining geodata about objects.

It is proposed to represent the industry-specific GIS spatial data model as a tuple:

MGDS =< TP, FP, TPro, LoS >

where T_P = ]2D]raster, vector_nontop, vector_top],3D{Grid, TIN}] - type of representation of 2D -objects, raster -raster representation using characteristics: resolution, value, orientation, zone, position, etc; vector_nontop - vector representation in the form of a set of coordinates of linear segments; vector_top - vector representation in the form of a set of coordinates of linear segments with the additional setting of such characteristics as: connectivity, intersection, proximity; Grid - representation of 3D-objects using regular grids; TIN - representation of 3D-objects using adjacent, non-intersecting triangles; F_P = {isolines,isoconturs, gradient} - form of representation of 3D -objects using isolines, isocontours, and gradient fill. The LoS parameter specifies a library that contains sets of standard conventions, symbols, and accepted notations for displaying industry-specific GIS spatial objects.

Taking into account the possibility of spreading existing models of knowledge representation, it is proposed to present the attribute data of industry-specific GIS using the following model:

MGDa

=I

T_F, E, S i , S₂, S₃

T r , E, R, T_s, E,{R}, G,

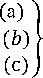
where T_R , T_s , T_F - relational, semantic, and frame models of knowledge representation, (а) - sets of objects E, relations between them R, and their attributes A, if the relational model T_R is chosen for the representation of attribute data, (b) -мa set of relationship types {R}, such as hierarchical, causal, functional, etc., and G – a mapping that takes into account specific relationships from the set of relationship types {R} between objects E, if semantic model T_s is chosen, (c) -sets of slots S 1 , S₂, S₃, which contain the declarative and procedural semantics of frames and ensure their connections if frame model T_F is chosen to represent attribute data.

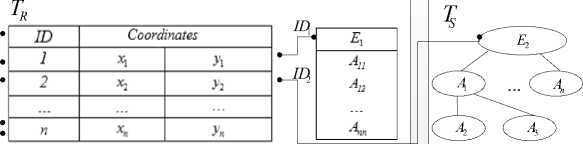
To ensure the integrity of geodata, it is proposed to link their spatial and attributive components with the help of identifiers (ID) of objects (Fig. 2).

MGD S

MGD A

T

F

ID n

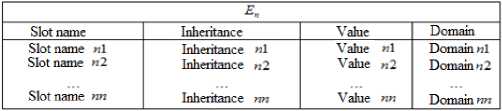
Fig. 2. Georelational relationship of spatial and attributive components of geoinformation data considering the model of representation of the attributive component.

Thus, the formalized combination of spatial and attributive components, which takes into account the relational, semantic and frame models of knowledge representation of the attributive component, made it possible to develop knowledge base technologies.

Taking into account the features of typical tasks in an industry-specific GIS, a conceptual model of decision support is proposed, which takes into account and divides the tasks solved by industry-specific GIS into different levels:

In the expression (8) W₀ - the first-level task that is aimed at solving the general aim of creating an industryspecific GIS and affects the solution of second-level tasks that are solved by the industry-specific GIS, W 1 , W₂,..., W_n. R 1 , R₂,..., R_n - a set of received solutions for the tasks set.

It is shown that when determining a task from the set of tasks of the second level Wi, it is necessary to take into account not only the task type, but also its proposed stationarity characteristic (or the dynamics of change) Т (T_R , T_s , T_F ) in the industry-specific GIS according to the classification proposed in the first section.

The rational solution of the second-level task considering the geodata model (5) and the dynamics of change in geodata Т (T_R , T_s , T_F ) depends on a number of factors and can be described using the following:

X r =< W o , T, MGD_S, MGD_a, MD | W , (a , , & , ^ , X , ), M , (p), f , k , >, i = 1,4              (9)

where a , - initial operational data for decision-making depending on the task, & - constraints; X , = (X^,..., X , _m) - a set of alternative solutions for each second-level task, and X_R EX , - rational decision; M , (p) E М - SIM for solving the W , task from the SIM base, f - the preference function (fitness function) is used for the description and comparative assessment of the quality of decisions based on the advantages of the decision maker (DM), ki – the criterion for choosing a rational decision formulated by the DM, n - number of tasks.

Therefore, considering (9), the task of supporting decision-making in industry-specific GIS is formulated as follows (Fig. 3): under the given conditions α and β, considering the stationarity characteristic and using the reasonably chosen method M , , find such a decision X_R E X , , which the DM choses from the set {X , }, which is pre-ordered according to the preference function f, while taking into account the criterion k.

On the basis of the proposed information model of geoscience presentation and the conceptual model of decision support in industry-specific GIS, a method of decision support during the construction of a industry geoinformation system was developed. The method is implemented as follows (Fig. 3):

Step 1. Formation of the first-level task W_o (aim).

Step 2. According to W_o , a geoscience database is created based on spatial and attributive data about the objects of the industry and considering the information model (1).

Step 3. On the basis of W_o and data from the geoscience database, the set of second-level tasks W 1 , W₂,..., W_n is defined. The following sequence of steps is performed for each task.

Step 4. For each task W , , additional initial information is defined according to the conceptual model (8).

Step 5. To solve the task W , , its solution scenario is selected reasonably on the basis of SI.

Step 6. The set of alternative decision options is formed {X , }.

Step 7. The choice of the reasonable (acceptable) decision X_R is made according to the choice criterion k , formulated by the DM.

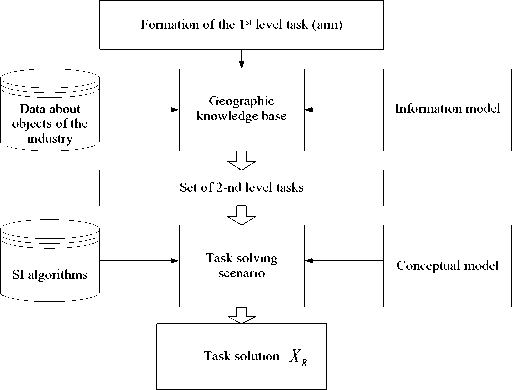
Fig. 3. Generalized structure of DSS in industry-specific GIS.

The aforesaid procedures use optimization methods both at the stage of development and in the course of functioning.

Stage 3.

The analysis of DSS allowed identifying the following procedures, methods, and basic IT solutions: segmentation, identification, clustering, classification, and the construction of suboptimal trajectories. A specific DSS structure is determined according to the purpose of processing depending on the applied task. Then its system and/or informational analysis is carried out. The result of the analysis is the criteria of quality and efficiency of the system as a whole and of its individual procedures, the impact of individual procedures on the DSS as a whole, and the method of quantitative assessment of the decisions made. In this work, to quantify the decisions made, it is proposed to use statistical estimates of the probability of each of the possible decisions obtained at the classifier training stage. The results of the system analysis make it possible to define the types of objective functions that determine the quality and efficiency of the basic procedures by means of conceptual and informational modelling at the stage of preliminary research.

We receive the following steps of the decision-making method:

Step 1. Conceptual and informational modelling of DSS. Development of DSS structure.

Step 2. Conceptual and informational analysis of DSS. Selection of criteria for quality and effectiveness of decision-making procedures and the overall DSS.

Step 3. Assessment of the influence of indicators of individual procedures on the characteristics of DSS.

Step 4. Selection of the type of test functions of procedures.

Step 5. Optimization of decision forming procedures.

Step 6. Formation of the educational sample.

Step 7. Classifier training and statistical evaluation of the probability of each of the possible decisions Х 1 ... X_n.

Step 8. Testing and direct transition to the DSS operating mode.

Stage 4.

For this stage, we have developed an ontology based on the analysis of existing analogues for solving similar tasks [15, 16]. An example of a fragment of a knowledge base (ontology) is shown in Fig. 4. The main entities of such an ontology are the task class (task formulation, parametricity), the set of the most popular swarm algorithms and their features.

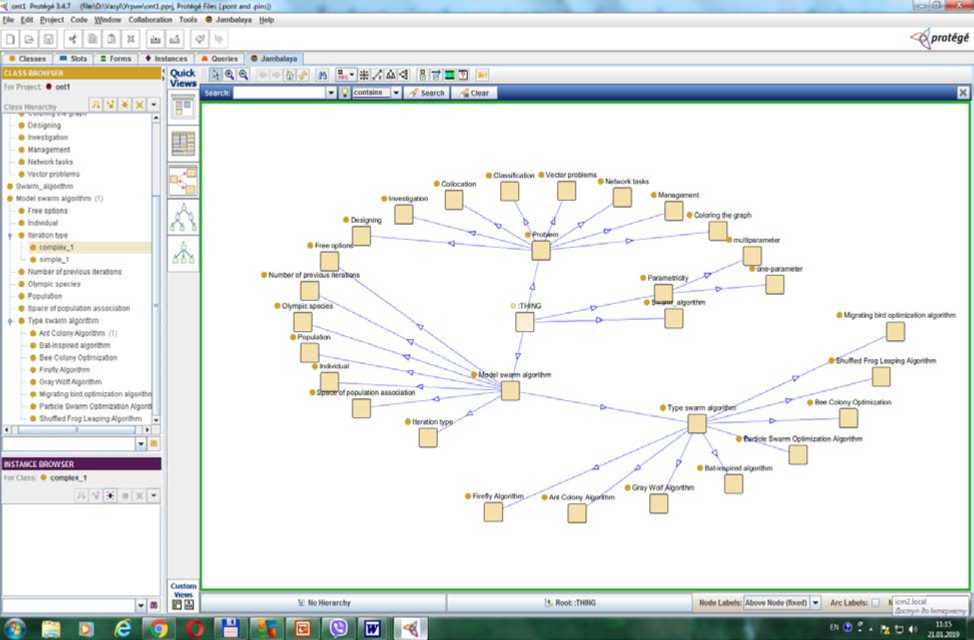
Fig. 4. An example of a fragment of a knowledge base (ontology) for choosing a SIM.

It is proposed to use a method of setting up swarm intelligence methods that allows formalizing the choice of free parameters and rules of organizing a union of populations.

The result of this stage is a set of swarm optimization methods based on the ontological analysis of existing analogues used in solving similar tasks [17-25].

At the fifth stage, a preliminary analysis of optimization methods was carried out using test objective functions. For a reasoned choice of SIM, in accordance with the stationarity characteristic of the tasks, it is proposed to do modelling on the main test functions. The result of the analysis is one or more optimization methods that can be used to solve the given task.

At the seventh stage, free parameters of swarm intelligence methods are adjusted to the requirements of a specific applied task. This allowed forming a base of SI methods for formalizing the selection of the SIM and adjusting its parameters to the task solved by the knowledge base according to the ontological approach.

The method is implemented as follows:

• 1.    The population is coded.

• 2.    Rules А and free parameters Р are set, which were obtained from the knowledge base regarding the choice of SI method for population processing. There are different SI rules and methods, depending on which the choice of a specific option can affect the speed and quality of the obtained decision. If free parameters of one SI do not allow obtaining alternative solutions, a combination of SI methods is used.

• 3.    Initialization of the population S. The population consists of a set of agents Ag. At initialization, each agent is placed randomly.

• 4.    Testing the algorithm for a different set of rules A and free parameters S.

• 5.    Considering the obtained best decisions, free parameters are stored in the form of results.

5.    Computer Experiment

At each step, the fitness function f is calculated for each population.

A new information technology has been developed on the basis of the proposed knowledge base and the methods of formalized selection of SIM and its parameters depending on the class of the task solved by the industry-specific GIS.

At the eighth stage, the final choice of the set of optimization methods in industry-specific GIS and its individual procedures is made and its testing is performed in specific applied tasks.

As a result of analysis, representatives of the main classes of test functions were selected for further study of the speed of convergence of swarm optimization methods. These test functions should allow investigating the speed of convergence of swarm metaheuristic optimization methods with a noisy objective function surface, a multimodal objective function with a false global extremum, an objective function with a ravine-type surface.

For representatives of these classes of model test functions, the speed of convergence of metaheuristic swarm methods was investigated. The research was carried out using the Rosenbrock function, which models a ravine-type surface, the unimodal de Jong function 1 with the addition of a noise component, and the Schwefel function, which models the surface of the objective function with a false global extremum.

Rosenbrock's function at work f 1 (x) = 100(x₂ — x 2 ) + (1 — x 1 ) 2 . In this function, at x E (-2.048; 2.048) the global minimum f 1 (x) = 0 at the values x 1 = 1, x₂ = 1. The de Jong function 1 f₃ (x) = x² was investigated at x E (—40; 40) with the addition of an obstacle. The obstacle was distributed according to the normal law with zero mean and standard deviation 400, the maximum value of the function was f₃ (x) = 1600. The Schwefel function f₂(x) = 418,9829 + (—x X sin^\x\')( with a false global minimum). In this function, at x E (—500; 500) the global minimum f₂ (x) = 0 at x = 420.9829. During the research, the starting point was chosen randomly.

The results of the convergence speed studies took into account the reduction of the error of finding the extremum of the objective function on iterations 50 and 100, respectively, for the Rosenbrock f 1 , Schwefel f₂, and de Jong f₃ test functions. The results of this assessment of the average speed of convergence for 20 runs of the corresponding algorithms are shown in Table 2.

Table 2. Results of investigating the convergence speed for the Rosenbrock f_, Schwefel f₂, and de Jong f 3 test functions

Method name	f l		f 2		f 2
	Iteration number		Iteration number		Iteration number
	50	100	50	100	50		100
Ant colony	10 °	10-1	5 X 10-1	4 X 10-1	2 X 100	8 X 10-1
Grey wolves	10-1	10-1	4 X 10-1	3 X 10-1	10-1	10-1
Bee colony	10-1	10-1	4 X 10-1	2 X 10-1	10-1	10-1
Particle swarm	10-1	2 X 10-1	3 X 10-1	2 X 10-2	2 X 10-1	3 X 10-3
Frogs	5 X 10-1	6 X 10-2	3 X 10-1	2 X 10-2	10-2	10-4

The results of investigating the error of finding the extremum coordinate for 20 runs of the corresponding algorithms using the above test functions are shown in Table 3. At the same time, ave is the average value of the error in determining the extremum coordinate, and std is the root mean square deviation of the estimates.

As a result of the research, it was found that in a number of applied programs (for example, in dynamic industryspecific GIS), with tasks that require operational conclusions of the DSS under rapidly changing conditions, increased speed is necessary. Therefore, combined swarm methods of metaheuristic optimization were investigated. Such methods, as research has shown, are characterized by higher speed with a sufficient error of finding the extremum for the specified applied tasks (see Table 4).

Table 3. Results of investigating the error of finding the extremum coordinate for 20 runs of the corresponding algorithms using test functions

Method name	A		A		A
	ave	std	ave	std	ave	std
Ant colony	10 °	10-1	5 x 102	7 x 101	6 x 10-10	8 x 10-5
Grey wolves	10 °	10-1	4 x 102	3 x 101	10-1	10-1
Bee colony	10 °	10-1	4 x 102	2 x 101	10-1	10-1
Particle swarm	10 °	2 x 10-1	5,2 x 101	2 x 101	2 x 10-1	3 x 10-3
Frogs	10 °	6 x 10-2	4,9 x 101	2 x 101	10-2	10-4

Table 4. Results of investigating of the convergence speed of combined swarm methods of test functions

Combined method name	f 1		/ 2		/ 3
	Iteration number		Iteration number		Iteration number
	50	100	50	100	50	100
Ant colony + flock of birds	10 °	10-1	5 x 10-1	4 x 10-1	2 x 10 °	8 x 10-1
Grey wolves + bats	10-1	10-1	4 x 10-1	3 x 10-1	10-1	10-1
Artificial immune system + bacterial search	10-2	10-3	4 x 10-2	2 x 10-3	2 x 10-2	2 x 10-4
Leaping frogs + particle swarm	10-2	2 x 10-3	3 x 10-1	2 x 10-2	2 x 10-1	3 x 10-3

Exactness was estimated by norm mean square deviation on the difference between the known and the calculated sub-optimal solution of the problem. Authors plan to develop a procedure of automatic settings for the parameters of swarm methods as the next stage of the future research study.

6.    Conclusions

The following research results were obtained.

A method for selecting swarm optimization algorithms and using swarm intelligence methods for solving a certain class of optimization tasks for industry-specific GIS, while considering the stationarity characteristic of industryspecific GIS, was developed. The method consists of 8 stages. During the application of the developed method, the following results were obtained:

• –    for solving tasks in stationary industry-specific GIS, the grey wolves method and the combined ant colony + flock of birds or grey wolves + bats methods are recommended;

• –    for solving tasks in quasi-stationary industry-specific GIS, differential evolution, particle swarm, and bee colony methods are recommended;

• –    for solving tasks in dynamic industry-specific GIS, the particle swarm method is recommended as well as the following combined methods: particle swarm + leaping frogs and a artificial immune system + bacterial search.

An information model of geodata has been developed. This model consists in formalized combination of the spatial and attributive components of geodata, which allows considering the relational, semantic and frame models of knowledge representation of the attributive component. In this way, the geodata of an industry become unified and this enables us to develop a technology of organizing geoscience databases.

A method of choosing optimization methods intended to work as part of the DSS of an industry-specific GIS was developed. It includes conceptual information modeling, the selection of optimization criteria, and the analysis and modelling of objective functions – all of these allow making the most reasonable choice of a swarm optimization method (or a set of methods).