Инкрементальные модели расчета пластинок, взаимодействующих с агрессивными средами

В работе рассматриваются инкрементальные математические модели упругопластического деформирования пластин средней толщины, работающие на изгиб в агрессивной среде, позволяющие.исследовать изменения напряженно-деформированного состояния (НДС) пластины на основе деформационной теории А. А. Ильюшина. Предлагается оценивать степень воздействия агрессивных сред на элементы конструкций с помощью деградационных функций секущего и касательного модулей, определяемых на основании экспериментальных данных.

Влияние агрессивной (рабочей) среды приводят к значительному изменению внутренней структуры и физико-механических свойств материала конструктивных элементов, работающих в этой среде [2; 6]. Экспериментальному исследованию зависимости скорости коррозии от напряженно-деформированного состояния (НДС) конструкции посвящено большое количество исследований. Многие авторы указывают на значительную сложность физико-механических процессов и невозможность создания универсальной математической модели.

При совместном действии эксплуатационной нагрузки и агрессивной среды появляется синергетический эффект, в результате которого НДС конструкции изменяется, а время от начала эксплуатации до наступления опасного состояния значительно уменьшается [1]. Проведенный анализ опубликованных работ, а также результатов обследования конструкций в различных условиях эксплуатации показывает, что при расчете необходимо учитывать воздействие агрессивных сред.

До настоящего времени общего метода расчета прочности и долговечности строительных конструкций с учетом воздействия внешней среды пока не существует. Известные нам методы основаны на различных экспериментальных данных, а выводы часто противоречат. В работе [5] показана методика создания частных моделей изгиба пластинок с нелинейно-упругими свойствами материала, учитывающая влияние величины концентрации агрессивной среды в материале. Опасным состоянием конструктивного элемента счита- ется момент достижения напряжениями в любой точке неповрежденной и поврежденной агрессивной средой частей сечения некоторого опасного уровня. Диапазон применимости модели — до момента наступления опасного состояния.

Для описания развивающейся неоднородности прочностных и деформационных свойств используется феноменологический подход. Феноменологические модели используют внешние признаки изменения (ухудшения) кого-либо свойства (прочности, жесткости) в результате деградации материала с течением времени или с ростом концентрации агрессивной среды в точке материала.

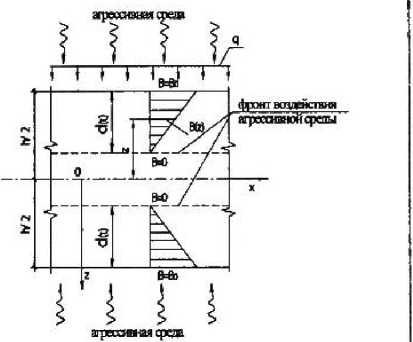
Рисунок /

Расчетная схема

На рис, 1 показана схема работы пластинки в агрессивной среде в момент времени / = (.. Среда действует на пластинку с двух сторон. Здесь В(; — концентрация ра- бочей среды на поверхности материала, 3 (!) — глубина проникновения агрессивной среды втолщу материала. В дальнейшем принимаем, что 3 (!) = «V t, где а — экспериментальный коэффициент, зависящий от пары ^материал—среда», q — интенсивность поперечной нагрузки, В (z) — концентрация агрессивной среды в произвольной точке материала, z— расстояние от срединной плоскости до текущей ординаты. Граница, где В (h/2~z) = 0, называется фронтом воздействия агрессивной среды.

Интегральной характеристикой свойств материала следует считать кривую деформирования, по характеру изменения которой можно судить о пределе прочности, деформационных свойствах материала, способности к разупрочнению и характере взаимодействия с агрессивной средой. Для построения модели необходимо иметь экспериментальные кривые деформирования при отсутствии агрессивной внешней среды, что позволит установить зависимость между интенсивностью напряжений о. и интенсивностью деформаций е. Результатом второй группы экспериментов является построение диаграмм деформирования для образцов, различное время взаимодействующих с агрессивной средой при несходных уровнях предварительного нагружения [51.

П. В. Селяевым [81 разработана методика экспериментальных исследований, позволяющая построить кривые деформирования для различных точек поперечного сечения образцов, которые взаимодействовали с агрессивной средой. Концентрация агрессивной среды, диффундирующей в материал образца в различных точках по направлению от поверхности образца к его центру, была различной, как и время взаимодействия образца со средой.

При проведении экспериментальных исследований варьировались состав полимербетона, концентрация и вид агрессивной среды. Результаты испытаний, проведенных по методике П. В. Селяева, представлены на рис. 2 в виде кривых деформирования материала а - е., а на рис. 3 — в виде изменений секущего и касательного модулей в зависимости от концентрации агрессивной среды в точке материала.

Из графиков видно, что наблюдаются резкое уменьшение секущего и касательного модулей при малых концентрациях всех рас-

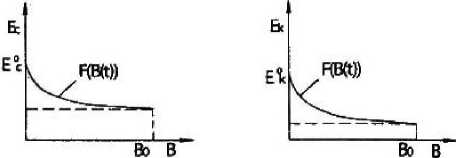
Рисунок 3 Результаты испытаний, проведенных по методике П. В. Селяева смотренных агрессивных сред и практически линейная зависимость при повышенных концентрациях этих сред.

За основу берем деформационную теорию пластичности для несжимаемого материала, в соответствии с которой имеем следующее физическое уравнение:

D^E^D,,             (1)

где D^— девиатор напряжений, D, — девиатор деформаций, Е*. — секущий модуль, Е*. — <7.1 е., а. — интенсивность напряжений, е. — интенсивность деформаций.

Для того чтобы получить инкрементальные физические уравнения, необходимо построить дифференциал Гато применительно к уравнению (1), который позволяет получить следующие физические соотношения в инкрементальной форме [5]:

.     ⁴=V.     ¹ a     ⁴f 1 '|сЕ*

' з V 2       2 г/м

Да = ^£*Где +^Де„"1 + ^[£ + -е,1^Д5;   (2)

&х=-Е>(в+-^-&В1 ” 3   ’ ЗоЯ где Д^, Му, Дт^— нормальные и касательные напряжения, Дед1 Дл^, Ду^— линейные и угловые деформации, E*t = da; / de. — касательный модуль, AS — приращение концентрации агрессивной среды.

Запишем дифференциальное уравнение равновесия пластинки Софи Жермен в инкрементальной форме:

^„^^..^ 0)

Зх¹ схау бу^{1                 1}

где ДА/, ДМ, ДМ^ — приращения изгибающих и крутящего моментов, Aq — приращение поперечной нагрузки.

Для приращений моментов справедливы формулы:

*/2                     Л/2

ДМ, = J An_izdz", АМ_у = J Aa_yzdz; -NII                    -NII

4/2

- Е0^ - те, ,

(И)

-Ml где h — толщина пластинки.

Считая справедливой гипотезу Кирхгофа, запишем деформации и приращения деформаций в срединной плоскости пластинки через прогиб и приращения прогиба по формулам:

где Е° — начальный модуль упругости материала, т — коэффициент, получаемый при обработке экспериментальных данных.

Выражение для секущего и касательного модулей примут вид:

Е9 -Е9- ть^ Е9 = Е9- Зт^.

a²w a¹^        „ a’ ft

£ — —z—r-; e =—z——; 7 = —zz---;

as_r = -z—--; As ,=-z— —, Ay_y=-2z

6W

йхду '

При использовании технической теории изгиба пластинок выражение для интенсивности деформаций имеет вид:

где №— суммарный прогиб, EW — приращение прогиба.

В соответствии с [8] в зоне деградации свойств материала концентрация среды изменяется от значения S_o на поверхности материала до нуля на границе фронта деградации. В зоне повреждения изменение прочностных свойств материала происходит от начального значения этого модуля на границе фронта деградации до наименьшего (на поверхности образца). Вид этой кривой определяется из решения уравнения массопереноса. Ввиду малой толщины поврежденного слоя и в запас прочности полагаем, что по толщине поврежденного слоя концентрация изменяется по закону треугольника. Из рис. 1 имеем:

Е(=^Е-2+еу + еА+^

Подставляя выражения (5) в (13), получим:     —-----------------------

2 f(d²FH

E, = ~^Z  —.

sW) 5²we²w бу¹ J ⁺ дх² ду²

Введем условное обозначение подкоренно-

го выражения в (14):

i² а²гг a²w

д2^

дхбу

2"

■ (15)

Тогда выражения для секущего и касательного модулей можно записать в виде:

Е^ ₌ £« _^L^ ^ ^ = £⁰-4мз¹[И^,(х,у)]. (16)

Перепишем (4) с учетом выражений (2) и (5):

B^z-O-Sh^1")

“.-^F

^-&B?dr, sb

Скорость роста концентрации рабочей среды в произвольной точке материала определяется по формуле:

4^» ^диД*^. ₂, AfSw isVy? be" ,, -  — + — £,zd2-—-+    —s-ABz^dr, 31 ^ 2 йг‘ J J ^А 31 ф^г 2 йк² ^

8В ^ Вфк-У) .

St 4а

Учитывая деградацию свойств материала во времени, выражения секущего и касательного модулей принимаем в виде:

Приращение концентрации агрессивной среды можно вычислить по формуле:

ЕВ = ™М.

e;=e:f№ е;=е;е(в^).

В результате обработки экспериментальных исследований П. В Селяев предложил записать функцию деградации в виде [8]:

ОД= exp(-XS(z)),

..... St

С учетом (10) отдельно рассмотрим интегралы, входящие в (17). После всех необходимых преобразований возможна следующая запись переменных интегральных характеристик:

где к — экспериментальный коэффициент, характеризующий степень деградации конструкционного материала.

На основании выражения (6) можно записать:

*/2

М2

А/2

IX^^l Е° р'^-з^-Дт^х.х)] je^ /dz ;

"4/1

-А /2

(19) 1

-“^

(^-i)-^>+^)- (ю)

7 ^ABz'dz = ^А J^^)

2, ЭВ 4а

Примем зависимость о -е, в точке материала в виде:

Введем дополнительные условные обозначения для коэффициентов:

a(f,z)= j e¹^ • z²dz; bQ,z)= je'^-^dz;

'^Ш                  —1/2           ZyQ)

*/2                    1,1            ^U/

c(t,z)= JV^-z⁴dz; dQ,z\= fe^-z’fifr.

-1/2                         -4/2

Переменные числовые коэффициенты (20) зависят от времени / и ординаты z, что позволяет описать условную жесткость в различные моменты времени по всей толщине мате риала.

Тогда интегральные характеристики переменных жесткостей обозначим:

/^ = Je,z’^ = е*^(Е⁶а(/)-4т[Ж(г_|у)]с(<));

7 ^АВг^^Г^-е^х ЗВ         4а

х^М^З-^ИЪз'ЗМ)-^^

С учетом (21) перепишем выражение (17):

_ 47^ 1 э2дИ . 47^ 1 аЧк'рл ., ко ._

Afs^w i^awY. 47а²ж i^if)

"''■Ч["ёГ'>2"ёР"У>*з1»г*2а?")

3 ЭхЭу 3 ЗхЭу 4а

^t^M.^f; 4а

После всех преобразований уравнение равновесия (3) пластинки в агрессивной среде можно записать в виде:

а»1 2 * J               ^T( a,1 2 ar* J ]           Vw где bq* — «фиктивная» нагрузка, отражающая влияние агрессивной среды.

v -^Н^Ш5Ш^)Ь (24)

Численная реализация уравнения (24) производится в два этапа. На первом производится пошаговое нагружение пластинки до заданного уровня нагрузки. При этом последовательно решаем уравнения вида:

a* (f ^Aw is'aw'i .1 a¹ (a’&w .1 a¹ [f^Aw la^w) .1 з а»’[( а’ 2 ay¹ J ^aaytaay^J*^^ бу’ *2 a? J^Z‘J“ 4^" (25)

^г’Г(^ ¹ ^" Vl ^ Г ^ау .], а" Г7a’Aw ₁i з’аЧЛ а7[( &’ *2 а^ J *]*&*,[ аду ^Л] ^ ^ ^ J J

Для решения задачи используем метод последовательных нагружений (МПН) [3], в соответствии с которым разбиваем процесс нагружения пластинки на ряд этапов (шагов). На каждом шаге задаем малое приращение нагрузки или приращения времени и решаем линейную задачу при известных накопленных за предыдущие шаги параметрах НДС пластины. Полное решение задачи по всем параметрам НДС пластин для заданного уровня нагрузки / концентрации среды получается как сумма решений на отдельных этапах нагружения.

Рассмотрим задачу изгиба пластинки, взаимодействующей с агрессивной средой, при использовании обобщенной кинематической модели С. П. Тимошенко (ОТ). Для этой модели считаем, что слои пластинки, параллельные срединной плоскости, не давят друг на друга, а прогиб пластинки не зависит от координаты z. Кроме того, нормальный элемент не меняет длины, но искривляется и поворачивается относительно срединной плоскости пластины.

При использовании модели ОТ напряженно-деформированное состояние пластинок за- висит от трех функций: прогиба пластинки W Lx, у) и двух углов поворота нормали на уровне срединной плоскости ^ (х, у\ уд (х, yY В этом случае удобно применять вывод соответствующих разрешающих уравнений задачи и граничных условий с помощью принципа Гамильтона — Остроградского.

Для применения этого принципа необходимо иметь выражения полной энергии деформирования пластинки и работы внешних сил. Чтобы получить выражение полной энергии изгиба пластинки, необходимы выражения для линейных и сдвиговых деформаций, которые в модели ОТ имеют вид:

5у, W Эу, ^У 3v 4zV6w э*ж\ йг ЗЛ ^ Дг йг ) ду 3* ( ду д/ )

На втором этапе по деформированной схеме производим расчет от достигнутого уровня нагружения при последовательном возрастании времени воздействия агрессивной среды на конструкционный материал. Вследствие этого прогиб пластинки растет, меняется ее НДС в соответствии с решением уравнения:

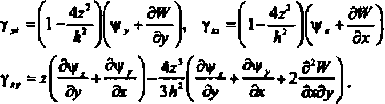
Все математические выражения запишем в полных значениях напряжений и деформаций. Это позволяет получить разрешающие урав- нения задачи и граничные условия в полных функциях, т. е. в наиболее информативном виде, а затем использовать метод последовательных нагружений (МПН) для инкрементального подхода к решению рассматриваемой задачи.

При использовании гипотез теории малых упруго-пластических деформаций А. А. Ильюшина физические соотношения для несжимаемого тела (при v = 0,5) с учетом деградации свойств материала F (t) принимают вид [9]:

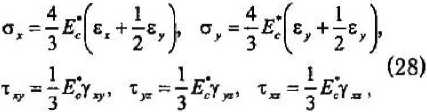
где ^, ег^ т ,тп, ге — нормальные и касательные напряжения.

В соответствии с принципом Гамильтона — Остроградского записываем для статической задачи уравнение:

С учетом пределов интегрирования 0 < х <  а,

О <  у < b, -h / 2 < х / 2 имеем:

6П= / j/k5e*+aA+T^r+T-^-+\^     (30)

• -А/2 G С

Варьируя в (30) функцию 'у, входящую в s^ у_п, у^, и применяя интегрирование по частям, находим:

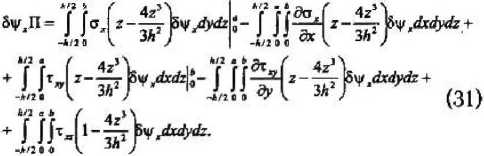
Варьируя в уравнении (30) функцию у/, входящую в Е_у, 7_ху, у_г, и применяя интегрирование по частям, получим:

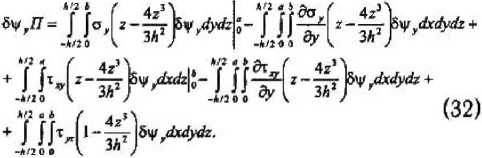
Вариацию работы внешних сил по прогибу W запишем в виде: я £

8_wv4 = JJ q(x,y^Wdxdy.         (34)

Подставляя уравнения (31), (32), (33) и (34) в уравнение (30) и в дальнейшем считая вариации 5W( ^, 5у произвольными, получаем систему разрешающих уравнений задачи изгиба физически нелинейной пластинки с учетом деградации свойств материала во времени [7):

*Р ^a-fof чА) , 4/2 ^OyHjf 4А)^ „ *£2 сА^(2) ( чА)^ J --1--у Л * f --V---7 Л + 2 J ■ —"У ^

4л аА ( з»2)   4/2 д-2 ( з/rj 4/2 atcy ^j

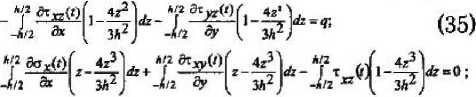
*/2 So/p f 4?). «Р ^хубХ чА) «У ,А чА), _ I ,— ^z--7 ® ⁺ j —£— 1--у «6- J т Ц 11--у & = 0.

4/2 ^ ( m²J 4/з & ( m^zJ 4/2 у¹ у за²)

Кроме того, применение принципа Гамильтона — Остроградского позволяет также получить естественные граничные условия задачи.

При использовании допущений ОТ формула для вычисления интенсивности деформаций приобретает вид:

^ = ^e' + E^E^ + l^+y^+y2) (36)

Введем условное обозначение подкоренного выражения (36):

Варьируя в (30) функцию IV, входящую в £, ^ У^/ y,z, У , после применения интегрирования по частям записываем:

И^ьх^е^ + Б^+е^ + ^ч-т^ +yt). (37)

В соответствии с деформационной теорией пластичности считаем, что зависимость о-е, аналогична экспериментально полученной диаграмме деформирования, т. е. зависимости а — е. При аппроксимации экспериментальной диаграммы деформирования материала куби- ческой параболой выражение секущего модуля для модели ОТ можно записать в виде:

Е^^-^^х1У,г

Рассмотрим отдельно каждый интеграл, входящий в (35):

-й/2

-кП

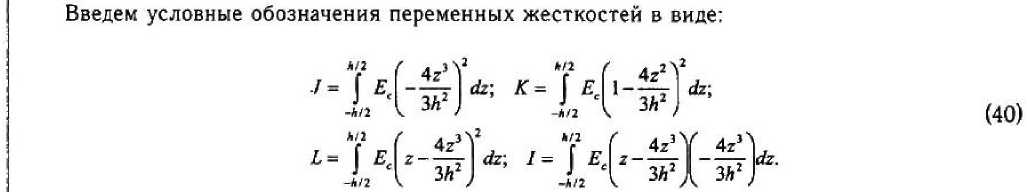
После необходимых преобразований выражений (39) систему уравнений равновесия (35) пластинки, работающей в агрессивной среде, для модели ОТ на этапе нагружения пластинки малыми ступенями распределенной поперечной нагрузки МПН можно записать в виде:

Рисунки к статье В. В. Петрова, О. В, Пениной и П. В. Селяева «Инкрементальные модели расчета пластинок, взаимодействующих с агрессивными средами»

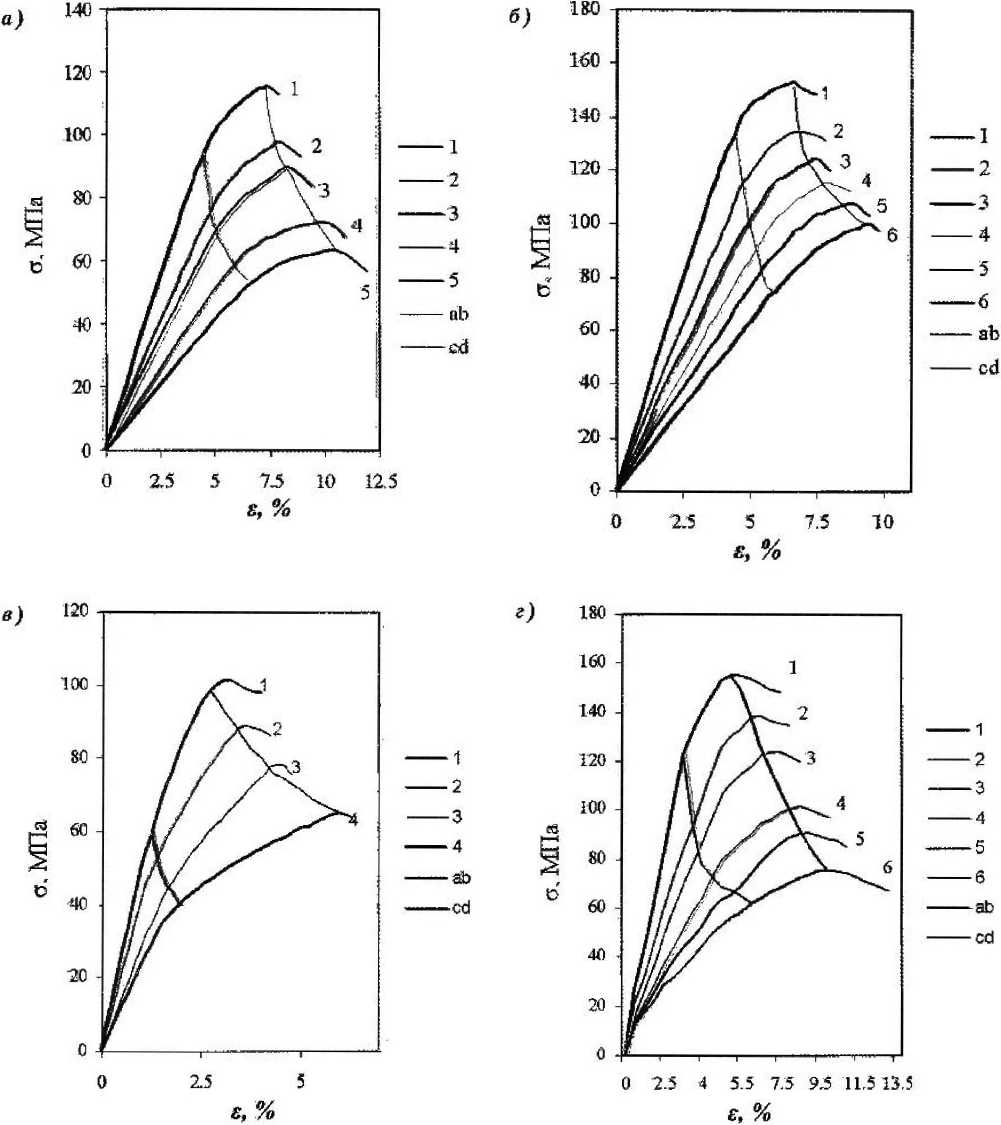
Рисунок 2

Диаграммы деформирования бетонов: а, б — полиэфирных, выдержанных в воде; в — полиэфирных, выдержанных в водных растворах серной кислоты; г — эпоксидных, выдержанных в водных растворах едкого натра; 1 — в начальный момент времени, 2 — 10 суток выдержки в агрессивной среде, 3 — 50 суток выдержки, 4 — 170 суток, 5 — 265 суток, 6 — 395 суток

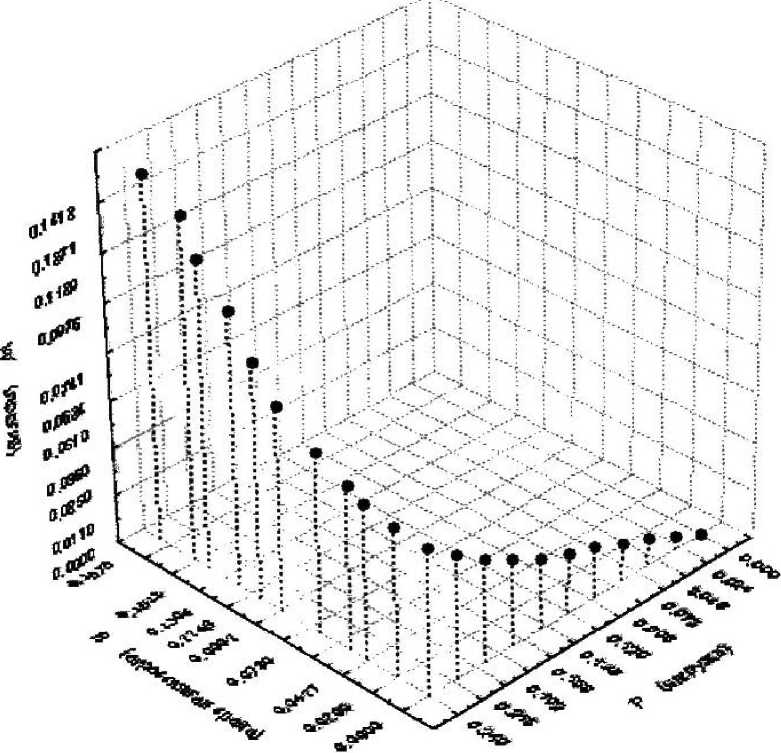
Рисунок 4

Методика вычисления расчетов

пластинки на изгиб.

работающей при воздействии агресивной среды для модели Кирхгофа — Лява

(MX^”)-'

0 =

УХ^ЧХ*^\Ч-»Х”)-¹-"Х"'')УЧ.'Х'^,'^*Х'^м'^!У^,+ ХХ^Л'^^м^^^'У^’^А'^х^* ^ ■ ^♦\-^ -7 ♦(ч^ ^ «^ - (>^Y * >v))/ ₊

♦(Г^Л'^^Т^гТ^Н1^^)^

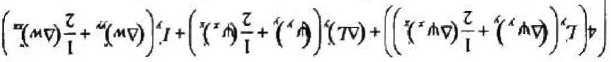
'             (мч^^-смч'^^-'

< ад^)+1^)^ ^Т^⁺ т^⁺ ^^^^^^^^^^-ь^^^^^^^^)

X Х‘^ * Г-^у? *(“wf +1 л))м * (>V)^ л«у)) ^ ^t^rT^^T^rl'^H¹^¹^ /(l^rK-v^^t^T^'^^^t'^r^^'^,

■Ь^£-

(1/й) +V^JVM* ^^^^^ t^)J f             cn*TWt

ЛТ^т^у* ч»)Х^ * "i-v». ^ r?)₊>v)vj

z+

^‘^^T^y^^ri^-^r^^XriVW.^*

(IH

('I^T^^^^vi^^y^l^^l'^/vt'

»(T*v)y*T^)xT^T«)9WXTXv)+^^^

ХИ^Ч'^^ХК'^-Х'^'/^Му+ад]!/»)*

^i“’)ri'“’))^^x'^f^t('^,))‘i'^v)^t(r'‘^5,)rt'*^"^/4-^4»)f* l^^-v)^ 1^У+( I'^T- T^/vt ^I'^Y* T^I\4* -X^X^)^-^ "X^yr¹ ,l>^tT^X^XT*^⁺T*v^^,/*(l4>f^-4)l^» ♦(I^wjv+^T^^

Для аналитического исследования и сокращения в дальнейшем объема записи перепишем уравнения (41) в символическом виде, где смысл введенных обозначений ясен из анализа этих уравнений:

• 4.4 + 2В - С = ЗДл; D = 0; Е = О (42)

На втором этапе по деформированной схеме производим расчет для достигнутого уровня нагружения при последовательном возрас тании времени воздействия агрессивной среды на конструкционный материал. После достижения нагрузкой заданного уровня q и решения системы уравнений (41) становятся известны значения функций И/, у,, уу, что позволяет да-лер исследовать задачу изгиба пластинки от воздействия агрессивной среды во времени, которое меняется с шагом AZ в соответствии с решением системы уравнений (43).

4Л*2В-С = ЫХ(4Л + 2В-С)+

(?Ц8д4*Л)+^14<^)+«^^^

♦И^ДтП,^^^*-^^1^)*

* а(у д 4^д)х «„pn Ч^Н^д^дЛ - «^l ^д> /(frx 4<гл)*^ *|^x„J

+ 4/^”**

УХ^Д^ЛУМКУЖЬ,*'

♦И^ХД^ЖДХ,!)

^i^tui^^xxx)

Ж-Ч^Ук^л^хУ Ж,+^Х>к*Д^хУ

D = MDX + Afke^x

<4(м4^<(фх4ба)^

т^^^+^Д^ДХгНИ,*

+L^A,*t,\y21frVK^.W\)

E = МЕХ + МХе”'ь x

x

x 2 'V 2     ) V » 2

*4<^4(^]+£W,bW,>2«(n + 4,1*ЦИ1П*

^^l+exX^v^+wll

Поставленная задача изгиба физически-нелинейной пластинки с учетом величины концентрации агрессивной среды в материале при соответствующих граничных условиях, при применении метода конечных разностей

(МКР) описывается замкнутой системой линейных алгебраических уравнений, записанных в инкрементальной форме.

На каждом шаге расчета производится проверка наступления опасного состояния в

Таблица

Результаты расчета, пластинки на изгиб, работающей при воздействии агрессивной среды для модели Кирхгофа — Лява наиболее нагруженной точке материала конструкции. В случае возникновения опасной величины напряженного состояния расчет прекращается. Результаты расчетов по предложенной выше методике с использованием модели Кирхгофа представлены в табл. На рис. 4 приведен трехмерный график, иллюс

трирующий предложенную методику решения поставленной задачи.

В заключение отметим, что на основе шагового МПВП В. В. Петрова и МКР разработан универсальный эффективный алгоритм расчета нелинейно-упругих пластин, работающих в агрессивных средах.

Шаг	Величина нагрузки, Р	Концентрация агрессивной среды.	Прогиб, В?
1	0,0240	0,0000	0,0000
3	0,0720	0,0000	0,0160
6	0,1440	0,0000	0,0300
8	0,1920	0,0000	0,0430
10	0.2400	0,0000	0,0610
11	0,2400	0,0209	0,0624
13	0,2400	0,0522	0,0682
16	0,2400	0.1148	0,0976
18	0,2400	0.1513	0,1271
20	0,2400	0,1878	0,1506