Инкрементальный подход к физически нелинейному расчету железобетонных балок-стенок с трещинами

Существенной проблемой численной реализации физически нелинейных моделей и методов расчета железобетонных конструкций является сходимость итерационных процессов. Как показывает опыт конечно-элементного анализа [3], после образования трещин требуется от 50 до 100 итераций на каждом шаге нагружения для обеспечения 5 % точности решения задачи в перемещениях.

В настоящей работе рассматривается построение инкрементальной модели железобетона с трещинами на основе общей механики железобетона [1], которая прошла большую экспериментальную проверку и принята в качестве основы для сопоставления результатов при переходе к инкрементальным физическим соотношениям.

В нелинейной анизотропной модели балки-стенки учитываются нелинейный характер деформирования бетона и арматуры и образование трещин, что приводит к приобретаемой анизотропии. Согласно этой модели, связь между деформациями и напряжениями представляется в виде:

' Ex C11  C12   C13 Ox Ey ■ = C12  C22  C23 X • σy ■,                      (1) Yxy . _ C13   C23   C33 _ T Txyy где [C] – симметричная матрица податливости железобетона.

При формировании матрицы [C] учитываются анизотропия, физическая нелинейность бетона и арматуры, связи зацепления берегов трещин, влияние сцепления арматуры с бетоном между трещинами на ее диаграмму растяжения (на основании методики В. И. Мурашева) и другие факторы нелинейности. Физические соотношения (1) и коэффициенты матрицы податливости [C] устанавливаются на основании анализа напряженно-деформированного состояния малых элементов балки-стенки. При этом выделяются четыре стадии работы материала:

• •    линейная без трещин (упругая стадия работы бетона и арматуры);

• •    нелинейная без трещин (с учетом влияния пластических деформаций в бетоне);

• •    с трещинами при упругой работе арматуры в трещинах;

• •    с трещинами при работе арматуры за пределом упругости.

Трещины в бетоне образуются по площадкам действия главных растягивающих напряжений, когда их значение достигает предела прочности бетона на растяжение в условиях плоского напряженного состояния (нарушения критерия

прочности). Физические соотношения между вектором деформаций и вектором напряжений имеют нелинейный характер и существенно зависят от величины достигнутых усилий в бетоне и арматуре. Применение шагово-итерационной процедуры решения задачи позволяет получить полную кривую равновесного состояния конструкции и проследить всю историю ее работы под увеличивающейся нагрузкой вплоть до разрушения, но требует очень большого объема вычислений. Этот недостаток становится особенно ощутимым при решении большеразмерных задач. Шаговые методы при малом увеличении параметра нагрузки позволяют получить приближенную кривую равновесных состояний, однако такой подход при использовании секущих характеристик жесткости приводит к существенным погрешностям.

Рассмотрим решение физически нелинейной задачи расчета железобетонных балок-стенок малоитерационным методом в конечных приращениях. В этом случае система физических соотношений в секущих модулях приводится к системе физических соотношений в условно касательных модулях по методу [2]. Исходная система физических соотношений с использованием секущих характеристик жесткости на j -м шаге имеет следующий вид:

р E xJ		■ C 11J    C 12J    С 13’"		'
E yJ	^ =	C 12 J    C 22 J    C 23 J	X •	O y	■ .                 (2)
, Y xyJ		_ C 13 J    С 23 J    С 33J .		V^ xy

Аналогичная система на j+1 -м шаге:

E xJ + 1		■ C 11 J + 1     C 12 J + 1     C 13 J + 1 "		° xj + 1
E yJ’ + 1	■ =	C 12J’ + 1     C 22 J’ + 1     C 23 J’ + 1	X •	° y • ■	■ . (3)
E xyJ’ + 1		_ C 13J’ + 1     C 23 J’ + 1     C 33 J + 1 _		v T xyj + 1

Вычтем из системы (3) систему (2): ^{( E} x +1 ^{— E} x ) = ⁽C 1 1 j + 1 O j + 1 ^— C 1 j ° g' ^{) +}

+ ( C 2 J - \°;H ^— C 12j ° yj) ^{+ ( C}13J + 1 ° у +1 ^— C 13 A y );

⁽ £ yj + 1 — J = ⁽ C 2 j +1 < 7 X7 + 1 ^— c 12j ° xj ) ⁺

⁺ ( C ’2 j + 1 ^O y + 1   (A'O yj ) ^{+ (}C 23j ' +1 ° у +1   C 23j^xy )

( Y xyj + 1 - Y xy ) = ( C 13 j + T xj + 1 — C 13j T xj ) +

4 ^C 23 j'Ay + 1 C B j A) ^{+ (C} 33j'Axy + 1 C 33j A y )- Обозначим

Ae „ ' + 1 = E x,' + 1 — E xj ;

■V'. '

= p .1 — p

^E yj + 1 ^E yJ ;

^AE xyj 41     ^E xyj 41    ^E xyJ ,

A o.. + 1 = о _ч + 1 — o „ J ; A o y + 1 = O y + 1 — O y ■; At , =

^T xy +1 ^T xyj .

Разделим и одновременно умножим первые разности в правой части (4) на Ao _{xj + 1}, вторые -на Ao _{yj + 1}, третьи - на AT _{xyj + 1} и обозначим:

pк   _ C11J'+1Oxj+1 C11j'°j kJ    _ С22j+1Oyj+1   С22jOyj ch,+ =       42         ’ C22 J+1 =       42

^AO xj’ +1                            ^AO yJ + 1

... к _ ¹ I C 12 j'+l ° yj +1    C 12j^Oyj     C 12j'+l°xj’ +1    C 12 j’^Oxj |.

C12 j+1 = ~ I                                 1; I

21      A^y+1                A^xJ+1

к _ ¹ | ^C 13y + 1 T xyj +1    C 13y ^T xyJ

^{C 13 J + 1} = 2

C 13 J +1 ^O xj +1 ^— C 13 J ^O xj I _ A O ’     J’

AT xyJ + 1

С к , =1 1 ~ C ^J 2 I

23 J + 1 ^T xyJ +1    C 23 J’ ^T xyJ     C 23 J +1 ° )j +1    C 23 J ^O yj

k

С 33 +1 ⁼

C 33 j + \ Т xyJ +1

AT xy + 1

^— С 33 J T xyJ

A a y +t

;

AT xyJ +1

.

С учетом выражений преобразуется к виду:

(5) и (6) система (4)

^AE xj + 1

• ^{A E} .

_^A Y xyj + 1

C k 11 J + 1	C k 12 j +1	C k 13 j + 1 "		" AO xj + 1 '
C k 12 j +1	C k 22 j +1	Ck 23 j +1	X •	AO yj + 1
C k 13 j +1	C k 23 j +1	C k 33 j + 1 _		AT xyj + 1

. (7)

•

При решении задачи шаговым методом с равными шагами по нагрузке в зависимостях (6) можно приближенно принимать:

^AO xj’ + 1 ” ^AO xj = ^O xj ^{— O} xj — 1 ; аналогично

Ao + + A o ; AT xyJ + 1 = AT xyj ;

^O xj’ + 1 ” ^O xj ^{+ AO} xj ^{; O} yj’ + 1 ” ⁽⁸⁾ = ^O y ■ ^{A o} ; T xyJ + 1 « T xyJ ^+A T xyJ .

В дальнейшем, решая задачу по системе (7), получаем несколько иные значения A a_xi +1 , A a vi +1 , A T_xvi+ 1 , которые используем при вычислении жесткостей по формулам (6) на J+2 -м шаге.

Смысл указанных выше формальных преобразований заключается в том, что при использовании выражений (8) погрешности на шагах нагружения накапливаются небольшие и на каждом шаге можно обойтись одной итерацией.

Предлагаемый малоитерационный подход к физически нелинейному расчету железобетонных балок-стенок в конечных приращениях реализован в виде алгоритма и компьютерной программы расчета. Адекватность предлагаемого подхода оценивается путем сопоставления расчетных и экспериментальных данных, характеризующих работу конструкции в процессе нагружения. Были исследованы шагово-итерационные процедуры, построенные на базе секущих матриц жесткости, и шаговые процедуры с использованием касательных матриц (матриц с касательными элементами жесткости). Для сопоставления предлагаемых методик был осуществлен численный эксперимент, в ходе которого рассчитывались железобетонные балки-стенки из опытов М. П. Нильсена [4]. Балки-стенки высотой h = 100 см, толщиной t = 8 см и пролетами l = 100 см (балка-стенка № 101) и l = 200 см (балка-стенка № 103) были испытаны на кратковременную нагрузку. Армирование балок-стенок осуществлялось однородной сеткой из стальной проволоки диаметром 6 мм и шагом 100 мм (μx = μv = 0,0035). Физико-механические свойства арматуры, схемы армирования балок-стенок и физико-механические свойства бетона приведены в работе [3].

Для расчета симметричные части балок-стенок № 101 и 103 были разбиты на 51 и 101 прямоугольных КЭ, соединенных 68 и 123 узлами соответственно. На рис. 1 и 2 представлены графики прогибов балок-стенок. Как в опыте, так и в расчете балки-стенки загружались до разрушения. В балке-стенке № 101 опытная нагрузка трещинообразования составила 145 кН, расчетная – 120 кН. В балке-стенке № 103 опытная нагрузка трещинообразования – 78 кН, расчетная – 90 кН. В эксперименте и в расчете образование первых трещин не привело к существенному нарастанию прогибов. Как следует из графиков (рис. 1 и 2) и анализа напряженно-деформированного состояния, нелинейность де- формирования резко возрастает с началом текучести растянутой арматуры, сокращением высоты сжатой зоны и сопровождается нарастающим раскрытием трещин. Как в опыте, так и в расчете разрушение балок-стенок явилось следствием текучести продольной растянутой арматуры и исчерпания прочности бетона сжатой зоны.

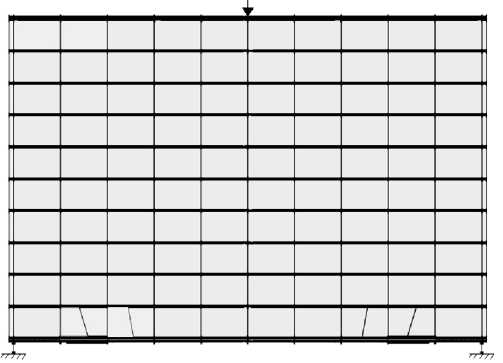
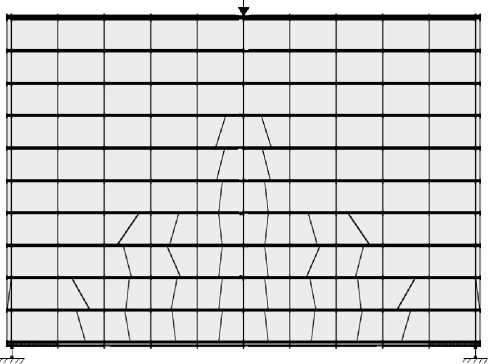
Расчетные схемы балок-стенок, совмещенные со схемами образования и развития трещин, представлены на рис. 3 и 4.

Теоретическая кривая прогиба, рассчитанная по предлагаемой методике, по характеру деформирования полностью соответствует опытной с расхождением в отдельных точках до 15 %. Отклонение теоретической кривой, полученной шагово-итерационным методом с использованием секущих характеристик жесткости, составило 7 %. Разрушение балок-стенок сопровождалось текучестью арматуры растянутой зоны, что также соответствует опытным данным.

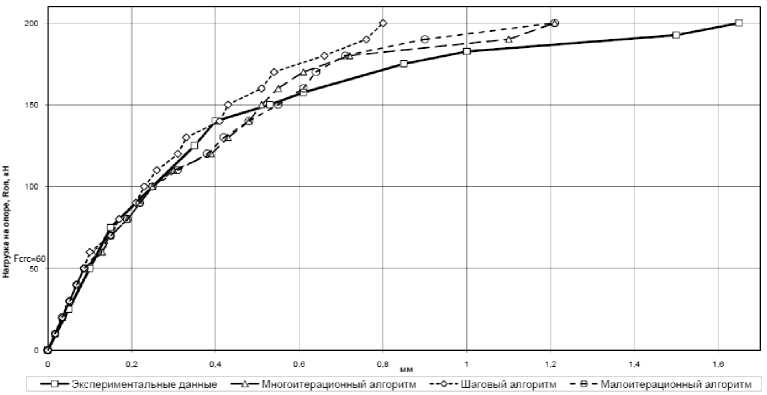
Рис. 1. График прогибов балки-стенки № 101

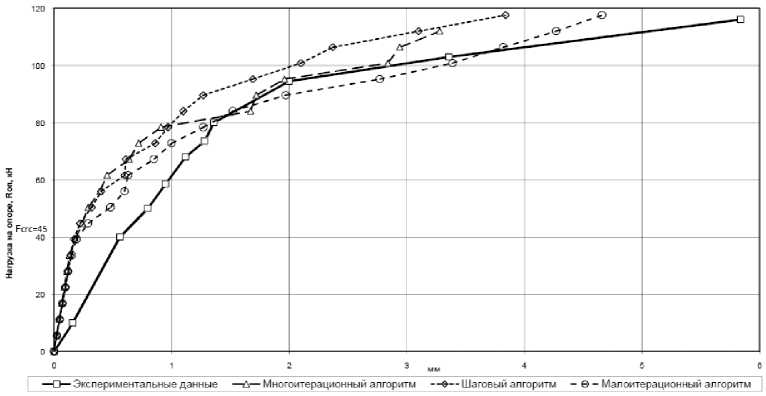
Рис. 2. График прогибов балки-стенки № 103

F = 120kH

дение с результатами физически нелинейного расчета по шагово-итерационному методу не превышает 8 %. Хорошее согласование опытных и теоретических прогибов, вычисленных с использованием предлагаемых физических соотношений в инкрементальной форме, а также последовательности образования и развития трещин во всем диапазоне увеличения нагрузки практически до разрушения позволяет рекомендовать малоитерационный метод для численного моделирования сложных пространственных железобетонных конструкций, работающих в условиях плоского напряженного состояния.

F = 340kH

F = 400kH

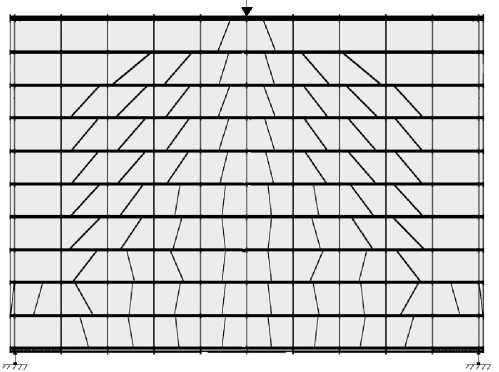
Рис. 3. Схемы образования и развития трещин в балке-стенке № 101

Выполненная проверка эффективности предложенного метода построения физических соотношений в конечных приращениях и перехода от секущих характеристик жесткости к касательным на примере расчета экспериментальных балок-стенок показала высокую эффективность малоитерационного шагового способа решения физически нелинейных задач железобетона. Расхож-

F = 90kH

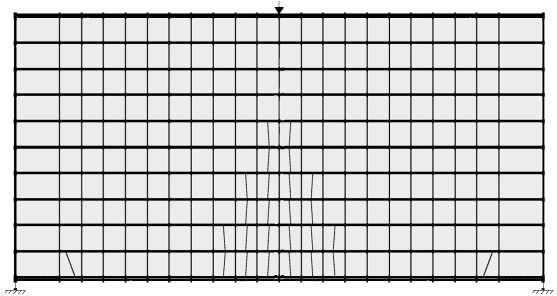
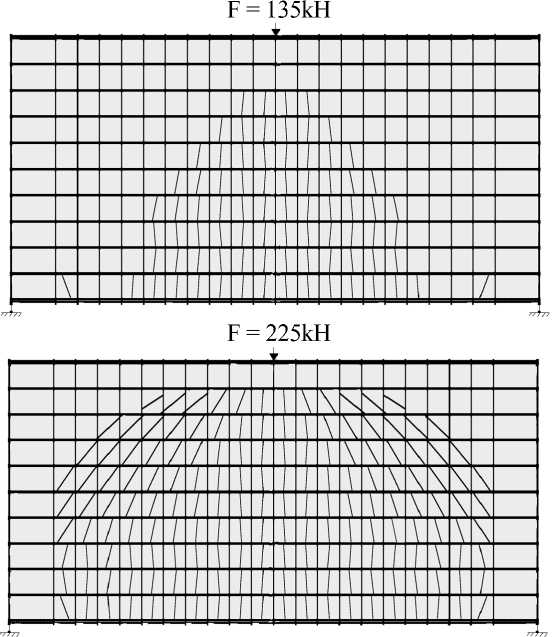
Рис. 4. Схемы образования и развития трещин в балке-стенке № 103

Работа выполнена при финансовой поддержке РФФИ.