Инновационная технология расчета обобщающих характеристик плоских криволинейных в плане тел

В практике производственных малых предприятий возникает довольно часто потребность в определении обобщающих характеристик (площади, объема и веса) криволинейных в плане плоских тел постоянной толщины, вычисление которых легко автоматизировать с использованием компьютерных технологий.

В современных условиях широкого распространения офисных компьютеров, оснащенных, как правило, пакетом прикладных программ MicrosoftOfficeWord 2007 и 2010, вычислительный процессор которого легко решает задачи подобного типа.

Представление о вычислительных возможностях программ Microsoft Word дает следующий пример вычисления площади А, объема V и веса G криволинейного в плане тела, ограниченного кривыми не выше второго порядка при произвольном числе их.

Важно, при этом, подобную программу может легко создать любой пользователь компьютера, хорошо освоивший алгоритм традиционного метода решения задач подобного типа, знакомый с понятием криволинейной трапеции, из которых и состоит криволинейное тело.

Площадь любой криволинейной трапеции определяется по одной и той же формуле (в чем и состоит мощь высшей математики) определенного интеграла вида:

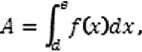
где ; 0x3 — функция, ограничивающая тело сверху (в данном случае это полином не выше второго степени вида у = ах¹ + bx + с ); d и е — пределы его интегрирования.

Интеграл от указанной функции и любой другой функции, которая является частью ее, в общем виде для криволинейной трапеции (элемента плоского криволинейного тела) равен:

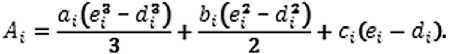
Площадь всего криволинейного тела равна сумме площадей всех криволинейных трапеций, образующих тело:

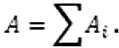
Объем i-той части криволинейного тела постоянной толщины рассчитывают по обычной формуле вида:

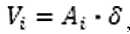
где О — толщина тела.

Объем всего криволинейного тела равен сумме объемов всех составляющих его частей:

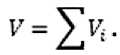
Вес i-той части криволинейной тела рассчитывают также по обычной формуле:

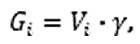
где У — объемный вес материала плоского тела.

Вес всего криволинейного тела равен сумме весов всех составляющих его частей:

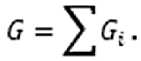
В качестве примера рассмотрим методику и программу вычисления указанных обобщенных характеристик для плоского криволинейного в плане тела, границы которого задаются следующей системой квадратных парабол и прямых линий:

Верхняя граница каждого элемента задают уравнением в своей системе отсчета, поэтому все интервалы исчисления всех элементов начинаются с нуля и равны ширине соответствующего элемента фигуры:

y ₁ = x ² – 5 x + 8 на интервале 0 ≤ x ≤ 2;

y ₂ = 2 x + 2 на интервале 0 ≤ x ≤ 3;

y ₃ = x ² – 4 x + 8 на интервале 0 ≤ x ≤ 4;

y ₄ = x ² на интервале 0 ≤ x ≤ 2;

Толщину листового тела принимаем равной δ = 0,01 м, а объемный вес

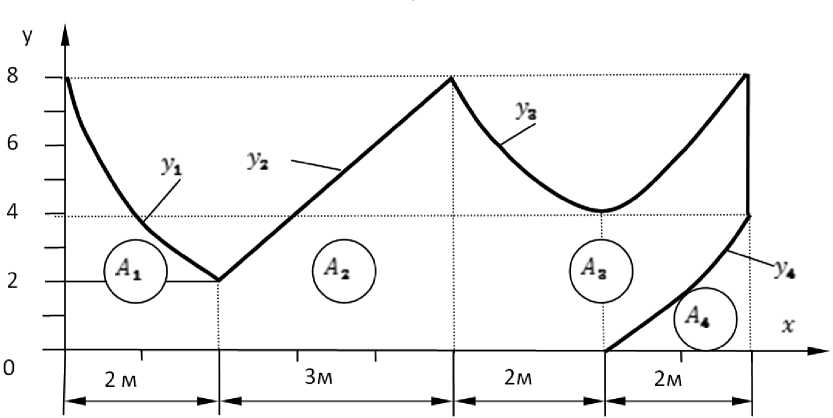
По этим формулам, используя инструмент «Рисунок», создаем план криволинейного тела, показанный на рис. 1.

Вычислительная таблица является вычислительной программой, в которой вычислительные команды расположены во втором слое под числами в белых клетках и реализуют, указанные выше формулы.

Согласно заданным уравнениям границы тела, оно состоит из четырех частей А₁ , А₂ , А₃ , А₄ и для каждого из этих элементов (криволинейных трапеций) выделяем отдельную строку в вычислительной таблице для ввода исходных данных и вычисления обобщающих характеристик его.

Исходные данные записывают в клетках, выделенных серым цветом каждого элемента.

Кроме того в строке «Исходные данные» предусмотрен ввод дополнительных исходных данных, общих для всего тела: толщины его δ и объемного веса материала, из которого создано это тело γ.

Рис. 1. План криволинейного тела из четырех элементов

Таблица 1. Обобщающие характеристики криволинейного тела

δ	0,01	Исходные данные				Характеристики элементов
γ	1300
i	a	b	c	d	e	Ai	Vi	Gi
1	1	-5	8	0	2	8,67	0,087	113,10
2		2	2	0	3	15,00	0,150	195,00
3	1	-4	8	0	4	21,33	0,213	276,90
4	1			2	0	-2,67	-0,027	-35,10
5						0,00	0,000	0,00
Площадь всего тела, A , м2						42,33
Объем всего тела, V , м3						0,423
Вес всего тела, G , кг						549,90

Следует обратить внимание, что в строке для четвертого элемента все обобщенные характеристики имеют отрицательные значения, так как этому элементу соответствует пустота, кроме того пределы интегрирования в этом случае вводятся в обратной последовательности (сначала d=2, а затем e=0).

Вычислительная программа рассчитана на вычисление обобщенных характеристик криволинейного тела, состоящего из одного – пяти элементовиз одного и того же материала при одной и той же толщине. Исходные данные для каждого элемента являются коэффициенты аналитических выражений, описывающих криволинейный контур тела и границы интегрирования, которые записывают в их естественной последовательности. Если в уравнении кривой отсутствует тот или иной коэффициент, то в таблицу вводят ноль или просто оставляют соответствующую клетку пустой. Исходные данные вводятся по строчкам, при этом последовательность расположения элементов криволинейного тела по строчкам вычислительной таблицы произвольная.

После ввода исходных данных, щелкают курсором мыши по маркеру таблицы, и она вся выделяется серым цветом. После этого нажатием клавиши «F9» запускают программу на выполнение. После окончания расчета вычислительная таблица имеет вид, показанный в табл.1.

Чтобы произвести расчет для нового набора данных, следует выделить исходные данные предыдущего расчета, расположенные в ячейках вычислительной таблицы, выделенных серым цветом, и нажать клавишу «Delete». Затем вводят в эти ячейки исходные данные нового расчета.Далее операции повторяются, т.е. щелкают по маркеру вычислительной таблицы и нажатием клавиши «F9», запускают программу на выполнение вычислений с новыми данными.

При выделении данных предыдущего расчета надо быть внимательным, чтобы наряду с ячейками для исходных данных не были выделены вычислительные ячейки (три последних столбца вычислительной таблицы). В этом случае вместе с исходными данными будут удалены вычислительные команды, которые находятся во втором слое и в обычном режиме не видны.

По рассмотренной методике можно составить программу для определения обобщенных характеристик для тел, ограниченных другими функциями, как полиномиальными более высокого порядка, так и принципиально другими кривыми, например гиперболическими или сочетанием нескольких видов функций. Можно также составить программу для расчета обобщенных характеристик тел ступенчатой толщины или для тел не только переменной толщины, но и изготовленных из различных материалов, определения большего числа обобщенных характеристик, таких как координат центра тяжести тела, величин статических моментом и моментов инерции сложных поперечных сечений и т. д.

Разработанная программа может найти применение не только в учебном процессе, но и на малых торговых предприятиях, при раскройке материала, в том числе на швейном производстве малого бизнеса, при создании сложных листовых конструкций, в том числе листовых емкостей различного назначения и т. д.