Инновационный рейтинг регионов в радиоэлектронной промышленности: построение и верификация с использованием машинного обучения

EDN:                                ISSN 2413-1407 (Print)

Ориентированность отечественной экономики на технологическое лидерство требует применения новых, современных, подходов к анализу деятельности приоритетных отраслей, к числу которых относится радиоэлектронная промышленность (РЭП). Чтобы разработать актуальные методы управления ее развитием в регионах страны, необходимо исследовать большой объем данных ( Big Data ). Применение методов машинного обучения позволит построить инновационный рейтинг регионов, что будет способствовать принятию оптимальных управленческих решений государством и крупными частными компаниями в отношении планирования инновационного развития отрасли.

Необходимость сочетания государственных и цифровых инструментов и методов регулирования социально-экономических отношений в условиях трансформации экономической системы обоснована Л. П. Зеньковой и О. В. Машевской1. Однако применение инновационных рейтингов регионов сопряжено с определенными трудностями [1–4]. Предпринят ряд попыток учесть при построении таких рейтингов особенности выбранных территорий2 [5–8].

При построении и применении рейтингов для отрасли РЭП важно учитывать ее особенности. Результаты исследований, например3 [9], показывают, что размер рынка, развитие науки, техники и организации, качество человеческих ресурсов, а также факторы политики и информационной среды влияют на развитие отечественной электронной промышленности.

Построение инновационного рейтинга регионов в отрасли РЭП является типичной задачей многоуровневой классификации в машинном обучении. В этой области создано достаточно много эффективных методов.

Машинное обучение выступает ключевым компонентом в более широкой области искусственного интеллекта, которая использует статистические методы для наделения компьютеров способностью учиться и принимать решения автономно, без необходимости явного программирования. Оно основано на концепции, что компьютеры могут получать знания из данных, выявлять закономерности и делать выводы с минимальным вмешательством человека [10]. В этой области существуют различные типы алгоритмов машинного обучения: контролируемое, неконтролируемое, полуконтролируемое и обучение с подкреплением [11].

Метод классификации применяется для классификации истинного либо ложного результата или нескольких классов любого прогноза. Логистическая регрессия, наивный байесовский алгоритм ( Naive Bayes ), k ближайших соседей ( k-Nearest Neighbors, KNN) , деревья решений ( Bagged Trees ), машины опорных векторов ( Support Vector Machine, SVM) и искусственная нейронная сеть ( Artificial Neural Network, ANN) - вот некоторые из популярных алгоритмов классификации в различных областях⁴.

Цель исследования состоит в построении и верификации инновационного рейтинга регионов страны в отрасли РЭП с использованием машинного обучения. Преимущество авторского подхода заключается, во-первых, в построении рейтинга регионов конкретно для отрасли радиоэлектронной промышленности, а, во-вторых, в применении для этого более точного подхода, использующего последние достижения в области машинного обучения. В исследовании хорошо показали себя такие методы классификации в машинном обучении, как точный гауссовский SVM ( Fine Gaussian SVM), подпространство KNN ( Subspace KNN) и решающие деревья.

ОБЗОР ЛИТЕРАТУРЫ

В области машинного обучения в последнее время появилось много эффективных решений, в частности новый метод классификации для многоуровневых многометковых наборов данных, основная цель которого – повысить точность задач классификации, включающих несколько классов и меток [12]. Эксперименты продемонстрировали его эффективность в ряде известных наборов данных со средней точностью 85,9 %.

• Х. Таном [13] сравниваются пять традиционных классификаторов машинного обучения (Gaussian Mixture Models, Random Forest, SVM, XGBoost и Naive Bayes) и показано, что классификатор на основе SVM имеет самую низкую точность при обработке текстовых данных для применения задачи классификации текста.

Результаты работы Дж. Г. Переза и М. Баллеры5 свидетельствуют о том, что алгоритм Gradient Boosted Trees как один из методов машинного обучения превзошел другие алгоритмы, достигнув высокой точности классификации, а именно 91,58 %; на 2-м месте – подход Deep Learning (глубокое обучение), продемонстрировавший точность 90,48 %.

Сравнительное исследование, построенное с учетом четырех различных показателей производительности, показывает, что, за исключением алгоритма дерева решений, предлагаемые методы машинного обучения с подробными алгоритмами предварительной обработки хорошо работают для классификации публикаций по категориям на базе заданного текста6.

В публикации С.-Л. Лина для применения машинного обучения предлагается метод средней гауссовой машины опорных векторов (SVM), который создает пространство признаков путем извлечения характеристик сигнала вибрации, собранного на месте с опорой на опыт [14].

В статье К. Ма и др.⁷ рассматривается алгоритм KNN на основе подпространства признаков (Feature Subspace KNN). Во-первых, названный алгоритм решает все подпространства признаков согласно распределению обучающих выборок в пространстве признаков, чтобы гарантировать более высокое сходство выборок в одном подпространстве. Во-вторых, соответствующее подпространство признаков сопоставляется с выборками тестового набора. Таким образом, сначала выполняется поиск k ближайших соседей в заданном подпространстве, что повышает точность и эффективность алгоритма.

Случайные леса, основанные на деревьях решений, в сочетании с идеями агрегации и бутстрепа представляют собой мощный непараметрический статистический метод, позволяющий рассматривать в единой и универсальной структуре проблемы регрессии, а также двух- и многоуровневой классификации [15].

Построение эффективных деревьев обычно является сложным и трудоемким процессом, особенно для наборов данных с высокой дисперсией. Ряд авторов сосредоточили внимание на вопросах улучшения их производительности, надежности и стабильности8 [16].

В работе И. Ибаргурена и др. [17] метод PCTBagging представлен как гибридный между бэггингом и консолидированным деревом, так что в нем частично сохраняется свойство понятности последнего, а также улучшается дискриминационная способность. Консолидированное дерево сначала разрабатывается до определенной точки, а затем для каждого образца выполняется типичный бэггинг.

В отличие от других, для методов дерева решений эффективность прогнозирования ансамблевых методов выше, чем неансамблевых. Иначе говоря, деревья решений, использующие ансамблевые методы, обеспечивают лучшую эффективность их применения, в сравнении с KNN и линейным регрессионным анализом [18].

Х. Джафарзадэ и соавторы изучают возможности различных алгоритмов ансамблевого обучения, известных как алгоритмы бэггинга и бустинга (включая Adaptive Boosting (AdaBoost), Gradient Boosting Machine, XGBoost, LightGBM и Random Forest), для классификации данных дистанционного зондирования [19].

По результатам исследований С. Гавриленко, В. Челак и О. Хорносталь9 предложили два метода определения состояния вычислительной системы с использованием в качестве классификатора ансамбля деревьев решений на основе бустинга и бэггинга. Модификация применяемых классификаторов осуществлялась за счет задействования специальной процедуры выбора оптимальных параметров функционирования классификаторов, а также процедуры предобработки исходных данных.

В статье Г. Нго, Р. Бирда и Р. Чандры [20] представлено эволюционное обучение ансамблем с мешками деревьев, в котором эволюционные алгоритмы применяются для совершенствования содержимого мешков с целью итеративного улучшения ансамбля путем обеспечения разнообразия. Результаты показывают, что метод эволюционного ансамблевого бэггинга превосходит традиционные ансамблевые методы (бэггинг и случайные леса) для нескольких контрольных наборов данных при определенных ограничениях.

Тем не менее описанные методы и подходы пока не были реализованы для решения практической задачи, а именно для построения рейтинга регионов конкретно в разрезе отрасли радиоэлектронной промышленности.

МАТЕРИАЛЫ И МЕТОДЫ

Опишем этапы построения инновационного рейтинга регионов в РЭП с применением алгоритмов машинного обучения.

Этап 1 – предварительная разведка данных. Предполагает сбор необходимых данных по 83 регионам России за период 2010–2023 гг. на сайте Федеральной службы государственной статистики¹⁰. Выбор периода 2010–2023 гг. обусловлен отсутствием необходимых сведений за предыдущие годы.

Для моделирования использовались целевые функции (1: Объем инновационных товаров (всего); 2: Разработанные передовые производственные технологии (всего), ед.; 3: Сальдированный финансовый результат (информатизация и связь)), а также следующие входные переменные:

• 1    – Стоимость основных фондов (ОФ) (информатизация и связь);

• 2    – Ввод в действие ОФ (информатизация и связь);

• 3    – Оборот организаций (информатизация и связь);

• 4    – Затраты на внедрение и использование цифровых технологий (всего);

• 5    – Внутренние текущие затраты на научно-исследовательские работы (НИР) (фундаментальные исследования);

• 6    – Внутренние текущие затраты на НИР (прикладные исследования);

• 7    – Внутренние текущие затраты на НИР (разработки);

• 8    – Затраты на инновационную деятельность (всего);

• 9    – Используемые передовые производственные технологии (всего).

Таким образом собирались прямые и косвенные переменные, влияющие на инновационное развитие отрасли. К прямым переменным относились входы 1–3 и цель 3, к косвенным – все остальные. В итоге получилась матрица данных размерности 1162 х 13 .

Данные в рублях корректировались на инфляцию, т. е. вычислялись в ценах последнего в выбранном периоде, 2023, года. Для этого данные 2022 года умножались

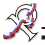
на сумму: 1 плюс ставка инфляция за 2023 год; данные 2021 года – сначала на сумму: 1 плюс ставка инфляции за 2022 год, затем – на 1 плюс ставка инфляции за 2023 год и т. д. Вся имеющаяся выборка разбивалась на выборку для обучения (2010-2022 гг., матрица данных размерности 1079 х 13 ) и выборку для верификации модели (2023 г., матрица данных размерности 83 х 13 ).

Поскольку распределения значений входных переменных в 2010–2022 гг. не подчиняются нормальному закону, их необходимо линеаризовать, т. е. вычислить натуральный логарифм. Однако, чтобы веса одних входных переменных в обучающейся модели не превалировали над другими, прежде следовало эти данные нормализовать по формуле:

^

X =

x x min

Y — Y ■ max   min где x - новое значение входной переменной; x - старое значение входной переменной.

Это было необходимо сделать, чтобы избавиться от отрицательных значений для последующей линеаризации данных.

Аналогично поступили с целевыми переменными. При этом нормализованные данные в виде нулей заменялись на 0,000001, чтобы провести их линеаризацию. Пропуски в данных отсутствовали.

Линеаризация используемых целевых функций необходима еще и для того, чтобы стало возможным присвоить регионам рейтинг, так как в случае линеаризации данные более растянуты вдоль горизонтальной оси и почти подчиняются нормальному закону распределения.

Для того чтобы параметры нормализации обучающей выборки не повлияли на результаты верификации обученной модели, следовало выборку для верификации (2023 г.) отдельно скорректировать согласно параметрам нормализации обучающей выборки.

Инновационный рейтинг в отрасли РЭП предполагает присвоение регионам страны следующих значений: ‘A’ – лидер; ‘B’ – со средним уровнем инновационного развития; ‘C’ – депрессивный.

При этом сегменты линеаризованных значений целевых функций выглядели так:

• 1)    цель 1 - 'A' с ( - 2; +да ), 'B' с ( - 5; - 2], 'C' с ( -да ; - 5];

• 2)    цель 2 - 'A' с ( - 2,5; +да ) , 'B' с ( - 8; - 2,5], 'C' с ( -^ ; - 8] ;

• 3)    цель 3 -'A' с ( - 2; +да ), 'B' : ( - 2,0845; - 2], 'C' с ( -да ; - 2,0845] .

Затем из значений для трех целевых функций формировался интегральный показатель “I-score”.

Этап 2 – машинное обучение модели различными методами на языке Python. Сначала из выборки для обучения случайным образом отбирались 20 % данных для тестирования модели, 15 % – для ее валидации. Кросс-валидация (перекрестная проверка) применялась для исключения эффекта переобучения. Параметр проверки по умолчанию – 5-кратная перекрестная проверка для защиты от переобучения.

С целью оценки качества обучения модели определялась ее точность ( accuracy ), а также использовались графики площади под кривой ошибок (ROC/AUC) и матрица ошибок ( confusion matrix ).

Предпочтительная точность модели приближена к 100 %. Соотношение между долей истинно положительных ( true positive rate, TPR ) и долей ложноположительных результатов (false positive rate, FPR ) показывает ROC-кривая. Для оценки производительности классификационных моделей часто задействуется такой показатель, как площадь под кривой ( area under the curve , AUC ). Чем он выше, тем ближе классификатор к идеальной модели. У модели, производящей случайный отбор, показатель AUC будет равен 0,5, у идеальной – 1.

Таким образом, в идеальном случае график ROC/AUC должен заполнять левый верхний угол; правильно классифицированные значения на матрице ошибок ( confusion matrix ) - должны находиться на главной диагонали, отклонения от нее показывают ошибки классификации.

Среди набора обучающих методов использовался и «случайный лес». Методология заключалась в создании ряда подвыборок или реплик бутстрапа из набора данных. Эти подвыборки генерировались случайным образом с заменой из списка значений в наборе данных. Для каждой реплики выращивалось дерево решений. Каждое дерево решений – само по себе обученный классификатор и для упорядочивания новых значений может привлекаться изолированно. Однако прогнозы двух деревьев, выращенных из двух разных реплик бутстрапа, могут быть различными.

Ансамбль объединяет прогнозы всех деревьев решений, выращенных для всех реплик бутстрапа. Если большинство деревьев предсказывают один конкретный класс для нового значения, разумно считать, что этот прогноз более надежный, чем прогноз любого отдельного дерева. Если другой класс предсказывается меньшим набором деревьев, эта информация также полезна. Фактически доля деревьев, прогнозирующих различные классы, является основой для оценок классификации, которые сообщает ансамбль при классификации новых данных.

Этап 3 – тестирование обученной модели. Описанный подход позволил оптимально настроить гиперпараметры обучаемой модели, в числе которых варьируется набор предикторов (входных переменных). Это дало возможность сравнить результаты моделей, обученных на предыдущем этапе. Нередко оптимизированные ансамбли по точности на тестовых данных превосходят как обычный «случайный лес», так и другие модели машинного обучения.

Этап 4 – верификация обученной модели. Проводился на новых, совершенно не знакомых обученной модели данных 2023 года. Для этого прогнозируемые на ее основе инновационные рейтинги (I-score) сравнивались с фактическими (2023 г.). Точность верификации оценивалась для 83 исследуемых регионов России; желательной считалась близкая к 100 %.

Этап 5 – построение карты инновационного рейтинга регионов. Подобная географической карта позволяет наглядно позиционировать регионы как лидеров (рейтинг ‘A’), со средним уровнем инновационного развития (‘B’) и депрессивные (рейтинг ‘C’), а также сравнить прогнозируемые и фактические значения инновационного рейтинга регионов в отрасли РЭП в 2023 г.

Полезна информация и о несоответствии предсказанных по модели рейтингов фактическим. Это может свидетельствовать о возможности будущего изменения рейтингов регионов.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

Апробация разработанной модели на данных за 2010–2022 гг. позволила построить инновационный рейтинг регионов России в отрасли РЭП с применением метода решающих деревьев согласно описанному алгоритму, а также оценить точность прогноза.

Этап 1. По итогам предварительной разведки данных за 2010–2022 гг. была получена матрица (табл. 1), где первые значения – сырые данные, вторые – обработанные, т. е. нормализованные и линеаризованные.

Т а б л и ц а 1. Матрица подготовленных для анализа сырых и обработанных данных ¹¹

T a b l e 1. Matrix of raw and processed data prepared for analysis

Параметр, млн руб. / Parameter, million rubles	Регионы / Regions
	1. Белгородская область / 1. Belgorod Region	2. Брянская область / 2. Bryansk Region		83. Чукотский автономный округ / 83. Chukotka Autonomous Area
1	2	3	4	5
2010 год / 2010 year
Вход 1 – Стоимость ОФ (информатизация и связь) / Input 1 – Cost of the fixed assets (informatization and communication)	6697,58673 – 0,297227	13440,3146 – 0,237707		664,188752 – 0,350486
Вход 2 – Ввод в действие ОФ (информатизация и связь) / Input 2 – Commissioning of the fixed assets (informatization and communicaion)	415,728263 – 0,249949	1031,9365 – 0,20453		776,075318 – 0,223389
Вход 3 – Оборот организаций (информатизация и связь), млрд руб. / Input 3 – Turnover of organizations (informatization and communication), billion rubles	2,18790219 – 0,149277	9,36936937 – 0,101282		0,566280566 – 0,160114
Вход 4 – Затраты на внедрение и использование цифровых технологий (всего) / Input 4 – Costs of implementation and use of digital technologies (total)	3276,2 – 0,132452	1856,4 – 0,153537		970 – 0,166701
Вход 5 – Внутренние текущие затраты на НИР (фундаментальные исследования) / Input 5 – Internal current costs of research and development (fundamental research)	185,8 – 0,217468	48,1 – 0,247854		0 – 0,258469
Вход 6 – Внутренние текущие затраты на НИР (прикладные исследования) / Input 6 – Internal current costs of research and development	301,5 – 0,184358	38,6 – 0,230581		0 – 0,237367

(applied research)

Окончание табл. 1 / End of table 1

1	2	3	4	5
Вход 7 – Внутренние текущие затраты на НИР (разработки) / Input 7 – Internal current R and D costs (development)	388,9 – 0,268912	115,4 – 0,287534		32,1 – 0,293206
Вход 8 – Затраты на инновационную деятельность (все-	3072,3	929,7		14,2
го) / Input 8 – Costs of innovation activities (total)	– 0,291664	– 0,372249		– 0,406681
Вход 9 – Используемые передовые производственные	1215	1021		0
технологии (всего), ед. / Input 9 – Used advanced produc-	– 0,457077	– 0,515244		– 0,821368
tion technologies (total), units Цель 1: Объем инновационных товаров (всего) / Target	9391,6	4434,4		186,9
1: Volume of innovative goods (total)	– 4,107719	– 4,858143		– 8,024716
Рейтинги: / Ratings: 'A' с ( - 2; +® ), 'B' a ( - 5; - 2], 'C' с ( -да ; - 5].	‘B’	‘B’		‘C’
Цель 2: Разработанные передовые производственные технологии (всего), ед. / Tar-	10	5		0
get 2: Developed advanced manufacturing technologies (total), units	– 4,039536	– 4,732684		– 13,815511
Рейтинги: / Ratings: 'A' c ( - 2,5; +да ) , 'B' a ( - 8; - 2,5], 'C' с ( -да ; - 8] .	‘B’	‘B’		‘C’
Цель 3: Сальдированный финансовый результат (информатизация и связь) / Tar-	1043	0		68
get 3: Balanced financial result (information and communication)	– 2,056571	– 2,084786		– 2,082922
Рейтинги: / Ratings: 'A' c ( - 2; +да ), 'B' о ( - 2,0845; - 2], 'C' с ( -да ; - 2,0845] .	‘B’	‘C’		‘B’
Рейтинг I-score / Rating I-score	‘B’	‘B’		‘C’

Предварительный анализ данных показал наличие тесной положительной корреляции между выбранными входными переменными 1–9 и целевыми функциями 1–3. Это подтвердило обоснованность выбора именно таких входных переменных и целевых функций.

Этап 2. В актуальной задаче классификации для трех целевых функций получились разные наилучшие модели машинного обучения на тесте (табл. 2).

Т а б л и ц а 2. Наиболее качественные обученные модели

T a b l e 2. Best trained models

Характеристика модели / Model Characteristics	Цель 1 / Target 1	Цель 2 / Target 2	Цель 3 / Target 3	I-score (интегральный показатель на основе трех целевых функций / integral indicator based on three objective functions)
Лучшая модель /	Random	Bagged	Random	Fine Gaussian SVM
Best Model	Forrest	Trees	Forrest
Точность на тесте / Test Accuracy Точность на	0,8100	0,8148	0,6000	0,8660
верификации / Verification	0,8795	0,6867	0,7953	0,8193
Accuracy

При обучении сразу I-score на выборке 2010–2022 гг. была получена наилучшая модель «точный гауссовский SVM».

Этап 3. Матрица ошибок, представленная на рисунке 1, показывает, что модель, обученная для интегрального показателя I-score, на тесте неправильно определила лишь 13,3 % регионов класса ‘A’ (2 : (13 + 2) 100 %), 5,6 % – класса ‘B’ (7 : (119 + 7) 100 %) и 26,7 % регионов класса ‘C’ (20 : (55 + 20) 100 %). При этом F1-score (мера производительности модели, которая объединяет точность и полноту в единую метрику в диапазоне от 0 до 1, т. е. служит гармоническим средним точности и полноты) равен 0,83. Это достаточно качественный результат.

Р и с. 1. Матрица ошибок на тесте для модели Fine Gaussian SVM, обученной для интегрального показателя I-score

F i g. 1. Test confusion matrix for a model Fine Gaussian SVM trained for the integral I-score metric

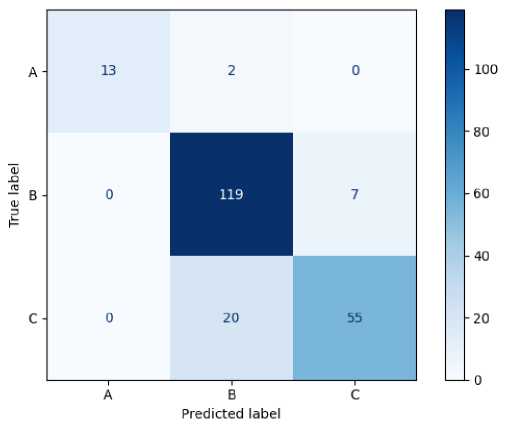
Графики ROC/AUC продемонстрировали достаточно качественные результаты на тесте для всех трех рейтингов (рис. 2). Средний ROC/AUC составил 0,94.

Р и с. 2. Графики ROC/AUC на тесте для модели, обученной для интегрального показателя I-score

F i g. 2. ROC/AUC schedules for a model trained for the integral I-score metric

Этап 4. В ходе верификации обученные модели также обнаружили высокую точность (см. табл. 2). При этом на новых, не знакомых модели, данных (2023 г.) точность верификации для I-score достигла 81,93 %.

Матрица ошибок показала, что модель, обученная для I-score, на верификации неправильно определяет 50 % регионов класса ‘A’, 11,9 – класса ‘B’ и 21,9 % регионов класса ‘C’. Это достаточно качественный результат.

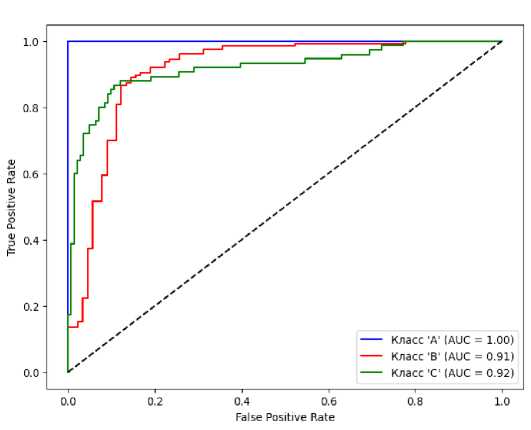
Этап 5. Согласно географической карте инновационного рейтинга регионов России (I-score) (рис. 3) в отрасли РЭП в 2023 г. регионами – лидерами (рейтинг ‘A’) стали Московская область, города Москва и Санкт-Петербург, Республика Татарстан, Нижегородская и Свердловская области.

ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ

На языке Python написана программа, позволяющая построить карту инновационного рейтинга регионов в отрасли РЭП и для этого использующая различные алгоритмы машинного обучения: «случайный лес» ( Random Forrest ), подпространство k ближайших соседей ( Subspace KNN ), мешок деревьев ( Bagged Trees ), точную гауссову машину опорных векторов ( Fine Gaussian SVM ).

Обучающая выборка формировалась по данным Росстата за 2010–2022 гг., а именно по 83 регионам России. Апробация разработанной модели осуществлялась на базе независимых данных (за 2023 г.), которые не входили в обучающую выборку. Верификация подтвердила практическую применимость модели: точность прогноза интегрального показателя I-score на новых данных составила 81,93 %.

Регионам страны присваивались следующие значения инновационного рейтинга в отрасли РЭП: 1) ‘A’ – лидер; 2) ‘B’ – со средним уровнем инновационного развития; 3) ‘C’ – депрессивный. Затем из значений для трех целевых функций формировался итоговый интегральный показатель “I-score”.

Согласно карте инновационного рейтинга регионов России (см. табл. 3), в радиоэлектронной промышленности в 2023 г. регионами-лидерами (рейтинг ‘A’) стали Московская область, города Москва и Санкт-Петербург, Республика Татарстан, Нижегородская и Свердловская области.

Обученная модель спрогнозировала, что Новосибирская область также в 2023 г. попадает в число регионов-лидеров (рейтинг ‘A’). Хотя на практике этого не произошло, тем не менее подобный прогноз свидетельствует о том, что у Новосибирской области есть реальные перспективы в ближайшем будущем попасть в число регионов – лидеров в отрасли развития радиоэлектронной промышленности.

Республика Башкортостан, Пермский край и Челябинская область, напротив, по факту в 2023 г. попали в число лидеров (рейтинг ‘A’), однако обученная модель спрогнозировала для них рейтинг ‘B’ (регионы со средним уровнем инновационного развития). Это можно расценивать как погрешность модели либо как вероятность потери лидирующих позиций в отрасли РЭП для этих территорий в будущем.

Полученные результаты будут полезны государственным структурам и производственным компаниям для планирования инновационного развития отрасли радиоэлектронной промышленности.

Перспективы исследования связаны с применением карт Кохонена для определения статистических групп рейтингов с последующим машинным обучением для задачи классификации; глубокого обучения для задачи классификации с использованием сети долговременной краткосрочной памяти (Long Short-Term Memory). Ограничением исследования может быть недостаточная прямая корреляция входных переменных модели с целевыми функциями.