Инструментально-вероятностный метод оптимизации поиска отказа в радиоэлектронном оборудовании

Поиск места отказа в современной радиоэлектронной системе представляет сложную техническую задачу. Как правило, основное количество времени при ремонте радиооборудования затрачивается именно на поиск отказа (примерно до 70…80%). Поэтому вполне естественно, что методам рационального решения данной задачи уделяется так много внимания. В общем случае методы поиска отказа можно разделить на вероятностные и инструментальные методы, причем часто это разделение условное.

Несмотря на большое разнообразие методов оптимизированного поиска отказа в этой области много не проработанных мест, в частности нет четкого и однозначного критерия, определяющего эффективность метода, и общей теоретической основы.

В настоящей статье производится попытка дать обобщающую теоретическую основу для инструментальных методов поиска места отказа, к которым относятся методы последовательных и групповых измерений, из которых наиболее известен метод половинного разбиения (метод средней точки, дихотомический метод). Отличительной особенностью инструментальных методов поиска является то, что они гарантированно снижают среднее или абсолютное количество измерений, что создает преимущества при их использовании вместо вероятностных методов поиска (учитывающих вероятности отказов элементов). Перспективным представляется совмещение методов обоих типов.

При методе половинного разбиения, являющимся одним из наиболее эффективных методов групповых измерений, абсолютное количество измерений необходимое для точного определения места отказа определяется выражением n = log2 N (1)

где N - общее количество элементов входящих в систему.

Несмотря на значительные преимущества данного метода, имеется возможность дальнейшего улучшения эффективности алгоритмов подобного типа.

Для исследования данной проблемы проанализируем модель поиска места отказа в радиоэлектронной системе, при этом рассмотрим наиболее простой случай - когда радиоэлектронная система состоит из последовательно соединенных функциональных блоков. Структура такого типа является наиболее распространенной и применяется чаще, чем структура параллельного. Будем проводить поиск отказа методом групповых измерений (измерять групповой сигнал части системы). Выберем произвольную точку в схеме, которая будет разбивать систему на М и N - M блоков. В этом случае можно сказать, что система разбивается в пропорции ( 0,5 + k )/( 0,5 - k ) , где k -отклонение от середины.

Несложно определить каково будет максимальное и минимальное количество измерений необходимых для выявления отказа, сложнее определить среднее их количество.

Выясним, сколько элементов остается непроверенными после каждой проверки. После первого измерения можно выявить работоспособность части системы, причем может быть два случая - когда неисправность оказалась в части системы включающей М блоков и когда неисправность находится в части системы с N - М блоками, то есть тх =(0,5 - к )• N; m1 =(0,5 + к )• N здесь N - общее количество элементов системы; k - отклонение пропорции от середины.

Продолжая рассуждать аналогичным образом, можно было бы в конечном итоге определить среднее количество измерений, но можно пойти более простым путем. Среднее количество измерений определим, исходя из соображений, что отказ может оказаться в любой из частей, и в среднем будет равное количество сомножителей (0,5 - к) и (0,5 + к), и после проведения оче- редного измерения количество непроверенных элементов m0 = (о,25 — к2 )2 • N

где n – номер проводимого измерения.

Очевидно, что в конце поиска остается один непроверенный элемент т.е. m₀ = 1 .

Таким образом, среднее количество измерений составит n0 = logo,25-^2 N-2 = — log2 n/l°g2 V(°’25 - k2) = -2^ N^^ - k2)        (3)

Наихудший случай будет, когда отказ постоянно оказывается в большей части и m0 = (0,5 + к)n • N = 1, что соответствует количеству измерений nmax = log°,5+k (1 N)= log2 N/log2 1 (°,5 + k)]                      (4)

Если отказ оказывается всегда в меньшей части, то количество элементов m0 = (0,5 — к)n • N = 1. Число измерений при этом будет минимальным и со- ставит nmin = l0g°,5—k (1 N) = log2 N/l°g2 [V(°’5 — k)]

Как видно из выражения (3), среднее количество измерений начинает падать, однако делать выводы еще рано, так как необходимо учесть, что вероятность обнаружения отказа будет наибольшей на большем участке. Раз- вивая далее эту идею далее можно легко показать, что в среднем количество сомножителей (°,5 + k) и (°,5 — k) будет находиться в соотношении (0,5 + к )/(0,5—к), тогда справедливо будет выражение m0 = (0,5 + к)(0,5+к)n (0,5 — к)(0,5—к)n • N (6)

Из (6) определим, что среднее количество измерений составит ln N

n ° = — ( °,5 + k ) ln ( °,5 + k ) + ( °,5 — k ) ln ( °,5 — k )

То есть, с ростом отклонения пропорции разбиения от середины количество измерений будет увеличиваться, что вполне соответствует действи- тельности.

Определим частную производную от среднего количества измерений по k dn 0 =__________[ln (0,5 + к)—ln (0,5 — к)]_________ln N                   (8)

d к   [ ( 0,5 + к ) ln ( 0,5 + к ) + ( 0,5 — к ) ln ( 0,5 — к ) ] ²

Частная производная (8) показывает, как изменяется среднее количества измерений (7) в зависимости от пропорции разбиения. Анализируя приведенные выше выражения можно сформулировать критерий оптимального поиска отказа в виде

R = n ₀ — dn₀ /дк ^ 0

Графики, поясняющие сущность заданного критерия (9), представлены на рис.1.

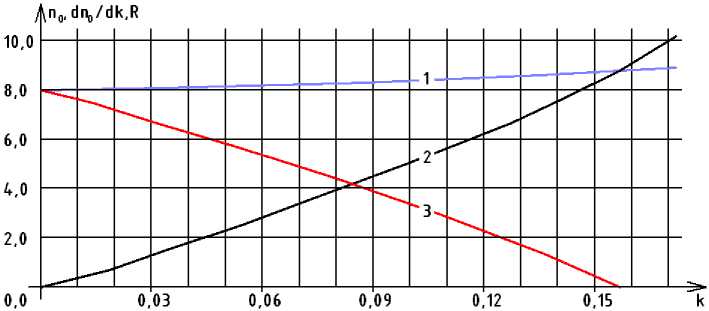
Рис.1. Графики зависимостей среднего количества измерений (1), скорости приращения количества измерений (2), критерия поиска отказа (3) от отклонения пропорции разбиения от значения 0,5.

Наглядно понятие скорости приращений количества измерений можно уяснить из рис.2, на котором показаны зависимости среднего количества измерений от числа элементов системы при различных значениях пропорции. Из представленного графика видно, что среднее количество измерений с ростом отклонения начинает резко возрастать, что приводит к снижению эффективности поиска и увеличивает время его проведения.

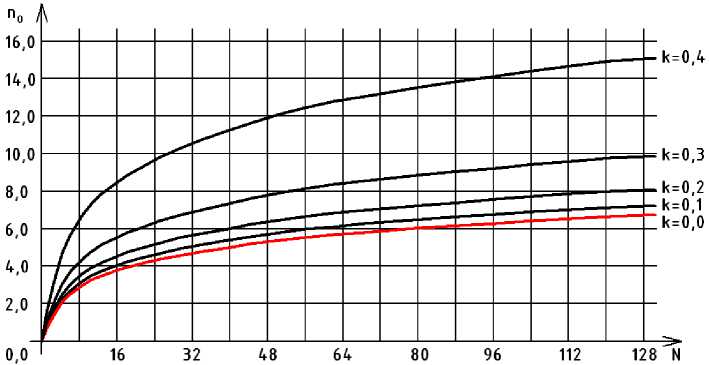
Рис.2. Зависимость среднего количества измерения от числа элементов системы при различных пропорциях ее разбиения.

Основным достоинством рассматриваемого метода является то, что его можно комбинировать с методом время-вероятность, что сдвигает среднее количество измерений в сторону уменьшения, так как учет вероятности отказов блоков не только компенсирует степени в выражении (6) и среднее количество измерений будет находиться в пределах определяемых выражениями (5) и (7). Из сказанного выше следует, что предлагаемый метод по эффектив- ности превосходит существующие и может легко применяться в автоматических системах технической диагностики для повышения их эффективности.