Интеграция инерциальной, спутниковой и астроинформации в задаче коррекции навигационной системы

Как известно [1], автономные инерциальные навигационные системы (ИНС) предназначены для определения параметров местоположения и пространственной ориентации подвижных объектов, но неустойчивость таких систем является заметным препятствием для их широкого применения. Получившие в настоящее время распространение навига-

• ¹    © Числов К. А., 2012

Исследование выполнено при поддержке РФФИ-ДВО (грант № 11-01-98501-р_восток_а) и ДВО РАН (грант № 12-1-0-03-005).

ционные спутниковые системы (НСС), например, типа ГЛОНАСС, вообще говоря, способны решать те же задачи, что и ИНС, но для решения второй из них (задачи ориентации) на борту объекта необходимо создать сеть пространственно разнесённых приёмников сигналов НСС [2]. Вместе с тем требования к сети, обусловливаемые требованиями к точности и надёжности решения задачи, далеко не всегда совместимы с возможностями их удовлетворения на подвижном объекте.

Объединение (интеграция) типа ИНС-НСС обеих систем в рамках концепции задачи коррекции ИНС при одном приёмнике НСС на борту объекта в принципе позволяет, как показано в этой статье ниже, устойчиво решать обе упомянутые выше навигационные задачи. Вместе с такой интегрированной системой исследуется навигационная система более высокой степени интеграции (типа ИНС-НСС-АС), включающая в свой состав наряду с ИНС и НСС астросистему (АС), причём к последней предъявляется в определённом смысле минимальное требование – обеспечение задачи коррекции ИНС угломерной информацией при наблюдении одной звезды. Такое дополнительное комплексиро-вание навигационной информации в рассматриваемом случае, когда задача определения места объекта, по существу, может быть качественно решена НСС, направлено не только на улучшение разрешимости задачи навигации в целом, но прежде всего её части, относящейся к задаче ориентации, качественное и надёжное решение которой приобретает особое значение, если подвижный объект является носителем информационных и силовых платформ.

Основные модельные представления

Переходя к формальным описаниям, отметим, что базовая модель метода инерциальной навигации (ИНМ) представляется двумя группами дифференциальных уравнений – динамической (ДГУ) и кинематической (КГУ) [1], где первая описывает траекторию, а вторая – эволюцию системы отсчёта, в которой траектория рассматривается. Тогда идеализированная модель обратной задачи, решаемой в рамках метода, может быть записана в следующем общем виде:

Dq = p , q ⁽⁰⁾ = q o ,

Dp = G + F , p (0) = p o ,

DA = 0, A(0) = Ao, z = J(q, p, A), где векторные переменные – q (радиус-вектор места носителя), p (удельный импульс, или, что то же самое, абсолютная линейная скорость носителя), G (напряженность GE-поля), F (удельная сила негравитационной природы) - записываются в проекциях на оси вращающейся с абсолютной угловой скоростью w = (Wj, ш2, ш3)Т правой ортогональной системы отсчёта 0q = 0q 1 q2q3 с началом в центре масс Земли, осью 0q3, направленной по радиус-вектору местоположения носителя, и осями 0q 1 и 0q2, направленными соответственно на географические Восток и Север; т - символ транспонирования векторов и матриц; A = (Aj) - матрица ориентации приборной системы отсчёта относительно выбранной инерциальной, (i, j) = 1,3 ; z - вектор измерений (дополнительных к инерциальным), доставляемых от НСС и астросистемы; J(q, p, A) -    51

функция связи «состояние-измерение»;

I) = d dr + co - оператор абсолютной производной; – кососимметрическая матрица, составленная из компоне нт вектора ω так, ^что ^^dk/'H, ( i , k , j ) = 1,3 ; eikj ^- опера тор Леви-Чивиты; инерциальные измерения значений компонент векторов w и F выполняются в приборной системе отсчёта с осями, параллельными соответствующим осям системы 0 q .

Далее с учётом физических реальностей, а это – наличие погрешностей в измерениях, в определении начальных значений q ₀ и p ₀, а также неполнота представлений о GE-поле (то есть о векторе G ( q, r ), r = | q |), осуществим переход от уравнений (1) к линейным уравнениям в вариациях. В итоге получим

D5q = op- vq, oq(0) = 5q0,

Dop = G^Sq + g + f- vp + G; e3, 5p(0) = 5p0, g = zM, g(O) = go,

Dp = v, p(O) = po,

^i =

IIHC - Фнсс ⁼ -^-Pi + ^£i’            

⁽²⁾

Г

Os₂ = (a_iihc — Х_нсс)СО8ф = — —-— p₂ + ^e2’ Г

З-з = 7imc "" 7нсс = ^з + £3’

• 6 - _? — e^jl]^ j + £₃ , 5 — 4, 5.

где v и f - векторы инструментальных погрешностей гироскопов и ньютонометров; φ, λ и r – соответственно геоцентрические широта, долгота и радиус места объекта-носителя, вычисляемые ИНС (ф ИНС , Х ИНС , r ИНС ) и доставляемые НСС (ф_НСС, Х Н _СС, r _НСС); е,, i = 1,3 , - вектор инструментальных погрешностей НСС-определений; в = (в i ), i = 1,3, -вектор погрешностей интегрирования КГУ;

l = ( l_рl ₂, 1 ₃)^T - орт визирования звезды в проекциях на оси приборного координатного трёх-

ИССЛЕДОВАНИЯ

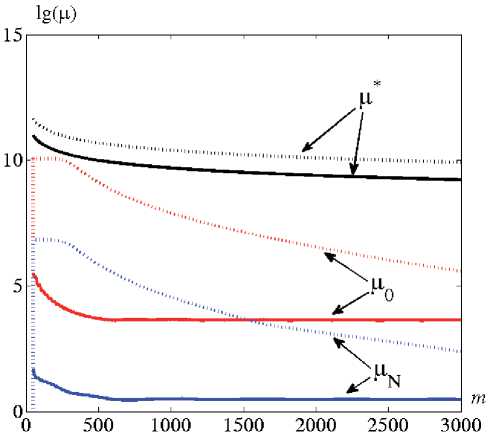
HAVKO____________ Ж ГРАДА гранника; £$. 5 = 4,5 - инструментальные погрешности визирования звезды; 8z = (Sz, ^ -вектор невязок измерений, причём κ = 3 для системы ИНС-СНС и κ = 5 для системы ИНС-НСС-АС; Sq и Sp - погрешности интегрирования ДГУ; G q = dG / dq и G r = dG / dr, в частности, при центральности GE-поля (именно для этого случая ниже будут представлены результаты вычислительного эксперимента) g:,=-

Цель решения задачи (2) – это оценки 8q*, 8p*, в* векторов 8q, Sp, в и в конечном итоге оценки векторов q, p, и матрицы А, образуемые следующим образом: q* = q + ~q*, p* = ~ + 8p*, A = (E + M, где q , p и A -результаты интегрирования ДГУ и КГУ, или модельные значения, Е – единичная матрица.

В модели (2) дополнительного разъяснения требуют два последних уравнения, характеризующие астроинформацию.

Пусть L – орт направления на звезду в инерциальной системе отсчёта, тогда l = AL -орт этой же звезды в приборном трёхграннике. Числовым же образом l в этом трёхграннике является вектор 1 = AL = (1- /М, так что методологическая часть погрешности визирования звезды в нём есть Al = l -1 = l р. Перейдём к модели инструментальной погрешности. Обозначим через Y1 и Y₂ «азимутальный» и «высотный» углы положения звезды в приборном трёхграннике, а через А1 и А₂ - соответственно инструментальные погрешности измерений этих углов при наблюдении звезды. Тогда в (2) t_s = g_yA_r g_y = cl, m_;, где с учётом индексации инструментальных погрешностей НСС можно было бы принять s = 4,6, j = 1,2. Вместе с тем, принимая во внимание линейную зависимость строк матрицыl , можем ограничиться значениями s = 4,5 и представить вектор невязок астроизмерений в виде Azs=Аls + £s, s = 4,5, что и отражено в модели (2). В общем случае l = l(t), в частном -при движении объекта вдоль параллели (в северном полушарии Земли), когда доступна наблюдению Полярная звезда l = (0, cos ф, sin ф)^т (именно для такого случая в этой статье представлены вычислительные эксперименты).

Модель (2) представляет собой систему уравнений «состояние-измерение»[3], и зада-

№ 2 (2) апрель-июнь 2012

ча может быть решена непосредственно, если обратиться к методу динамического обращения, реализовав его, например, с помощью алгоритма калмановского типа [4]. Наряду с этим, учитывая линейность уравнений, модель задачи весьма стандартным способом может быть приведена к системе линейных алгебраических уравнений с некоторым конечномерным оператором (матрицей) L размерности ктхn (dim L = ктхn), динамически расширяемым по m по мере накопления измерений, и n = dim(δq^T, δp^T, β^T); в этом случае решение задачи интерпретируется в рамках представлений метода наименьших квадратов (МНК/LSM).

Вычислительные эксперименты

Основная цель выполненных экспериментов - верификация корректности математической постановки задачи в условиях конечной точности вычислений и измерений; достигается она при исследовании на невырожденность матрицы L (её можно отождествлять с матрицей наблюдаемости [4]) и при непосредственном построении решения с использованием алгоритма динамического обращения Калмана [3, 4].

Упоминаемая здесь матрица L имеет вид L = (НФ(г₀. т, ))"=„, т - целое число, причём m > n; t = mh; h - шаг дискретизации задачи по времени t, dim L = кт хn; Н - матрица связи «состояние-измерение», так что 8z = Hx + £, dim Н = кхn; Ф(1₀, t) - фундаментальная матрица решения однородного дифференциального уравнения, соответствующего дифференциальному уравнению в модели (2), dim Ф(t0, t .) = n хn.

На рис. 1 приводятся графики (сплошные линии – для систем типа ИНС-НСС-АС, прерывистые – для ИНС-НСС) значений сингулярных чисел обусловленности р₀, рN и р*, где р₀ и рN - вычисленные при относительной машинной (компьютерной) точности вычислений e 1 = 2,2А0^-16 числа обусловленности соответственно исходной (L) и нормированной по столбцам (N = LD^-1) матриц; D = ^diag^(||Li^{|1, ||L}2^||,^^,||LnИ), ||L.|| -евклидова норма i-го столбца матрицы L;

– критическое число обусловленности [5].

Условие разрешимости задачи (2) в вычислительной среде, а именно: р* > р₀ и/или p^* > p_N, что хорошо видно из рис. 1, выполняется для обоих типов систем. Последнее

Таблица 1

g = 10-5 м/с2 g = 10-4 м/с2 g = 10-3 м/с2 1 Ав,| 7,31·10-8 7,41·10-8 7,42·10-8 4,22·10-7 4,72·10-7 8,91·10-7 1 Ав21 3,71·10-7 3,80·10-7 7,25·10-7 5,25·10-7 7,62·10-7 9,36·10-7 1 Авз1 3,68·10-7 3,75·10-7 6,89·10-7 4,27·10-7 4,88·10-7 8,84·10-7 |AaJ 1,16·10-7 1,16·10-7 1,19·10-7 4,12·10-7 4,69·10-7 8,89·10-7 |Аа2 3,67·10-7 3,76·10-7 7,24·10-7 5,27·10-7 6,83·10-7 9,43·10-7 означает сходимость (по m) алгоритмов МНК и асимптотическую устойчивость (по t) алгоритмов динамического обращения калма-новского типа. Отметим, что графики рис. 1 построены для случая движения объекта по географической параллели ф = 45° в восточном направлении с относительной (к Земле) скоростью V = 100 м/с, h = 1 с; однако вывод о разрешимости задачи сохраняется и для других значений φ и V.

В таблице представлены наибольшие абсолютные значения погрешностей оценивания соответствующих переменных (где |Аа_i| = |Аq.|/r, i = 1,2) за пределами первой 1000 с. решения задачи для обоих типов систем (верхние строки – для системы ИНС-НСС-АС, нижние – для ИНС-НСС) при среднеквадратических значениях компонент погрешностей измерений ε, f, ν, соответственно равных гт, =1м, i = 1,3; <т^=1(г° рад, i = 4,5 g _t = ЦГ³ м с², i = 1,3; g_Vi = КГ^ град час, i = 1,3 , и при различных представлениях о модели напряженности GE-поля для случаев g = |g| = const.

Как видно из результатов вычислительных экспериментов, имеет место весьма несущественное качественное различие исследованных двух типов интегрированных систем.

Выполненное исследование указывает на достаточно высокую эффективность и перспективность рассмотренных типов интегрированных систем для решения задач построения информационных и силовых платформ для подвижных объектов широкого профиля назначения.

Автор благодарит доктора технических наук, главного научного сотрудника, заведующего Сектором управления и навигации ИАПУ ДВО РАН профессора А. С. Девятисильного за помощь в работе над статьёй.

Рис. 1. Графики значений чисел обусловленности