Интеграция нечетких моделей для анализа временных рядов

ний о тенденциях во временных рядах трудоемка и дорогостояща.

Поэтому при создании нечетких моделей ВР перспективным является применение интеллектуальных методов направления Times-Series Data Mining , в котором нечеткое моделирование ВР позволяет извлекать дополнительные знания в виде легко интерпретируемых продукционных правил. Нечеткое моделирование и представление ВР в виде нечеткого временного ряда (НВР) активно развивается в трудах иностранных ученых, таких как Х. Танака, Келминс и Диамонд, К.Сонг, К. Хирота, Я. Капржик, В. Педрич, В. Новак, И.Перфильева, И. Батыршин, а также в работах отечественных ученых – Н. Ярушкиной, С. Ковалева, К.Дегтярева. Несмотря на перечисленные работы, ряд научных проблем нечеткого моделирования ВР в новом направлении Times-Series Data Mining остаются нерешенными, в частности проблемы моделирования, анализа и прогноза развития такого объекта временного ряда, как нечеткая тенденция.

Здесь для постановки задачи исследований выбран временной ряд в виде последовательности упорядоченных в моменты времени пар Y= { t _i ,x_i }, таких что x _{i ∈} В , t _i ∈ Вt, i ∈ [1,n] . Требуется построить нечеткую модель временного ряда, позволяющую извлекать знания о тенденциях и правилах их следования, образующую базу знаний Rule={R _k ^p }, где k – количество нечетких продукционных правил в базе знаний, p – количество переменных (нечетких высказываний) в каждом правиле:

R ip : Если x , есть ~ , и x есть xj и ... x_p есть ~_p то y есть ~ i .

Метод нечеткого моделирования заключается в построении для исследуемого ВР контекстно-зависимой параметрической ACL-шкалы [1], генерации базы знаний нечеткой модели ВР, со- держащей отношения между нечеткими элементарными тенденциями [2] временного ряда, и поиск такого параметра р базы правил Rule={R kp }, для которого ошибка прогноза минимальна.

В основу моделирования поведения ВР в терминах нечетких тенденций положим предположение о развитии поведения ВР как результата зависимости нечеткой тенденции от значений нечетких тенденций в предыдущие моменты времени.

Предлагаются три нечеткие модели временного ряда, выражающие эту зависимость через компоненты модели элементарной нечеткой тенденции. Результатами прогноза ВР являются параметры нечеткой элементарной тенденции τ , выражающие тип v ~ , интенсивность a ~ , степень принадлежности μ будущих изменений и числовая оценки уровней ВР, полученные по наилучшей модели.

В основе нечеткой модели временного ряда F2S лежит нечеткая модель элементарной тенденции τ =(μ, v ~ , a ~ ) , Тогда нечеткая модель ВР порядка р , выраженная через компоненты модели элементарной тенденции представима следующим образом:

ν ~( t - р ) o R _ν ~ ( t , t - р ) → ν ~ ( t ) ,

α ~( t - р ) o R _α ~ ( t , t - р ) → α ~ ( t ) .

Результатом моделирования ВР является база правил {R(t,t-р)} нечеткой системы логического вывода, выявляющая нечеткую зависимость следования отдельных компонент модели элементарной тенденции, извлеченная из нечеткого ВР, пример которой с частотной характеристикой каждого правила для р=1 представлен в табл. 1.

Данная модель временного ряда F1N основана на представлении временного ряда в виде числового ВР дефазифицированных интенсивностей нечеткой элементарной тенденции:

τ =(μ,н, α ) , н= DeFuzzy( v ~ ), α =DeFuzzy( a ~ ).

Для прогнозирования значений этого ряда удобно использовать трехслойную нейросетевую модель, с количеством входов, равным порядку модели р и одним выходом:

р α′=F(∑wiαi), i =1

где (α1,α2,...,αр)T – вектор входных интенсивностей, (w1,w2,...,wр) – вектор весовых коэффи- циентов, F – оператор нелинейного преобразования, неявно выражающий зависимость выхода от входа.

Модель F3N1S использует представление нечеткой элементарной тенденции в виде         τ

=( a ~ ,μ₁, μ₂,μ₃), где μ₁, μ₂, μ₃ – числовые временные ряды степеней принадлежностей (функции принадлежностей) типов элементарных тенденций:

α ~( t - р ) o R _α ~ ( t , t - р ) → α ~ ( t )

р р

µ ₁ ′ = F ₁ ( ∑ w_i µ _{1 i} ) , µ ₂ ′ = F ₂ ( ∑ w_i µ _{2 i} ) , i = 1                                                  i = 1

р

^µ 3 ^{′ =} F 3 ( ∑ w i ^µ 3 i ) , r = arg(max( µ ₁ ′ , µ ₂ ′ , µ ′ ₃), i = 1

где r – номер типа тенденции.

Далее проводится вычислительный эксперимент, целью которого является исследование продуктивности метода нечеткого моделирования ВР для генерации авторских моделей временных рядов, позволяющих извлекать знания о нечетких тенденциях в форме продукционных правил “IF-THEN” и использовать их для прогнозирования ВР.

Для выбора наилучшей из трех предлагаемых нечетких моделей ВР в терминах нечетких тенденций используются следующие критерии качества:

N

МАРЕ =

N ^∑ t = 1

yt

⋅ 100%

,

MSE = ¹ ∑ ⁿ ( y i - y t ⁰ ) ² , n i = 1

TTend = (ErrorCount / TotalCount) * 100% .

МАРЕ – средняя абсолютная процентная ошибка. Данный критерий удобно использовать для сравнения продуктивности метода при его применении на множестве временных рядов.

MSE – средняя квадратичная ошибка, традиционно используется для выбора наилучшей модели временных рядов из множества конкурирующих. Иногда применяют корень квадратный из MSE. Такой показатель качества обозначают RMSE.

TTend – коэффициент ошибок в обнаружении типов нечетких элементарных тенденций вре-

Таблица 1. Таблица извлеченных правил для типов тенденций

Правило Частота if ((Input0 is Падение)) then (Output is Рост) 3 if ((Input0 is Рост)) then (Output is Рост) 1 if ((Input0 is Рост)) then (Output is Падение) 2 if ((Input0 is Падение)) then (Output is Падение) 2 менного ряда в процентах, где ErrorCount – количество ошибок в моделировании типов нечетких элементарных тенденций, TotalCount – общее количество нечетких элементарных тенденции временного ряда.

Вычислительный эксперимент на нестационарных временных рядах показал, что авторские нечеткие модели ВР в терминах нечетких тенденций имеют недостаточно хорошие показатели качества для среднесрочного и долгосрочного прогноза за счет обработки “сырых данных” без выделения тренда. В то же время для краткосрочного прогноза авторские модели показали неплохие результаты, как по критериям качества моделирования и оценки прогноза нечетких тенденций, так и для оценки числовых уровней ВР.

В эксперименте были использованы авторские нечеткие модели тенденций F2S(Х,Y,Z), F1N(Х,Y,Z), F3N1S(Х,Y,Z) и для сравнения нечеткие модели S(Х,Y,Z) [3], D(Х,Y,Z) [4]. В этих моделях Х обозначает мощность генерируемой ACL-шкалы, Y – порядок модели, Z – глубина прогноза (количество интервалов для прогноза). В некоторых моделях будет использоваться авторский алгоритм отбора нечетких правил, где к модели добавляется текст “+ отбор”.

Метод нечеткого моделирования и анализа тенденций временных рядов применяется для моделирования и прогнозирования временного ряда статьи 211 по данным бухгалтерской отчетности “Доходы и расходы” бюджетной организации. Данные, образующий ВР, характеризуют месячные расходы на заработную плату за четыре с половиной года (рис. 1). Для этого нестационарного ВР проводился прогноз на один интервал сначала (а) для усеченного ВР на 3 точки, (б) затем – на две точки, (в) затем на одну точку, в заключении (с) исследован весь временной ряд. Целью такого исследования одного и того же временного ряда – проанализировать устойчивость краткосрочного прогноза авторских нечетких моделей по сравнению с известными S- и D-моделями. Результаты лучших моделей приведены в табл. 2.

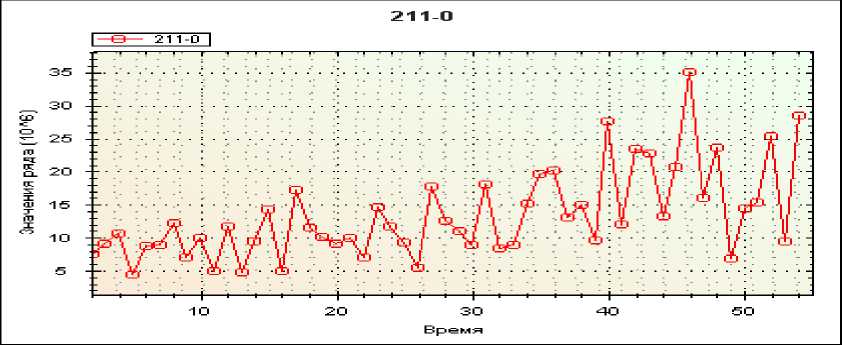
Рис. 1. Временной ряд статьи 211

Таблица 2. Показатели внешних мер качества. Прогноз на один интервал

	Название модели	МАРЕ	TTend	MSE
(а)	F2S(10,1,1)	5,4	0	0,69*10^12
	S(10,1,1)	0,6	50	0,8*10^10
	D(10,3,1)	9,4	0	0,2*10^13
(б)	F2S(10,1,1)	8,2	0	0,43*10^13
	S(10,3,1)	22	0	0,3*10^14
	D(10,1,1)	42	50	0,1*10^15
(в)	F1N(10,1,1)	5,9	0	0,1*10^13
	S(10,4,1)	17	0	0,28*10^13
	D(10,1,1)	52	0	0,24*10^15
(с)	F1N(10,2,1)	4	0	0,1*10^13
	S(10,4,1)	30	0	0,78*10^14
	D(10,1,1)	29	0	0,7*10^14

Таблица 3. Показатели внешних мер качества. Прогноз на три интервала

Название модели	MAPE	RMSE	TTend
F1N(3,3,3)+отбор	28	70*10^5	16,6
F3N1S(3,3,3) + отбор	36	122*10^5	16,6
F2S(3,4,3) + отбор	42	80*10^5	16,6
SARIMA(1,1,1)x(1,0,0)	49	88*10^5	50
F3N1S(3,4,3) + отбор	49	101*10^5	0
F2S(3,1,3) + отбор	55	88*10^5	0

Анализ внешних мер качества показывает, что авторские модели при прогнозе на один интервал характеризируются стабильными показателями качества (МАРЕ < 10%, TTend=0), что нельзя сказать о нечетких S- и D- моделях.

Проведенное статистическое моделирование и прогнозирование данного ВР на три интервала в пакете “Статистика” показало, что наименьшее MSE соответствует модели SARIMA(1,1,1)x(1,0,0), для которой MAPE=49%, RMSE=88*10^5. При нечетком моделировании предлагаемым методом были получены следующие результаты, приведенные в табл. 3.

Таким образом, исследование предлагаемого метода нечеткого моделирования и анализа тенденций временных рядов позволяет сделать вывод о его полезности при решении задач извлечения знаний о правилах следования нечетких тенденций и краткосрочного прогноза временных рядов.