Интеграция сенсорных данных и математическое моделирование поведения подводного робота с использованием цифрового двойника

Оригинальное эмпирическое исследование

Original Empirical Research

Integration of Sensor Data and Mathematical Modeling of Underwater Robot Behavior Using a Digital Twin

Mikhail D. Gladyshev ® H , Alexey V. Rybakov ©

Astrakhan Tatishchev State University, Astrakhan, Russian Federation

Introduction. Control of underwater robotic complexes (URC) is complicated by factors, such as inertia, stochastic disturbances, and lack of navigation infrastructure. Existing approaches to modeling and predicting URS behavior are known for their weak or absent integration of data from real sensors in real time. By eliminating this gap in integrated solutions, it is possible to combine physical models, digital twins, and visualization. A promising tool for overcoming the above limitations is a digital twin (DT), which provides an accurate digital representation of an object through the integration of data from physical sensors and mathematical models. The objective of the presented study is to develop a method for predicting the dynamics of the URC using a digital twin to improve the efficiency of autonomous control.

Materials and Methods. The basis of the study was the development of a mathematical model of the motion of an underwater robotic complex. It included differential kinematics, modeling of environmental resistance, and rotation dynamics. The following sensors were used to collect and process data: incremental encoders, a three-axis accelerometer, and a gyroscope. A proportional-integral differentiating (PID) controller was applied to control the motion along each axis. The Unity Game Environment was used to visualize and test the model. It created a digital twin module with the ability to display the system state in real time. The Arduino IDE platform was used as software for low-level programming, as well as MATLAB and Python for data analysis and graphing.

Results. To verify the model, experiments were conducted on a physical model. They were compared to the simulation of the object's behavior in a virtual environment. Graphs of discrepancies between physical and simulated trajectories were presented. Statistical metrics characterizing the accuracy of the digital twin were calculated. The maximum deviation in coordinates did not exceed 5.3 mm, the average angular deviation was 3.5°. This confirmed the reliability and practical applicability of the proposed model in autonomous control of a robotic complex. It was also found that the average error along X — 3.11 mm, along Y — 2.92 mm. The average error in angle Z — 1.8°. The response time was less than 10 ms. The stability of the digital twin to minor fluctuations in the data was provided by smoothing the input data, the stability of the system regulator, and adaptation of the model to the calibration values at the start of each cycle.

Информатика, вычислительная техника и управление

Discussion and Conclusion. Digital twins are suitable for predictive control and monitoring of an object under uncertainty. The proposed approach can be scaled for various types of robotic systems operating in aggressive and poorly predictable environments. Further research in this area may involve the introduction of adaptive and neural network control methods.

Введение. В последние годы растет интерес к технологии цифровых двойников (digital twin — DT ). Это виртуальные модели, тесно связанные с физическими объектами и предназначенные для отображения, анализа и прогнозирования их поведения в реальном времени [1]. DT широко применяются для решения прикладных задач в промышленности, энергетике и транспорте, особенно если необходимы контроль и управление объектами в условиях высокой неопределенности [2] . При распространении автономных робототехнических систем цифровой двойник становится важным инструментом, обеспечивающим надежное и устойчивое управление. Он позволяет формировать предсказательную модель поведения объекта, учитывающую как внутренние параметры, так и внешние воздействия [3].

Особый интерес представляет применение DT в управлении подводными робототехническими комплексами (ПРТК), где условия эксплуатации значительно осложнены слабой видимостью, отсутствием точной навигации, задержками связи, высокой инерционностью, шумами в сенсорных данных. Все это снижает эффективность традиционных замкнутых систем управления [4] . В открытом доступе есть публикации о цифровых двойниках, однако тема все еще недостаточно разработана с точки зрения использования DT в подводных системах. Имеющиеся исследования, как правило, либо не охватывают задачи предиктивного управления, либо не учитывают специфику подводной среды и типичные ошибки сенсоров [5] . Для многих работ характерны существенные пробелы, связанные с отсутствием интегрированных решений по построению цифровых двойников подводных робототехнических комплексов, ориентированных на устойчивое предсказательное управление и оценку состояния в условиях шумных и неполных данных.

Требуется устойчивая оценка текущего состояния подводного робототехнического комплекса (ПРТК), и ее может обеспечить интеграция сенсорных данных — акселерометрии, гироскопии, энкодерных измерений и других источников. Однако из-за нестабильности и шумов, типичных для инерциальных сенсоров, необходимо реализовать алгоритмы фильтрации, коррекции и калибровки данных на разных этапах работы [5] .

Отметим также, что в литературе, посвященной цифровому моделированию и управлению робототехническими системами, авторы часто делают акцент на статических моделях или на ограниченных сценариях управления (например, на навигации или стабилизации положения). В то же время недостаточно проработан комплексный подход к прогнозированию именно динамического поведения ПРТК с применением цифровых двойников в реальном времени.

В связи с вышесказанным, цель настоящего исследования — разработка и применение метода прогнозирования динамического поведения ПРТК с использованием цифрового двойника для повышения эффективности управления автономной системой при выполнении подводных инженерных работ.

Материалы и методы. Для достижения цели исследования реализована комплексная модель, включающая физико-математическое описание движения, сенсорную архитектуру и визуализацию.

Научные изыскания позволили решить следующие задачи:

• -    построение обобщенной математической модели движения ПРТК с учетом внешней среды и сенсорной архитектуры;

• -    формализация поведения автономной системы с учетом инерционных и управляющих воздействий;

• -    реализация системы управления с обратной связью на основе классических подходов теории автоматического управления;

• -    оценка точности цифрового двойника путем анализа расхождений между физическим и виртуальным поведением ПРТК на основе экспериментов;

• -    визуализация цифрового двойника в программной среде Unity с возможностью сравнения показателей виртуальной и физической траекторий.

В рамках представленной работы:

• -    создали математическую модель движения ПРТК;

• -    собрали и откалибровали данные с сенсоров;

• -    реализовали цифровой двойник в среде Unity;

• -    экспериментально верифицировали модель;

• -    проанализировали результаты и оценили точность модели.

Движение ПРТК описывается на основе дифференциальной кинематики и уравнений, учитывающих сопротивление воды, инерционные характеристики системы и управляющие воздействия. В основе модели — система уравнений движения второго порядка, модифицированная с учетом гидродинамического сопротивления и корректирующих коэффициентов, полученных экспериментально. Приняты допущения о жесткости корпуса, незначительном дрейфе и квазистационарном движении.

Вектор состояния системы включает координаты: x , y , z , и курсовой угол θ, а также линейные и угловые скорости. Используемые во введении формулы описывают кинематические соотношения, обратную связь, модель сопротивлений и управляющие сигналы. Для управления по продольной, поперечной и вертикальной осям используются ПИД-регуляторы с параметрами, эмпирически подобранными по результатам отклика системы.

Для сбора данных в режиме реального времени использовали модульную сенсорную систему. Ее элементы:

• -    энкодеры 38S6G5-B-G24N, 2000 импульсов на оборот — для оценки линейного перемещения;

• -    трехосевой акселерометр LIS3DH (диапазон измерений ±2g/±4g/±8g/±16g, интерфейсы I2C/SPI, частота дискретизации до 5,3 кГц) — для получения данных об ускорениях и наклоне;

• -    гироскоп в составе IMU-модуля (англ. inertial measurement unit, инерциальный измерительный блок) — для отслеживания угловых скоростей и ориентации.

Сенсорные данные предварительно фильтровали, калибровали (нормировка относительно нулевого положения) и интегрировали в модель цифрового двойника.

Ключевой этап в построении цифрового двойника — математическое моделирование движения подводного робототехнического комплекса. Оно позволяет прогнозировать поведение объекта в различных средах [6] . В рамках данного исследования рассматривается подвижный ПРТК с жесткой физической структурой, перемещающийся в плоской (2D) или пространственной (3D) системе координат в зависимости от сценария задачи [7] . Для управления движением используется независимый привод каждого из траков, что позволяет реализовать дифференциальное маневрирование [8] .

Для моделирования положения и ориентации ПРТК на плоскости используется кинематическая модель дифференциального робота, основанная на положении центра масс (или центра геометрии) робота [9] . Пусть x и y — координаты центра масс в глобальной системе координат, θ — ориентационный угол робота (угол между продольной осью и осью OX в глобальной системе).

X = v • cos ( 0 ) , (1)

y = v • sin ( 0 ) ,                                                            (2)

a

0 = w, где v — линейная скорость центра масс (определяется по показаниям энкодеров); w — угловая скорость (получается с гироскопа или рассчитывается по разнице скоростей гусениц).

Линейная и угловая скорости связаны с индивидуальными скоростями правой v R и левой v L гусениц:

vR + vL v =    2   ^,

vR + vL w = L ’ где L — база робота (расстояние между гусеницами).

На поведение робота существенно влияет подводная среда: сопротивление воды, подъемная сила, вязкие силы, силы трения. Эти воздействия учтены в виде обобщенного возмущения F d ( t ) [10] . Система дифференциальных уравнений приобретает вид:

m • r = F u ( t ) + F d ( t ) ,                                                    ⁽⁶⁾

где M — масса робота; r ̈ — радиус-вектор положения; F u ( t ) — управляющее воздействие от системы приводов (определяется ПИД-регулятором или иным алгоритмом); F d ( t ) — возмущения среды (определяются экспериментально или задаются эмпирически).

В рамках макета и цифровой модели сопротивление среды можно учесть в виде затухающего члена:

Fd (t ) = - ku • Г (t),(7)

где k u — коэффициент вязкого сопротивления среды (настраиваемый параметр цифрового двойника).

Физический макет оснащен энкодерами, поэтому положения и ориентация ПРТК в пространстве рассчитываются через численную интеграцию скоростей, полученных с левого и правого трака:

дs = AsL +AsR ,

Информатика, вычислительная техника и управление

Д0 = AsR - AsL(9)

L, где ΔsL, ΔsR — приращения расстояния по показаниям энкодеров; Δs — приращение центра масс; Δθ — изменение ориентации.

Используем текущую ориентацию Δθ, чтобы выразить новое положение в глобальной системе координат: Xt+i = Xt + As • cos (01),(10)

y t + 1 = y t ^{+ A s} • ^sin (⁰ 1 ) ^{. (11)}

Математическое моделирование — фундаментальная часть разработки цифрового двойника подводного комплекса [11] . Целью моделирования является формализация процессов движения [12] , управления и реакции на внешние воздействия с возможностью дальнейшего анализа устойчивости и точности исполнения управляющих воздействий [13] .

Подводный робот рассматривается как система с несколькими входами и выходами, находящаяся в среде с высоким уровнем инерционности, запаздывания и стохастических возмущений [14] . Управляющие воздействия реализуются через модули тяги, а перемещения отслеживаются с помощью энкодеров и инерциальных измерительных модулей [15] . Модель можно описать как систему уравнений второго порядка с обратной связью по положению и скорости:

Mx( t) + DX (t) + Kx (t ) = Bu (t), (12) где M — матрица масс (включает инерционные характеристики); D — матрица демпфирования (учет вязкого сопротивления воды); K — матрица жесткости (включает упругие силы в случае механических ограничений); x(t) — вектор положения и ориентации в 3D-пространстве; u(t) — управляющее воздействие (сигналы на моторы); B — матрица распределения управления.

Для вращательного движения используется модель Эйлера:

Jx ( t ) + м ( t ) + J w ( t ) = т ( t ) ,                                              (13)

где J — тензор инерции робота, ω( t ) — угловая скорость (с гироскопа), τ( t ) — управляющий момент.

При реализации поворота на месте, как правило, используются траки с разным направлением вращения. Разность скоростей на правом и левом траке задает момент:

т z = rF ( W l - W r ) .                                                (14)

Для задания угла поворота используется выражение:

Z

( t ) =     W z ( t ) dt .

Система управления реализуется в виде ПИД-регуляторов по каждой оси ( X , Y , Z ):

f t . . de ( t ) e ( t ) dt + K_D ——, 0                 dt

где e( t ) = x re F ( t ) - x ( t ) — ошибка между целевым и текущим положением. Коэффициенты K p , K i , K D настраиваются по критерию оптимальности.

Коэффициенты регуляторов для стабилизации положения

Таблица 1

Ось	Kp	Ki	Kd
X	1,2	0,05	0,6
Y	1,0	0,04	0,5
Z	2,0	0,1	0,9

Физическую модель робота реализовали на базе Arduino Mega 2560 Pro. Микроконтроллер — ATMega 2560-16AU, 16 МГц, 256 КБ FLash, с 54 цифровыми вводами/выводами (I/O), 16 аналоговыми входами, USB-UART интерфейсом CH340G. Комплекс подключен к сенсорам и системе управления приводами. Данные собирали и передавали в цифровую среду через последовательный порт (Serial), в формате объединенных строк с временной меткой.

Виртуальная реализация цифрового двойника создана в Unity. C#- скрипты использовались для интерпретации данных, отображения перемещений, поворотов и поведения объекта в трехмерной среде. Визуализируются оси, контуры, значения координат и траектории. Применена модель полупрозрачного робота, не взаимодействующего с другими объектами, что позволяет сконцентрироваться на сравнении движений.

На стороне Unity были реализованы обработчик данных и система фильтрации. Для расчета углов и координат применили интеграцию с коррекцией по сенсорным данным. Отдельные блоки реализовали в виде скриптов с возможностью масштабирования проекта. Для статистической оценки точности использовали стандартные метрики: среднеквадратичное отклонение, максимальное отклонение, средняя ошибка по координатам и углам.

Результаты исследования. Для верификации модели в цифровой среде симулировались движения под действием последовательных управляющих воздействий. Затем сопоставили траектории прямолинейного и полу-кругового движения (рис. 1 и 3). Показания цифрового робота сравнивались с идеальной траекторией. Среднеквадратичный анализ показал расхождение при движении по прямой (рис. 2) и по полукругу (рис. 4).

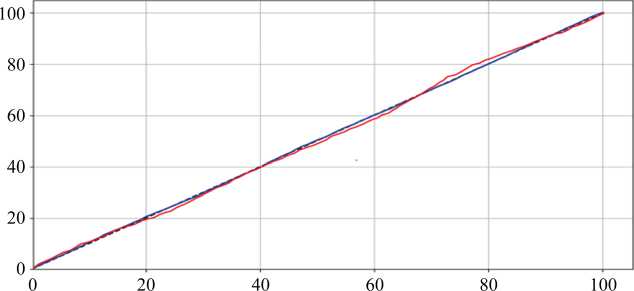
Идеальная траектория АТ    — Траектория цифрового робота — Траектория физического робота

Рис. 1. Траектории движения по прямой

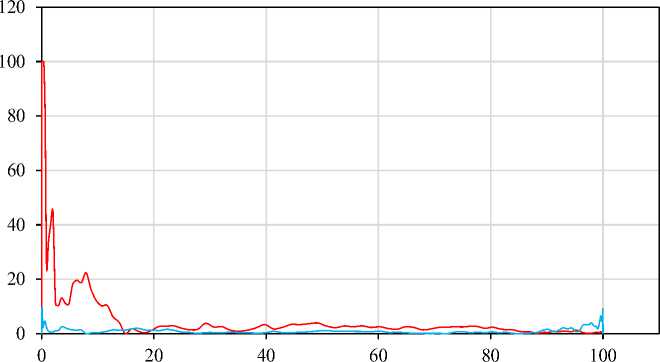
Погрешность для X       Погрешность для Y

Рис. 2. Погрешность (%) при замере на прямой

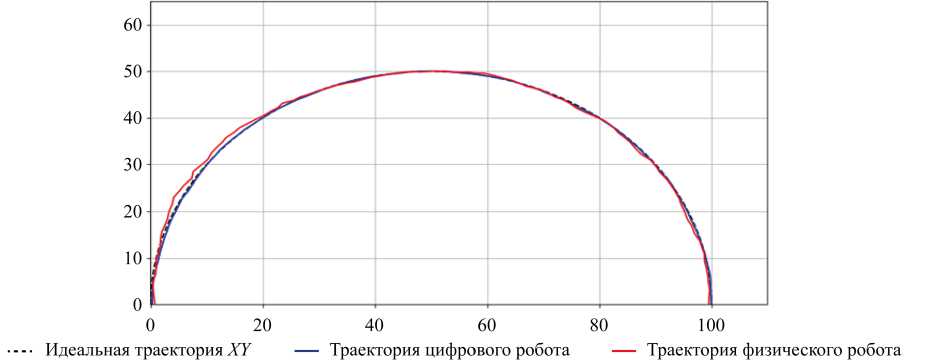
Рис. 3. Траектории движения по полукругу

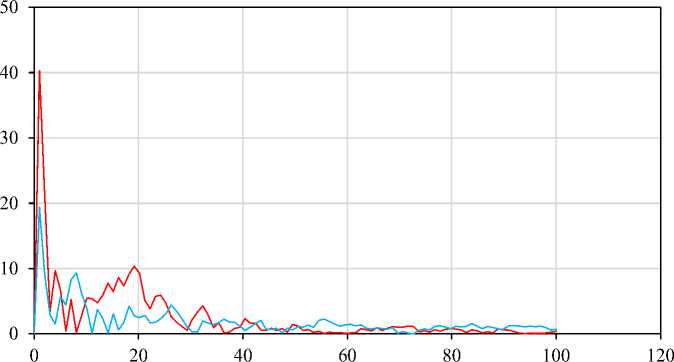
Разница по X        Разница по Y

Рис. 4. Погрешность (%) при замере на полукруге

Качество отображения поведения ПРТК в цифровом двойнике оценивали в ходе экспериментов, включающих прямолинейное движение, разворот на месте, траекторию с поворотами. Параллельно записывались данные с реальных сенсоров и сравнивались с параметрами модели в Unity. Результаты замеров и сравнений представлены в таблице 2.

Информатика, вычислительная техника и управление

Таблица 2

Метрика	Значение
Максимальное отклонение X	5,3 мм
Максимальное отклонение Y	4,8 мм
Среднее угловое отклонение	3,5°

Показатели отклонений

Цифровой двойник визуализировали в среде Unity. Этот гибкий 3D-движок позволяет встраивать потоки данных с физических сенсоров, отображать пространственные перемещения, ориентацию, а также создавать сценарии взаимодействия с внешней средой (рис. 5).

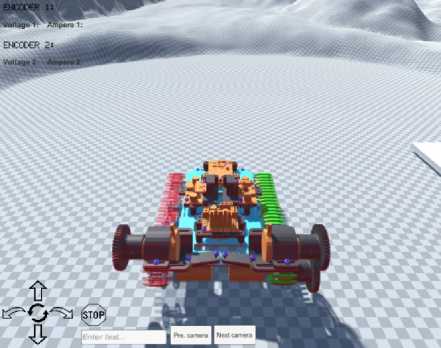
Рис. 5. Программа управления робототехническим комплексом

Данные с физических сенсоров (акселерометров, гироскопов, энкодеров) передавались через COM-порт (англ. communications port) с применением пользовательского скрипта на C#. Входящие данные разделялись по каналам и отображались как параметры объекта-двойника.

Цифровая модель в Unity использует ту же координатную систему и ту же структуру управления, что и реализованная математическая модель. Ее функции:

• -    передача команд от модели ПИД-регуляторов к виртуальным колесам;

• -    отображение положения, угла наклона, скорости;

• -    визуальное воспроизведение движения на основе интегрированных сенсорных данных.

Решение позволяет создать замкнутый цикл «модель — реальность — визуализация» и обеспечивает согласованность между цифровым двойником и физической системой (рис. 6).

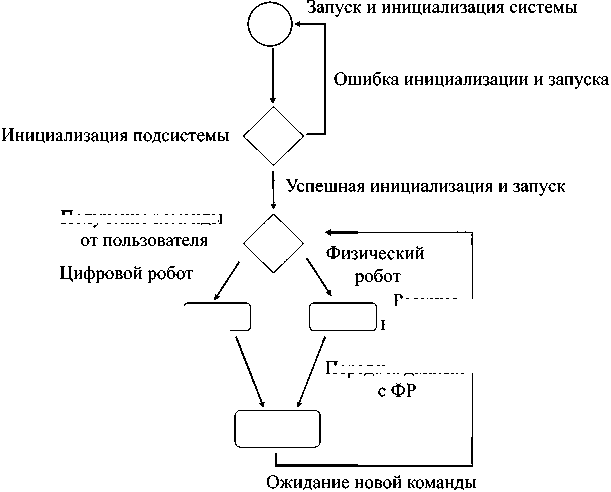
Получение команды

Реакция на команду

ФР Передача данных

Реакция на команду ЦР

Отображение данных

Передача данных сЦР

Рис. 6. Алгоритм работы программного обеспечения: ЦР — цифровой робот; ФР — физический робот

Ниже перечислены элементы алгоритма работы программного обеспечения.

Запуск и инициализация системы. Физический робот включается и через USB подключается к компьютеру, который собирает и анализирует данные, запускает главную программу и выполняет инициализацию дополнительных скриптов:

• -    отвечающих за поддержание связи и сбор данных,

• -    обеспечивающих визуализацию.

Все это происходит в Unity, после чего система готова к работе.

Инициализация робота. После запуска программы устанавливается ее связь с физическим роботом. Следовательно, происходит калибровка, а затем запускаются датчики и модули: гироскоп, акселерометр, энкодеры, вольтметр, амперметр. В Unity отправляется контрольное сообщение о готовности робота к запуску и старте передачи данных. После этого наступает этап ожидания команд.

Получение команды от пользователя. Анализируется и обрабатывается значение вводимого в программу пользовательского интерфейса. Передается сообщение промежуточным скриптам для выполнения действий цифрового и физического робота.

Реакция на команду цифрового робота. Введенные значения и действия записываются в память компьютера. На основе заложенных алгоритмов выполнения команд и математической модели цифровой робот движется в цифровом пространстве. При этом фиксируются данные о его положении, скорости и пройденном расстоянии. После выполнения команды робот сохраняет положение и ориентацию в пространстве.

Реакция на команду физического робота. Данные передаются на микроконтроллер Arduino Mega. Здесь они анализируются и в зависимости от введенной команды и значения задействуют скрипты, отвечающие за работу датчиков: левого и правого энкодера, акселерометра и гироскопов. Только после этого начинается движение по команде пользователя. В процессе выполнения команды робот фиксирует свое положение и ориентацию в пространстве и передает данные в программу пользовательского интерфейса, где данные визуализируются при помощи 3D-модели, привязанной к физическому роботу.

Сбор и отображение данных. На этом этапе данные о положении, углах наклонов, пройденном расстоянии и других параметрах собираются с цифрового и физического робота и визуализируются в программе пользовательского интерфейса. После этого программа ждет новую команду.

Описанный алгоритм основан на классических принципах замкнутых систем управления с обратной связью. Использование данных с сенсоров (акселерометров, гироскопов, энкодеров) позволило реализовать элемент измерителя в общем структурном виде систем управления. Математическая модель, интегрированная в Unity, выступила в роли наблюдателя, отслеживающего поведение системы и позволяющего визуально верифицировать корректность выполнения команд.

Система проектировалась с учетом:

• -    линеаризации модели движения ПРТК в малых окрестностях траектории,

• -    ПИД-регулирования угла поворота и скорости,

• -    фильтрации сенсорных данных с применением простых скользящих окон и корректировок по нулевой калибровке.

В формулах (17)–(19) представлены показатели, которые использовались для анализа точности цифрового двойника. Абсолютная ошибка положения (в мм):

Информатика, вычислительная техника и управление

Ax ( t )| xreal ( t )-xdigit ( t )|.                                                            (17)

Среднеквадратичная ошибка ориентации (в градусах):

A⁰ П E ( ⁰ reali -⁰ d'git^ (18)

Процентное отклонение финального положения:

^^fa . 100%.                                  (19)

x real

В результате экспериментов и анализа показаний датчиков получены дополнительные параметры, характеризующие погрешность разрабатываемой системы (таблица 3).

Выявленные погрешности системы

Таблица 3

Параметр	Значение
Средняя ошибка по Х	3,11 мм
Средняя ошибка по Y	2,92 мм
Средняя ошибка угла Z	1,8о
Максимальное отклонение	5,3 мм
Время реакции	<100 мс

Цифровой двойник устойчив к незначительным флуктуациям в данных благодаря следующим факторам:

• -    сглаживание входных данных;

• -    устойчивость регулятора, реализованного в системе;

• -    адаптация модели к калибровочным значениям при старте каждого цикла.

Обсуждение и заключение. Разработана и экспериментально подтверждена модель цифрового двойника робототехнического комплекса, основанная на интеграции сенсорных данных, математического моделирования и 3D-визуализации. Реализовано устойчивое управление и отслеживание поведения ПРТК. Представлены результаты сравнительного анализа цифровой модели и реальной системы. Итоги сопоставления доказали:

• -    высокую степень соответствия поведения цифрового двойника реальному объекту;

• -    эффективность выбранных алгоритмов калибровки и обработки данных;

• -    перспективность использования цифровых двойников при отладке автономных систем, если физическое тестирование затруднено.

Построенная модель позволяет адекватно оценивать текущее состояние и прогнозировать поведение ПРТК в условиях неопределенности. ПИД-регуляторы обеспечивают устойчивость при управлении, а визуализация в Unit y дает возможность реализовать цифровой двойник как интерфейс взаимодействия с системой. Дальнейшее развитие этого решения может быть связано с внедрением адаптивных и нейросетевых методов управления.