Интеграция сверточной нейронной сети в систему распознавания образов

Данная статья посвящена описанию программного модуля детектирования объектов на основе технологии стереозрения, разработанного в рамках магистерской диссертации [12]. Данный модуль выделяет объекты и осуществляет слежение за ними. Однако при изменении условий окружающей среды (изменение освещения) качество распознавания резко падает. Изобилие систем машинного зрения не устраняет главные недостатки систем распознавания (погрешность распознавания при изменении ракурса объекта, изменение освещения, чувствительность ПО и т.д.). На сегодняшний день лучшие результаты в распознавании образов получают с помощью сверточных нейронных сетей (СНС). При достаточно большом размере СНС имеют небольшое количество настраиваемых параметров, довольно быстро обучаются. Именно поэтому для дальнейшей разработки системы распознавания были выбраны СНС.

Архитектура сверточных нейронных сетей

На рисунке 1 представлена структура сверточной нейронной сети (СНС). СНС состоит из двух основных частей [9]:

- часть, отвечающая за выделение признаков;

- часть, с помощью которой производится классификация.

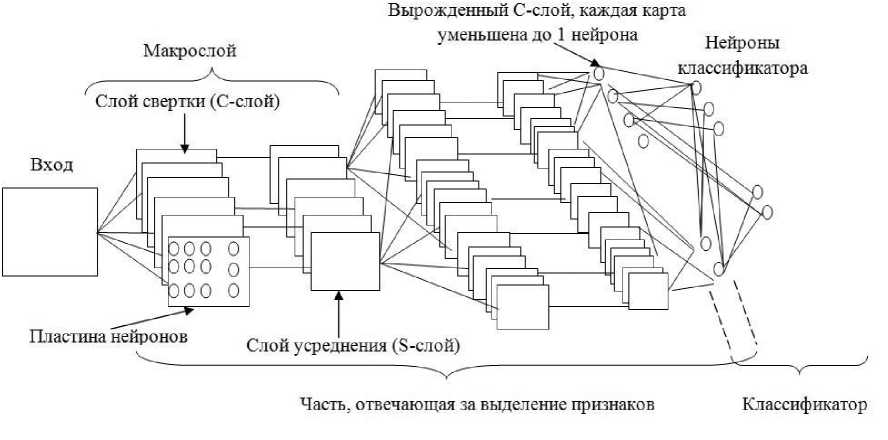
Рис. 1. Общая структура сверточной нейронной сети

Выделитель признаков состоит из нескольких слоёв. Каждый слой составляют пластины нейронов. Слои СНС имеют разные функции. Нейроны группируются в пластины для того, чтобы обрабатывать входные сигналы с сохранением топологических отношений, которые потерялись бы, если входной сигнал подается в виде вектора, а не матрицы. Классическая архитектура СНС включает в себя два типа слоёв: слои свертки (C-слои) и слои усреднения ( S -слои). Слои с разными функциями можно объединяются в один макрослой. Выделитель признаков состоит из повторяющихся несколько раз идентичных макрослоёв. Каждый нейрон в выделителе признаков имеет своё рецептивное поле (РП), представляющее из себя квадратную область, которая включает в себя нейроны, способные передавать свои сигналы нейрону на следующем слое. Для СНС с классической архитектурой макрослой - это C-слой, за которым следует S -слой [5]. На рисунке 2 показан общий вид C-слоя, представлен процесс его взаимодействия с предыдущим слоем [9].

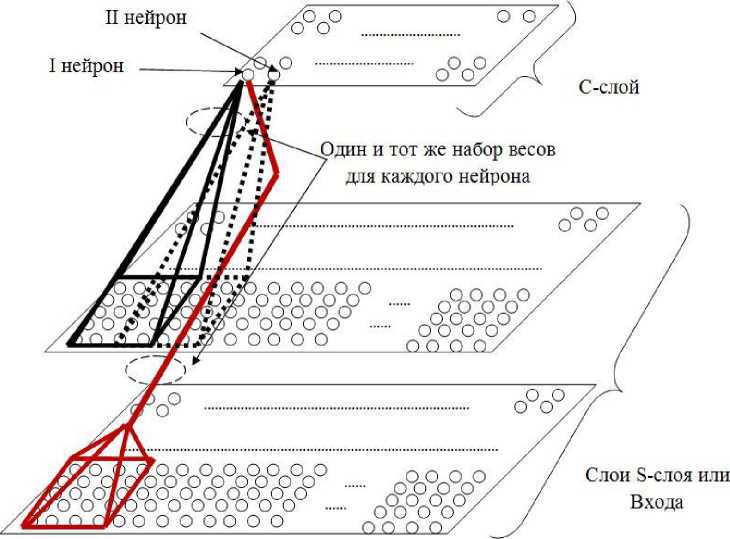
Рис. 2. Схема взаимодействия С-слоя с предыдущим слоем

Каждая карта С-слоя может быть связана с некоторым количеством карт предыдущего слоя. На рисунке 2 видно, что карта С-слоя связана с двумя картами S -слоя или входного слоя, которые располагаются перед ней. Тогда каждый нейрон С-слоя имеет рецептивное поле (РП) сразу на двух картах в идентичных позициях предыдущего слоя. На рисунке эти поля обозначены сплошным черным и красным цветом и имеют размер 4*4. Следовательно, для нейрона С-слоя с учетом смещения необходимо 33 настраиваемых параметров (весов). Ключевая особенность С-слоя - для всех нейронов используются одни и те же веса, т.е. на данную карту С-слоя будет приходиться 33 параметра, а не 33 умноженное на количество нейронов в слое. Такие веса называются связанными ( sharing weights ). Связанные веса позволяют выделять некоторый признак в любом месте карты. Связь карты С-слоя с несколькими картами предыдущего слоя позволяет единым образом реагировать на информацию из разных модальностей (по-разному отфильтрованную) [14]. Черным пунктиром на рисунке 2 обозначено РП для следующего нейрона. Эти РП пересекаются, при этом шаг пересечения регулируется. Чем меньше шаг, тем больше РП можно наложить на карту, при этом возрастает количество нейронов в карте следующего слоя. Рецептивные поля и общие веса - это встроенная априорная информация, за счёт которой происходит выделение признаков [13]. На рисунке 3 показана схема нейрона С-слоя [9].

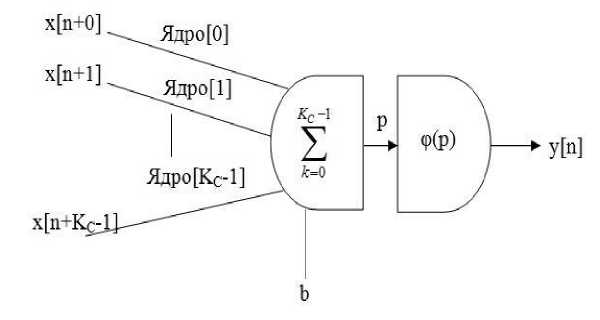
Рис. 3. Общая схема нейрона С-слоя

K c - общее количество нейронов, входящих в РП n -го нейрона С-слоя, Ядро[ к ] - настраиваемые веса нейрона, b - смещение n -го нейрона, причём b и Ядро[ к ] - одни и те же для всей карты С-слоя, x[n+k] - входные данные для n -го нейрона С-слоя, к = 0..K c -1. Входные данные x[n+k] дают взвешенную сумму с настраиваемыми параметрами Ядро[ к ], т.е. происходит операция свертки (4.1):

» = £>+ V Ядро. *х _z

(4.1)

Реакция нейрона определяется функцией активации, на вход которой подаётся взвешенная сумма p . При этом выход нейрона имеет вид (4.2):

| У = ^(р)

(4.2)

Каждый нейрон С-слоя - это детектор некоторого признака, выделенного в процессе обучения признака. На рисунке 4 показаны примеры признаков, на которые могут реагировать нейроны С-слоя. На данном слое проводится свёртка отдельной области входного сигнала со своими настраиваемыми параметрами, одинаковыми для всех нейронов. После этого свертка пропускается через функцию активации, полученный результат свидетельствует о степени присутствия данного признака в позиции РП этого нейрона. Свертка элемента входа с общими настраиваемыми параметрами есть аналог пропускания изображения на карте через некоторый фильтр [7]. Изображение, формируемое на карте С-слоя, является отфильтрованным изображением относительно настраиваемых весов.

Рис. 4. Примеры признаков, на которые реагируют обученные нейроны С-слоя

На рисунке 5 представлена схема взаимодействия S-слоя с предыдущим C-слоем [9]. Основная задача S-слоя - уменьшение масштаба обрабатываемого отфильтрованного отображения, которое получается на карте предыдущего С-слоя. Это необходимо для облегчения выделения общих признаков. Каждая карат S-слоя связана только с одной картой предыдущего С-слоя.

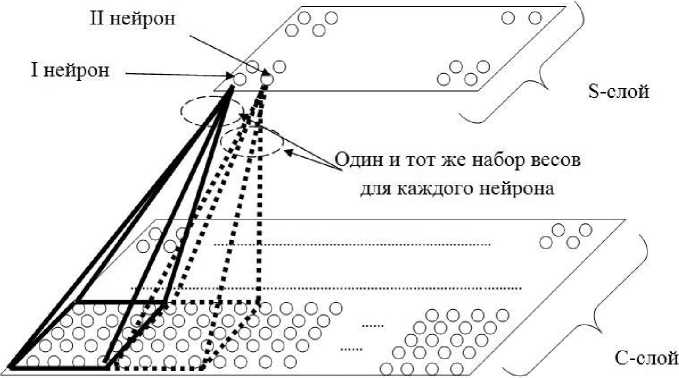
Рис. 5. Общая схема взаимодействия S-слоя с предыдущим C-слоем

Рецептивные поля нейронов S -слоя не пересекаются. Настраиваемые параметры являются общими для всех нейронов каждой карты, но их количество равно двум и не зависит от количества элементов, входящих в РП этих нейронов. Общая схема нейрона S -слоя представлена на рисунке 6 [9].

x[n*Ks+O]

x[n*Ks-l]

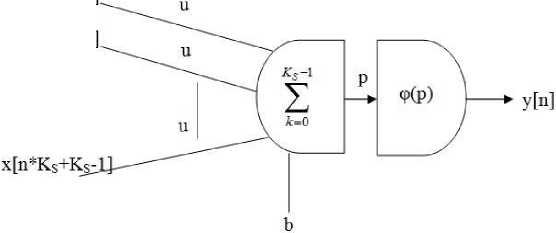
Рис. 6. Общая схема нейрона S-слоя

Из рисунка 6 видно, что все настраиваемые параметры нейрона, которые участвуют в свертке с элементом входа, равны (параметр u ). Другой настраиваемый параметр – это смещение b . Параметры u и b – одинаковы для всех нейронов S -карты. С учетом того, что РП не пересекаются, свертка p для n -го нейрона S -слоя определяется как (4.3):

^-1

P = b+u* ^x,.^

(4.3)

В формуле (4.3) K S – общее количество нейронов, входящих в РП n -го нейрона S -слоя. На рисунка 1 видно, что общий размер карт уменьшается от слоя к слою до тех пор, пока карты не вырождаются в единичные нейроны. При этом уменьшение размера карт (и связанного с этим потерей точности отображений на них) компенсируется ростом количества карт, а также связями между картами С-слоя и слоем перед ним. Вторая часть СНС – это классификатор признаков. Это, как правило, однослойный или двухслойный персептрон. Карты, выродившиеся в один нейрон можно считать за вход для классификатора, над его входом надстраивается слой обычных нейронов, где каждый нейрон связан со всеми нейронами входа. Количество нейронов в слое классификатора обычно соответствует количеству классов, к которым требуется отнести входное изображение. Связанных весов в классификаторе нет. Общая схема нейрона для слоя классификатора показана на рисунке 7 [9].

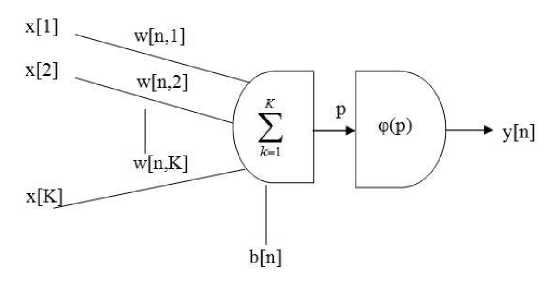
Рис. 7. Общая схема нейрона для слоя классификатора

Взвешенную сумму p для нейрона слоя классификатора можно определить как (4.4):

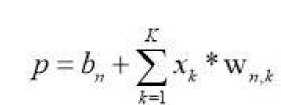
(4.4)

В формуле (4.4) b n — это смещение, разное для каждого нейрона, x[k] - элемент входа, w[n,k] -настраиваемые параметры n -го нейрона, уникальные для каждого нейрона, K - размер входа для слоя классификатора.

На основе анализа литературы [5, 10, 1-4], которая посвящена созданию и обучению СНС, для использования в системе распознавания была выбрана классическая архитектура СНС, включающая слои свертки и усреднения. Реализация классической СНС на программном уровне довольно проста. Отказ от простого уменьшения зоны пересечения рецептивного поля и введение этапа усреднения положительно сказывается на качестве распознавания. Схема обучения СНС – обучение с учителем. Основные плюсы данной схемы – относительная простота архитектуры, наличие учителя (меток), что делает процесс обучения довольно четким и понятным, а качество распознавания при этом повышается. Существенный минус данной схемы обучения – большая сложность создания обучающих выборок, однако при небольшом количестве классов негативным влиянием данного фактора можно пренебречь. На рисунке 8 представлена общая схема обучения с учителем [9].

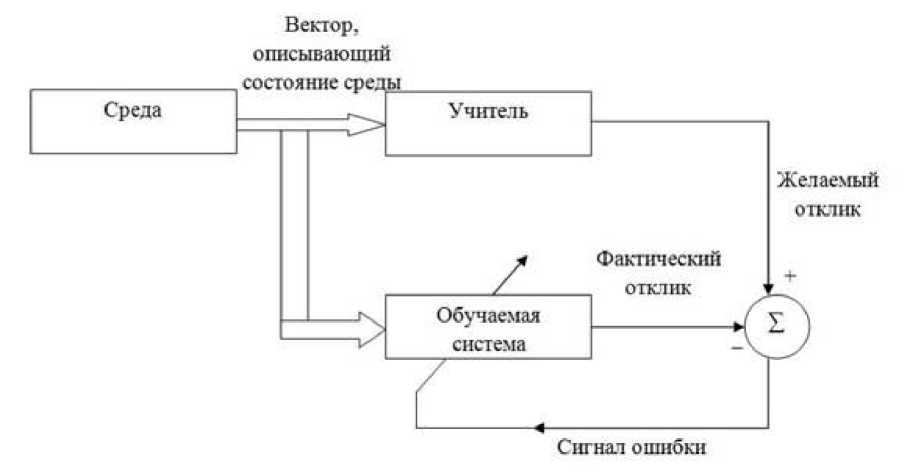
Рис. 8. Блок-схема процесса обучения с учителем

Применительно к задаче распознавания учитель – это номер некоторого класса, который закодирован в векторе. Данный вектор равен размеру выходного слоя нейронной сети. Это желаемый результат, соответствующий данному входному паттерну. Фактический отклик получается в результате реакции нейронной сети (обучаемая система) с текущими параметрами на входной паттерн. Сигнал ошибки – разность между желаемым сигналом и текущим откликом нейронной сети. Именно на основе сигнала ошибки корректируются настраиваемые параметры нейронной сети [13].

Функция ошибки зависит от настраиваемых параметров системы. Для такой функции можно построить многомерную поверхность ошибки в координатах свободных параметров. При этом реальная поверхность ошибки усредняется по всем возможным примерам, которые представлены в виде пар «вход – выход». Для повышения производительности системы во времени значение ошибки должно смещаться в сторону минимума. Этот минимум может быть как локальным, так и глобальным [13]. Наиболее распространенными и надежными методами достижения локального или глобального минимума на поверхности ошибок являются методы локальной оптимизации [6, 8, 11]. Все алгоритмы локальной оптимизации можно разделить на два класса: алгоритмы локальной оптимизации с вычислением частных производных первого порядка (метод наискорейшего спуска, метод одномерной и двумерной оптимизации целевой функции в направлении антиградиента, метод сопряжённых градиентов, методы, учитывающие направление антиградиента на нескольких шагах алгоритма и др.) и алгоритмы локальной оптимизации с вычислением частных производных первого и второго порядков (метод Ньютона, методы оптимизации с разряженными матрицами Гесса, квазиньютоновские методы, метод Гаусса-Ньютона, метод Левенберга-Марквардта и др.). В данной работе используется классический алгоритм обратного распространения ошибки.

Проектирование СНС и реализация

Основным и наиболее важным этапом реализации системы распознавания на основе СНС является этап формирования обучающей выборки. В обучающую выборку вошли 10 классов объектов (шар, человек(лицо), кубик, цилиндр, игрушечная машина, шариковая ручка, самолет, кружка, чайная ложка, фармацевтический флакон). Общий объем обучающей выборки – 50 000 изображений (по 5000 на каждый класс). Объем тестовой выборки – 10 000 изображений. Формировалась обучающая выборка частично из собственноручно заснятых изображений, частично из изображений, загруженных из Интернета. Все изображения предварительно обработаны (размер 32x32, RGB , масштабирование с сохранением размера, зеркальное отображение) и разделены в соответствии с их классификацией. Проектирование, создание и обучение СНС производились с помощью библиотеки Keras. Структура СНС задается с помощью данной библиотеки непосредственно в программном коде, что довольно удобно. Структура используемой СНС представлена на рисунке 9.

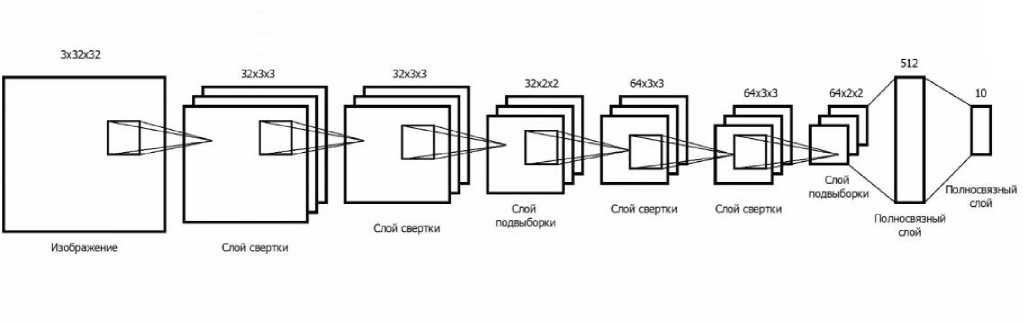
Рис. 9. Структура используемой в системе СНС

На вход СНС поступают изображения размером 32x32 в трех каналах (RGB). На первом сверточном слое используется 32 карты признаков размером 3x3, т.е. каждый нейрон сверточного слоя подключен к квадратному участку изображения размера 3x3. В данном слое используется 32 разных карты признаков, каждая с собственным ядром свертки. Следующий сверточный слой имеет такую же архитектуру. Слои свертки и слои подвыборки предназначены для выделения признаков на изображениях (границы, простые цвета и кривые). После повторного применения набора фильтров

(изображение проходит через второй свёрточный слой) на выходе будут активируются фильтры, которые представляют свойства более высокого уровня. Типами этих свойств могут быть полукольца (комбинация прямой границы с изгибом) или квадратов (сочетание нескольких прямых ребер). Чем больше свёрточных слоёв проходит изображение и чем дальше оно движется по сети, тем более сложные характеристики выводятся в картах активации. На слое подвыборки происходит уменьшение размерности (нелинейное уплотнение карты признаков). Слой подвыборки получает на вход маленькие отдельные фрагменты изображения (обычно 2х2) и объединяет каждый фрагмент в одно значение. Существует несколько возможных способов агрегации, наиболее часто из четырех пикселей выбирается максимальный. Этот способ схематически изображен на рисунке 10. Эксплуатируется тот факт, что изображения обладают свойством локальной скоррелированности пикселей — соседние пиксели, как правило, не сильно отличаются друг от друга. Таким образом, если из нескольких соседних получить какой-либо агрегат, то потери информации будут незначительными. В данной архитектуре сети считается, что информация о факте наличия искомого признака важнее точного знания его координат, поэтому из нескольких соседних нейронов карты признаков выбирается максимальный и принимается за один нейрон уплотнённой карты признаков меньшей размерности. За счёт данной операции, помимо ускорения дальнейших вычислений, сеть становится более инвариантной к масштабу входного изображения. Один проход Свертка– Подвыборка влияет на изображение следующим образом: он сокращает длину и ширину определенного канала, но увеличивает его значение (глубину) (рисунок 10). Полносвязный выходной слой из 10 нейронов содержит вероятности принадлежности объекта на анализируемом изображении к определенному классу.

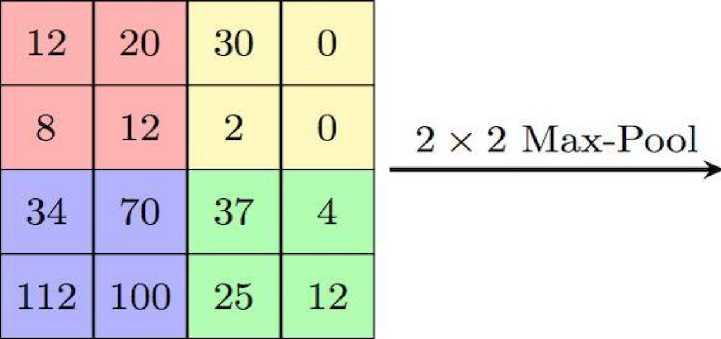
Рис. 10. Уменьшение размерности на слое подвыборки

20	30
112	37

Оценка качества распознавания проводилась после 20, 25 и 30 итераций обучающего алгоритма по всему обучающему множеству. Лучшие показатели точности распознавания отмечены после 30 итераций. На обучающей выборке процент верно распознанных объектов – 82%, а на тестовой выборке – 80% (рисунок 11).

Epoch 20/20

50000/50000 [——=—————] - 356s loss: 0.6422 - acc: 0.7786 - val_loss: 0.6876 - val_acc: 0.7648

Epoch 25/25

50000/50000 [==============================] - 354s loss: 0.6231 - acc: 0.7950 - val_loss: 0.6644 - val_acc: 0.7850

Epoch 30/30

50000/50000 [——=—————] - 358s loss: 0.5931 - acc: 0.8236 - val_loss: 0.6125 - val_acc: 0.8074

Рис. 11. Оценка точности распознавания

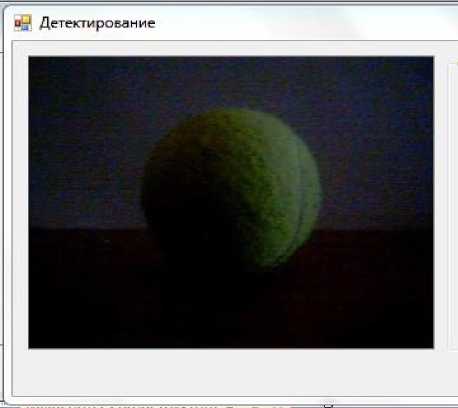
На рисунке 12 наглядно представлено повышения качества распознавания при использовании СНС в системе распознавания образов. Эксперимент проведен с объектом, изображение которого отсутствовало в обучающей выборке.

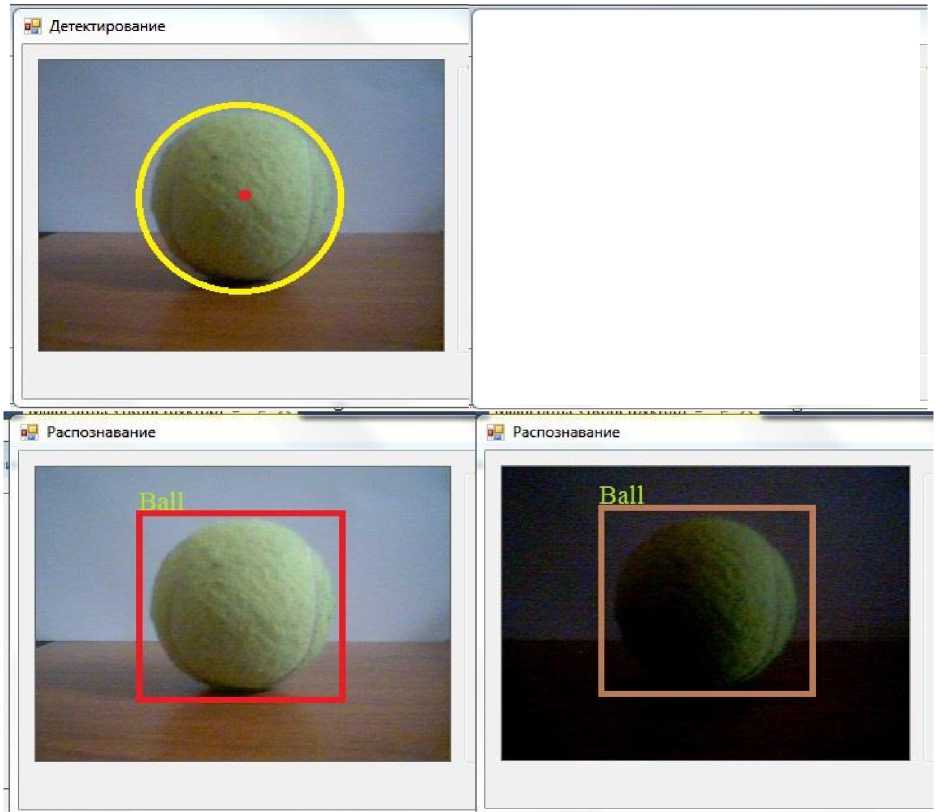
Рис. 12. Распознавание без использования СНС (вверху), распознавание с использованием СНС (внизу)

Заключение

В данной статье рассмотрена архитектура сверточных нейронных сетей, которые в настоящее время являются одним из лучших инструментов для решения задач распознавания и классификации, также в работе приведено описание разработанной системы распознавания объектов различных классов. С помощью данной системы наглядно продемонстрированы преимущества использования нейронных сетей в задаче распознавания образов, которая на данный момент далека от решения и очень актуальна. Использование нейросетевого подхода позволило значительно снизить негативное влияние внешних факторов на качество распознавания (погрешность распознавания при изменении ракурса объекта, изменение освещения, чувствительность ПО и т.д.).