Интегральная модель и численный метод определения температуры при линейном теплопереносе

Развитие современных технологий в металлургии, машиностроении, химической промышленности неразрывно связано с исследованием процессов теплопереноса. Результаты этих исследований служат основой для выбора режима внешнего теплового воздействия, под действием которого формируются требуемые теплофизические характеристики объекта, а также осуществляется температурный контроль процесса теплопереноса.

При реализации многих технологических процессов связанных, например, с вторичной или комплексной термообработкой, прокаткой труб, конструкция оборудования позволяет измерять температурные функции только вблизи поверхности объекта. В этих случаях возникает необходимость в разработке математических моделей и численных методов определения температуры в недоступной для измерений части объекта по результатам поверхностных измерений. Подобные задачи возникают при термообработке, при технической диагностике работы оборудования в паровых и газораспределительных системах.

Задачи, в которых требуемые значения физической величины находят из результатов кос- венных измерений вблизи поверхности, относят к классу обратных граничных задач. Существенная особенность обратных задач заключается в том, что при применении общепринятых численных алгоритмов [1, 2] получают приближенные решения, неустойчивые относительно погрешности исходных данных, т. е. незначительные погрешности исходных данных приводят к большим погрешностям в решении или вовсе к неверному результату. Таким образом, возникает необходимость в разработке численных методов, устойчивых относительно погрешности исходных данных. Основным подходом к построению подобных методов является использование регуляризующих алгоритмов.

Исследованию обратных граничных задач, связанных с процессами теплообмена, посвящены работы О.А. Алифанова [3], С.И. Кабанихина [4], А.И. Короткого [5], Д. Бека [6]. С разработкой и исследованием численных методов и регуляризующих алгоритмов связаны работы А.С. Апар-цина, А.Б. Бакушинского [7], В.В. Васина [8], Г.И. Марчука [9] и других исследователей [10, 11].

В работе рассмотрена задача теплопереноса, в которой внешнее тепловое воздействие на объект одинаково в каждой точке поверхности. В этом случае задача определения температуры во внутренних точках имеет вид задачи теплопереноса в линейном объекте, один конец которого соответствует точке на поверхности тела, а второй – внутренней контрольной точке. Специфика технологического процесса, связанного с термообработкой, исключает существенные изменения основных теплофизических характеристик материала, поэтому полагаем, что теплопроводность, удельная теплоемкость и плотность являются постоянными величинами. Исходные данные в задаче формируются в соответствии с результатами измерения температуры, полученными от температурных датчиков, расположенных вблизи поверхности объекта.

Математическая модель процесса распределения тепла внутри линейного объекта включает уравнение теплопроводности, значения температуры во внутренних точках линейного объекта в начальный момент времени, граничные условия, которые формируются из результатов измерения температурных функций на одной из границ объекта и вблизи нее.

В рассматриваемой задаче измерения уравнение теплопроводности с помощью прямого и обратного преобразования Лапласа приводится к интегральному уравнению Вольтерра, представляющему прямую зависимость неизвестной температурной функции от исходных данных. Преобразование Лапласа для приближенного решения уравнения теплопроводности применялось многими исследователями [10, 12, 13].

В данной работе, в отличие от известных методов, предложен подход, состоящий из двух этапов. На первом этапе формируется интегральная модель задачи теплопереноса, характеризующая линейную зависимость неизвестной температурной функции от исходных данных, а затем для численного решения полученного уравнения используется метод регуляризации, обеспечивающий устойчивость вычислительной процедуры относительно погрешности исходных данных. Преимущество предложенного подхода заключается в том, что полученное на первом этапе интегральное уравнение Вольтерра I рода напрямую связывает искомую температурную функцию и исходные данные. Теоретические аспекты интегральных уравнений, а также методы их решения являются хорошо исследованной областью. Представленный в работе численный метод решения интегрального уравнения основан на принципах естественной регуляризации и является обобщением результатов, изложенных в работе [11].

С целью оценки эффективности предложенного подхода проведен вычислительный эксперимент, который включает сравнительный анализ найденных значений неизвестной температурной функции и тестовых значений, а также определение температурной функции во внутренних точках линейного объекта на основе вычисленных граничных функций. В работе приведены результаты вычислительного эксперимента, которые свидетельствуют о достаточной точности предложенного вычислительного метода.

Постановка задачи

Рассмотрим задачу измерения, связанную с процессом теплопереноса в однородном теле, у которого теплофизические характеристики материала: удельная теплоемкость, теплопроводность и плотность несущественно изменяются в пространстве и времени. Полагаем, что объект не содержит внутренних источников энергии. Процесс претерпевает плавные изменения, без фазовых переходов.

Измерения температуры проводятся в граничной области. Схема измерения представлена на рис. 1. Датчики измеряют температуру в точках А 1 и %₀ . В задаче измерения требуется опреде-

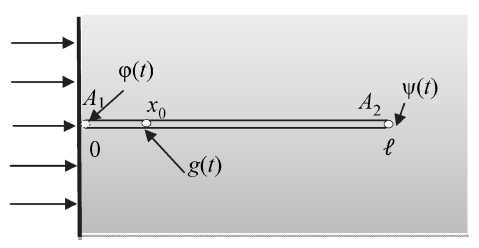
лить изменение температуры внутри тела, вплоть до контрольной точки А 2 . Реализация данной схемы измерения рассмотрена, например, в работе [3].

Рис. 1. Схема измерения температуры: А 1 , х ₀ - точки, в которых проводятся измерения температуры, А 2 – контрольная точка, в которой требуется определить температуру

Введем следующие обозначения: t – время, x – расстояние от поверхности до контрольной точки линейного объекта, Я - длина линейного объекта А 1 А 2 , функция u ( x , t ) характеризует значение температуры в точке ( x , t ) . Функция p ( t ) = и ( 0, t ) формируется по результатам измерения температуры на поверхности тела в точке А 1 , а функция g ( t ) = и ( x₀, t ) - по результатам измерения в точке x ₀ . В начальный момент времени температура объекта была постоянной С . В задаче требуется определить температуру и ( Я , t ) = ф ( t ) в контрольной точке А 2 .

Учитывая, что в технологическом процессе недопустимы резкие перепады температур и температурных градиентов, полагаем, что во внутренних точках объекта и ( x , t ) е H^2,1 ( ( 0,1 ) х ( 0, T ) ) п п С ( [ 0,1 ] х [ 0, T ] ) и g ( t ) , р ( t ) е С ^{2 +п} [ 0, T ] при всех T >  0 и ре (0,1). Также существуют постоянные С ₀, С 1 , С ₂ >  0 и Р ₀, Р 1 , Р ₂ >  0 такие, что | и ( x , t )| <  С ₀ e ^e 0 ⁽ x ⁺ t ) , |ф ( t )| < С 1 е ^e 1 t и |ф ( t )| < С ₂ e ^e 2 t выполнены при x е [0, Я ] и при всех t е [0, и ). При этом функции р ( t ) и ф ( t ) имеют конечное число экстремумов для любого t е [ 0, T ] при всех T >  0 , т. е. удовлетворяют условиям Дирихле.

Основываясь на характеристиках теплопереноса, математическая модель рассматриваемой задачи включает: уравнение теплопереноса ut = auxx, x е( 0, Я), t > 0,(1)

граничные условия, которые сформированы в соответствии с результатами измерений, полученных от датчиков, расположенных на поверхности и вблизи нее,

и(0,t) = p(t), и(x0,t) = g(t), t > 0,(2)

а также начальные условия и (x,0) = С, x e[0,Я].(3)

В данной задаче требуется найти граничное значение функции

и(Я,t) = ф(t) ,(4)

и затем, используя ф ( t ) , найти температурные значения вдоль всего линейного объекта. Задача (1)–(4) является обратной граничной задачей, существование и единственность решения которой обоснованы в [3, 7].

При решении поставленной задачи необходимо учитывать наличие отклонений результатов измерений от действительных значений. Представим эту ситуацию следующим образом. Вместо действительных значений g ₀ и (р₀ известны измеренные значения g _§ , (p _s и допустимый уровень отклонений 5 >  0 такой, что max {||фз —Ф₀||,|| g 5 — g 0I} < ^. Таким образом, требуется разработать метод определения температуры в контрольной точке и ₅ ( Я , t ) = ф₅ ( t ) по исходным данным р₅ , g ₅ , 5 и, основываясь на полученных результатах, определить температуру и ₅ ( x , t ) вдоль всего линейного объекта. Получить температурные значения с требуемой точностью можно за счет введения новых алгоритмов обработки результатов измерения, устойчивых относительно погрешности исходных данных.

Задача (1)–(4) относится к классу некорректных задач, когда малые отклонения в исходных данных приводят к значительным отклонениям в конечном результате [15].

В работе предложен следующий подход к построению вычислительной схемы определения температуры в контрольной точке. Сначала переходим к интегральной модели. С этой целью исходная задача с помощью преобразования Лапласа приводится к интегральному уравнению Вольтерра, которое характеризует прямую зависимость неизвестной функции ф ( t ) от исходных данных . Затем для результирующего интегрального уравнения разрабатывается численный метод решения и определяется приближенное значение ф₅ ( t ). Далее, основываясь на результатах, прогнозируется значение температурной функции и₅ (%, t) во внутренних точках объекта. Идея предложенного подхода к решению обратной граничной задачи является обобщением метода, представленного в работе [11].

Интегральная модель теплопереноса

В данной работе для получения интегрального уравнения, связывающего исходные данные и искомую функцию и(£,t) = v(t), предложен следующий подход. Сначала находим решение прямой задачи, полагая, что искомая функция ф(t) нам известна. Математическая модель прямой задачи имеет вид:

u_t = au_xx , x e ( 0, £ ) , t >  0,

и (0, t ) = ф( t), и (£, t ) = v( t), t > 0, и (x,0) = С, x е [0,£].

Исходя из характеристик процесса теплопереноса и следуя результатам, представленным в работе [14], применим прямое преобразование Лапласа к задаче (5)-(7). Функциям и ( x , t ) , ф ( t )

и ф ( t ) соответствуют изображения и ( x , p ) , ф ( p ) задачи (5)–(7) имеет вид:

pC

Uxx     и =     , aa

и (0,p) = ф(p), и (£,p) = v(p).

Решив задачу Коши (8)–(9), получаем, что:

и

v ( p ) . Операторное изображение прямой

и ( x , p ) = ф ( p )

V

( £ — x )

У

shjp £ a

+w ( p )

sh Jxx

V a

V

г

У

—

C

sh J^-i

N a

А

shjp £ a

—

p

V

( £ — x )    sh J p

Na

У

V

Основываясь на результатах, доказанных в [11], получаем:

shfe£ a

+

V

shfe£ a

x 11 У

У

sh J^-i

V a

V

( £ — x )

У

shjp £ a

£ — x 2

V>

^{£      n} n = 1

(—1)n . Глn(£ — x)

-------Sin I------------

n

£

p

₂₂ , n n a

p + ^2-

r

sh Jx-x

N a

V

sh,[p £ a

У

2 n

( — 1)      Гn nx

= + -> Sin I£ л n=1 n      V £

•

p n n a p +   2

.

+ - . (10) ^p

Ряды в правых частях (11) и (12) равномерно сходятся для всех x е ( 0, £ ) . Выполнив соответствующие преобразования в (10), получим, что решению задачи (5)–(7) соответствует следующее изображение:

и ( x , p ) = ф ( p )

£ - x

те

£

⁺1 ф ⁽ p ) E п

( — 1) ⁿ . Гп n ( £ — x )

-—— sin I — ----

n = 1

n

£

p +

p

n п a

+

£ ²

+v ( p )7 +-v ⁽ p ) £

£ п        n = 1

( — 1) ⁿ . Гп nx -—— sin I---

p

n

£

p +

n п a

+

£ ²

4 C +—Z п p _{n = 1}

2 n — 1

. f (2 n — 1) п % sin I ------------

£

•

p

p +

(2 n — 1)² п ² a

.

£ ²

Принимая во внимание, что функции ф(t) и ф(t) являются ограниченными и удовлетворя- ют условиям Дирихле, применим обратное преобразование Лапласа к обеим частям (13), используя теорему о свертке [15, 16], и получаем:

и ( x , t ) = ф ( t )

£ — x

£

2 d

1 -^x п dt

( — 1) ⁿ

2_2 n п a

. f п n ( £ — x ) ) t sin I ———- | e ^£

t

n = 1

n

£

J ф ( т ) e

22 n п a ^т

d т +

, x x 2 d

+V( t )- +-->

£ п dt

( — 1) n

2_2 n п a

. f пnx)    „2 t sin I —— | e £

t

n

£

J v ( t ) e

22 n п a —^т

d т +

4 C

+TX

n = 1

2 n — 1

. f (2 n — 1) л x ) - sin I  ---—— | e

£

— (2 n — 1) 2 п 2 a

£2

t

.

Введем следующие обозначения те

R 1 = X

( — 1) ⁿ . Гп n ( £ — x ) A --------sin I------------- | e

22 n п a

£ ²

t

t

n = 1

n

£

J ф ( т ) e

2 2 n п a

т

d т ,

те

R 2 = X

( — 1) n

22 n п a

■ f пnxA     „2 t sin I —— | e £

t

n = 1

n

£

J v ( t ) e

2 2 n п a

т

d т .

Исследуем сходимость полученных рядов. Из свойств функционалов в линейных нормиро- ванных пространствах [17] и функции ф(t) имеем:

t

2 2 n п a —-— т

t

22 n п a

J ф ( т ) e ^£    d т <  C 1 J

£ 2

⁺ Р 1 |т

e

d т

C 1 £ ²

( n ² п ² a + £ 2 P 1 )

22 n п a

£ ²

⁺ Р 1 |т

e

— 1

< C 1 £ 2 e

n п a „

—5- +в 1 |т

£2 J

( n ² п ² a + £ 2 Р 1 )

,

к

тогда справедлива следующая оценка

1 . f п n ( £ — x ) — sin I —------

n

<-

sin

n

£

— n п a

2 ^t e ^£

п n ( £ — x )

£

t

J ф ( т ) e

2 2 n п a

e £ 2

n л a ^т

-t C/e

•

d т

n п a

£ 2

<

+Р1 ^|т

<

0 31 t

C 1 £e

( n ² п ² a + £ 2 P 1 )    n ( n ² п ² a + £ 2 P 1 )

э 31 t

< C1£2e n Зп2 a

.

Отсюда, по теореме Вейерштрасса, следует абсолютная сходимость ряда R1. Рассуждая ана- логично и используя свойства функции ф( t), получим абсолютную сходимость ряда R2.

Используя свойства сходящихся рядов, раскрываем оператор d dt в (14) и получаем сле- дующее представление для функции и (x, t):

, x  2п —              (п n ( £ — x ))

и ( x , t ) = —— > (—1) ⁿ n sin —------ e

^£    n = 1             ^{У £ J}

2п —       , и+1   - Г п nx A

+—— > (—1) n n sin --- e

^£    n = 1               У ^{£ J}

2_2

n п — f tt

£ ²

и ²тт²л             n ²п² —

'^{n п —} t t         ---2— т

£2   |ф(т) e 1 d т + n п — т

4C      1    .

+--> ------sin п n : 1 2 n — 1

(2 n — IM A e

— (2 n — 1) ² п ² —t £ ²

£

.

Поскольку два ряда, входящие в формулу (15), являются расходящимися, то, используя идею, представленную в [9, 11], аппроксимируем точное решение задачи (5)–(7) конечным рядом:

N z x   2п — X2   . Г пnx A и (x, t) = —— > n sin --- e

^£    n = 1        ' ^{£ J}

n = 1

n п — f tt

£²      f

2 2 n п a

2 ^T

N ₁

2 п —         й+1 • Г п nx ।

+—— > ( — 1) n ^{+ 1} n Sin --- e

^£    n = 1               У ^{£ J}

n = 1

4 C ^{N 3}

⁺tE = 1

sin

2 n — 1

2_2 n п — f tt

£ ² f

22 n п a ^т

(2 n — 1) п x A e

— (2 n — 1) ² п ² —t £ ²

£

.

Так как функция u ( x ₀, t ) = g ( t ) известна, обозначив сеточный аналог этой функции через g_N ( t ), получим, что решение задачи (1)–(4) сводится к решению следующего интегрального уравнения:

2 п — x¹/ тхи+1

—E^{( —} 1) n ^{+ 1} n Sin

£    n = 1

t

-l

2 2

n^ ( t —т)

d ^т= g N ( t )

—

2п — E  .

n sin ²

^£    n = 1

t

2 2

— n п —

-( t — ^{т )}

d т —

4 C ^{N 3}    1

--> ------sin п ~12 n — 1

⁽² n ^{— 1) п} % 0 A e

£

— (2 n — 1) ² п ² —

.         £2

.

Введем функции К ( t , т ) и L ( t , т ) при всех t е [0, T ], согласно формулам:

N 1

K n ( t — т ) = -2- £ ( — 1) n ⁺ 1 n sin

n = 1

— n п —

У  5—⁽ t ^—т)

п nx. A     £ ²

0 e

£ J

,

— n п —

_T            2 п — ^N 2 . Г п nx. A £ ^{2 <-т}

L N ⁽ t ^{— т )} = -;r E n ^sin I      I ^e

^£ n = 1 ^{У £ J}

t

Обозначим A v = j K _n ( t — т)ф(т) d т , а

.

4 C ^{N 3}    1

hN(t) = gN(t)--E 2—; sin п n=12 n — 1

(2 n IM, A e

£

— (2 n — 1) ² п ² —

.        £2

tt

— j L_n ( t — т ) ф ( т ) d т .

Тогда эквивалентное представление интегрального уравнения (17) имеет следующий вид:

A _v= h N ( t ) .                                                                                           (18)

Из уравнения (18) при условии, что max {Ц ф д -Фо|| ,|| g s - g о| |} -8 для 5> 0, находим и ( £ , t ) = v ( t ) , а затем в области [0, £ ] х [0, T ] определяем значение функции u ( x , t ).

Вычислительная схема метода

В разделе предложен метод численного решения интегрального уравнения (18), основанный на регуляризующем подходе. Параметрами регуляризации являются шаг дискретизации по времени τ и величины N ₁ и N ₂. Основная особенность полученного уравнения Вольтерра заключается в том, что один из рядов в формуле (15) является знакопеременным, и это требует специального подхода к выбору величин N 1 и N 2 . В данном исследовании параметры регуляризации выбираются апостериорно.

Основные этапы численного метода решения интегрального уравнения заключаются в следующем:

• •    Выберем начальные значения s , N 1 и N 2 .

• •    Для вычисления интегралов введем равномерную сетку с узлами t i , где

t i = ( i - 1) т , т = T I s , 1 <  i <  s + 1.

• •    Аппроксимируем интегралы, входящие в уравнение (18), суммами, используя метод правых прямоугольников, и в результате получаем систему алгебраических уравнений.

• •    Решая данную систему уравнений, находим температурную функцию ^₅ ( t ) в контрольной точке А 2 .

• •    Итерационный процесс останавливаем, если выполнено условие

max |у5 (t) -V(t)| tе[0,T]                                  zn a

----------- ।----<8, где ее (0;0,1) .

max w ( t )

t e[0, T ]'        ¹

Вычислительный эксперимент

С целью проверки эффективности предложенного подхода к решению задачи теплопереноса, получения экспериментальных оценок погрешностей был проведен вычислительный эксперимент. В ходе эксперимента выполнен сравнительный анализ полученных решений с тестовыми значениями.

На первом этапе вычислительного эксперимента моделируются тестовые значения функции u (x, t) с помощью конечно-разностных уравнений. Для этого в области [0, £] х [0, T] введем рав- номерную сетку с узлами (xi,tj) , где xi = (i - 1) hx, ‘ tj=(j -1) ht,

<

h_x = £ I r , 1 <  i <  r +1;

h_t = T Im, 1 <  j <  m +1.

Далее моделируют исходные данные для обратной задачи, используя формулу (16), тогда g ( t i ) = u ( x 0 , t i ), где x 0 = k ■ £ , £ е (0,1).

Затем генерируются значения g5(ti) и ф5 (tj) по формулам gs (ti) = g (ti)+ ^5 (ti) Ф8 (tj) = Ф(tj) + 05 (tj), где ст5(ti) и 05 (tj) являются значениями случайных величин, равномерно распределенных на отрезке [-5,5].

На втором этапе вычислительного эксперимента находят решение ф₅ ( t ) интегрального уравнения (18) с помощью предложенного численного метода. Функция ^ 5 ( t ) соответствует температурным значениям в контрольной точке.

На третьем этапе оценивают температурные погрешности с помощью функции А ( t ) и величин A_v , e_v , определяемых по формулам:

^{А (} t ) = |V s ⁽ t ) ^-V ⁽ t )|, A_v

A,„ = max A( t ), 8... =-----------7.

^v    t е [0, T ] ^{v v} max v ( t )

t е [0, T ]'

На следующем этапе эксперимента находят решение u ₅ ( x , t ) задачи теплопереноса (1)-(4), используя полученную функцию ^₅ ( t ). Функция u ₅ ( x , t ) соответствует тепловому полю линейного объекта.

Вычислительный эксперимент проводился в области [0, £ ] х [0, T ] при £ = 1 и T = 1, начальная температура объекта u ( x ,0 ) = 0, x е (0, £ ), коэффициент температуропроводности a = 1.

Результаты вычислительного эксперимента для некоторых тестовых функций представлены в данной работе. В качестве тестовых использовались следующие типы функций:

• 1)    температурная функция на поверхности объекта задана формулой ф 1 ( t ) = 25( e ² t - 1), а в контрольной точке температуру определяет функция v 1 ( t ) = 100 te ^0,8 t ;

• 2)    на поверхности тела задана температурная функция ф ₂( t ) = 1000 t ( e - t - e ^{- 2} ), а в контрольной точке температуру определяет функция ^ ₂( t ) = 500 te - t .

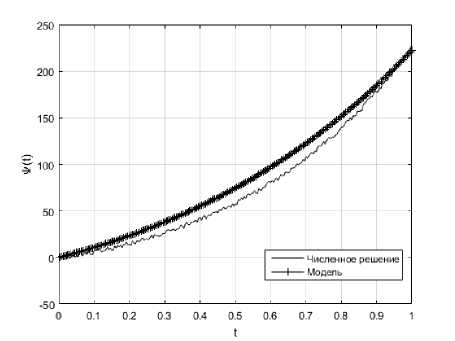
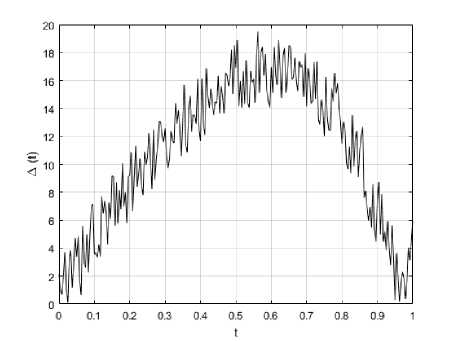
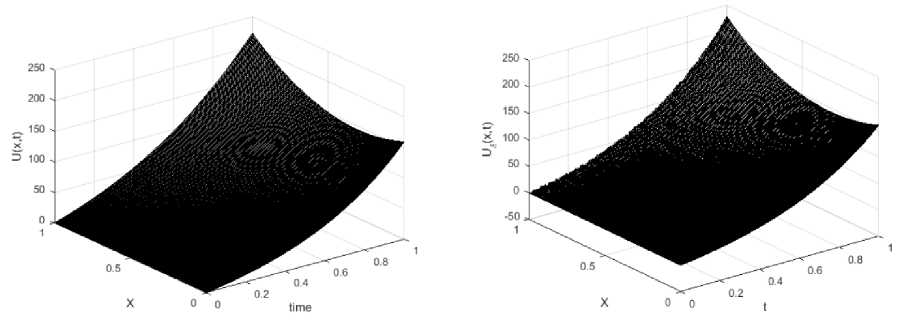
На рис. 2а и 4а представлены графики тестовых функций ^ ( t ) и графики приближенных численных решений ^₅ ( t ) задачи (1)-(4). На рис. 2б и 4б представлены графики функций температурных погрешностей. На рис. 3а и 5а построены поверхности u ( x , t ) , соответствующие решениям прямой задачи (5)-(7), а на рис. 3б и 5б - графики поверхностей u ₅ ( x , t ) .

а)

Рис. 2: а – результаты вычислительного эксперимента для тестовых функций

Ф 1 ( t ) = 25 ( e ² t - 1 ), ф 1 ( t ) = 100 te ^{0 , 8} t ; б - график функции температурной погрешности Д ( t )

б)

а)                                                            б)

Рис. 3: а – график функции u ( x , t ) , соответствующей решению прямой задачи для тестовых функций ϕ ₁ ( t ) = 25 ( e ^{2 t} - 1 ), ψ ₁ ( t ) = 100 te ^{0 , 8 t} ; б – результаты моделирования температуры во всех точках линейного объекта для приближенного решения ψ _δ ( t )

а)                                                           б)

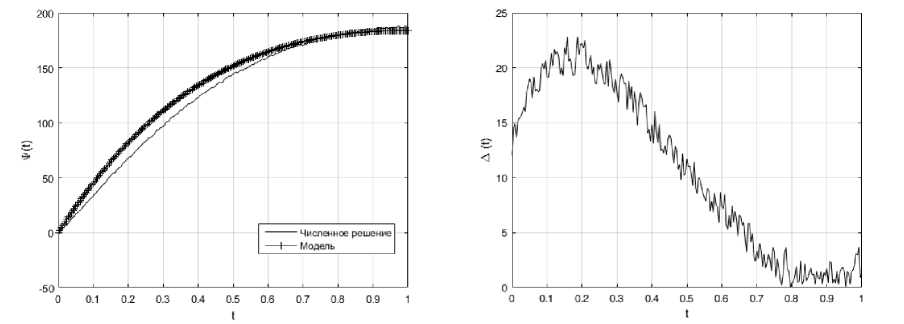
Рис. 4: а – результаты вычислительного эксперимента для тестовых функций ϕ ₂ ( t ) = 1000 t ( e ^{- t} - e ^{- 2} ), ψ ₂ ( t ) = 500 te ^{- t} ; б – график функции температурной погрешности Δ ( t )

а)

б)

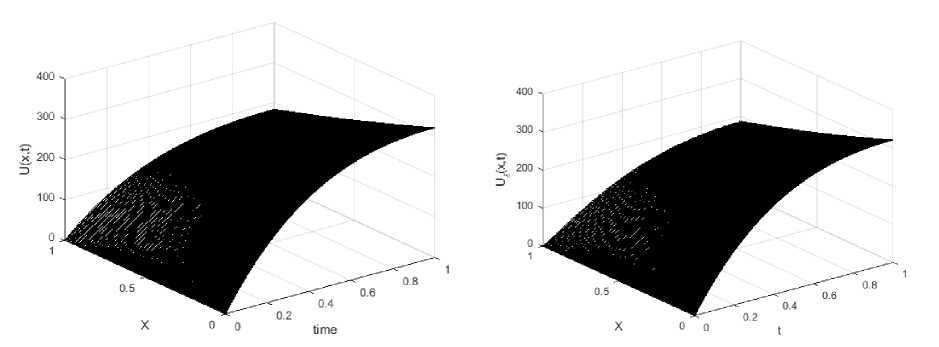
Рис. 5: а – график функции u(x, t) , соответствующей решению прямой задачи для тестовых функций ϕ2(t) = 1000t(e-t -e-2), ψ2(t) = 500te-t ; б – результаты моделирования температуры во всех точках линейного объекта для приближенного решения ψδ (t)

В таблице представлены экспериментальные значения абсолютной погрешности Δ_ψ и относительной погрешности ε_ψ , полученные при различных значениях параметров регуляризации и δ = 0,5.

Экспериментальные оценки погрешностей

Тестовые функции	Значения параметров		Погрешности
	h	N i	Абсолютная Δψ	Относительная εψ
ϕ 1( t ) и ψ 1( t )	1/500	N 1 = 27, N 2 = 26	85,8134	1,8668
		N 1 = 57, N 2 = 56	86,1302	1,8737
		N 1 = 87, N 2 = 86	21,7133	0,4724
	1/200	N 1 = 27, N 2 = 26	4,2834	0,0932
		N 1 = 57, N 2 = 56	3,0929	0,0673
		N 1 = 87, N 2 = 86	2,8045	0,0610
ϕ 2( t ) и ψ 2( t )	1/500	N 1 = 27, N 2 = 26	2,4359∙1011	–
		N 1 = 57, N 2 = 56	2,8864∙1010	–
		N 1 = 87, N 2 = 86	7,6024∙109	–
	1/200	N 1 = 27, N 2 = 26	2,8892	0,0625
		N 1 = 57, N 2 = 56	2,8045	0,0607
		N 1 = 87, N 2 = 86	2,7901	0,0604

Результаты вычислительного эксперимента свидетельствуют о том, что предложенный подход к решению задачи линейного теплопереноса позволяет получать решения с достаточной точностью.

Заключение

В данной работе рассмотрена задача определения температуры внутри объекта, который подвергается внешнему тепловому воздействию. Основываясь на характеристиках процесса, задача измерения температуры имеет вид задачи теплопереноса в линейном объекте. Математическая модель представлена уравнением теплопроводности с известными на границе и вблизи нее температурными функциями. С помощью применения прямого и обратного преобразования Лапласа эта задача сведена к интегральному уравнению, характеризующему прямую зависимость неизвестной температурной функции от исходных данных. Численный метод решения полученного интегрального уравнения основан на применении многопараметрического регуляризующего подхода, а для нахождения температурных значений во внутренних точках линейного объекта применялись конечно-разностные уравнения.

В ходе вычислительного эксперимента найдены экспериментальные оценки погрешностей полученных решений. Результаты эксперимента свидетельствуют о достаточной точности предложенного подхода к определению температуры во внутренних точках объекта, недоступных для непосредственного теплового контроля.

Работа выполнялась при финансовой поддержке Министерства образования и науки Российской Федерации в рамках базовой части Государственного задания «Разработка, исследование и реализация алгоритмов обработки данных динамических измерений пространственно-распределенных объектов», техническое задание 8.9692.2017/8.9 от 17.02.2017.