Интегральное уравнение для численного решения стационарных квантово-механических задач
Автор: Князев Сергей Юрьевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 3 (86) т.16, 2016 года.
Бесплатный доступ
Целью работы является описание метода численного решения стационарного уравнения Шредингера, основанного на использовании интегрального уравнения, тождественного уравнению Шредингера. По своей структуре это интегральное уравнение близко к уравнению Фредгольма второго рода и допускает получение численного решения задачи. Рассматриваемый метод позволяет находить собственные значения энергии и собственные решения для квантово-механических задач различной размерности. Приведены результаты тестирования метода при решении задачи для одномерного и двумерного квантового осциллятора. Найденные численным методом значения собственных энергий и собственных функций осциллятора сравнивались с известными аналитическими решениями, затем оценивалась погрешность результата. Наибольшая точность решения получена для первых энергетических уровней. Погрешность численного решения возрастает с номером собственного значения энергии. Для последующего энергетического уровня погрешность увеличивается почти на порядок. Для четвертого энергетического уровня при разбиении области интегрирования на 500 элементов погрешность решения для собственных функций не превосходит 2%. Если энергетический уровень является вырожденным, то существует возможность получения всех собственных функций, соответствующих данному уровню. Для этого используются различные вспомогательные функции, симметрия которых согласуется с симметрией собственной функции.
Уравнение шредингера, собственные значения, собственные функции, численное решение, фундаментальные решения
Короткий адрес: https://sciup.org/14250232
IDR: 14250232 | УДК: 519.632;539.182 | DOI: 10.12737/20217
Текст научной статьи Интегральное уравнение для численного решения стационарных квантово-механических задач
Введение. Фундаментальное значение при решении квантовых механических задач описывается уравнением Шредингера [1]. Аналитические решения этого уравнения могут быть получены лишь для весьма ограниченного круга задач, преимущественно одномерных. Поэтому разработано множество приближенных методов решения уравнения Шредингера, как аналитических, с использованием теории возмущения [2–4], так и прямых численных методов. Несмотря на широкий спектр имеющихся численных методов решения уравнения Шредингера, таких, например, как метод Нумерова [5], метод диагонализации [6–7], спектральный метод [7], и других численных методов [8–12], проблема эффективных способов нахождения собственных энергий и собственных функций для основного уравнения квантовой механики, особенно при решении многомерных задач, продолжает оставаться актуальной. Ниже предложена методика решения уравнения Шредингера, основанная на приведении его к интегральному уравнению с последующим численным решением.
Интегральное уравнение Шредингера. Пусть частица массой т , совершает финитное движение в силовом поле V ( r ) . Запишем стационарное уравнение Шредингера в виде
АТ + 2mE Т = ^m-V ( r ) Т . (1)
Необходимо, решая уравнение (1), найти собственные значения энергии Е и соответствующие им собственные функции, волновые функции частицы Т ( r ) .
Перейдем от однородного уравнения Шредингера к неоднородному уравнению, введя новую искомую функцию
U ( r ) = Т ( r ) - u 0 ( r ) , (2)
где заданная вспомогательная функция u 0( r ), как будет показано ниже, может определять некоторые особенности решения. Теперь уравнение Шредингера запишем как
A U + X U = v ( r ) U - ( A + X + v ) u 0, (3)
где X = -mE , v ( r ) = 2 mV ( r ) .
2 2 V 7 2 2 V 7
Правую часть в (3) можно рассматривать как плотность некоторого фиктивного заряда р ( r ) , создающего поле
U ( r ) , удовлетворяющее неоднородному уравнению Гельмгольца:
AU + ХU = р(r), где
р ( r ) = v ( r ) U ( r ) - ( A + X + v ( r ) ) u 0 ( r ) . (4)
Частное решение этого уравнения можно представить в виде
U ( r ) =Jp ( R ) g ( r , R ) d Q r . (5)
Q
Здесь g ( r , R ) — фундаментальное решение уравнения Гельмгольца, которое можно рассматривать как поле, созданное в точке r единичным положительным точечным зарядом, расположенным в точке R . Конкретный вид фундаментальных решений для уравнений Гельмгольца различных размерностей хорошо известен [13].
Физически разумно предположить, что область интегрирования Ω в соотношении (5) близка, но несколько больше классически доступной для частицы области, границы которой определяются уравнением
V ( r ) = E . (6)
В общем случае поле, соответствующее уравнению Гельмгольца, суммируется из поля, соответствующего частному решению (5), и поля, созданного внешними «зарядами», расположенными за пределами области Ω, или на ее границе. Здесь также, исходя из физических соображений, можно полагать, что источники реального физического поля, поля волновой функции частицы, находятся в пределах области Ω и, таким образом, основная составляющая волновой функции U ( r ) удовлетворяет уравнению (5). Теперь, после подстановки в (5) плотности заряда (4), для искомой функции U ( r ) получается интегральное уравнение
U ( r ) -J U ( R ) v ( R ) g ( r , R ) d Q R =-J ( A + X + v ( R ) )u o ( R ) g ( r , R ) d Q r . (7)
Q Q
Уравнение (7) есть интегральное уравнение Шредингера, являющееся следствием уравнения (3). Можно показать, что, наоборот, уравнение Шредингера (3) является следствием интегрального уравнения (7).
Решение тестовой задачи для одномерного осциллятора. Уравнение (7) можно решать численно. Наиболее простой случай — решение одномерных задач. В этом случае, с помощью уравнения (6) находится отрезок [ a, b ]= Ω, в пределах которого потенциальная энергия частицы не превосходит ее полной энергии Е . На отрезке [ a, b ] равномерно располагаются N узлов x i (1 < i < N ). Значение поля в этих точках обозначим U i . Интегралы в уравнении (7) заменяем их приближенными значениями, используя какой-либо численный метод интегрирования, например, метод прямоугольников. В результате для N искомых величин U i получается система N линейных алгебраических уравнений вида:
N
Z a ij U j = bi . (8)
j = 1
При вычислении коэффициентов системы (8) при положительных λ используется фундаментальное решение одномерного уравнения Гельмгольца [14]
g (x, X ) =
sin (Vx | x - X |) 2 ^
Описанный здесь метод численного решения уравнения Шредингера тестировался на примере решения задачи для квантового гармонического осциллятора. В этом случае область решения представляла собой отрезок длиной
L = 2
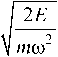
где to — частота осциллятора. Чтобы зафиксировать резкое убывание волновой функции за пределами классически
2E допустимой области отрезок несколько увеличивают, полагая его, например, равным L = 3 ---- . Затем задается
тю2
начальное значение энергии частицы, например, Е0=0, и шаг варьирования энергии бе. Желательно, чтобы этот шаг был много меньше расстояния АЕ между ближайшими собственными значениями энергии, бе<< ДЕ. Для каждого значения энергии E=E0+nбе последовательно, при n=0, 1, 2,... решается система (8) и находятся значения волновой функции в крайних точках области решения. Те значения энергии, для которых величина e = |^J + |^N | имеет наименьшее, близкое к нулю значение, возможно, являются собственными значениями решаемой задач. Для уточнения этих значений можно сузить область поиска и уменьшить шаг варьирования энергии бе. Назовем параметр K = 1/e = 1/(1^,1 + |ТN |), обратный к величине e, критерием задачи на собственные значения энергии. На рис. 1
E 1
представлен график зависимости критерия задачи K от приведенной энергии ц =---, который в процессе ю 2
вычислений менялся в пределах от 0 до 10 с шагом бц = 0,1. Собственным значениям энергии в этом случае должны соответствовать максимальные значения критерия задачи K . Число узлов N в области решения задачи устанавливалось равным N =100.
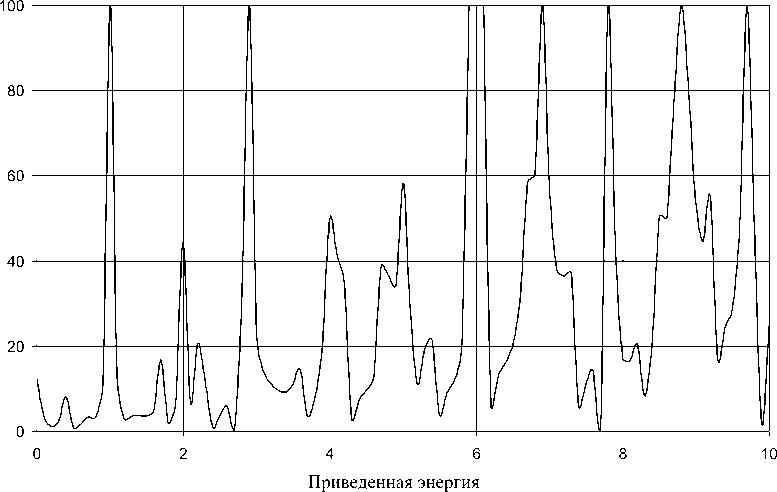
Рис. 1. Зависимость критерия задачи на собственные значения энергии от приведенной энергии одномерного квантового осциллятора
На рис. 1 наблюдаются четкие максимумы при целочисленных значениях ц от 1 до 7. При ц=0 максимум выражен достаточно слабо, а при ц >7 положения максимумов несколько смещаются в область меньших значений и наблюдаются уже при ц =7,9; 8,9; 9,8. Это, видимо, связано с тем, что с ростом номера собственной энергии количество осцилляций волновой функции в области решения возрастает. Это приводит к возрастанию погрешности численного решения для собственной функции и, соответственно, к увеличению погрешности для критерия K . Эта проблема устраняется путем увеличения количества узлов N и уменьшения шага варьирования энергии бц .
Численное решение уравнения (7) оказывается весьма чувствительно к значению параметра ц, который определяет значение энергии Е. На рис. 2 представлены графики зависимости значений волновой функции ψ от приведенной координаты частицы x/L. Толстой сплошной кривой представлена собственная функция, соответствующая ц=2. График собственной функции, рассчитанный при количестве узлов N=100, в этом случае сливается с теоретической зависимостью, рассчитанной с использованием полиномов Эрмита. Пунктирная кривая на рис. 2 получена при ц=2,1.
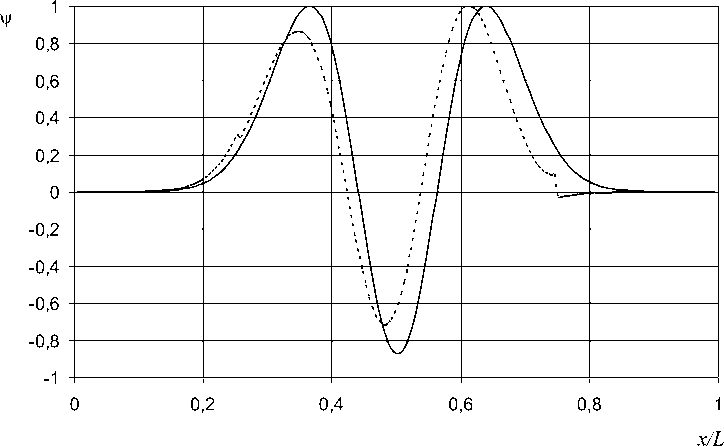
Рис. 2. Зависимость значений волновой функции у от приведенной координаты частицы x/L
Как видно из рис. 2, на графике, полученном при ц=2,1, т. е. при значении энергии не равном собственному значению, кроме некоторого количественного различия с графиком собственной функции наблюдаются изломы, скачки. Наличие таких изломов, скачков является одним из признаков отклонения от собственного значения энергии.
Основным параметром, определяющим точность численного решения, является, естественно, количество узлов N в области решения задачи. В качестве меры погрешности при вычислении собственных функций использовалась величина s = max|vi -Ф(x)|, (10)
где ф ( Xi ) — значение аналитического решения задачи в точке с координатой x i . При вычислении погрешности численного решения предварительно производилась нормировка собственных функций путем их деления на максимальное по абсолютной величине значение этих функции в области решения задачи. На рис. 3 представлены графики зависимостей погрешностей численного решения от количества узлов N , полученные для трех собственных функций: с ц =0 (сплошная толстая кривая на рис. 3); ц =1 (тонкая сплошная кривая на рис.3); ц =2 (пунктирная кривая на рис. 3).
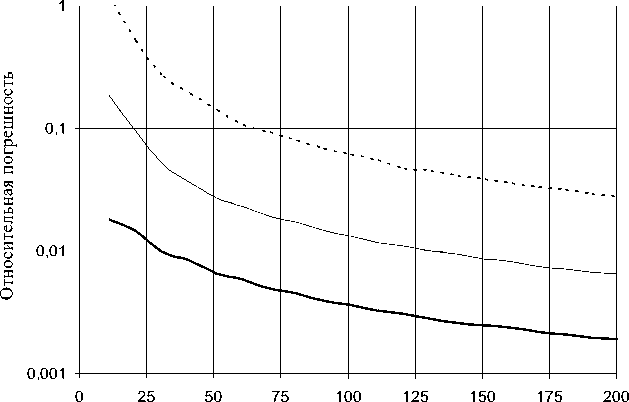
Количество узлов N
Рис. 3. Графики зависимостей погрешностей численного решения от количества узлов N . Сплошная толстая линия соответствует ^ =0; тонкая сплошная линия соответствует ^ =1; пунктирная линия соответствует ^ =2
Из рис. 3 очевидно, что погрешность численного решения для собственных функций убывает с ростом N, причем с увеличением N быстрота убывания погрешности уменьшается. Одновременно погрешность численного решения возрастает с номером собственного значения энергии: погрешность для последующего энергетического уровня увеличивается почти на порядок. Увеличивая число N , можно обеспечить приемлемую точность вычислений. Например, для четвертого энергетического уровня с ц =4 при N =500 погрешность решения не превосходит 2%. При этом следует отметить, что во всех случаях средняя или среднеквадратичная погрешность оказывается значительно меньше.
Приведенные выше результаты получены при использовании вспомогательной функции u0 (r ) = 1 + х. Если использовать вспомогательную функцию u0 (r) = 1, то при численном решении уравнения (7) правильные значения собственных энергий и собственных функций получаются только для четных значений μ. Напротив, при использовании нечетных ц правильные значения собственных энергий и собственных функций получаются при нечетных ц. Это обусловлено свойствами симметрии силового поля V (r) и фундаментальных решений, а также структурой уравнения (7). Используемая здесь функция u0 (r ) = 1 + х есть сумма четной и нечетной функций, что позволило получить решения, обладающие различной симметрией.
Если при разработке алгоритма численного решения задачи учитывать определенные свойства симметрии волновых функций, можно оптимизировать компьютерную модель, сократить объем вычислений и повысить их точность.
Решение тестовой задачи для двумерного осциллятора. Основным достоинством описываемого здесь метода решения уравнения Шредингера является возможность применения его, без существенного усложнения, при решении многомерных задач. Основная трудность решения связана с резким увеличением количества линейных уравнений типа (8) при увеличении размерности задачи. Ниже приводятся основные результаты решения тестовой двумерной задачи для двумерного изотропного квантового осциллятора.
2 m
При вычислении коэффициентов системы (8) при положительных значениях Х = —— E используется фундаментальное решение двумерного уравнения Гельмгольца, выражаемое через функции Ханкеля нулевого порядка первого вида [13]:
g ( r , R ) = iH 01) (V ^ r - R I ) .
Энергию осциллятора представим в виде E=Ex+Ey, где Ex и Ey — составляющие энергии, обусловленные движением вдоль осей Х или Y соответственно. Область решения представляется в виде прямоугольника со сторонами Lx = 3,
2 E 2 E y
—x- и Ly = 3.1---- . Разумеется, размеры области решения могут несколько отличаться от этих
m щ2 у m ю2
значений. Однако значительные отклонения этих размеров от рекомендуемых приводит к возрастанию погрешности вычислений, что может затруднить анализ результатов при определении собственных значений энергии.
Алгоритм решения задачи на поиск собственных значений энергии повторяет описанный выше алгоритм для одномерного случая. Задается начальное значение энергии частицы, например, Е0=0, и шаг варьирования энергии бе. Для каждого значения энергии E=E0+nбе последовательно, при n=0, 1, 2,... решается система (8) и находятся значения волновой функции в крайних точках области решения. Те значения энергии, для которых величина e = ^|Т^| (здесь k суммирование производится по значениям волновой функции |Тk| в граничных узлах области решения) имеет наименьшее, близкое к нулю значение, возможно, являются собственными значениями решаемой задач.
На рис. 4 представлен график зависимости критерия задачи на собственные значения энергии
K = 1 / e = 1 / ^ 1^ k от приведенной энергии ц = — - 1, который в процессе вычислений менялся в пределах от -0,5 до k го
-
2,5 с шагом бц = 0,1. Собственным значениям энергии в этом случае должны соответствовать максимальные
критерии задачи K . Число узлов N в области решения задачи устанавливалось равным N = 24 х 24 = 576 . Вычисления проводились при u о ( r ) = 1 + х .
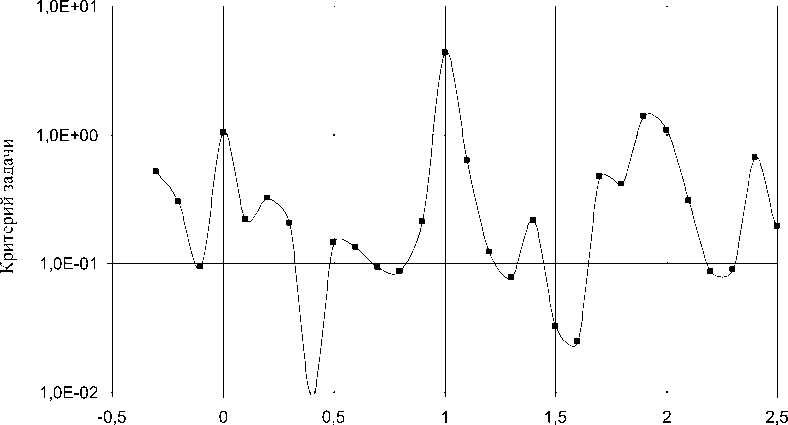
Приведенная энергия
Рис. 4. Зависимость критерия задачи на собственные значения энергии от приведенной энергии двумерного квантового осциллятора
На рис. 4 наблюдаются четкие максимумы при значениях μ=0 и μ=1. При μ≈2 максимум несколько смещен в область меньших значений, к μ=1,9. Эти результаты согласуются с точными собственными значениями энергии двумерного осциллятора E m = hto ( ^ + 1 ) , Ц = 0,1,2,... Однако следует обратить внимание также на наличие нескольких второстепенных локальных максимумов при значениях μ, не совпадающих с теоретически ожидаемыми результатами. Увеличение числа узлов с N = 576 до N = 30 х 30 = 900 несколько улучшает результат, однако второстепенные максимумы сохраняются, что может приводить к ошибкам при идентификации собственных значений энергии.
Определенные трудности возникают также при учете вырожденности энергетических уровней. Например, второму энергетическому уровню с μ=1 можно поставить в соответствие две собственных функции. Одна из них симметрична относительно оси Х и антисимметрична относительно оси Y , а другая — наоборот, симметрична относительно оси Y и антисимметрична относительно оси X . Для вычисления собственных функций в этих двух случаях описанным выше способом желательно использовать различные области решения (с разными соотношениями сторон) и различные вспомогательные функции и 0 ( r ) . В первом случае это может быть и 0 ( r ) = 1 + у , а во втором — и 0 ( r ) = 1 + х.
Заключение. Проведенный анализ показывает перспективность предложенного численного метода решения квантово-механических задач различной размерности. Разработанный способ решения уравнения Шредингера может быть использован при решении различного типа эллиптических уравнений неканонической формы. Дополнительные возможности возникают также при использовании в интегральном уравнении, подобном уравнению (7), фундаментальных решений, предварительно найденных численным методом. Это позволяет, в частности, расширить круг решаемых задач путем использования метода точечных источников поля [15–20].
Список литературы Интегральное уравнение для численного решения стационарных квантово-механических задач
- Ландау, Л. Д. Квантовая механика. Нерелятивистская теория/Л. Д. Ландау, Е. М. Лифшиц. -Москва: Гос. изд-во физ.-мат. лит., Наука, 1963. -703 с.
- Kesarwani, R. N. Eigenvalues of an anharmonic oscillators/R. N. Kesarwani, Y. P. Varshni//J. Math. Phys. -1981. -Vol. 22. -№ 9. -P. 1983-1989.
- Ульянов, В. В. Интегральные методы в квантовой механике/В. В. Ульянов. -Харьков: Вища школа. Изд-во при Харьк. ун-те, 1982. -160 с.
- Bender, С. М. Anharmonic oscillator. II. A study of perturbation theory in large order/С. М. Bender, Т. Т. Wu//Phys. Rev. -1973. -Vol. 7. -№ 6. -P. 1620-1636.
- Killingbeck, J. P. Microcomputer Quantum Mechanics/J. P. Killingbeck. -Adam Hiller, 1983. -p. 380.
- Banerjee, К. The anharmonic oscillator/К. Banerjee, S. P. Bhatnagar, V. Choudhry, S. S. Kanwal//Proc. R. Soc. A, 1978. -Vol. 360. -P.575-586.
- Черкасский, В. А. Численное решение уравнения Шредингера: метод диагонализации и спектральный метод/В. А. Черкасский//Вiсник Харкiвського нацiонального унiверситету. -2010. -№ 926. -С. 204-211.
- Dineykhan, M. The Schroedinger equation for bound state systems in the oscillator representation/М. Dineykhan, G. V. Efimov//Repots of Math. Phys. -1995. -V.6. -№ 2/3. -P. 287-308.
- Abrashkevich, A. G. FESSDE, a program for the finite-element solution of the coupled-channel Schroedinger equation using high-order accuracy approximations/A. G. Abrashkevich, D. G. Abrashkevich, M. S. Kaschiev, I. V. Puzynin//Соmр. Phys. Commun. -1995. -Vol. 85 -P. 6574.
- Jafarpour, М. Calculation of energy eigenvalues for the quantum anharmonic oscillator with a polynomial potential/М. Jafarpour, D. Afshar//J. Phys. A: Math. Gen. -2002. -Vol. 35 -P. 87-92.
- Квитко, Г. В. Численное решение уравнения Шрёдингера с полиномиальными потенциалами/Г. В. Квитко, Э. Л. Кузин, Д. В. Шоть//Вестник Балт. муницип. ин-та им. И. Канта. -2011. -Вып. 5. -С.115-119.
- Лукьяненко, А. Н. Символьно-численное решение двумерного уравнения Шрёдингера с двухъямным потенциалом/А. Н. Лукьяненко, Н. А. Чеканов//Университет им. В.И. Вернадского. -2008. -№ 3(13). -Т. 2. -С. 43-50.
- Полянин, А. Д. Справочник по линейным уравнениям математической физики. -Москва: Физматлит, 2001. -576 с.
- Владимиров, B. C. Уравнения математической физики/В. С. Владимиров, В. В. Жаринов. -Москва: Физматлит, 2004. -400 с.
- Fairweather, G. The method of fundamental solutions for problems in potential theory/G. Fairweather, R. L. Johnston//Treatment of Integral Equations by Numerical Methods/eds. C. T. H. Baker, G. F. Miller. -London: Academic Press, 1982. -P. 349-359.
- Князев, С. Ю. Численное решение уравнений Пуассона и Гельмгольца с помощью метода точечных источников/С. Ю. Князев//Изв. вузов. Электромеханика. -2007. -№ 2. -С. 77-78.
- Князев, С. Ю. Численное решение краевых задач для неоднородных уравнений Гельмгольца методом точечных источников поля/С. Ю. Князев, Е. Е. Щербакова, А. Н. Заиченко//Известия высших учебных заведений. Электромеханика. -2014. -№ 4. -С. 14-19.
- Князев, С. Ю. Решение задач тепло-и массопереноса с помощью метода точечных источников поля/С. Ю. Князев, Е. Е. Щербакова//Известия высших учебных заведений. Северо-Кавказский регион. Серия: Технические науки. -2006. -№ 4. -С. 43-47.
- Князев, С. Ю. Моделирование полей упругих деформаций с применением метода точечных источников/С. Ю. Князев, В. Н. Пустовойт, Е. Е. Щербакова//Вестник Дон. гос. техн. ун-та. -2015. -Т. 15. № 1 (80). -С. 29-38.
- Князев, С. Ю. Моделирование трехмерных полей упругих деформаций с помощью метода точечных источников/С. Ю. Князев, В. Н. Пустовойт, Е. Е. Щербакова, А. А. Щербаков//Вестник Дон. гос. техн. ун-та. -2015. -Т. 15. № 4 (83). -С. 13-23.


